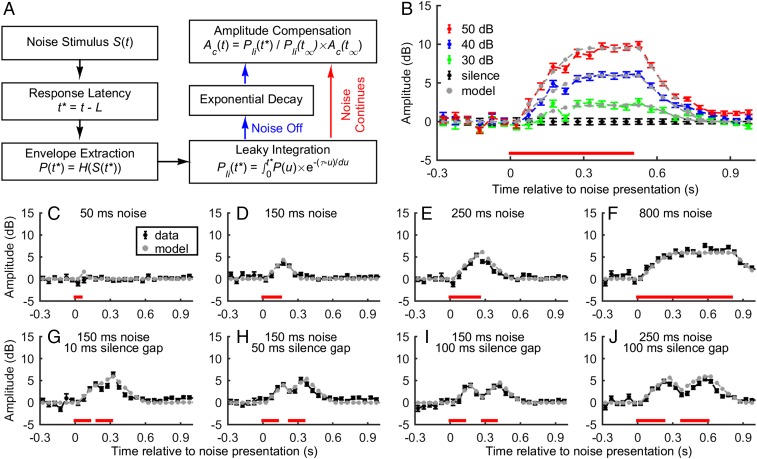
Fig. 4.

A computational model for the Lombard effect. (A) The model takes the white noise as the input, followed by envelope extraction, leaky integration, and scaling. There are three free parameters: the response latency (ms), time constant (ms), and maximum compensation (dB). (B) Data from the 500-ms continuous noise conditions were used to find the optimal combination of the three model parameters through minimizing the sum of squared errors. The corresponding model predictions are colored in gray. (C–J) A comparison of the model prediction, based on the three parameters optimized from the 40-dB SPL noise condition (267 ms of time constant, 30 ms of response latency, and 5.9 dB of maximum compensation), and the data. The model precisely predicts the time course of the call amplitude for all conditions. For B–J, the red bar at the bottom shows the time course of noise presentation.