Figure 2.

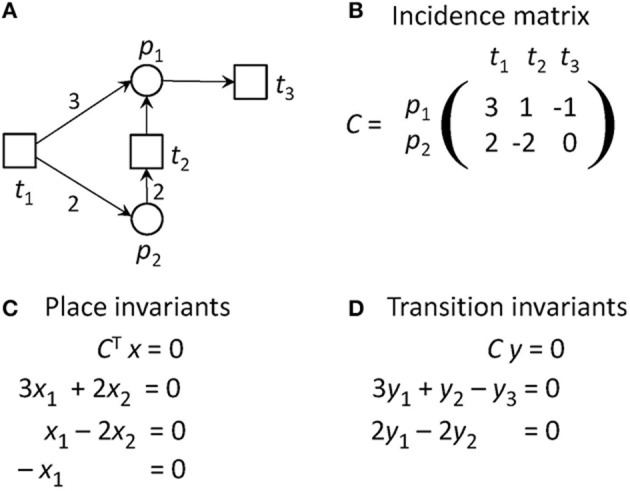
The definitions of invariants of the PN in Figure 1A. (A) The PN in Figure 1A. (B) The incidence matrix, C, of the PN. The matrix indicates how many tokens are removed from or consumed on the places when a transition fires. For example, if t₁ fires, three tokens will be produces on p₁ and two tokens on p₂. (C) The equation system to compute the place invariants. (D) The equation system to compute the transition invariants. The PN has no place invariants, but is covered by transition invariants. It has one TI = {t₁, t₂, 4 t₃}, meaning that t₁ and t₂ have to fire each once and t₃ four times, before the original state will be reached again.