Abstract.
An x-ray energy spectrum plays an essential role in computed tomography (CT) imaging and related tasks. Because of the high photon flux of clinical CT scanners, most of the spectrum estimation methods are indirect and usually suffer from various limitations. In this study, we aim to provide a segmentation-free, indirect transmission measurement–based energy spectrum estimation method using dual-energy material decomposition. The general principle of this method is to minimize the quadratic error between the polychromatic forward projection and the raw projection to calibrate a set of unknown weights, which are used to express the unknown spectrum together with a set of model spectra. The polychromatic forward projection is performed using material-specific images, which are obtained using dual-energy material decomposition. The algorithm was evaluated using numerical simulations, experimental phantom data, and realistic patient data. The results show that the estimated spectrum matches the reference spectrum quite well and the method is robust. Extensive studies suggest that the method provides an accurate estimate of the CT spectrum without dedicated physical phantom and prolonged workflow. This paper may be attractive for CT dose calculation, artifacts reduction, polychromatic image reconstruction, and other spectrum-involved CT applications.
Keywords: computed tomography, dual-energy computed tomography, material decomposition, spectrum estimation, Monte Carlo, least square, optimization, cone-beam computed tomography
1. Introduction
X-ray computed tomography (CT) uses polychromatic x-ray photons to scan objects from different view angles. The energy spectrum of the x-ray photons is highly correlated to the reconstructed image value, which is directly related to the application of CT scanners. Essentially, the spectrum plays a very important role in dose calculation,1 polychromatic image reconstruction,2 artifacts reduction,3,4 spectral CT,5–7 and high-contrast CT imaging.8 To obtain the spectrum, a natural solution is to directly measure the energy of x-ray photons using energy-resolved detectors. However, to acquire high-quality diagnostic CT images, the x-ray photons flux of a CT scanner in clinical application is usually quite high (can exceed 9). For comparison, the count rate of a typical energy-resolved detector is only ;10 thus, it is not easy to directly measure the energy spectrum of the CT scanner using the energy-resolved detectors as the detector pile-up effect limits the maximum count rate. Instead, spectrum calibration often employs indirect methods, including Compton-scattering measurement,11–13 Monte Carlo (MC) simulation,14–18 empirical or semiempirical physical models,19–22 and transmission measurements.23–28
The Compton-scattering method aims to significantly reduce the incident photon flux with a factor of to . With this method, the scattered spectrum can be measured using a high-purity germanium detector29,30 or a cadmium telluride detector.31,32 The incident spectrum is then reconstructed using the scattered spectrum and the corresponding scattering angle. However, the accuracy of the spectrum estimated using this method may suffer from the absorption in the scatterer and the limited absorption efficiency of the detector; thus, careful system calibration is needed before yielding the final spectrum.
MC simulation can be easily used to generate the spectrum of an x-ray tube when its specifications (such as target angle and target material) are well known. In this case, the x-ray tube is modeled using an MC toolkit (such as Geant433) with its specifications exactly matched with that in the realistic application. Monochromatic electrons are emitted from an electron gun and accelerated to hit the target. Both bremsstrahlung and characteristic x-ray photons are generated and filtered by the inherent filtration material. As most of the MC toolkits provide comprehensive physics modeling and are well validated,34–36 spectrum generated in this way can precisely match the real spectrum. However, the x-ray tubes are usually proprietary, and it is difficult to obtain the exact tube specifications, especially for the tube filtration, which is very important for spectrum simulation.
Spectral modeling calculates the x-ray spectrum using mathematical models. These models are based on physical processes, including bremsstrahlung and characteristic x-ray production. To yield a more accurate spectrum, a refined model that accounts for self-absorption of the x-rays within the target was also introduced. Nowadays, the popular spectral modeling methods usually adopt an empirical or a semiempirical approach that fits a parameterized model based on previously measured or simulated spectra.19,20,22
Transmission measurement is another methodology for spectrum estimation using projection data of a calibration phantom.37–39 The rationale of this method is based on the fact that a harder spectrum yields a less attenuated projection, whereas a softer spectrum yields a more attenuated projection. The method formulates the polychromatic forward projection equation as a discrete linear system in which the energy bins of the spectrum are described as unknown variables40 and then solves the linear system to obtain each bin content of the spectrum.
The accuracy of the aforementioned methods usually suffers from various limitations. For example, low-energy tailing yielded by the hole-trapping effect and environmental conditions (such as low temperature requirement) may affect the spectrum measured using energy-resolved detectors.41 Attenuation and scattering (e.g., Rayleigh and multiple Compton) in the material of the scatterer of the Compton-scattering measurement need to be carefully considered.32 Transmission measurements based on step or wedge phantom require dedicated hardware or workflow. The recently proposed indirect transmission measurement (ITM) method42 needs at least the segmentation of one material class. When noise or artifacts are present in the reconstructed image, it causes incorrect material segmentation and yields an inferior estimate of the spectrum.
Dual-energy CT (DECT) scanners have been widely used in realistic applications. Although the x-ray spectrum is helpful for DECT material decomposition, especially for that in the projection domain, accurate estimation of the high- and low-energy x-ray spectra is not a trivial task. Compared with projection-domain material decomposition, image-domain material decomposition does not suffer from inconsistent rays issue and is more convenient in clinical applications as it is performed on CT images.43–45 In this case, the x-ray spectrum does not need to be involved in material decomposition. In addition, realistic projection-domain material decomposition used a phantom calibration fashion instead of a spectrum-involved method.46,47 With dual-energy material decomposition, this work aims to develop a segmentation-free, ITM-type energy spectrum estimation method using model spectra and a material images-based polychromatic forward projection.48
The paper is organized as follows: in Sec. 2, we describe our method for spectrum estimation and four major components of the method. In Sec. 3, we describe evaluation studies, which include numerical simulations, experimental phantom, and realistic images. Section 4 presents the results, and we conclude with a discussion and summary in Sec. 5.
2. Methods
To avoid determining each energy bin of the x-ray spectrum, we use model spectra to express the spectrum that is to be estimated. The model spectra expression can significantly reduce the degrees of freedom (DOFs) of the spectrum estimation problem. In this case, the unknown spectrum is the weighted summation of a set of model spectra , i.e.,
| (1) |
where is the number of the model spectra and is the weight on the respective model spectrum. The model spectra can be predetermined using spectrum generators (such as Spektr49 and SpekCalc50) or MC simulation toolkits based on Geant4.
The flowchart of the proposed algorithm is presented in Fig. 1. The method starts from raw projection data. Material-specific images are then calculated using dual-energy material decomposition algorithms. From the material images, along with the model spectra expression, a set of estimated projection is calculated. By iteratively updating the unknown weights , we can converge to a set of optimal to minimize the quadratic error between the measured raw projection and the estimated projection . The unknown spectrum is finally obtained using Eq. (1). The four major components of the approach will be detailed in the following subsections: dual-energy material decomposition, polychromatic projection on decomposed material images, weights estimation, and model spectra generation.
Fig. 1.
Flowchart of the proposed dual-energy material decomposition-based spectrum estimation method.
2.1. Dual-Energy Material Decomposition
To obtain quantitative material-specific basis images, we use a nonlinear empirical dual-energy calibration (EDEC) algorithm to perform material decomposition.46 For the EDEC technique, a two-cylinder calibration phantom with the same materials as the subsequent CT scan is used. The imaging protocol used in the calibration is the same as that used in the phantom studies. By minimizing the least-square deviation between a set of basis images and a corresponding template, one can calibrate the decomposition coefficients for each basis material. As magnified noise is a general concern for both projection-domain and image-domain dual-energy material decomposition and to keep the accuracy of the estimated projection , in this study, we also used an iterative image-domain method to obtain the significantly noise-reduced material-specific images.44 The method optimizes an objective function that consists of a data fidelity term and a quadratic penalty term using the nonlinear conjugate gradient algorithm. Using the regularization framework, the iterative image-domain material decomposition method provides material-specific images with noise that is well reduced and accuracy that is well preserved.
2.2. Polychromatic Projection on Decomposed Material Images
In dual-energy material decomposition, the linear attenuation coefficient is modeled with two basis materials via a weighted summation fashion as
| (2) |
Here, and are the known independent energy dependencies, which can be mass attenuation coefficients of basis materials, and and are the material-selective images. Based on the above formulation, polychromatic projection of an object is represented as
| (3) |
where and are the line integrals of the material-selective images. Here, , , and are the propagation path length of each ray, the corresponding polychromatic x-ray spectrum of the ray, and the maximum photon energy of the spectrum, respectively. is the energy-dependent response of the detector. Note that is the detector pixel dependent and the detector channel index is omitted for convenience. After applying the logarithmic operation, the estimated projection data can be expressed as
| (4) |
| (5) |
| (6) |
where
| (7) |
Note that the air scan data were used in Eq. (4) and is a function of unknown weights .
2.3. Weights Estimation
To estimate the unknown weights for each model spectrum, we minimize the quadratic error between the detector measurement and the corresponding estimated projection by iteratively updating the weights. This procedure is formulated as the following optimization problem:
| (8) |
Here, the normalization constraint and the non-negative constraint, which keeps the solution of the problem physically meaningful, are introduced. The objective function is a minimum when the spectrum expressed using the model spectra matches the unknown raw spectrum. To solve Eq. (8), we use a sequential optimization approach, i.e., minimizing the objective function, followed by normalizing the solution and enforcing a non-negative constraint sequentially. To minimize the objective function, we used a simple multivariable downhill simplex method. The calibration procedure can be summarized in Algorithm 1.
Algorithm 1.
Sequential optimization.
| 1. Set , choose . |
| 2. Repeat |
| 3. |
| 4. |
| 5. |
| 6. |
| 7. Until stopping criterion is satisfied. |
2.4. Model Spectra Generation
There are several different ways to obtain the model spectra, and they would affect the final results during the calibration procedure; thus, well-validated spectrum generators, which generate spectra with accurate physical properties (such as characteristic peak),22,49–52 need to be employed to calibrate the real spectrum. In this study, we used MC simulation toolkit Geant433 and the widely used software SpekCalc50 to produce the model spectra. For both methods, different thicknesses of filters are added to yield model spectra with different half-value layers. For the Geant4 model spectra simulation, we used monoenergetic electrons (pencil beam) to hit the tungsten target. The thickness of the target is 0.25 cm, and the target angle is 30 deg. For the SpekCalc model spectra, we set the target angle to 30 deg and added a 0.8-mm beryllium window. The energy bin width is 1 keV, and air thickness is 1000 mm.
3. Evaluations
3.1. Numerical Study
We first use numerical simulation to evaluate the proposed spectrum estimation method. A water cylinder with six iodine concentrate inserts (ranging 0 to with interval) was simulated in a 2-D fan-beam CT geometry. The diameter of the water cylinder is 198 mm, and the diameter of the six inserts is 22.5 mm. The low- and high-energy spectra are 100 and 140 kVp, respectively, and they were generated using the SpekCalc software50 with 12-mm Al and 0.4-mm Al filtration, respectively. For the x-ray detection, an energy-integrating detector was simulated with 0.388-mm pixel size and 1024 pixels. The x-ray source to isocenter distance (SOD) and source to detector distance (SDD) are 785 and 1200 mm, respectively. A set of 720 view angles was scanned in an angular range of 360 deg. As one difficulty of DECT decomposition is the ill conditioning, Poisson noise was introduced to the raw projection to show the robustness of the algorithm. In addition, first-order beam hardening correction was performed to improve the accuracy of the material-specific images. During dual-energy material decomposition, regions of interest (ROIs) in the central water cylinder and in the iodine concentrate insert are used to calculate the decomposition matrix.
To quantify the accuracy of the estimated spectrum, we calculate the normalized root mean square error (NRMSE) and the mean energy difference between the raw spectrum (ground truth) and the estimated spectrum, i.e.,
| (9) |
| (10) |
where is the ’th energy bin of the normalized estimated spectrum and is the ’th energy bin of the normalized true spectrum. and are the number of the energy bins and the energy of the ’th energy bin of the spectrum, respectively.
For the numerical simulation study, the raw spectrum used to generate the projection data and the model spectra used to calibrate the raw spectra are both obtained from SpekCalc software. To further cross check the robustness of the proposed method with respect to the model spectra, MC simulation toolkit Geant4 is also employed to generate the model spectra. Geant4 provides comprehensive physics process modeling that embedded in a flexible structure, and it offers a full list of electron interaction modeling, which makes an important role in x-ray generation, including the bremsstrahlung effect and characteristic radiation. In addition, Geant4 collaboration has consistently released the G4EMLOW low-energy package that enables access to precise cross sections for x-ray photons production at a very low-energy scale.
In this study, eight model spectra are generated with different thicknesses of aluminum filtration with SpekCalc and Geant4. For the SpekCalc model spectra, the filtration is from 2 to 30 mm in steps of 4 mm, whereas for the Geant4 model spectra, the filtration is from 8 to 22 mm in steps of 2 mm. During each MC simulation, a total number of electrons are emitted to hit the target.
3.2. Comparison Study
To further evaluate the performance of the proposed method, the method is compared with the previous segmentation-based ITM spectrum estimation method.42 Different from the ITM method, the proposed DECT-based method does not require a dedicated phantom calibration and image segmentation. To demonstrate this feature, we performed spectrum estimation using a numerical anthropomorphic thorax phantom. In this study, to show the advantage of the DECT-based method, we estimated the spectrum with both standard attenuation coefficients and intended mismatched attenuation coefficients. That is, raw projection data are first generated using standard National Institute of Standards and Technology (NIST) attenuation coefficients and then reconstructed to obtain CT images. For the segmentation-based method, the spectrum is estimated based on the segmented CT image, which is assigned to standard coefficients. For the DECT-based method, the EDEC algorithm46 is employed to generate material images.
As the attenuation coefficients of a realistic patient or object may deviate from the standard value, for example, a fatty body may have lower attenuation coefficient than the standard value, we then further estimate the spectrum using intended mismatched attenuation coefficients. In this case, raw projection data were generated using 98% standard attenuation coefficients for both bone and tissue. Then both methods were employed to estimate the spectrum based on the raw projection data.
3.3. Experimental Phantom Study
The algorithm was also evaluated using experimental phantom data acquired with a cone-beam CT (CBCT) benchtop system and an in-house rotating gantry small animal micro-CT scanner, which was developed by the authors.
3.3.1. Benchtop cone-beam computed tomography
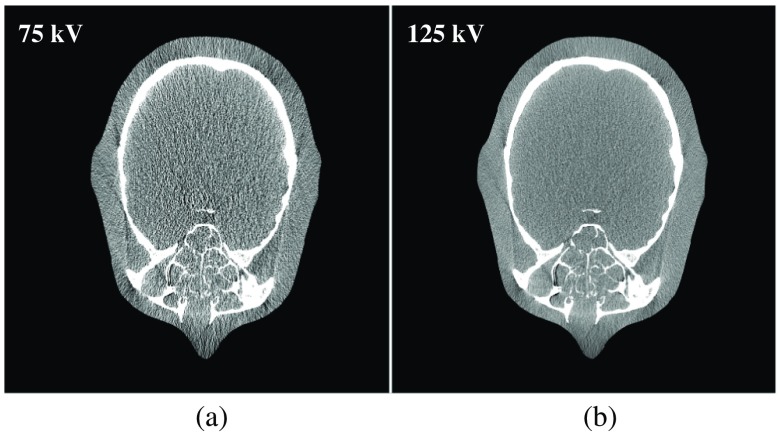
An anthrophomorphic head phantom was scanned using the CBCT benchtop system. The SOD and SDD were 1000 and 1500 mm, respectively. A total of 655 projections were evenly acquired in 360 deg rotation with rebinning mode and narrow collimation to avoid scatter radiation. Tube potentials of high- and low-energy spectra were 125 and 75 kVp, respectively. During CT data acquistion, the x-ray source (Rad 94, Varian, Palo Alto, California) and the flat detector (PaxScan 4030D, Varian, Palo Alto, California) were stationary, and the phantom was rotated to acquire projection from different view angles. The pixel matrix and size of the detector are and , respectively. A prefiltering of 6.0-mm aluminum was always applied, and the reference spectrum was simulated using SpekCalc with the filtration matched with the prefilter. Because of the large phantom size, scatter radiation would play an important role in projection. To reduce the impact of scatter radiation on the accuracy of the estimated spectrum, we acquired the data using narrow collimation.
3.3.2. Small animal microcomputed tomography
A simplified mice phantom was scanned using a small animal micro-CT scanner, which was developed by the authors in a gantry rotating geometry, as shown in Fig. 2. The x-ray source (L9421-02, Hammamatsu Photonics, Hammamatsu City, Japan) and detector (Dexela 1207, PerkinElmer, Waltham, Massachusetts) were assembled on the rotating gantry while the phantom was kept stationary during the CT scan. The pixel matrix and size of the detector are and , respectively. The SOD and SDD were 229 and 416 mm, respectively. A total of 450 projections were acquired for image reconstruction. To perform dual-energy CT imaging, the phantom was scanned with a low-energy spectrum (40 kV with 2-mm aluminum filtration) and a high-energy spectrum (90 kV with 0.3-mm copper filtration) in a sequential mode. For both phantom studies, low- and high-energy CT images were reconstructed using a filtered backprojection algorithm. Low-energy data sets were used to estimate low-energy spectra, and high-energy spectra estimation followed the same procedure.
Fig. 2.
Experimental phantom study using the small animal CT scanner. (a) The system geometry for the CT scanner is rotating gantry, and the x-ray tube and detector are assembled on the gantry while the specimen lies stationary on the table between the x-ray source and the detector. (b) Phantom scanned using the micro-CT scanner.
3.4. Realistic Images Evaluation
To further evaluate the proposed method, we generated high- and low-energy projection data by forward projecting two sets of abdomen images, which were acquired from a dual-source dual-energy CT scanner (Siemens SOMATOM Definition Flash, Siemens AG, Forchheim, Germany). The system enables high- and low-energy CT scans with two x-ray tubes and corresponding detectors mounted onto a single rotating gantry with a 90 deg angular offset. The x-ray tubes can operated independently with regard to tube filtration, tube voltage, and tube current. Low- and high-energy projection data were obtained with 100 and 140 kVp spectra, respectively. Images were reconstructed using the built-in commercial software.
Based on these CT images, a graphics processing unit-based forward-projecting program was used to generate the high- and low-energy “realistic” abdomen projection images, and these projection data sets were applied to spectra estimation. An iterative image-domain material decomposition method was used to yield noise-reduced material-selective images. The iteration number was set to 200, and the control parameter , which balances the data fidelity term and the regularization term, was set to 0.015. During the calibration procedure, eight model spectra were used. These spectra were generated using SpekCalc with an aluminum filter ranging from 6 to 20 mm with 2-mm interval. Note that, in this evaluation, we did not have true spectrum, i.e., there was no ground truth for comparison. Thus, we compared the forward projection data with the estimated projection when the optimization problem was converged.
4. Results
4.1. Numerical Simulation
Figure 3 shows the results of low- and high-energy CT images of the numerical iodine concentrate phantom. As can be seen, 100-kV image shows much higher contrast level for the iodine inserts, as expected. During material decomposition, ROIs in the central area of the numerical phantom and in the are used to calculate the decomposition matrix.
Fig. 3.
(a) Low- and (b) high-energy CT images () of the numerical water phantom containing inserts with different iodine concentrates.
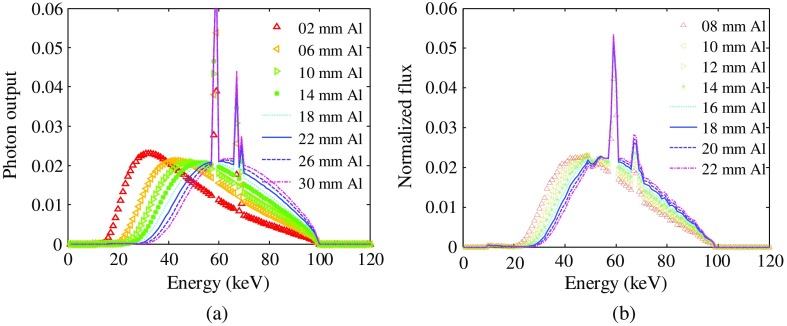
Model spectra used in the spectrum calibration procedure are shown in Fig. 4. To evaluate the robustness of the proposed spectrum estimation method with respect to the model spectra generator, different methods are employed to obtain the model spectra. Figure 4(a) shows the 100-kV model spectra generated using SpekCalc software with fixed kVp setting and different thicknesses of filtration ranging from 2 to 30 mm in steps of 4 mm. Figure 4(b) shows model spectra simulated using MC toolkit Geant4 with filtration ranging from 8 to 22 mm in steps of 2 mm. Because of the limited electron events emitted in the MC simulation, the Geant4 model spectra contain some noise, which may impact the final result. For both model spectra, the spectrum becomes harder and narrower as the thickness of the filtration increases.
Fig. 4.
100 kVp model spectra generated using SpekCalc (a) and MC toolkit Geant4 (b) with different thicknesses of aluminum filtration. Note that the noise level of the Geant4 model spectra is relatively high due to the limited 100-keV electron events.
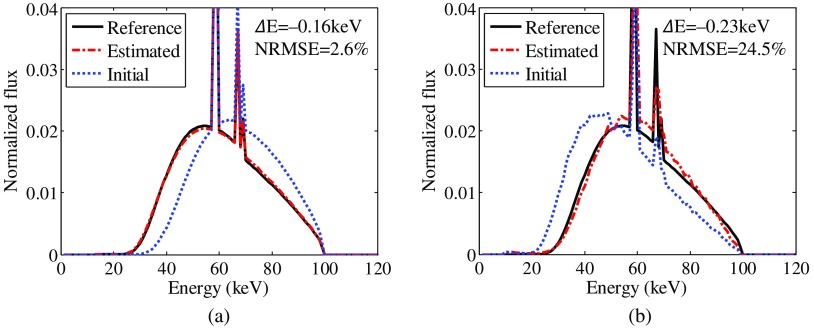
Figure 5 shows the results of the 100-kV spectrum estimation for the numerical phantom data using both SpekCalc and Geant4 model spectra. The initial spectrum to calibrate the unknown weights is the hardest and softest model spectra for the SpekCalc and Geant4 model spectra estimation, respectively. The reference spectrum is the spectrum that was used to generate the 100-kV projection data, and it can be regarded as the ground truth. The estimated spectrum matches the reference spectrum quite well when SpekCalc model spectra are used [as shown in Fig. 5(a)], and and NRMSE are and 2.6%, respectively, suggesting the dual-energy material decomposition-based method provides an accurate spectrum estimate.
Fig. 5.
X-ray spectra estimated for the numerical iodine concentrate phantom data. Model spectra generated using both (a) SpekCalc and (b) Geant4 were employed in the estimation procedure. The initial guesses for the sequential optimization problem correspond to the hardest and softest model spectra for the SpekCalc and Geant4 model spectra estimation, respectively. As the Geant4 model spectra are relatively noisy, spectrum estimated using these spectra is also noisy.
For the numerical simulation studies, as the raw projection is produced by the polychromatic forward projection using the SpekCalc spectrum, spectrum estimation using different model spectra is also conducted, which could be a cross check for the proposed method. Figure 5(b) shows the spectrum estimated using Geant4 model spectra, and there is some noise in the estimated spectrum. This noise comes from the Geant4 model spectra as shown in Fig. 4(b). Although the presence of noise causes a significantly increased NRMSE between the estimated spectrum and the true spectrum, their mean energy difference is , which is still comparable with that of spectrum estimation using SpekCalc model spectra.
Although the model spectra affect the final result, the proposed method tends to yield an optimal spectrum that minimizes the quadratic error of the raw projection data and the estimated reprojection data using the different model spectra. Figure 6 shows the residual between the raw projection data and the estimated projection data as the iteration number of the optimization problem increases for the numerical simulation. For both model spectra, the objective function [Eq. (8)] converges to the same level, indicating that the optimization procedure is robust against the model spectra. This is why the mean energy difference can remain at the same level for different model spectra.
Fig. 6.
Residual between the raw projection and the estimated projection as the iteration number increases for the numerical iodine concentrate phantom data.
As dual-energy material decomposition would amplify the image noise, which may affect the final result, spectrum estimation using different numbers of primary photon events (i.e., dose levels) is performed to demonstrate the robustness of the proposed method. The first, second, and third rows of Fig. 7 show x-ray spectra estimated from the numerical phantom data using , , and photon histories, respectively. The first column of Fig. 7 shows the spectrum estimated using material-specific images obtained from direct matrix inversion (i.e., without noise reduction), whereas the second column of Fig. 7 shows the spectrum estimated using material-specific images obtained from the iterative image-domain material decomposition method (i.e., with noise reduction). As can be seen, for different noise levels, the proposed method can accurately recover the true spectrum. For different dose levels, the maximum is 0.56 keV, and the maximum NRMSE is 3.8%.
Fig. 7.
X-ray spectra estimated from the numerical phantom at different numbers of primary photon events. (a, c, e) use direct matrix inversion to obtain the material images for the spectrum estimation, whereas (b, d, f) use a noise-reduced dual-energy material decomposition method (i.e., iterative image-domain method) for the spectrum estimation. The numbers of the primary photon events used in the numerical simulations of the low-energy CT scans for (a, b), (c, d), and (e, f) are , , and , respectively. For each of the dual-energy CT scans, the numbers of the photon events of the high-energy CT scans are half of the respective low-energy CT scans.
4.2. Comparison Studies
Figure 8 shows the results of spectra estimation using the anthropomorphic thorax phantom. Figures 8(a) and 8(b) are the polychromatic 100 and 140-kV CT images, respectively. Compared with the 140-kV image, there are more beam hardening artifacts in the 100-kV image. Figures 8(c) and 8(d) show the segmentation-based and the proposed DECT-based spectra estimations using raw projection data obtained with standard attenuation coefficients. As can be seen, both methods can accurately estimate the spectrum. The NRMSE between the estimated spectra and their reference for the segmentation-based method and the DECT-based method are 4.4% and 4.5%, respectively. Figures 8(e) and 8(f) show the segmentation-based and the DECT-based spectra estimations using the raw projection data obtained with 98% standard attenuation coefficients. As can be seen, for the nonstandard material, the NRMSE of the estimated spectrum using the segmentation-based method is increased from 4.4% to 8.2%. However, for the DECT-based method, the accuracy of the estimated spectrum is well preserved.
Fig. 8.
Results of energy spectrum estimation using the anthropomorphic thorax phantom. (a) and (b) are the 100 and 140-kV CT images, respectively. Display window for the images: ( and 150 HU). (c) and (d) are the segmentation-based and the proposed DECT-based spectra estimations using the raw projection data acquired with standard attenuation coefficients, respectively. (e) and (f) are the segmentation-based and the DECT-based spectra estimations, respectively, using the raw projection data acquired with 98% attenuation coefficients.
4.3. Experimental Phantom Studies
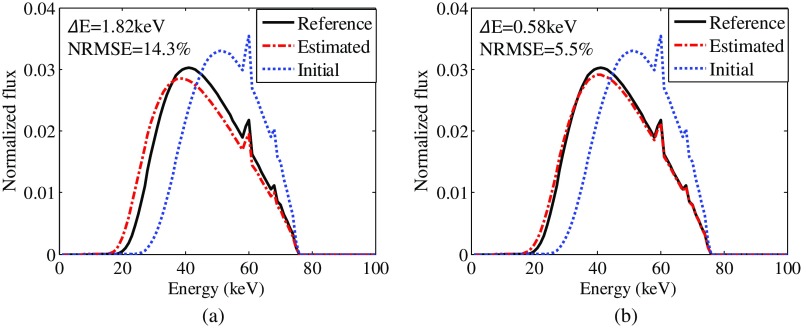
Figure 9 shows low- and high-energy CT images of the experimental head phantom. Figure 10 shows the spectrum estimated with the anthrophomorphic head phantom with and without detector efficiency incorporation. For this experimental evaluation, the benchtop CBCT system used a flat detector with 0.6-mm thickness of CsI. To better estimate the spectrum, energy-dependent efficiency should be taken into account. is reduced from 1.82 to 0.58 keV after detector efficiency incorporation, whereas NRMSE is reduced from 14.3% to 5.5% after detector efficiency incorporation. For both cases, the initial spectra for the constrained optimization problem are the hardest model spectra. The reference true spectrum is generated using SpekCalc with filtration that matches the filtration used in the experimental data acquisition.
Fig. 9.
(a) Low- and (b) high-energy CT images of the experimental head phantom. Display window: ( and 300 HU).
Fig. 10.
Spectra estimated using the physical head phantom (b) with and (a) without detector efficiency incorporation.
Figure 11 shows low- and high-energy CT images of the mice phantom scanned using the in-house micro-CT scanner. Figure 12 shows the estimated low-energy spectrum. The initial spectrum for the constrained optimization problem is the hardest model spectra. The reference true spectrum is generated using SpekCalc with filtration that matches the filtration used in the experimental data acquisition.
Fig. 11.
(a) Low- and (b) high-energy CT images of the mice phantom scanned using the micro-CT scanner. Display window: ( and 600 HU).
Fig. 12.
Spectra estimated using the mice phantom. The initial spectrum for the optimization problem is the hardest model spectra.
4.4. Realistic Images Evaluations
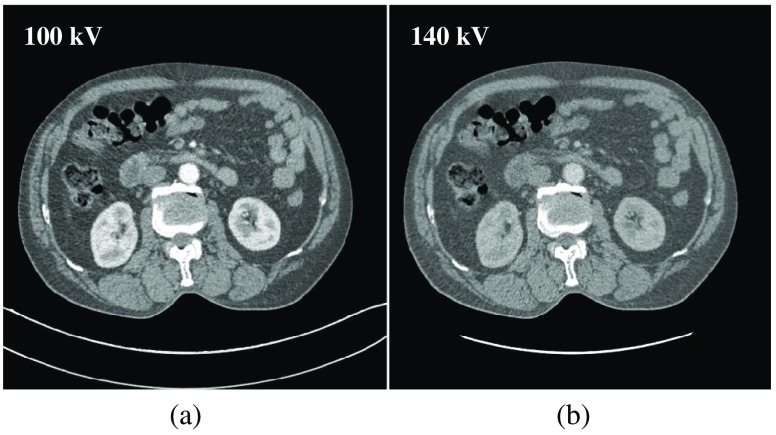
To confirm the results of the numerical and experimental phantom studies, we used realistic patient data obtained by forward projecting two abdomen CT images. These two CT images (as shown in Fig. 13) were acquired and reconstructed with a Siemens SOMATOM Definiton Flash scanner under 100 and 140 kV. The forward projection data sets are used to mimic dual-energy low- and high-energy raw projection data.
Fig. 13.
Axial contrast-enhanced, dual-energy abdominal CT scan using Siemens SOMATOM definition flash CT scanner. (a) and (b) show low- and high-energy CT images, respectively. Display window: ( and 300 HU).
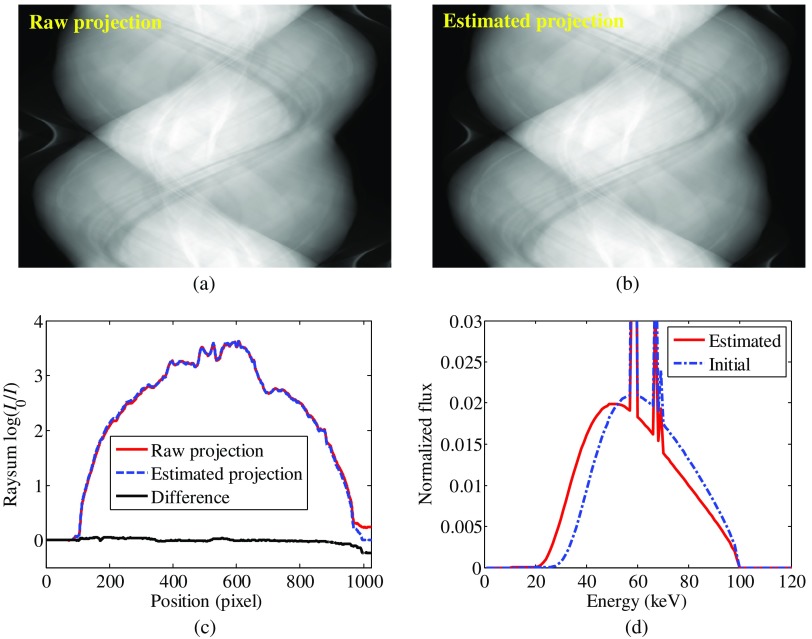
During dual-energy material decomposition, adipose and iodine are chosen as the basis materials. For this evaluation, the true spectrum, which is employed in the raw projection data acquisition, is not available; therefore, we compare the raw projection data with the estimated projection, which is calculated using the estimated spectrum when the objective function is converged. Figure 14 shows raw projection, estimated projection, their line profiles, and the estimated spectrum. The final estimated projection matches the raw projection quite well, indicating that the proposed method can be applied to realistic cases.
Fig. 14.
Results for realistic abdomen images evaluation. (a) Raw projection obtained by forward projecting the 100-kV CT image. (b) Estimated projection obtained using the estimated 100-kV spectrum. (c) Line profiles comparison of the raw projection and the estimated projection. (d) The estimated spectrum and the initial spectrum used in the optimization problem. Note that true spectrum is not available in this case and the estimated spectrum should be an effective spectrum, which takes the system configuration and postprocessing algorithms into account.
5. Discussion
In this study, we present a polychromatic x-ray spectrum estimation method based on dual-energy material decomposition. Different from the method proposed in Ref. 42, where a segmentation procedure is needed for polychromatic reprojection, here, polychromatic reprojection is performed on material-specific images that were obtained by dual-energy material decomposition. This enables the proposed method to be segmentation-free. More importantly, based on the DECT material decomposition, the proposed method can be further applied to phantom or patient data whose attenuation coefficients are unknown. This enables the proposed DECT-based technique to be applied to more realistic and general applications. Namely, the proposed method does not require a dedicated phantom calibration. Hence, the method can be regarded as a major step toward spectrum estimation of realistic applications without breaking the current workflow.
In realistic applications, the x-ray spectrum is affected by many parameters, such as focal spot size and thickness of the target. In addition, the incident electrons used for hitting the target are also polychromatic. Thus, it is almost impossible to model all of the parameters and physical effects to obtain the true spectrum. Instead, the proposed method uses model spectra to span a space, and the spectrum calibration procedure is used to find an optimal spectrum in the space to generate a reprojection data set whose difference is as small as possible from the raw projection data, i.e., the optimal spectrum has the most similar attenuation property as the true spectrum. Model spectra should affect the final results as indicated in Fig. 5. However, no matter what model spectra are used, the proposed method tends to yield a spectrum that minimizes the quadratic error between the raw projection and estimated projection as characterized by the objective function of Eq. (8). To our belief, the NRMSE could be significantly reduced if the Geant4 model spectra contain less noise in the numerical simulation study. Nevertheless, some widely used and well-validated spectrum generators, including SpekCalc and Spektr, are suggested to generate model spectra for this method. For the weights calibration, as no automatic exposure control is used in the numerical studies or the experimental phantom study, we only use projection in one view angle to estimate the spectrum, and the calibration time is on a personal PC (Intel Core i7-6700K CPU).
To reduce the DOFs of the spectrum estimation problem, we employed a linear model (i.e., the unknown spectrum is expressed as a linear combination of a set of model spectra). However, using the linear model is unnecessary, and other models, such as a nonlinear model, can be used to express the unknown spectrum. In this case, a simple curve and its widening or deforming versions can be used as model spectra. To better recover the unknown, we should also take advantage of the prior knowledge of an x-ray spectrum, namely an x-ray spectrum contains characteristic x-rays and bremsstrahlung. Hence, some constraints should be added to the simple curve and its transformations. This is why we used filtered model spectra to fit the true spectrum in this study, and these spectra can also be regarded as transformations (deformed by a polychromatic Beer’s law) of a simple polychromatic x-ray spectrum. In future study, we would like to estimate the unknown spectrum using model spectra derived from a simple spectrum with the same kVp as the unknown spectrum and its high-order transformations (such as filtered using different materials).
For the experimental phantom study, the discrepancy between the estimated spectrum and the raw spectrum is much larger than that in the simulation study. The discrepancy can be attributed to the following three aspects. First, scatter is not considered in the reprojection procedure; thus, the inevitable concomitant scatter radiation in the raw projection data would affect the accuracy of the spectrum result. To further refine the result, one may want to perform scatter correction53 before spectrum estimation. Second, for the material images-based polychromatic forward projection, the attenuation coefficients of the materials (bone and tissue) were obtained from the NIST database. These values may deviate from the real values of the head phantom. Third, the detector housing and sensor protection material would also affect the accuracy of the estimated spectrum.
For the realistic patient study, we do not have access to the raw projection data on real scanners. In this case, we only have CT images, and the images usually have performed water correction. If one simply forward projects the corrected CT images and then uses the projection to estimate the spectrum, the resulting spectrum should be an effective spectrum, which takes the contribution of the beam hardening procedure into account.
6. Conclusions
This work presents an x-ray energy spectrum calibration method for CT scanners using dual-energy material decomposition and the ITM framework. The method performs polychromatic reprojection using material-specific images instead of segmented CT images, with which the segmentation procedure is avoided. The reprojection data are then compared with the raw projection data, and their difference is minimized by iteratively updating a set of weights, which are used to express the unknown spectrum together with a set of model spectra. The method was evaluated using numerical simulation data, experimental phantom data, and realistic patient data. The results demonstrate that raw spectra can be accurately recovered by incorporating the energy-dependent detector absorption efficiency. The method does not require dedicated phantom calibration or knowledge of the material attenuation coefficient. It is promising for spectrum estimation of realistic applications.
Acknowledgments
This work was supported by the Zhejiang Provincial Natural Science Foundation of China (Grant No. LR16F010001), National High-Tech R&D Program for Young Scientists by the Ministry of Science and Technology of China (Grant No. 2015AA020917), National Key Research Plan by the Ministry of Science and Technology of China (Grant No. 2016YFC0104507), Natural Science Foundation of China (NSFC Grant Nos. 81201091, 61601190, and 51305257), and National Institutes of Health (NIH 1R01 EB016777).
Biographies
Wei Zhao received his PhD in particle physics and nuclear physics from the Institute of High Energy Physics, Chinese Academy of Sciences, in 2012. He is currently a research scientist in the Department of Radiation Oncology at Stanford University. His research interests are CT system development and x-ray imaging methods and devices. He is an NSFC-funded investigator.
Lei Xing received his PhD from Johns Hopkins University in 1992. He is currently the Jacob Haimson professor of medical physics and the director of the medical physics division of the Radiation Oncology Department at Stanford University. His research focuses on inverse treatment planning, tomographic image reconstruction, CT, optical and positron emission tomography (PET) imaging instrumentations, image guided interventions, nanomedicine, and applications of molecular imaging in radiation oncology. He is an NIH, DOD, NSF, ACS-funded investigator and is active in numerous professional organizations. He is a fellow of the AAPM and AIMBE.
Qiude Zhang received his BS and MS degrees in biomedical engineering from Huazhong University of Science and Technology in 2013 and 2016, respectively. His research interest is CT system and x-ray detector development.
Qingguo Xie received his PhD in control theory and control engineering from Huazhong University of Science and Technology (HUST) in 2001. He is currently a professor of biomedical engineering at HUST, where he directs the digital PET Lab. His research interests include system development and clinical application of PET. He is an NSFC-funded investigator.
Tianye Niu received his BS degree in modern physics and his PhD in physical electronics from the University of Science and Technology of China in 2008. He is currently a professor of biomedical engineering in the School of Medicine at Zhejiang University. His research interests include system development and clinical application of CT. He is an NSFC-funded investigator.
Disclosures
The authors have no conflicts of interest to declare.
References
- 1.DeMarco J., et al. , “A Monte Carlo based method to estimate radiation dose from multidetector CT (MDCT): cylindrical and anthropomorphic phantoms,” Phys. Med. Biol. 50(17), 3989–4004 (2005). 10.1088/0031-9155/50/17/005 [DOI] [PubMed] [Google Scholar]
- 2.Elbakri I. A., Fessler J. A., “Statistical image reconstruction for polyenergetic x-ray computed tomography,” IEEE Trans. Med. Imaging 21(2), 89–99 (2002). 10.1109/42.993128 [DOI] [PubMed] [Google Scholar]
- 3.Nuyts J., et al. , “Modelling the physics in the iterative reconstruction for transmission computed tomography,” Phys. Med. Biol. 58(12), R63 (2013). 10.1088/0031-9155/58/12/R63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhao W., et al. , “Using edge-preserving algorithm with non-local mean for significantly improved image-domain material decomposition in dual-energy CT,” Phys. Med. Biol. 61(3), 1332–1351 (2016). 10.1088/0031-9155/61/3/1332 [DOI] [PubMed] [Google Scholar]
- 5.Long Y., Fessler J. A., “Multi-material decomposition using statistical image reconstruction for spectral CT,” IEEE Trans. Med. Imaging 33(8), 1614–1626 (2014). 10.1109/TMI.2014.2320284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xi Y., et al. , “United iterative reconstruction for spectral computed tomography,” IEEE Trans. Med. Imaging 34(3), 769–778 (2015). 10.1109/TMI.2014.2339497 [DOI] [PubMed] [Google Scholar]
- 7.Zhao Y., Zhao X., Zhang P., “An extended algebraic reconstruction technique (E-ART) for dual spectral CT,” IEEE Trans. Med. Imaging 34(3), 761–768 (2015). 10.1109/TMI.2014.2373396 [DOI] [PubMed] [Google Scholar]
- 8.Zhao W., et al. , “Energy spectrum extraction and optimal imaging via dual-energy material decomposition,” in IEEE Nuclear Science Symp. and Medical Imaging Conf. (NSS/MIC 2015), pp. 1–4, IEEE; (2015). 10.1109/NSSMIC.2015.7582159 [DOI] [Google Scholar]
- 9.Taguchi K., et al. , “Enabling photon counting clinical x-ray CT,” in IEEE Nuclear Science Symp. Conf. Record (NSS/MIC 2009), pp. 3581–3585, IEEE; (2009). 10.1109/NSSMIC.2009.5401823 [DOI] [Google Scholar]
- 10.Taguchi K., Iwanczyk J. S., “Vision 20/20: single photon counting x-ray detectors in medical imaging,” Med. Phys. 40(10), 100901 (2013). 10.1118/1.4820371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yaffe M., Taylor K., Johns H., “Spectroscopy of diagnostic x-rays by a Compton-scatter method,” Med. Phys. 3(5), 328–334 (1976). 10.1118/1.594263 [DOI] [PubMed] [Google Scholar]
- 12.Matscheko G., Ribberfors R., “A compton scattering spectrometer for determining x-ray photon energy spectra,” Phys. Med. Biol. 32(5), 577–594 (1987). 10.1088/0031-9155/32/5/004 [DOI] [PubMed] [Google Scholar]
- 13.Gallardo S., Ródenas J., Verdú G., “Monte Carlo simulation of the compton scattering technique applied to characterize diagnostic x-ray spectra,” Med. Phys. 31(7), 2082–2090 (2004). 10.1118/1.1759827 [DOI] [PubMed] [Google Scholar]
- 14.Llovet X., et al. , “Monte Carlo simulation of x-ray spectra generated by kilo-electron-volt electrons,” J. Appl. Phys. 93(7), 3844–3851 (2003). 10.1063/1.1545154 [DOI] [Google Scholar]
- 15.Ay M., et al. , “Monte Carlo simulation of x-ray spectra in diagnostic radiology and mammography using MCNP4C,” Phys. Med. Biol. 49(21), 4897–4917 (2004). 10.1088/0031-9155/49/21/004 [DOI] [PubMed] [Google Scholar]
- 16.Mainegra-Hing E., Kawrakow I., “Efficient x-ray tube simulations,” Med. Phys. 33(8), 2683–2690 (2006). 10.1118/1.2219331 [DOI] [PubMed] [Google Scholar]
- 17.Bazalova M., Verhaegen F., “Monte Carlo simulation of a computed tomography x-ray tube,” Phys. Med. Biol. 52(19), 5945–5955 (2007). 10.1088/0031-9155/52/19/015 [DOI] [PubMed] [Google Scholar]
- 18.Miceli A., et al. , “Comparison of simulated and measured spectra of an industrial 450kv x-ray tube,” Nucl. Instrum. Methods Phys. Res., Sect. A 580(1), 123–126 (2007). 10.1016/j.nima.2007.05.025 [DOI] [Google Scholar]
- 19.Birch R., Marshall M., “Computation of bremsstrahlung x-ray spectra and comparison with spectra measured with a Ge (Li) detector,” Phys. Med. Biol. 24(3), 505–517 (1979). 10.1088/0031-9155/24/3/002 [DOI] [PubMed] [Google Scholar]
- 20.Tucker D. M., Barnes G. T., Chakraborty D. P., “Semiempirical model for generating tungsten target x-ray spectra,” Med. Phys. 18(2), 211–218 (1991). 10.1118/1.596709 [DOI] [PubMed] [Google Scholar]
- 21.Boone J. M., Seibert J. A., “An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kv,” Med. Phys. 24(11), 1661–1670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]
- 22.Hernandez A., Boone J., “Tungsten anode spectral model using interpolating cubic splines: unfiltered x-ray spectra from 20 kv to 640 kv,” Med. Phys. 41(4), 042101 (2014). 10.1118/1.4866216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Archer B. R., Wagner L. K., “A Laplace transform pair model for spectral reconstruction,” Med. Phys. 9(6), 844–847 (1982). 10.1118/1.595193 [DOI] [PubMed] [Google Scholar]
- 24.Hassler U., Garnero L., Rizo P., “X-ray dual-energy calibration based on estimated spectral properties of the experimental system,” IEEE Trans. Nucl. Sci. 45(3), 1699–1712 (1998). 10.1109/23.685292 [DOI] [Google Scholar]
- 25.Waggener R. G., et al. , “X-ray spectra estimation using attenuation measurements from 25 kVp to 18 MV,” Med. Phys. 26(7), 1269–1278 (1999). 10.1118/1.598622 [DOI] [PubMed] [Google Scholar]
- 26.Lin Y., et al. , “An angle-dependent estimation of CT x-ray spectrum from rotational transmission measurements,” Med. Phys. 41(6), 062104 (2014). 10.1118/1.4876380 [DOI] [PubMed] [Google Scholar]
- 27.Chang S., Mou X., “A statistical iterative reconstruction framework for dual energy computed tomography without knowing tube spectrum,” Proc. SPIE 9967, 99671L (2016). 10.1117/12.2236588 [DOI] [Google Scholar]
- 28.Perkhounkov B., et al. , “X-ray spectrum estimation from transmission measurements by an exponential of a polynomial model,” Proc. SPIE 9783, 97834W (2016). 10.1117/12.2217100 [DOI] [Google Scholar]
- 29.Hammersberg P., et al. , “Measurements of absolute energy spectra for an industrial micro focal x-ray source under working conditions using a compton scattering spectrometer,” J. X-Ray Sci. Technol. 8(1), 5–18 (1998). [PubMed] [Google Scholar]
- 30.Wilkinson L., Johnston P., Heggie J., “A comparison of mammography spectral measurements with spectra produced using several different mathematical models,” Phys. Med. Biol. 46(5), 1575–1589 (2001). 10.1088/0031-9155/46/5/316 [DOI] [PubMed] [Google Scholar]
- 31.Maeda K., Matsumoto M., Taniguchi A., “Compton-scattering measurement of diagnostic x-ray spectrum using high-resolution Schottky CdTe detector,” Med. Phys. 32(6), 1542–1547 (2005). 10.1118/1.1921647 [DOI] [PubMed] [Google Scholar]
- 32.Duisterwinkel H., et al. , “Spectra of clinical ct scanners using a portable compton spectrometer,” Med. Phys. 42(4), 1884–1894 (2015). 10.1118/1.4915497 [DOI] [PubMed] [Google Scholar]
- 33.Allison J., et al. , “Geant4 developments and applications,” IEEE Trans. Nucl. Sci. 53(1), 270–278 (2006). 10.1109/TNS.2006.869826 [DOI] [Google Scholar]
- 34.Taschereau R., et al. , “A microCT x-ray head model for spectra generation with Monte Carlo simulations,” Nucl. Instrum. Methods Phys. Res., Sect. A 569(2), 373–377 (2006). 10.1016/j.nima.2006.08.038 [DOI] [Google Scholar]
- 35.Miceli A., et al. , “Monte Carlo simulations of a high-resolution x-ray CT system for industrial applications,” Nucl. Instrum. Methods Phys. Res., Sect. A 583(2), 313–323 (2007). 10.1016/j.nima.2007.09.012 [DOI] [Google Scholar]
- 36.Guthoff M., et al. , “Geant4 simulation of a filtered x-ray source for radiation damage studies,” Nucl. Instrum. Methods Phys. Res., Sect. A 675, 118–122 (2012). 10.1016/j.nima.2012.01.029 [DOI] [Google Scholar]
- 37.Zhang L., et al. , “X-ray spectrum estimation from transmission measurements using the expectation maximization method,” in IEEE Nuclear Science Symp. Conf. Record (NSS 2007), Vol. 4, pp. 3089–3093, IEEE; (2007). 10.1109/NSSMIC.2007.4436783 [DOI] [Google Scholar]
- 38.Duan X., et al. , “CT scanner x-ray spectrum estimation from transmission measurements,” Med. Phys. 38(2), 993–997 (2011). 10.1118/1.3547718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lee J.-S., Chen J.-C., “A single scatter model for x-ray CT energy spectrum estimation and polychromatic reconstruction,” IEEE Trans. Med. Imaging 34(6), 1403–1413 (2015). 10.1109/TMI.2015.2395438 [DOI] [PubMed] [Google Scholar]
- 40.Sidky E. Y., et al. , “A robust method of x-ray source spectrum estimation from transmission measurements: demonstrated on computer simulated, scatter-free transmission data,” J. Appl. Phys. 97(12), 124701 (2005). 10.1063/1.1928312 [DOI] [Google Scholar]
- 41.Koenig T., et al. , “Imaging properties of small-pixel spectroscopic x-ray detectors based on cadmium telluride sensors,” Phys. Med. Biol. 57(21), 6743–6759 (2012). 10.1088/0031-9155/57/21/6743 [DOI] [PubMed] [Google Scholar]
- 42.Zhao W., et al. , “An indirect transmission measurement-based spectrum estimation method for computed tomography,” Phys. Med. Biol. 60(1), 339–357 (2015). 10.1088/0031-9155/60/1/339 [DOI] [PubMed] [Google Scholar]
- 43.Maass C., Baer M., Kachelriess M., “Image-based dual energy CT using optimized precorrection functions: a practical new approach of material decomposition in image domain,” Med. Phys. 36(8), 3818–3829 (2009). 10.1118/1.3157235 [DOI] [PubMed] [Google Scholar]
- 44.Niu T., et al. , “Iterative image-domain decomposition for dual-energy CT,” Med. Phys. 41(4), 041901 (2014). 10.1118/1.4866386 [DOI] [PubMed] [Google Scholar]
- 45.Mendonca P. R., Lamb P., Sahani D. V., “A flexible method for multi-material decomposition of dual-energy CT images,” IEEE Trans. Med. Imaging 33(1), 99–116 (2014). 10.1109/TMI.2013.2281719 [DOI] [PubMed] [Google Scholar]
- 46.Stenner P., Berkus T., Kachelriess M., “Empirical dual energy calibration (EDEC) for cone-beam computed tomography,” Med. Phys. 34(9), 3630–3641 (2007). 10.1118/1.2769104 [DOI] [PubMed] [Google Scholar]
- 47.Wu D., et al. , “A weighted polynomial based material decomposition method for spectral x-ray CT imaging,” Phys. Med. Biol. 61(10), 3749–3783 (2016). 10.1088/0031-9155/61/10/3749 [DOI] [PubMed] [Google Scholar]
- 48.Zhao W., Zhang Q., Niu T., “Segmentation-free x-ray energy spectrum estimation for computed tomography,” Proc. SPIE 9783, 978339 (2016). 10.1117/12.2216196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Siewerdsen J., et al. , “Spektr: a computational tool for x-ray spectral analysis and imaging system optimization,” Med. Phys. 31(11), 3057–3067 (2004). 10.1118/1.1758350 [DOI] [PubMed] [Google Scholar]
- 50.Poludniowski G., et al. , “Spekcalc: a program to calculate photon spectra from tungsten anode x-ray tubes,” Phys. Med. Biol. 54(19), N433 (2009). 10.1088/0031-9155/54/19/N01 [DOI] [PubMed] [Google Scholar]
- 51.Hernández G., Fernández F., “A model of tungsten anode x-ray spectra,” Med. Phys. 43(8), 4655–4664 (2016). 10.1118/1.4955120 [DOI] [PubMed] [Google Scholar]
- 52.Punnoose J., et al. , “Technical note: spektr 3.0—a computational tool for x-ray spectrum modeling and analysis,” Med. Phys. 43(8), 4711–4717 (2016). 10.1118/1.4955438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhu L., et al. , “Scatter correction for cone-beam CT in radiation therapy,” Med. Phys. 36(6), 2258–2268 (2009). 10.1118/1.3130047 [DOI] [PMC free article] [PubMed] [Google Scholar]