A new computational method for the detection of horizontal gene transfer events

Abstract

In recent years, the increase in the amounts of available genomic data has made it easier to appreciate the extent by which organisms increase their genetic diversity through horizontally transferred genetic material. Such transfers have the potential to give rise to extremely dynamic genomes where a significant proportion of their coding DNA has been contributed by external sources. Because of the impact of these horizontal transfers on the ecological and pathogenic character of the recipient organisms, methods are continuously sought that are able to computationally determine which of the genes of a given genome are products of transfer events. In this paper, we introduce and discuss a novel computational method for identifying horizontal transfers that relies on a gene's nucleotide composition and obviates the need for knowledge of codon boundaries. In addition to being applicable to individual genes, the method can be easily extended to the case of clusters of horizontally transferred genes. With the help of an extensive and carefully designed set of experiments on 123 archaeal and bacterial genomes, we demonstrate that the new method exhibits significant improvement in sensitivity when compared to previously published approaches. In fact, it achieves an average relative improvement across genomes of between 11 and 41% compared to the Codon Adaptation Index method in distinguishing native from foreign genes. Our method's horizontal gene transfer predictions for 123 microbial genomes are available online at http://cbcsrv.watson.ibm.com/HGT/.

INTRODUCTION

As early as 1944, scientists began accumulating experimental evidence on the ability of microbes to uptake ‘naked’ DNA from their environment and incorporate it into their genome (1). Several years later, in 1959, plasmids carrying antibiotic resistance genes were shown to spread among various bacterial species. And as the twentieth century came to a close, there was increased appreciation of the fact that genes found in mitochondria and chloroplasts are often incorporated in the nuclear genome of their host organism (2–4). Nonetheless, there have been intense debates through the years on the possibility that the transfer of genetic material among different species may play a significant role in evolution. This process is known as horizontal gene transfer (HGT) or, equivalently, lateral gene transfer (LGT).

Before the advent of the genomics era, only a handful of horizontal gene transfer events were documented in the literature (5). And even though it had been argued that gene acquisition from foreign species could potentially have a great impact on evolution (6), it was not until after the genomic sequences of numerous prokaryotic and eukaryotic organisms became publicly available that the traditional tree-based evolutionary model was seriously challenged, considering even the possibility of substantial gene exchange (7,8). In particular, it was first observed that some Escherichia coli genes exhibit codon frequencies that deviate significantly from those of the majority of its genes (9). Also, the genomes of Aquifex aeolicus and Thermotoga maritima, two hyperthermophilic bacteria, supported the hypothesis of a massive gene transfer from archaeal organisms with which they shared the same lifestyle (10,11).

Subsequent phylogenetic studies at a genomic scale have demonstrated that the archaeal proteins can be categorized into two distinct groups with bacterial and eukaryotic homologues (12–14). The latter comprise the so-called informational genes (involved in translation, transcription and replication), and their existence can be explained in the context of the model of early evolution which dictates that eukaryotes and archaea descended from a common ancestor, whereas the former appear to be the result of numerous gene transfers among archaea and bacteria.

The significance of horizontal gene transfer goes beyond helping interpret phylogenetic incongruencies in the evolutionary history of genes. In fact, there is strong evidence that pathogenic bacteria can develop multi-drug resistance simply by acquiring antibiotic resistance genes from other bacteria (15,16). More evidence of gene transfer as well as a detailed description of the underlying biological mechanisms can be found in (17). And in (18), the authors present a quantitative estimate of this phenomenon in prokaryotes and propose a classification comprising two distinct types of horizontal gene transfer.

Over time, a number of methods were devised for the identification of horizontally acquired genes. Traditionally, phylogenetic methods have been used to prove that a gene has been horizontally transferred (19). These methods work well when sufficient amounts of data are available for building trees with good support; but very frequently this is not the case and other approaches need to be exploited in order to identify horizontally transferred genes in the genome under consideration. Examples of such approaches include the unexpected ranking of sequence similarity among homologs where genes from a particular organism show the strongest similarity to a homolog from a distant taxon (18), gene order conservation in operons from distant taxa (20,21), and atypical nucleotide composition (22).

Many of the previously published methods for horizontal gene transfer detection were based on gene content and operated under the assumption that in a given organism, there exist compositional features that remain relatively constant across its genomic sequence. Genes that display atypical nucleotide composition compared to the prevalent compositional features of their containing genome are likely to have been acquired through a horizontal process. Consequently, over the years, a number of features have been proposed for defining ‘signatures’ that would be characteristic for a genome: any gene deviating from the signature can be marked as a horizontal transfer candidate. We continue with a brief summary of the various signatures that have been discussed in the literature.

The simplest and historically earliest type of proposed genomic signature is a genome's composition in terms of the bases G and C, known as the genome's G + C content (22). It is important to note that due to the periodicity of the DNA code, as this periodicity is implied by the organization of the coding regions into codons, the G + C content varies significantly as a function of the position within the codon. As a result, four discrete G + C content signatures can be identified. The first corresponds to the overall G + C content and is computed by considering all of the nucleotides in a genome. Each of the remaining three signatures, denoted by G + C(k), with k = 1,2,3, corresponds to the value of the G + C content as the latter is determined by considering only those nucleotides occupying the kth position within each codon; unlike the G + C signature which is computed across all genomic positions, only coding regions are used in the computation of G + C(k).

A related variation of the G + C(k) content idea is the so-called Codon Adaptation Index (CAI) which was introduced in (23). CAI measures the degree of correlation between a given gene's codon usage and the codon usage that is deduced by considering only highly expressed genes from the organism under consideration.

In yet another variation introduced in the context of a study of the E.coli genome, Lawrence and Ochman (24) identified atypical protein coding regions by simultaneously combining G + C (1) and G + C (3). Moreover, and for each gene in turn, they computed a ‘codon usage’ that assessed the degree of bias in the use of synonymous codons compared to what was expected from each of the three G + C(k) values. A gene was rendered atypical when its relative ‘codon usage’, as defined above, differed significantly from its CAI value.

The codon usage patterns in E.coli were also investigated by Karlin et al. in (25) who found that the codon biases observed in ribosomal proteins deviate the most from the biases of the average E.coli gene. Using this observation, they defined ‘alien’ genes as those genes whose codon bias was high relative to the one observed in ribosomal proteins and also exceeded a threshold when compared to that of the average gene.

Another popular genomic signature is the relative abundance of dinucleotides compared to single nucleotide composition. Despite the fact that genomic sequences display various kinds of internal heterogeneity including G + C content variation, coding versus non-coding, mobile insertion sequences, etc., they nonetheless preserve an approximately constant distribution of dinucleotide relative-abundance values, when calculated over non-overlapping 50-kb-wide windows covering the genome; this observation was demonstrated by Karlin et al. in (26,27). But more importantly, the dinucleotide relative-abundance values of different sequence samples of DNA from the same or from closely related organisms are generally much more similar to each other than they are to sequence samples from other organisms. In related work, Karlin and co-workers introduced the ‘codon signature’, which was defined as the dinucleotide relative abundances at the distinct codon positions 1–2, 2–3 and 3–4 (4 = 1 of the next codon) (28): for large collections of genes (50 or more), they showed that this codon signature is essentially invariant, in a manner analogous to the genome signature.

A genomic signature comprising higher-order nucleotides was proposed by Pride and Blaser in (29), where the observed frequencies of all n-sized oligonucleotides in a gene are contrasted against their expected frequencies estimated by the observed frequencies of (n − 1)-sized oligonucleotides in the host genome. In the accompanying analysis, the authors focused on identifying horizontally transferred genes in Helicobacter pylori, and for that genome they showed that signatures based on tetranucleotides exhibit the best performance, whereas higher-order oligonucleotides did not result in any improvement. However, since their analysis was based on a single genome, it is not possible to deduce any generally applicable guidelines.

Hooper and Berg (30) propose as a genomic signature the dinucleotide composed of the nucleotide in the third codon position and the first position nucleotide of the following codon. [This is effectively the 3–4 signature from (28).] Using the 16 possible dinucleotide combinations, they calculate how well individual genes conform to the computed mean dinucleotide frequencies of the genome to which they belong. Mahalanobis distance, instead of Euclidean, is used to generate a distance measure on the dinucleotide distribution. It was also found that genes from different genomes could be separated with a high degree of accuracy using the same distance.

Sandberg et al. investigated the possibility of predicting the genome of origin for a specific genomic sequence based on the differences in oligonucleotide frequency between bacterial genomes (31). To this end, they developed a naïve Bayesian classifier and systematically analyzed 28 eubacterial and archaeal genomes, and concluded that sequences as short as 400 bases could be correctly classified with an accuracy of 85%. Using this classifier, they demonstrated that they could identify horizontal transfers from Haemophilus influenzae to Neisseria meningitis.

Hayes and Borodovsky demonstrated the connection between gene prediction and atypical gene detection in (32). Working with bacterial species, they addressed the problem of accurate statistical modeling of DNA sequences and observed that more than one statistical model were needed to describe the protein-coding regions. This was the result of diverse oligonucleotide compositions among the protein-coding genes and in particular of the variety of their codon usage strategies. In the simplest case, two models sufficed, one capturing typical and the other atypical genes. Clearly, the latter model also allowed the identification of good horizontal transfer candidates. Along similar lines, Nakamura et al. (33) recently conducted a study of biological functions of horizontally transferred genes in prokaryotic genomes. Their work did not introduce a new computational method, but rather applied anew the method originally introduced by Borodovksi and McIninch (34) in the context of gene finding. In a manner analogous to deciding whether a given open reading frame (ORF) corresponds to a gene, Nakamura et al. determined whether a given gene was horizontally transferred and compiled, and reported results for a total of 116 complete genomes.

In (35), the authors identified horizontal gene transfer candidates by combining multiple identification methods. Their analysis is based on a hybrid signature that includes G + C and G + C(k) content, codon usage, amino-acid usage and gene position. Genes whose G + C content significantly deviates from the mean G + C content of the organism are candidate gene transfers provided they also satisfy the following constraints: (i) they have an unusual codon usage (computed in a similar way); (ii) their length exceeds 300 bp; and (iii) their amino-acid composition deviates from the average amino-acid composition of the genome. However, the authors stressed the need to exclude highly expressed genes from the set of candidate transfers: such genes may deviate from the mean values of codon usage simply because of a need to adapt so as to reflect changes in tRNA abundance. As an example, ribosomal proteins are filtered out and are not included in the list of predictions. Similar in flavor, the method described in (36) applies several approaches simultaneously, e.g. G + C content, codon and amino-acid usage, and generates results for 88 complete bacterial and archaeal genomes. The putative horizontally transferred genes are collected and presented in the HGT-DB database that is accessible on-line.

It is important to note that the methods in (35) and (36) do not introduce a new genomic representation scheme, but rather combine several distinct modalities into one feature vector. As is always the case with feature vectors comprising distinct and non-uniform features, it is difficult to derive a distance function that properly takes into account the different units, the different ranges of values, etc. Notably, and in direct contrast to this approach, our proposed method which is outlined below uses a single feature in order to determine whether a gene is indigenous to a genome or not.

In (37), surrogate methods for detecting lateral gene transfer are defined as those that do not require inference of phylogenetic trees. Four such methods were used to process the genome of E.coli K12. Only two of these methods detect the same ORFs more frequently than expected by chance, whereas several intersections contain many fewer ORFs than expected.

Finally, we should mention an approach that is radically distinct from the ones described above. Ragan and Charlebois (38) organize ORFs from different genomes in groups of high sequence similarity (using gapped BLAST) and look at the distributional profile of each group across the genomes. Those ORFs whose distribution profile cannot be reconciled parsimoniously with a tree-like descent and loss are likely instances of horizontal gene transfer. In other words, instead of deciding whether a gene is typical or atypical by comparing its composition to that of the containing genome, they perform a statistical comparison of similar genes across genomes.

In what follows, we present a novel methodology that exploits genomic composition to discover putative horizontal transfers. Notably, our method does not require knowledge of codon boundaries. By carrying out a very extensive set of experiments with 123 archaeal and bacterial genomes, we demonstrate that our method significantly outperforms previously published approaches including the Codon Adaptation Index (CAI), C + G and all its variants as well as methods based on dinucleotide frequencies.

MATERIALS AND METHODS

In this section, we present and discuss our method for deriving generalized compositional features (single modality).

Generalized compositional features

Our proposed approach extends and generalizes composition-based methods in three distinct ways:

• First, we advocate the use of higher-order nucleotide sequences (templates) so as to overcome the diminished discrimination power exhibited by the previously proposed di- and trinucleotide models. Our use of richer compositional features is expected to lead to an increased ability in identifying genes with atypical compositions and thus an improved ability to classify.

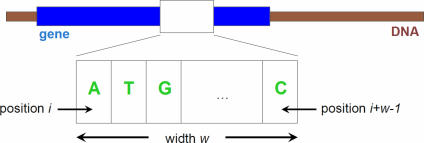
• Second, we extend the composition-based model in a manner that allows us to ‘ignore’ certain nucleotide positions; this is achieved through the use of generating templates that include ‘gaps’ and thus do not comprise consecutive nucleotides. Gaps are indicated with the help of a ‘dot’ or ‘don't care’ character: any nucleotide that occupies the ‘don't care’ position will be ignored during the computation of the signature. As an example, the template A.G will match any of AAG, ACG, AGG or ATG, while ignoring the identity of the nucleotide occupying the middle position.

• Third, we optionally take into account the periodicity of the DNA code; in particular, when collecting the instances of a template, we can impose the constraint that a template be position-specific. For example, when calculating the codon frequencies, the trinucleotide templates to be considered are only the ones that start at positions 3k + 1, where k is a non-negative integer.

In our augmented model, let us denote the compositional feature vector for any given DNA sequence s over a set of templates π = {π₁, π₂,…, π_q} as φ(s) = (α₁, α₂,…, α_q); here α_i is the frequency of template π_i in sequence s.

Instead of using the absolute template frequencies, we may choose to normalize these frequencies over the expected template frequencies: the latter can be derived from the single nucleotide composition with respect to some background reference sequence under the assumption of an i.i.d. model. Typically, if the sequence of interest is a gene g, or a DNA fragment belonging to a genome G, the single nucleotide frequencies of genome G ought to also reflect the expected single nucleotide frequencies of an endogenous gene g. The relative (normalized) frequencies are thus given by the following equation:

$${\alpha }_i=\frac{P_g\left({\pi }_i\right)}{{\prod }_{j=1}^{\left|{\pi }_i\right|}{P}_G\left({\pi }_{ij}\right)},$$

where π_ij is the jth nucleotide of template π_i, P_g(π_i) is the observed frequency of template π_i in gene g ∈ G, whereas the single nucleotide probabilities P_G(π_ij) in the denominator are computed from the entire genome G, and we can choose to make them position-specific or not. The probability of the ‘dot’ character is one.

From compositional features to gene typicality scores

Given a genome sequence, our ultimate objective is to characterize the genes in the genome in terms of how ‘atypical’ they are. Under the assumption that any given genome exhibits a relatively constant composition over intervals that may not be contiguous, genes whose template composition differs substantially from the typical composition of their host genome are likely to have been acquired through a horizontal transfer event. In our work, we assign a ‘typicality’ score S_G(g) to each gene g of genome G: the higher the score the more typical the gene is for the genome. Consequently, genes with low scores will correspond to gene transfer candidates.

A straightforward approach towards the computation of a gene's typicality score given its feature vector φ(g) is to compare it to the feature vector φ(G) for the whole genome. The comparison can be performed in many different ways and it will yield a score that gauges the similarity between the gene in question and the genome as a whole. Five commonly used similarity measures are correlation, covariance, χ² test, Mahalanobis distance and relative entropy.

The first method involves the calculation of the classic Pearson correlation between the gene and genome vectors. In this case, the gene's typicality score S_G(g) within the ‘context’ of genome G can be written as:

$$S_G\left(g\right)=\frac{{\displaystyle \sum _{k=1}^m}\left({\phi }_k\left(g\right)-{\mu }_{\phi \left(g\right)}\right)·\left({\phi }_k\left(G\right)-{\mu }_{\phi \left(G\right)}\right)}{m{\sigma }_{\phi \left(g\right)}{\sigma }_{\phi \left(G\right)}}.$$

Very similar to the correlation measure is the covariance of two vectors:

$$S_G\left(g\right)=\frac{1}{m}{\displaystyle \sum _{k=1}^m}{\phi }_k\left(g\right)·{\phi }_k\left(G\right).$$

The standard χ² test measures the deviation of a vector from its expected value by summing up the deviations of each vector component. In this case, the gene score is obtained by negating the χ² score, so that high χ² values (and thus high deviations) will correspond to low and, thus, atypical gene scores:

$$S_G\left(g\right)=-{\displaystyle \sum _k}\frac{{\left({\phi }_k\left(g\right)-E\left[{\phi }_k\left(g\right)\right]\right)}^2}{E\left[{\phi }_k\left(g\right)\right]}.$$

Here, the expected value for component k is estimated by the mean value of the component across all n_G genes in the genome:

$$E\left[{\phi }_k\left(g\right)\right]=\frac{1}{{\text{n}}_{\text{G}}}{\displaystyle \sum _{g\in G}}{\phi }_k\left(g\right).$$

The need to use the Mahalanobis distance arises in the case where the selected compositional features are significantly correlated with each other, and as a result their covariance matrix K contains important information. Their score is obtained by negating the corresponding Mahalanobis distance, so that high distance values will correspond to low and, thus, atypical gene scores:

$$S_G\left(g\right)=-{\left(\phi \left(g\right)-\phi \left(G\right)\right)}^T{K}^{-1}\left(\phi \left(g\right)-\phi \left(G\right)\right).$$

In the case where the feature vector defines a probability distribution (e.g. all trinucleotides), we can assign a score to each gene by measuring the distance of the distribution defined by the gene vector from the one defined by the genome vector using the concept of relative entropy (also known as Kullback–Leibler distance):

$$S_G\left(g\right)=-{\displaystyle \sum _k}{\phi }_k\left(g\right)ln\frac{{\phi }_k\left(g\right)}{{\phi }_k\left(G\right)}.$$

Again the gene score is obtained by negating the distance value, so that high distance values will correspond to low, hence atypical gene scores.

Our proposed algorithm, Wn, for HGT detection: individual genes

Here we describe in detail our proposed algorithm. Given any genome G, the algorithm returns a list of putative horizontal gene transfers. The goal is to first compute a typicality score for each gene in the genome that reflects the similarity of the gene sequence to the whole genome with respect to the selected compositional features.

Through our analysis, we have discovered that for template sizes greater than two, the optimal performance is obtained when we ignore the periodicity of the genetic code (i.e. by ignoring codon boundaries and counting all the templates including those that begin at the second and third codon positions), use no gaps in the templates, and by choosing ‘covariance’ as the similarity measure for computing the final scores. We use Wn to denote our method, where n is greater than two and is equal to the size of the template. An example of a template is shown in Figure 1. It should be stressed here that, allowing representations based on generalized templates comprising both gap and non-gap characters seems to yield no further improvement for the particular set of genomes we experimented with. Nonetheless, we can expect that, as the sequences of more complete genomes become available, the additional flexibility provided by the gapped templates that we introduced in this work has the potential of further improving performance.

Figure 1.

Example of a template.

We observed that the performance of our method increased with the size of the template, reaching a maximum at size 8; increasing the size of the template further resulted in a sharp drop of performance. With respect to the choice of template size, one needs to keep in mind that higher template sizes will result in greater specificity provided of course that the regions of DNA being processed can yield a sufficient percentage of non-zero counts. As a rule of thumb, smaller size templates should be used when individual gene transfers are sought, whereas larger size templates can be chosen when attempting to identify clusters of horizontally transferred genes, which in turn can be done by using the sliding window method described below.

Our proposed algorithm, Wn, for HGT detection: clusters of transferred genes

For completeness, we now describe a modification of the proposed Wn algorithm so that it can be also applied to the problem of detecting clusters of putative gene transfers: instead of computing the feature vectors over individual genes, the computation is now applied on sliding windows that span multiple, neighboring genes. The size of the window is given in terms of the number of genes that it spans and not in terms of a nucleic acid span: the number of genes to be included in the computation is a parameter in this modified version of our algorithm, while n of course still denotes the template size. For each such window, we obtain a score: the score of a given gene within the window is computed as the average of the scores of all of the windows that include the gene in question. In the next section, we discuss the application of our algorithm on the genome of Enterococcus faecalis which contains a known cluster of horizontally transferred genes conferring vancomycin resistance.

Our proposed algorithm, Wn, for HGT detection: automated threshold selection

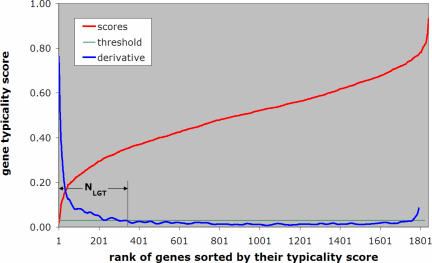
Given the typicality scores that Wn computes for each gene of a genome, we need to be able to automatically determine a threshold value: all genes with scores below it are considered to be horizontal transfers. We illustrate our automated threshold selection methodology with the help of the genome of Aeropyrum pernix. The distribution of the obtained scores f, sorted in order of increasing values, is shown in Figure 2. In the same figure, we also show the derivative f′ of the distribution, properly smoothed by taking the average over sliding windows and normalized so that its values range from zero to one.

Figure 2.

Demonstrating the automatic method for selecting a score threshold using the genome of A.pernix as a test case—see also text.

It can be seen that the scores increase very fast for the first few genes, but once we make the transition from atypical genes to genes of higher typicality, the derivative remains approximately constant. It is precisely at this point that we set the threshold value T on the derivative f′. With the score threshold having been decided automatically, we define the number N_HGT of predicted horizontal gene transfers to be the smallest value i for which the derivative of the ranked scores becomes equal to the threshold T: these N_HGT lowest scoring genes comprise our list of putative gene transfers.

RESULTS

In order to assess the potential of using compositional features in the detection of horizontal gene transfers in a host genome, we designed and carried out a very large number of experiments that simulated gene transfer. The experimental procedure was as follows: we created a pool of donor genes, and randomly sub-selected an appropriate fraction of these genes that were then incorporated into the bacterial or archaeal host genome under consideration. The task at hand is that of recovering as many as possible of the inserted donor genes.

It is important to note that, unlike previously proposed random experiments where artificial genes were produced as random sequences which obeyed some very general statistics (e.g. a given observed mononucleotide frequency distribution), our simulations are carried out using real genes and thus are realistic simulations of what happens in nature (as we currently understand it). Constructing and using random sequences to simulate gene transfers is simply not a valid approach.

We have carried out experiments with two distinct pools of donor genes. The first pool was built from the gene complement of the 27 phages that are shown in Table 1 and comprised 1485 genes. The second pool comprised approximately 350 000 archaeal and bacterial genes and is discussed later in this section. In both sets of experiments, we used as ‘host’ genomes a collection of 123 fully sequenced prokaryotic genomes (archaea and bacteria), which we downloaded from the NCBI/NIH ftp server.

Table 1.

List of phages

Phage	GenBank ID	Genes
Streptococcus thermophilus bacteriophage Sfi21	NC_000872	50
Coliphage alpha3	NC_001330	10
Mycobacterium phage L5	NC_001335	85
Haemophilus phage HP1	NC_001697	42
Methanobacterium phage psiM2	NC_001902	32
Mycoplasma arthritidis bacteriophage MAV1	NC_001942	15
Chlamydia phage 2 virion	NC_002194	8
Methanothermobacter wolfeii prophage psiM100	NC_002628	35
Bacillus phage GA-1 virion	NC_002649	35
Lactococcus lactis bacteriophage TP901-1	NC_002747	56
Streptococcus pneumoniae bacteriophage MM1 provirus	NC_003050	53
Sulfolobus islandicus filamentous virus	NC_003214	72
Bacteriophage PSA	NC_003291	59
Halovirus HF2	NC_003345	114
Cyanophage P60	NC_003390	80
Lactobacillus casei bacteriophage A2 virion	NC_004112	61
Vibrio cholerae O139 fs1 phage	NC_004306	15
Salmonella typhimurium phage ST64B	NC_004313	56
Pseudomonas aeruginosa phage PaP3	NC_004466	71
Streptococcus pyogenes phage 315.4 provirus	NC_004587	64
Staphylococcus aureus phage phi 13 provirus	NC_004617	49
Yersinia pestis phage phiA1122	NC_004777	50
Xanthomonas oryzae bacteriophage Xp10	NC_004902	60
Enterobacteria phage RB69	NC_004928	179
Burkholderia cepacia phage BcepNazgul	NC_005091	75
Ralstonia phage p12J virion	NC_005131	10
Bordetella phage BPP-1	NC_005357	49

Case 1: donor pool comprising phage genes

For each of the 123 host organisms in turn, we conducted k = 100 experiments of simulated transfers from the pool of phage genes into the genome of the host organism. In each case, the number of added genes was chosen to be a fixed percentage of the number of genes in the host genome. The ‘transferred’ genes were selected from the donor pool at random and with replacement. So as to be more realistic, we carried out the simulated-transfer experiment for transfer percentages that ranged between 1% and 8% of the genes in the host genome at hand. For each genome and transfer percentage combination, the task was that of recovering as many of the artificially transferred genes as possible, without using any a priori knowledge about the host genome or the donor genes. For the genome and percentage combination being considered, we accumulated results from over 100 repetitions of the transfer-and-recover experiment and reported the arithmetic average.

In the ideal case, a method ought to be able to recover every single one of the added genes. But the reader should keep in mind that our artificially transferred genes compete with all of the bona fide horizontal transfers, already present in the genome under consideration, for the same top putative transfer positions. Nonetheless, this situation poses no problem for the purposes of simulation as it holds true for all of the tested methods, and thus no method is favored at the expense of another.

Each tested method computes a ‘typicality’ score for each gene based on different gene features each time. Let ρ be the number of genes that we artificially added to the genome being studied: the various methods are evaluated according to their ‘hit ratio’, which is defined as the percentage of artificially added genes occupying the ρ-lowest typicality score values. In other words, we measure how many of the artificial transfers end up occupying the ρ-lowest positions. Clearly, the more successful a method is in discovering gene transfers, the closer the computed hit ratio will be to 100%. If m denotes a gene-scoring method, G is the genome under consideration and $r_i^m\left(G\right)$ is the hit ratio obtained by the method m at the ith iteration of the experiment (with 1 ≤ i ≤ k), then we can define the performance ${\mathrm{Perf}}_G^m$ of method m on genome G as the ‘average of the hit ratios’ that we observed across the k experiments:

$${\mathrm{Perf}}_G^m=\frac{1}{k}{\displaystyle \sum _{i=1}^k}{r}_i^m\left(G\right).$$

Similarly, we define the ‘overall performance’ Perf^m of method m as its average performance across all N organisms:

$${\mathrm{Perf}}^m=\frac{1}{N}{\displaystyle \sum _G}{\mathrm{Perf}}_m^G.$$

We experimented with numerous methods, based on different compositional features and similarity measures and computed the overall feature-based typicality of the genes. In Table 2, we provide a summary of the methods that we have discussed here: four of the methods have appeared previously in the literature whereas the fifth one is Wn, the method we propose and discussed in this manuscript.

Table 2.

Gene scoring methods

Name	Width	Step	Measure	Description
CG	1	1	χ2	G + C content
3/4	2	3	χ2	Dinucleotide composition of codon positions 3 and 1
CODONS	3	3	χ2	Codon composition
CAI	3	3	N/A	Codon Adaptation Index
W8	8	1	Covariance	8-nucleotide composition (no gaps)

Each of the five methods computes a score for each gene according to the method's rules. The Codon Adaptation Index (CAI) is computed and assigned to each gene as its score. The lower this score is the more atypical the gene is considered to be, and its synonymous codon composition deviates from the one observed in its genome. The CAI value for gene g in genome G is given by the following formula:

$$\text{CAI}\left(g\right)=exp\left({\displaystyle \sum _i}{f}_{i}ln{w}_i\right)$$

where f_i is the relative frequency of codon i in the coding sequence, and w_i the ratio of the frequency of codon i to the frequency of the major codon for the same amino acid in the whole genome. In the CG method, the G + C content for each gene is computed and compared against the G + C content of the genome using the χ² test and the χ² value is negated in order to yield the gene typicality score. The third method is based on the composition of the dinucleotides formed by the third position of codon j and the first position of codon j + 1. As before, the χ² test is used to compute the gene scores. CODONS uses the χ² test and W8 covariance as the similarity measures and templates of size 3 and 8 respectively to form their compositional features: in the case of CODONS, only the trinucleotides that correspond to codons are used in the calculation; however, in the case of W8, we count all 8 nt templates without observing codon boundaries.

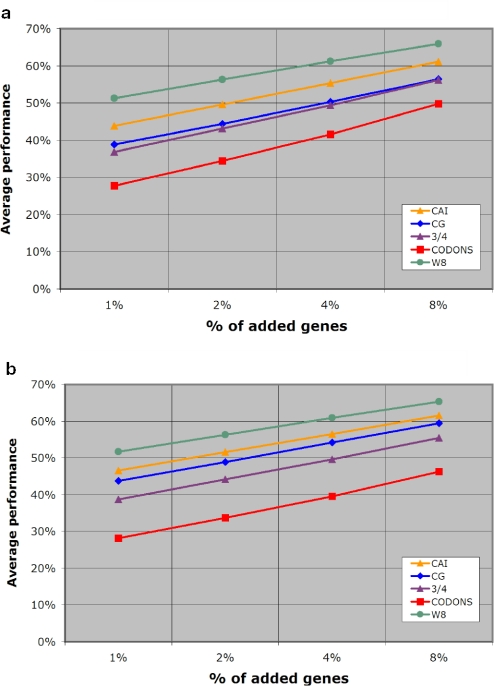
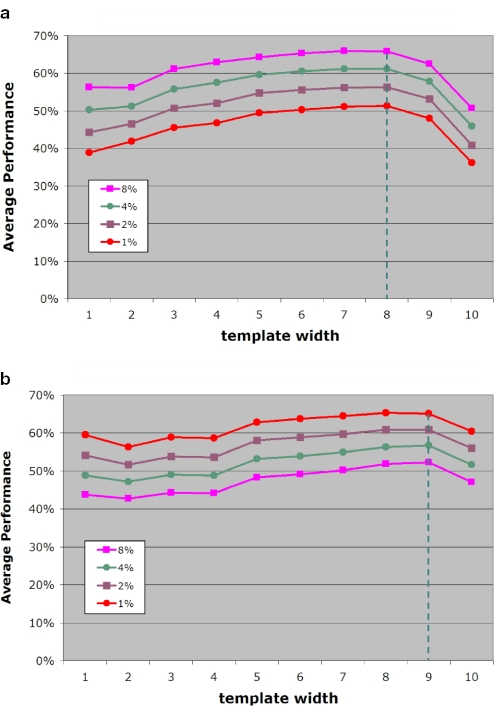
In Table 3, we list the overall performance Perf^m of all five methods for different percentages of artificially added genes. Notably, across all percentages of added genes, our W8 method outperforms the rest. The entries of Table 3 are also shown in Figure 3a in the form of a plot.

Table 3.

Overall performance Perf^m for the methods under evaluation

%HGT	CG (%)	3/4 (%)	CODONS (%)	CAI (%)	W8 (%)
1	38.81	36.80	27.68	43.83	51.28
2	44.41	43.08	34.41	49.58	56.26
4	50.33	49.34	41.59	55.30	61.21
8	56.41	56.24	49.79	61.11	65.88

Figure 3.

Overall performance Perf^m of five scoring methods that has been averaged over 123 genomes: (a) case of a phage donor gene pool and (b) case of a prokaryote donor gene pool.

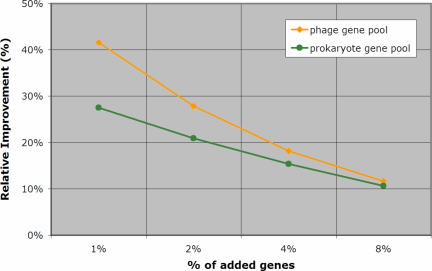
Table 4 shows the improvement achieved by our method when compared to the remaining four methods: the improvement is shown both in absolute percentage points (Table 4A) and in terms of relative values (Table 4B), and represents the average across the 100 experiments that we carried out with each genome and amount of artificial transfers. The data in Table 4B is also depicted graphically in Figure 4. The amount of relative improvement that W8 achieves relative to method m is computed as the average increase in the number of artificially transferred genes that our method detects:

$${\mathrm{Rel}}^m=\frac{1}{N}{\displaystyle \sum _G}{\mathrm{Rel}}_G^m=\frac{1}{N}{\displaystyle \sum _G}\frac{{\mathrm{Perf}}^{W8}\left(G\right)-{\mathrm{Perf}}^m\left(G\right)}{{\mathrm{Perf}}^m\left(G\right)}$$

and is a measure of how many more horizontal transfers are detected by W8. For example, in the experiments with 2% added genes from the prokaryotic pool, our method discovered 27% (respectively 70%) more artificial transfers than CAI (respectively CG).

Table 4.

Improvement of reported W8 method over previous methods

%HGT	W8 vs CG (%)	W8 vs 3/4 (%)	W8 vs CODONS (%)	W8 vs CAI (%)
(A) % improvement in overall performance
1	12.47	14.48	23.60	7.45
2	11.85	13.18	21.85	6.68
4	10.88	11.87	19.62	5.91
8	9.47	9.64	16.09	4.77
(B) % average relative improvement
1	146.57	93.01	232.79	41.61
2	70.57	59.82	129.98	27.87
4	32.90	37.24	78.96	18.18
8	19.88	22.04	45.05	11.64

Figure 4.

Achieved relative improvement Rel^CAI of W8 versus CAI averaged over all experiments and all genomes (see also text).

It is worth pointing out that our method outperforms CAI across all amounts of artificial insertions with which we have experimented, and exhibits significant relative improvements that range between 11% and 41%. Equally important is the fact that our method exhibits much greater sensitivity and shows a very significant advantage over all of the earlier methods when the number of horizontally transferred genes is small compared to the number of genes in the host genome.

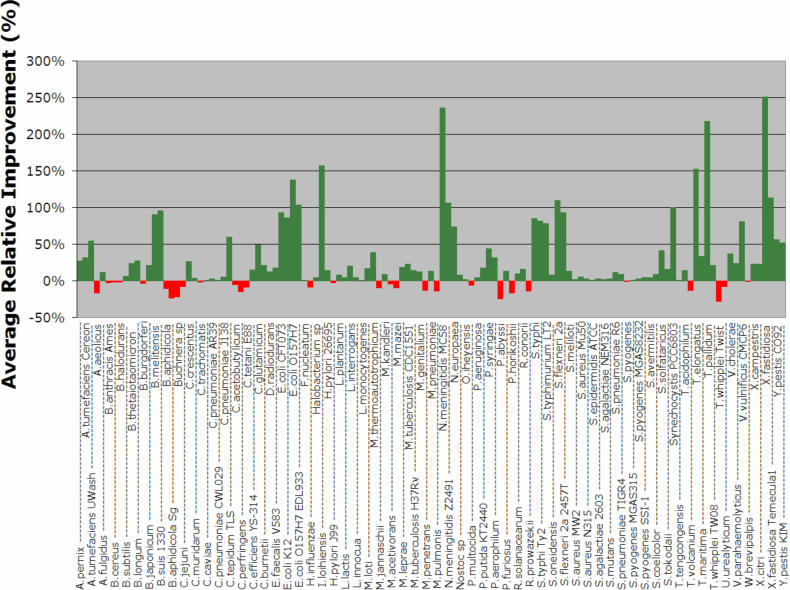
Figure 5 shows a detailed analysis of the performance of W8 compared to the CAI method for each of the 123 genomes and for those experiments where we added 2% donor genes. In this figure, we use green-colored bars for those genomes in which W8 outperforms CAI, and a red-colored bar if the opposite holds true. The height of each bar shows the magnitude of the relative improvement ${\mathrm{Rel}}_G^m$ achieved by our method over CAI as an average over the 100 experiments and can be either positive (green bars) or negative (red bars). As can be seen here, for the majority of the organisms (91 versus 32), the W8 method recovers more of the artificially inserted genes than CAI does. But more importantly, W8 does so while achieving a significantly higher relative improvement margins than CAI. The performance of our W8 method on each genome (both average and SD) can be found in the Supplementary Figure 1.

Figure 5.

Average relative improvement ${\mathrm{Rel}}_G^{\mathrm{CAI}}$ of W8 over CAI for each one of the 123 organisms. Each point is an average over 100 experiments with donor genes drawn from the phage gene pool (see also text).

Next, we exhaustively studied the impact that the size of the template has on the overall performance. Using the same experimental protocol as above and carrying out 100 experiments per organism, we observed that for template sizes greater than 2, the optimal performance is achieved when we ignore codon boundaries and use covariance to compute the similarity scores. Figure 7a shows atypical gene detection performance as a function of the employed template size. It is evident from this figure that an increase in template size leads to continuous increase in performance reaching a maximum for template sizes between 6 and 8 inclusive. In fact, the performance is nearly identical for these three template sizes. Any further increase in the template size leads to a quick drop in performance.

Figure 7.

Achieved overall performance Perf^m as a function of template size and for different percentages of artificially added genes: (a) case of phage gene donor pool and (b) case of prokaryotic gene donor pool.

Case 2: donor pool comprising genes from archaeal and bacterial genomes

We also repeated the above experiments but this time the pool from which the donor genes were selected comprised the approximately 350 000 genes from the 123 genomes that we used as hosts. In other words, we effectively simulated the case where our host genomes could exchange genes with one another in any conceivable combination. To the best of our knowledge, this kind of simulation has not been previously used in the context of evaluating a horizontal gene transfer method. Naturally, we added a bookkeeping stage in this simulation that ensured that all the genes that were artificially inserted in genome G originated in genomes other than G.

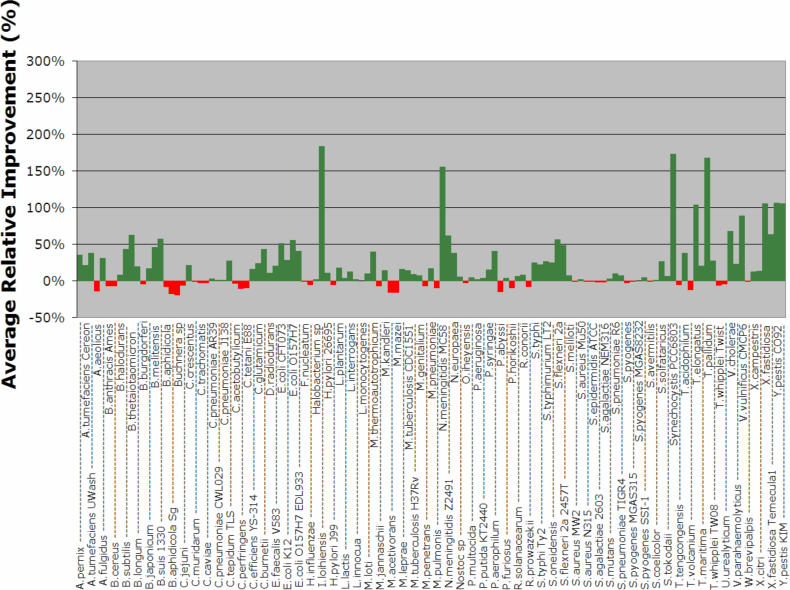
In order to account for the bigger size of the donor pool, we conducted k = 1000 repetitions for each artificial transfer experiment. In Figure 3b, we show the overall performance of the five evaluated methods as a function of the percentage of added genes, and in Figure 6 we plot the relative improvement achieved in each genome by our method compared to CAI. The performance of our W8 method on each genome (both average and SD) can be found in the Supplementary Figure 2. Finally, the effect that changing the template size has on performance is shown in Figure 7b. Not surprisingly, the results obtained during the simulation with the prokaryotic donor pool are in agreement with those obtained from the simulation with the phage donor gene pool.

Figure 6.

Average relative improvement ${\mathrm{Rel}}_G^{\mathrm{CAI}}$ of W8 over CAI for each one of the 123 organisms. Each point is an average over 1000 experiments with donor genes drawn from the prokaryote gene pool (see also text).

There still remains the issue of which of the three best-performing template sizes to use. This depends on the expected size of the DNA fragment that will be processed. Given that the sensitivity achieved by template sizes 6 through 8 is virtually the same, use of the largest possible template size will allow us to achieve greater specificity, provided of course that the regions of DNA under consideration can generate a substantial number of non-zero counts. As a rule of thumb, we propose that smaller template sizes be used when isolated gene transfers are sought. Larger size templates will be more appropriate when attempting to identify clusters of horizontally transferred genes.

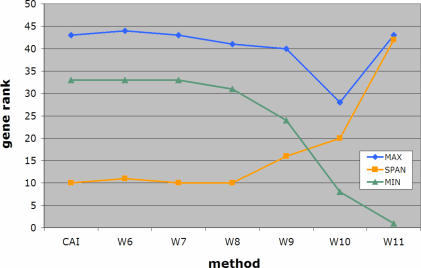
We conclude by applying the sliding-window version of our algorithm to the genome of E.faecalis, where a cluster of vancomycin-resistance related genes is known to have been horizontally transferred. As a matter of fact, in E.faecalis V583, there is a cluster of seven genes, EF2293–EF2299, that confers vancomycin resistance to E.faecalis. Using the sliding window version of our method over windows of five consecutive genes, and template sizes that ranged from 6 through 11 inclusive, we computed scores for each of E.faecalis' genes. CAI values were also generated for the same gene collection. Our goal was to compare the atypicality ranks of the genes that are known to be horizontal transfers as these ranks would be deduced by each of five scoring methods. As stated above, the lower the score of a gene (equivalently: the lower the gene's rank), the more atypical it is considered to be. Given the cluster's common origin, the ideal method should be able to report this collection as a group with no other genes achieving atypicality scores within the range of values spanned by the cluster's genes. Moreover, the ideal method should be able to assign as low scores as possible to this collection emphasizing its horizontally transferred nature. In Figure 8, we show the results of the gene ranks produced by some of the methods. As can be seen here, W6 through W8 perform equally well. The span of gene ranks for the cluster's members is low for template sizes 6 through 8 and equal to the span obtained by the CAI method. As anticipated, W8 outperforms CAI by reporting the genes of this cluster earlier in the list of putative horizontal transfers—this is indicated by the overall lower rank values which are assigned to the cluster as a whole. Further increasing the specificity of the employed templates by increasing their size results in earlier reporting of the vancomycin cluster in the list of candidate transfers. But this is achieved at the expense of increasingly losing the score coherence, which is expected given that the genes under consideration are part of the same logical unit. This last experiment further corroborates the conclusion reached during our artificial-insertion experiments that a template size of 8 nt (i.e. W8 method) represents an optimal choice for Wn.

Figure 8.

Detecting the vancomycin-resistance cluster of horizontally transferred genes in E.faecalis. In an ideal setting, the genes of this cluster should be reported as a group (i.e. their ranks for a given scoring scheme should be as close to each other as possible) and uninterrupted by genes that do not belong to the cluster. Additionally, the ideal method should be able to report typicality scores for the group as a whole that are as low as possible or, equivalently, assign gene ranks to these genes that are as low as possible (see also text).

DISCUSSION

In this paper, we introduced and discussed a new, composition-based framework for the detection of horizontal gene transfers. Our proposed method, Wn, is based on compositional features but extends and generalizes all previously proposed schemes. Wn works by assigning a typicality score to each gene that reflects the gene's similarity with the containing genome as this is gauged by the features in use. We have also described a way to automatically determine a typicality score threshold. Finally, an extension of Wn for the case where the sought transfers are likely to appear in clusters (as opposed to isolated genes) was also described and discussed. We have created a website comprising the predictions of the horizontal gene transfers for all 123 archaeal and bacterial genomes based on our method at http://cbcsrv.watson.ibm.com/HGT/.

We carried out a comparative evaluation of Wn and previously reported computational methods for the discovery of horizontal gene transfers. In particular, we evaluated five representative methods by inserting random, varying-size collections of phage and prokaryotic genes in each of 123 host genomes (archaea and bacteria) and processing those artificially created genomes with each method. Our objective was to recover in the lowest-scoring positions (highly atypical genes) as many of the added phage genes as possible without making use of any a priori knowledge about either the host organism or the inserted genes. These experiments as well as the study of a specific, documented case from E.faecalis strongly demonstrated that templates with sizes ranging from 6 to 8 nt yield optimal performance.

We also reported on pairwise comparisons of Wn with the CAI and G + C methods and for each of 123 genomes in turn. Combining the results across all 123 genomes, W8 clearly outperformed both CAI and G + C. W8 achieved very significant relative improvements over CAI that averaged 25%. The relative improvements over G + C were even more pronounced.

Arguably, for many years, the essence of computational methods that relied on genomic DNA alone to draw conclusions on horizontal gene transfers had remained largely unchanged. In this light, our proposed method is of particular relevance: it is very fast, it need only access the genomic DNA in question (i.e. partial or whole sequence of host genome and partial or whole sequence of candidate stretch of DNA), it obviates the need for access to databases of genomic sequences, it obviates the need for comparative analyses with other genomes, and finally, it does not make use of any codon boundary knowledge. Despite the minimal amounts of information that our method uses, a very extensive series of computational experiments on 123 genomes amply demonstrated the superiority of our method, which achieved a relative improvement of between 11% and 41% over CAI.

Summarizing, we would like to point out that our method aims at identifying genes that diverge from the typical gene profile—measured in terms of template frequencies—of the genome where they are found. It is known, however, that in addition to horizontally transferred genes with atypical profiles, there exist also native to the organism genes that exhibit atypical characteristics. Classic examples include the ribosomal RNA proteins whose profiles are often relatively atypical: these genes belong to the category of informational genes that are widely believed to have limited mobility and do not tend to transfer across species (39). Consequently, we exclude these genes from our final list of candidate gene transfers. It should be noted however that even informational genes can undergo horizontal transfer, as was recently shown through a phylogenetic analysis of the ribosomal protein S14 (40). Other groups of informational genes such as the aminoacyl-tRNA synthetases, which are essential components of the genome's translation machinery, appear to also undergo horizontal transfer (41–43), but unlike the case of ribosomal proteins, we do not exclude any aminoacyl-tRNA synthetases from our reported results.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.