Thermodynamics of the Flexible Metal-Organic Framework Material MIL-53(Cr) From First Principles

Abstract

We use first-principles density functional theory total energy and linear response phonon calculations to compute the Helmholtz and Gibbs free energy as a function of temperature, pressure, and cell volume in the flexible metal-organic framework material MIL-53(Cr) within the quasiharmonic approximation. GGA and metaGGA calculations were performed, each including empirical van der Waals (vdW) forces under the D2, D3, or D3(BJ) parameterizations. At all temperatures up to 500 K and pressures from −30 MPa to 30 MPa, two minima in the free energy versus volume are found, corresponding to the narrow pore (np) and large pore (lp) structures. Critical positive and negative pressures are identified, beyond which there is only one free energy minimum. While all results overestimated the stability of the np phase relative to the lp phase, the best overall agreement with experiment is found for the metaGGA PBEsol+RTPSS+U+J approach with D3 or D3(BJ) vdW forces. For these parameterizations, the calculated free energy barrier for the np-lp transition is only 3 to 6 kJ per mole of Cr₄(OH)₄(C₈H₄O₄)₄.

Microporous flexible metal-organic framework materials are fascinating both from a fundamental point of view and for their numerous potential applications such as gas storage, gas separation, sensors, drug delivery, etc.[1–5] A well-studied example is the MIL-53 family,[6] with formula M(OH)(C₈H₄O₄), where is M is a trivalent species such as Cr, Sc, Al, Ga or Fe. These structures consist of zigzag M-OH-M-OH… chains, crosslinked by 1,4-benzodicarboxylate O₂C-C₆H₄-CO₂ (bdc) units (Fig. 1). Each M is coordinated by two oxygens of OH units and four carboxylate oxygens yielding octahedral oxygen coordination.

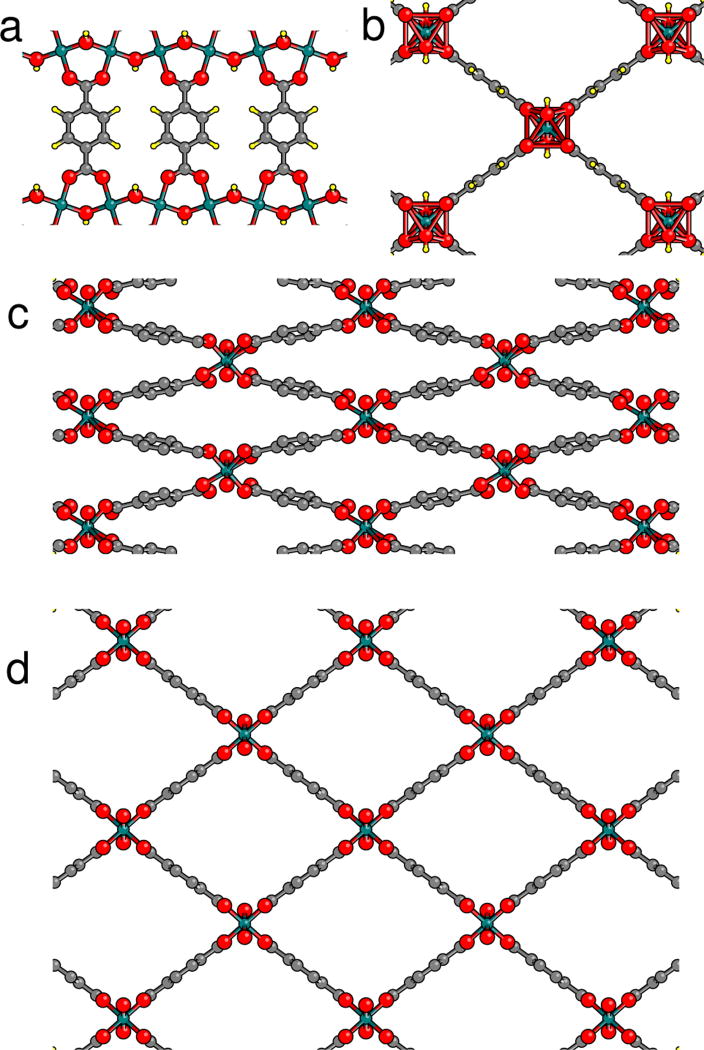
FIG. 1.

Structure of MIL-53(Cr). Cr atoms green, O red, C gray, and H yellow. (a) bdc linkers joining zigzag Cr-OH-Cr-… chains. (b) Each zigzag chain is coordinated with four neighboring chains; each Cr is octahedrally coordinated with six O. (c) Narrow pore (np) phase showing bdc rotations. (d) Large pore (lp) phase. In (c) and (d), the H are not shown.

These MIL-53 compounds exhibit a variety of topologically equivalent structures with different volumes, but generally include a narrow pore (np) structure and a large pore (lp) structure, both with formula M₄(OH)₄(bdc)₄ per conventional unit cell, but with significantly different volumes. In MIL-53(Al), the phase transition between np and lp forms can be reversibly achieved by cycling the temperature;[7] the cell parameter corresponding to the direction of the short axis of the lozenge pores was found to increase by 87 % in the np-lp transformation. By way of comparison, the strain variations achieved or predicted in functional “hard” materials such as (PbMg_1/3Nb_2/3O₃)_(1−x)-(PbTiO₃)_x[8] or BiFeO₃[9] are much smaller. The large hysteresis[7] in the np-lp phase transition of MIL-53(Al) indicates that the transition is first-order. Taking the transition temperature as the midrange of the hysteresis loop, the transition temperature T_c is approximately 260 K; an estimate based on experimental sorption measurements places the transition at a somewhat lower temperature of 203 K.[10]

For empty MIL-53(Cr), the lp structure is thermodynamically preferred at all temperatures. In this system, a phase transition to a np structure has instead been observed in the case of (1) sorption of a variety of sorbates; (2) pressure. The hysteresis of the process in each case[11] indicates again that there is a transition barrier. By fitting sorption isotherms, it was determined that the free energy difference between the lp and np forms of MIL-53(Cr) was only about 12 kJ mol⁻¹ of Cr₄(OH)₄(bdc)₄.[12–14] An experiment that put the system under hydrostatic pressure[15] came up with a similar free energy difference.

The phase transition of MIL-53(Al) was explained by Walker et al.[16] in 2010. Van der Waals interactions stabilize the np structure at low temperature, and vibrational entropy drives the structural transition to the lp phase above T_c. Density functional theory (DFT) phonon calculations were used to quantify the vibrational entropy. In that work, however, the DFT energy and vibrational entropy were determined for only the np and lp structures. However, to build an accurate picture of the np-lp phase transition, including the hysteresis and possible coexistence of np and lp phases,[17] it is necessary to know the quantitative free energy landscape over the full volume range spanning the np and lp structures. This free-energy landscape of MIL-53 systems has previously been modeled in an ad hoc manner.[18, 19] This paper uses density functional total energy and phonon linear response calculations to compute the Helmholtz and Gibbs free energy in MIL-53(Cr) as a function of temperature, pressure, and cell volume, under the quasiharmonic approximation. MIL-53(Cr) was chosen because of its relatively simple phase transformation behavior and because it is well-characterized experimentally.

The thermodynamic calculations are performed within the quasiharmonic approximation. In the quasiharmonic approximation, the anharmonic lattice dynamics that leads to thermal expansion, etc., is approximated by harmonic lattice dynamics where the phonon frequencies are volume-dependent. Suppose that one has a crystal where the rank-ordered frequencies ν_μ(V) can be determined for an arbitrarily large supercell (equivalently at arbitrary points in the Brillouin zone of the primitive cell). The contribution of phonons to the thermodynamics is then given well-known expressions.[20–23] Defining a dimensionless parameter $x_{\mu }(V,T)=\frac{h{\nu }_{\mu }(V)}{k_{B}T}$, the molar internal energy as a function of volume and temperature is given by

$$\frac{U}{N}(V,T)={\text{Lim}}_{|a_{\text{min}}|\to \infty }\frac{1}{N}(U_0(V)+k_{B}T\sum _{\mu =4}^{3N_A}[\frac{x_{\mu }(V,T)}{2}\text{coth}(\frac{x_{\mu }(V,T)}{2})]),$$ (1)

the Helmholtz free energy by

$$\frac{F}{N}(V,T)={\text{Lim}}_{|a_{\text{min}}|\to \infty }\frac{1}{N}(U_0(V)+k_{B}T\sum _{\mu =4}^{3N_A}[\frac{x_{\mu }(V,T)}{2}+\text{ln}(1-e^{-x_{\mu }(V,T)})]),$$ (2)

and the Gibbs free energy is given by $\frac{G}{N}(V,T)=\frac{F}{N}(V,T)+PV$. U₀(V) is the ground state energy neglecting zero-point vibrations, N the number of moles and N_A the number of atoms in the supercell, and the summation begins at μ = 4 to avoid the weak singularity due to the zero-frequency translational modes.

First principles density functional theory calculations, as encoded in the VASP software (24 and 25), were used to compute U₀(V) and ν_μ(V) for a 152-atom supercell of MIL-53(Cr), doubled along c so as to make a, b, and c similar in magnitude for the lp phase. Two different sets of calculations were performed: GGA calculations using the PBEsol functional[26] and meta-GGA calculations using the PBEsol+RTPSS[27] functionals. These functionals were chosen because we have had success with them in past studies of microporous materials.[28, 29] For each level of DFT, the nonlocal van der Waals interactions were treated using three different approximations of Grimme et al.: DFT-D2,[30] DFT-D3,[31] and DFT-D3(BJ).[32] Anisotropic Hubbard parameters[33] were used for Cr and O atoms (GGA: U(Cr) = 4.0 eV, J(Cr) = 0.5 eV; metaGGA: U(Cr) = 2.8 eV, J(Cr) = 0.5 eV; U(O) = 7.05 eV). Spin polarized calculations were performed using the most-stable antiferromagnetic arrangement of charges on the Cr³⁺ ions. Further details of the DFT calculations are given in the Supplementary Information (SI).

Determination of U₀(V) for each functional was done via straightforward fixed-volume relaxation for (primitive cell) increasing in 50 ų steps from 650 ų to 1700 ų. The phonon frequencies for the 152-atom supercell were calculated using ab initio linear response. As this method converges toward exact second derivatives of the energy, it is more accurate than fitting frozen-phonon results. Due to the large number of degrees of freedom, the phonon calculations are very expensive, and eventually only three calculations were used for the thermodynamics: V = 710 ų, V = 1200 ų, and V = 1506 ų. Linear response was only done using GGA and DFT-D2; the same phonon frequencies ν_μ(V) were used for each functional in Eq. (2); only the U₀ changed. Because the variation in volume between the np and lp phases is so large, one does not expect the conventional linear Grüneisen approximation for ν_μ(V) to apply. Instead, we fit the phonon frequencies at intermediate volumes by fitting to the following physically-motivated expression:

$${\nu }_{\mu }^2(V)={\nu }_{\mu \infty }^2+C_1/V+C_2/V^2.$$ (3)

The coefficients in Eq. (3) were determined by fitting the results for the three frequencies calculated. If ${\nu }_{\mu \infty }^2$ in the fit was less than zero, it was set to zero and the fit recalculated. Due to computational limitations, it is not possible to calculate larger supercells for use in Eq. (2). Instead, the contribution of optical phonons to the thermodynamics was approximated by the phonon spectra calculated for the single 152-atom supercell. The contribution of acoustic phonons to the thermodynamics was approximated by numerical integration of estimated acoustic frequencies over the first Brillouin zone. Further details are given in the Supplementary Information.

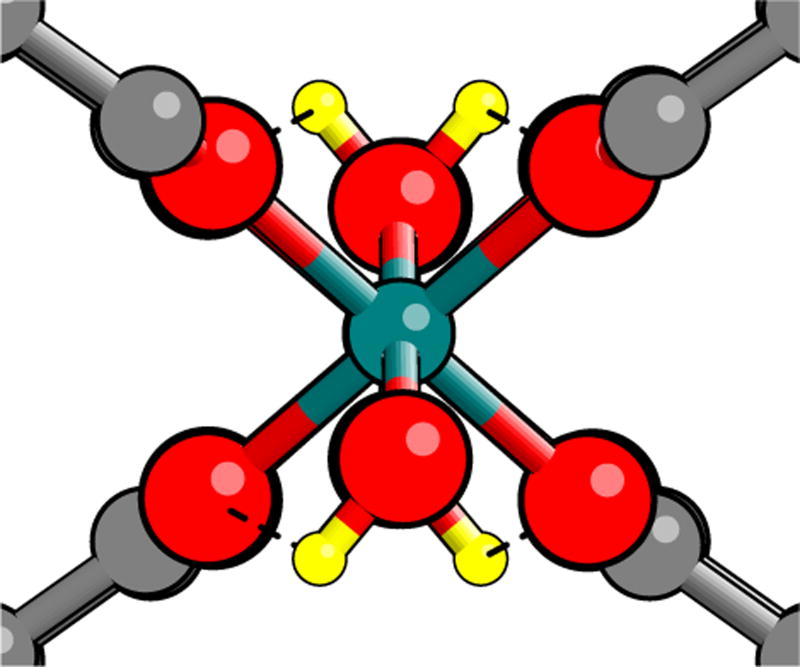
First, the phonons were calculated for the np and lp structures. All modes were stable for the np structure. For the lp structure, instabilities were found. The most unstable modes, for both the force-constant and dynamical matrices, were hydrogen “flopping” modes in which the H in each hydroxyl group move in the ±x direction so as to decrease the distance to a pair of carboxylate oxygens (Fig. 2). Fully relaxing this mode maintains orthorhombic symmetry, the 152-atom cell is now a primitive cell.

FIG. 2.

Local geometry of MIL-53(Cr) (lp) after DFT relaxation of “H flopping” mode. Each H relaxes to sit approximately 2.4 Å from each of a pair of oxygens (dashed lines); the O are superposed from this vantage point.

The structure obtained upon relaxation of the flopping instability was taken as the reference lp structure. To obtain the initial structure for the fixed volume relaxations used to determine U₀(V), the ionic coordinates were interpolated (or extrapolated) from the initial np and lp structures.

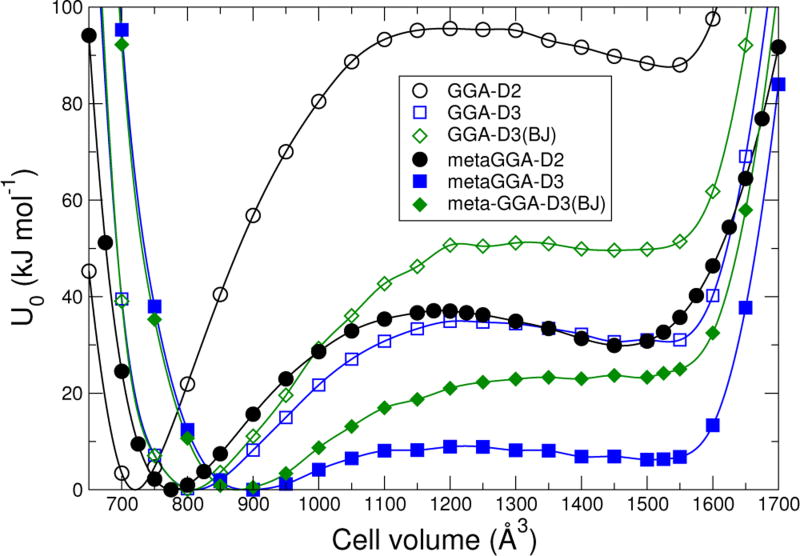
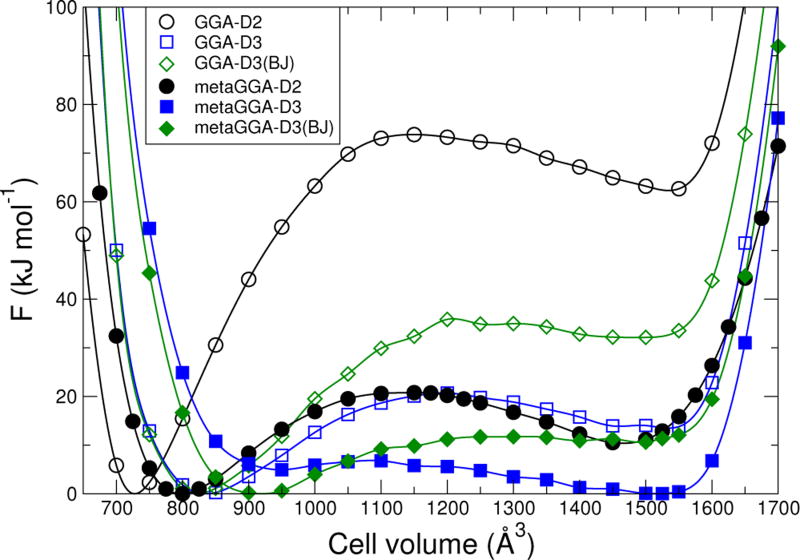
The U₀(V) determined for the various density functionals are shown in Fig. 3. The F(V) for T = 293 K are shown in Fig. 4. For every plot in Fig. 4, there are two minima in the free energy, corresponding to lp and np structures. The effect of phonon entropy is to reduce the free energy of the lp structure with respect to the np structure, as expected. Calculations show that the free energies for temperatures up to 500 K and pressures between −30 MPa and 30 MPa maintain two minima for all density functionals tested.

FIG. 3.

Calculated DFT energy for MIL-53(Cr) at 0 K as a function of volume for different density functionals, neglecting zero-point motion. Each curve is scaled so that its minimum is zero.

FIG. 4.

Calculated Helmholtz free energy for MIL-53(Cr) at 293 K as a function of volume for different density functionals. Each curve is scaled so that its minimum is zero. The effect of atmospheric pressure of about 0.1 MPa is negligible on this scale.

Table I summarizes and compares the results for the different functionals used. The volumes at which the minima for U₀ occur are given by V_0np and V_0lp. The locations of the minima in F at room temperature (RT; 293K) are given by V_np (RT) and V_lp (RT). The calculated difference in F between the np and lp minima is ΔF(RT) = F_lp (RT) − F_np (RT). The critical pressure P_c is where the calculated Gibbs free energy of the np and lp phases becomes equal at T = 293 K. G_b (RT; P_c) is the calculated free energy barrier between the phases at this pressure.

TABLE I.

Calculated structural and thermodynamic results for MIL-53(Cr) for different choices of the density functional. See text for explanation of the column headings. V are in ų; F and G in kJ mol⁻¹ (1 mole = 1 mole of Cr₄(OH)₄(bdc)₄); P in MPa. RT is room temperature, or 293 K.

xc	vdW	V0np	V0lp	Vnp(RT)	Vlp(RT)	ΔF	Pc	Gb(RT; Pc)
GGA	D2	720	1533	728	1534	+62.3	−127.0	45.6
GGA	D3	811	1532	835	1534	+13.5	−32.0	14.1
GGA	D3(BJ)	806	1443	822	1483	+32.1	−76.8	18.7
metaGGA	D2	778	1461	798	1466	+10.4	−25.6	16.0
metaGGA	D3	892	1505	948	1512	−4.9	14.6	3.2
metaGGA	D3(BJ)	875	1393	919	1493	+10.6	−30.7	6.0

Substantial differences are seen depending on what density functional is used. The general trend is for the GGA functionals and the D2 vdW term to give lower V_np and higher ΔF than the metaGGA functionals and D3 or D3(BJ) choices for the vdW interaction. Which functional gives the best agreement with experiment? The experimental unit cell volume of the lp phase of MIL-53(Cr) is 1486 ų.(Ref. 34) The volume of the np phase formed upon sorption of H₂O is 1012 ų,(Ref. 34) but this cannot be directly compared with the calculation for the empty cell reported here. As the np phase of MIL-53(Cr) is thermodynamically unstable experimentally, we take the experimental volume[7, 35] of MIL-53(Al) np, 864 ų, and estimate that the volume of MIL-53(Cr) should be about 900 ų due to the larger ionic radius of Cr³⁺. The best agreement with experiment for the lattice parameters is for the metaGGA-D3(BJ) parameterization, while the second best is for metaGGA-D3. On the other hand, the relative stability of the lp phase found experimentally, ΔF ≈ −12.0 kJ mol⁻¹ is underestimated by all the functionals chosen. The metaGGA-D3 calculation is best in this regard, as it is the only calculation to yield a negative ΔF. All of the metaGGA calculations perform better than GGA in predicting the relative phase stability. As the metaGGA-D3 and metaGGA-D3(BJ) have the best agreement with experiment, their low values of the transition barrier G_b, 3.2 to 6.0 kJ mol⁻¹ should be considered most reliable.

It is interesting to put the comparative results in context of previous studies. In MIL-53, it has previously been found that the D2 vdW overbinds the np phase;[36] this work confirms that result. Benchmarking the performance of DFT calculations is currently receiving a great deal of attention[37–39]. In Ref. 39, over sixty different density functionals are compared. Although the RTPSS functional is not tested, the related metaGGA functional TPSS-D3 gives good results for graphite, which suggests that these parameterizations may work well for MIL-53, where the np phase has benzyl rings of carbon approaching each other. Further work is needed to make a full comparison among methods because the current work: (1) includes Hubbard U and J parameters; (2) needs a vdW functional that reproduces the vdW interactions correctly over a wide range of structural distortion, not merely at one equilibrium point.

The metaGGA-D3 calculation predicts that the lp phase of MIL-53(Cr) is stable at room temperature, in agreement with experiment. Interestingly, it predicts a transition to the np phase below T = 160 K, similar to what actually occurs for MIL-53(Al). The estimated change in ΔF with temperature is about −0.036 kJ mol⁻¹ K⁻¹. Applying this to the experimental ΔF ≈ −12.0 kJ mol⁻¹, the lp phase is expected to remain stable down to T = 0 K, albeit with a free energy advantage of less than 2 kJ mol⁻¹.

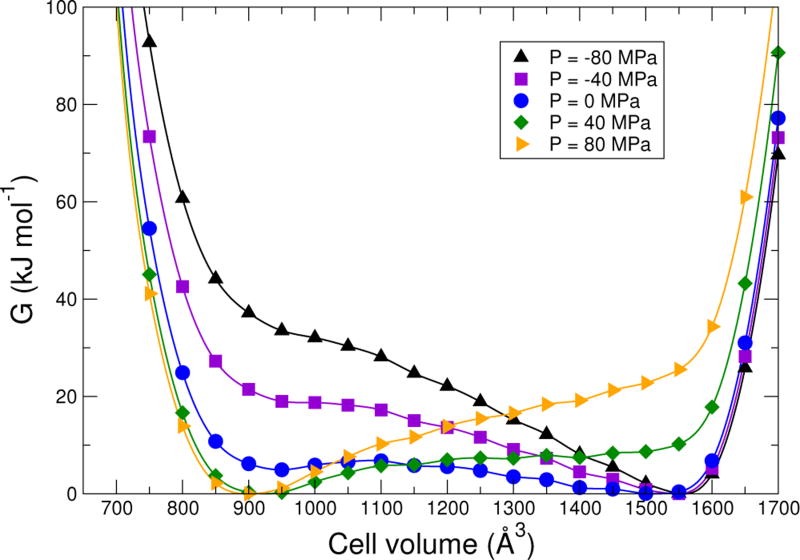
The shallowness of the free energy profile suggests that sufficiently large positive or negative pressure would drive the Gibbs free energy G(V, T = 293 K) into a regime where it has only one minimum corresponding to either a np or a lp structure. In Fig. 5, we show G(V, T = 293 K) for various pressures −80 MPa to 80 MPa, using the metaGGA-D3 results. At pressures above about 60 MPa, there is a unique minimum at the np phase; below about −40 MPa, there is one minimum at the lp phase. If the zero in pressure is shifted to correct for the error in the metaGGA-D3 ΔF with respect to experiment, the predicted pressures are shifted to about 80 MPa and −20 MPa, respectively. Of course the prediction of the pressures at which the free energy converts to a single minimum only sets an upper bound on the width of the pressure hysteresis loop; in practice, fluctuations will cause the transitions to occur at less extreme pressures. With this is mind, experimental transition pressures for the hysteresis loop of roughly 50 MPa and 20 MPa for MIL-53(Cr)[40] are consistent with the DFT results. Note that negative pressures do have physical relevance in microporous materials in the case of sorption-the effective solvation pressure can be either positive or negative depending on the sorbate concentration.[41]

FIG. 5.

Calculated Gibbs free energy for MIL-53(Cr) at 293 K as a function of volume and pressure for the metaGGA-D3 density functional. Each curve is scaled so that its minimum is zero.

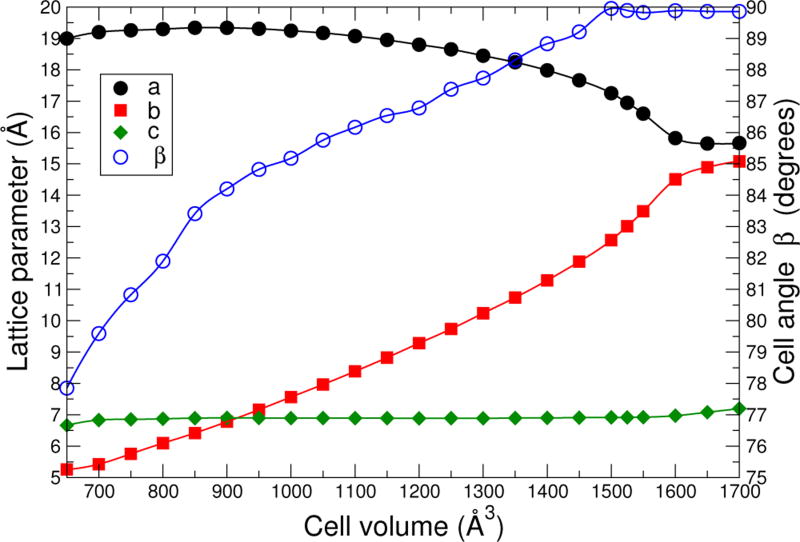
In Fig. 6, the crystallographic data for the DFT metaGGA-D2 structural relaxations are shown. The lattice parameters are scaled to the volume of the conventional unit cells. To make the orthorhombic-monoclinic transition clear, the monoclinic cell parameters a and β are for an unconventional body-center monoclinic setting. The orthorhombic-monoclinic transition occurs at V ~ 1500 ų, intriguingly close to the experimental cell volume. In addition to the structural transitions, there are three regimes in the behavior of the lattice constants: (1) below about 850 ų, a b and c all increase with volume; (2) between about 850 ų and 1650 ų, a decreases with volume b increases with volume, and c is nearly flat as the structure flexes; (3) above about 1650 ų, all lattice parameters increase again. The crossover between regimes (2) and (3) does not occur at the same volume as the monoclinic-orthorhombic transition. To a first approximation, the free energy is nearly flat in regime (2) and increases rapidly above and below this range. The three regimes agree qualitatively with those seen in a recent experiment on the related material MIL-53(Al) under pressure.[42]

FIG. 6.

Calculated MIL-53(Cr) lattice parameters and cell angle β versus volume.

To summarize, we used density functional theory total energy and linear response phonon calculations to compute the free energy profile of MIL-53(Cr) under the quasiharmonic approximation. The density functionals that best match the experimental results give remarkably flat free energy profiles, with a transition barrier of only about a 3 to 6 kJ mol⁻¹ between the the narrow pore and large pore phases.

I thank Laura Espinal, Kevin F. Garrity, and Winnie Wong-Ng for helpful discussions.