Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet

Quanta of collective spin excitations are observed in a ferromagnet by measurements of a superconducting quantum bit.

Abstract

Combining different physical systems in hybrid quantum circuits opens up novel possibilities for quantum technologies. In quantum magnonics, quanta of collective excitation modes in a ferromagnet, called magnons, interact coherently with qubits to access quantum phenomena of magnonics. We use this architecture to probe the quanta of collective spin excitations in a millimeter-sized ferromagnetic crystal. More specifically, we resolve magnon number states through spectroscopic measurements of a superconducting qubit with the hybrid system in the strong dispersive regime. This enables us to detect a change in the magnetic moment of the ferromagnet equivalent to a single spin flipped among more than 10¹⁹ spins. Our demonstration highlights the strength of hybrid quantum systems to provide powerful tools for quantum sensing and quantum information processing.

INTRODUCTION

Engineering interactions between photons and quanta of excitations in atomic and solid-state systems are central to the development of quantum technologies. Cavity and circuit quantum electrodynamics have enabled the realization of many gedanken experiments in quantum optics (1–3), as well as offering a promising platform for quantum computing (4–7). Ideas from these fields have been successfully transposed to other architectures such as optomechanical systems (8). In these systems, phonons in mechanical modes can interact with photons of both microwave and optical domains, offering a promising platform for transducing quantum information between microwave-only quantum systems, such as superconducting qubits, and photons in optical fibers (8–10).

Recently, a novel approach enabling bidirectional conversion between microwave and optical photons using their mutual interaction with macroscopic collective spin excitation modes in ferromagnetic insulators has been explored (11–14). Combined with the coherent interaction between the magnons in these magnetostatic modes and superconducting qubits (15, 16), this demonstration opens up the possibility of transducing quantum information between a superconducting quantum processor and photons in optical fibers. However, a key ingredient for using quantum magnonics systems as quantum transducers is the capability of encoding arbitrary qubit states in magnon nonclassical states.

RESULTS

The coherent interaction between magnons and a superconducting qubit was previously demonstrated through the observation of a magnon-vacuum Rabi splitting of the qubit (15). Here, we go further and explore the off-resonant, dispersive regime of quantum magnonics, a promising regime to probe and control magnon states using the superconducting qubit. In circuit quantum electrodynamics, the strong dispersive interaction between a qubit and a microwave cavity has been used as a quantum sensor of the electromagnetic field of the cavity (17, 18) and to create and manipulate nonclassical states of microwave light (19, 20). Here, we demonstrate the ability to reach the strong dispersive regime in quantum magnonics by probing magnons at the level of single quanta in a millimeter-sized ferromagnet using spectroscopic measurements of the qubit. Our demonstration opens up the possibility of measuring, creating, and manipulating macroscopic nonclassical magnon states in ferromagnetic systems.

Our hybrid system consists of a superconducting qubit and a single-crystalline yttrium iron garnet (YIG) sphere inside a three-dimensional microwave cavity (Fig. 1A). The transmon-type superconducting qubit has a resonant frequency of 7.9905 GHz (21). A pair of permanent magnets and a coil are used to apply a magnetic field B₀ to the YIG sphere, making it a single-domain ferromagnet. The electric dipole of the qubit and the magnetic dipole of the ferromagnet couple to the electric and magnetic fields of the cavity modes, respectively. The YIG sphere is placed near the antinode of the magnetic field of the transverse electric TE₁₀₂ cavity mode, so that the cavity field is nearly uniform throughout the 0.5-mm sphere. This makes the uniformly precessing mode, or Kittel mode, the most dominantly coupled magnetostatic mode. As detailed in section S2, the interaction strength g_m-c between the TE₁₀₂ cavity mode, or coupler mode, and the Kittel mode reaches the strong coupling regime (22–26), where g_m-c/2π = 22.5 MHz is much larger than both the cavity (κ_c/2π = 2.08 MHz) and magnon (γ_m/2π = 1.3 MHz) linewidths.

Fig. 1. Hybrid system and qubit-magnon coherent interaction.

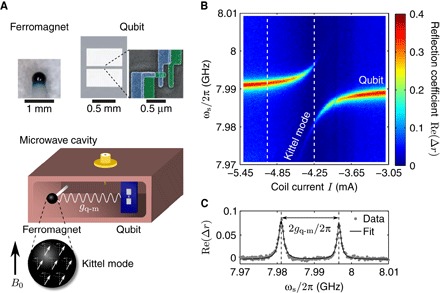
(A) Schematic illustration of a ferromagnetic YIG sphere and a superconducting transmon qubit inside a three-dimensional microwave cavity. A magnetic field B₀ is applied to the YIG sphere using permanent magnets and a coil. The magnetostatic mode in which spins uniformly precess in the ferromagnetic sphere, or the Kittel mode, couples to the magnetic field of the cavity modes. The qubit and the Kittel mode interact through virtual excitations in the cavity modes at a rate g_q-m. (B) The spectrum of the qubit is measured by probing the change of the reflection coefficient Re(Δr) of a microwave excitation resonant, with the probe mode at frequency ω_p as a function of the spectroscopy frequency ω_s and the coil current I, changing the magnetic field at the ferromagnet. The avoided crossing indicates a coherent interaction between the qubit and the Kittel mode. Vertical dashed lines indicate that I = −4.25 mA, where the qubit and the Kittel mode are hybridized (Fig. 1D), and that I = −5.02 mA, where the qubit-magnon interaction is in the dispersive regime (Figs. 2 to 4). (C) Magnon-vacuum Rabi splitting of the qubit on resonance, with the Kittel mode at I = −4.25 mA. From the fit, we extract the qubit-magnon coupling rate g_q-m/2π = 7.79 MHz.

The coupling of the superconducting qubit and the Kittel mode to the same cavity modes creates an effective interaction between these two macroscopic systems (15, 16). To verify that this interaction is coherent, we perform spectroscopic measurements of the qubit with the hybrid system in the quantum regime at a temperature of 10 mK. Although the qubit-magnon coupling is mostly provided by the TE₁₀₂ cavity mode at 8.4563 GHz (coupler mode), we use the dispersive interaction of the qubit with the TE₁₀₃ cavity mode at 10.4492 GHz (probe mode) to read out the qubit. This scheme avoids measurement-induced dephasing caused by photon number fluctuations in the coupler mode (16, 17). The change in the reflection coefficient r of a probe microwave tone, resonant with the probe mode and containing less than one photon on average, is measured while exciting the qubit with a spectroscopic microwave tone at frequency ω_s. Figure 1B shows the real part of the change of the reflection coefficient, Δr, measured for different currents I in the coil, changing the frequency ω_m ∝ B₀ of the magnons in the Kittel mode. The avoided crossing indicates the coherent interaction between the qubit and the Kittel mode (15). The qubit-magnon coupling strength g_q-m of 7.79 MHz, obtained from the magnon-vacuum Rabi splitting of the qubit (Fig. 1C), is much larger than both the power-broadened qubit linewidth γ_q/2π = 1.74 MHz and the magnon linewidth γ_m/2π= 1.3 MHz.

We now investigate the dispersive regime of our hybrid system, where the detuning between the bare qubit and Kittel mode frequencies, |ω_q^bare − ω_m^bare|, is much larger than g_q-m. The exchange of quanta of excitations between the qubit and the Kittel mode, through virtual photons in the coupler cavity mode, is then highly suppressed. The dispersive part of the qubit-magnon Hamiltonian is then given by

$${\widehat{\mathit{H}}}_{\mathrm{q}‐\mathrm{m}}^{\text{disp}}=\mathrm{\hslash }{\mathrm{\chi }}_{\mathrm{q}‐\mathrm{m}}{\widehat{\mathrm{\sigma }}}_{\mathit{z}}{\widehat{\mathit{c}}}^{†}\widehat{\mathit{c}}$$ (1)

where ${\widehat{\mathrm{\sigma }}}_{\mathit{z}}=|\mathit{e}\rangle \langle \mathit{e}|-|\mathit{g}\rangle \langle \mathit{g}|$, with |g(e)〉 the ground (excited) state of the transmon qubit, ${\widehat{\mathit{c}}}^{†}$ ($\widehat{\mathit{c}}$) is the magnon creation (annihilation) operator, and χ_q-m is the qubit-magnon dispersive shift (4, 16). This dispersive interaction makes the qubit and magnon frequencies dependent on the state of the other system. More precisely, the qubit frequency ω_q^(nm) depends on the magnon number state |n_m = {0, 1, 2, …}〉, and the magnon frequency ω_mⁱ depends on the transmon state |i = {g, e, f, …}〉. As illustrated in Fig. 2A, the strong dispersive regime, where |2χ_q-m| > max[γ_q,γ_m], enables the observation of magnon number states |n_m〉 via magnon number–dependent ac Stark shift of the qubit frequency (17, 18).

Fig. 2. Dispersive qubit-magnon interaction.

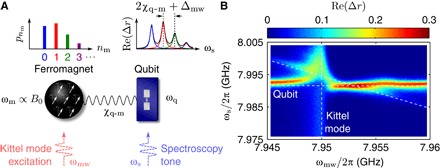
(A) Schematic illustration of the hybrid system in the strong dispersive regime. A microwave excitation at frequency ω_mw is used to create a magnon coherent state in the Kittel mode. The excitation is detuned from the magnon frequency, with the qubit in the ground state, ω_m^g, by Δ_mw = ω_m^g − ω_mw. In the strong dispersive regime, magnon number states |n_m〉 (of probability distribution ${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}$) are mapped into the qubit spectrum as peaks at frequencies ${\tilde{\mathrm{\omega }}}_{\mathrm{q}}^{({\mathit{n}}_{\mathrm{m}})}={\mathrm{\omega }}_{\mathrm{q}}^{({\mathit{n}}_{\mathrm{m}})}+{\mathit{n}}_{\mathrm{m}}{\mathrm{\Delta }}_{\text{mw}}$, separated by 2χ_q-m + Δ_mw and with a spectral weight closely related to ${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}$. (B) Measurement of the qubit spectrum for a coil current I = −5.02 mA as a function of the Kittel mode excitation frequency ω_mw and the spectroscopy frequency ω_s. The excitation frequency producing the maximum magnon-induced ac Stark shift of the qubit from ω_q (horizontal dashed line) yields an estimation of ω_m^g/2π ≈ 7.95 GHz (vertical dashed line). The Kittel mode spectrum, measured via its dispersive interaction with the probe mode, appears as a faint vertical line at ~7.95 GHz. The signature corresponding to the two-photon transition involving both the spectroscopy and the excitation photons and exciting both the qubit and a magnon (fig. S1) is indicated by the diagonal dashed line given by ${\mathrm{\omega }}_{\mathrm{s}}={\mathrm{\omega }}_{\mathrm{q}}^{({\mathit{n}}_{\mathrm{m}}=0)}+2{\mathrm{\chi }}_{\mathrm{q}‐\mathrm{m}}+{\mathrm{\Delta }}_{\text{mw}}$, calculated with χ_q-m/2π = 1.5 MHz at ω_m^g/2π = 7.95 GHz.

The qubit-magnon dispersive regime is investigated through spectroscopic measurements of the qubit while exciting the Kittel mode at frequency ω_mw, detuned by Δ_mw = ω_m^g − ω_mw from the dressed magnon frequency ω_m^g. The measurement of the qubit spectrum while sweeping ω_mw for a coil current of −5.02 mA and a Kittel mode excitation power P_mw of 7.9 fW is shown in Fig. 2B. Near resonant excitation Δ_mw ~ 0, the qubit is ac Stark–shifted by the magnon occupancy in the Kittel mode, a signature of the qubit-magnon dispersive interaction similar to the qubit-photon counterpart in circuit quantum electrodynamics experiments (17, 27). The positive magnon-induced ac Stark shift shows that χ_q-m > 0, and the excitation frequency producing the maximum shift indicates that ω_m^g/2π ≈ 7.95 GHz. Both these features are consistent with the hybrid system being in the straddling regime (fig. S1) (21, 28). Notably, the signature corresponding to the two-photon transition, from |g, n_m = 0〉 to |e, n_m = 1〉, involving both the spectroscopy and the excitation photons and exciting both the qubit and a magnon (fig. S1), is also visible at ${\mathrm{\omega }}_{\mathrm{s}}={\mathrm{\omega }}_{\mathrm{q}}^{({\mathit{n}}_{\mathrm{m}}=0)}+2{\mathrm{\chi }}_{\mathrm{q}‐\mathrm{m}}+{\mathrm{\Delta }}_{\text{mw}}$.

We now focus on resolving the magnon number states through measurements with the excitation frequency close to resonance with the Kittel mode (Δ_mw≪γ_m). In the qubit spectra shown in Fig. 3, the excitation frequency is fixed at 7.95 GHz, close to resonance with ω_m^g for I = −5.02 mA (Fig. 2B). The microwave excitation creates a magnon coherent state in the Kittel mode. When coherently driving the Kittel mode, we observe peaks in the qubit spectrum at frequencies higher than the zero-magnon peak. As shown next, these peaks correspond to different numbers of magnons in the Kittel mode.

Fig. 3. Resolving magnon number states.

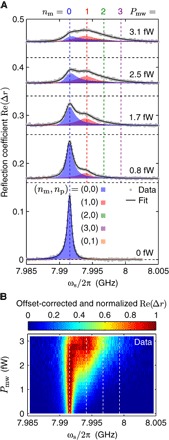
(A) Measurements of the qubit spectrum at different Kittel mode excitation powers P_mw for a coil current of −5.02 mA and Kittel mode excitation frequency of 7.95 GHz. Black lines show fits of the data to the spectrum of a qubit dispersively coupled to a harmonic oscillator. Color-coded shaded areas show components of the spectrum corresponding to different photon number states |n_p〉 of the probe cavity mode and magnon number states |n_m〉. Vertical offsets are shown by horizontal dashed lines. (B) Measured qubit spectra as a function of P_mw. For clarity, after subtracting a power-dependent offset, Re(Δr) is normalized relative to its maximum for each drive power. For both (A) and (B), vertical dashed lines indicate the frequencies of the qubit |g〉 ↔ |e〉 transitions corresponding to the first four magnon number states, neglecting a power-dependent ac Stark shift, which is small relative to the dispersive shift per magnon for this range of P_mw.

To fit the data of Fig. 3, we used an analytical model of the spectrum of a qubit dispersively coupled to a harmonic oscillator (17). The asymmetric qubit line shape at P_mw = 0 is well reproduced by including in the fit the photonic contribution to the qubit line shape from the dispersive interaction between the qubit and the probe mode (section S4). The fitting parameters for each excitation power are the occupancy of the Kittel mode ${\overline{\mathit{n}}}_{\mathrm{m}}^{\mathit{g}}=\langle {\widehat{\mathit{n}}}_{\mathrm{m}}{\widehat{\mathrm{\prod }}}_{\mathrm{q}}^{\mathit{g}}\rangle$ (where ${\widehat{\mathrm{\prod }}}_{\mathrm{q}}^{\mathit{g}}=|\mathit{g}\rangle \langle \mathit{g}|$ is the projector to the qubit ground state), the qubit-magnon dispersive shift (χ_q-m), and the excitation detuning (Δ_mw) (Fig. 3A). More information on the theory and the fitting procedure can be found in sections S3 to S5. We find a detuning Δ_mw of −0.38 MHz, indicating a bare magnon frequency ω_m^bare of 7.9515 GHz. The condition for the dispersive regime is therefore respected with a detuning |ω_q^bare − ω_m^bare| of 89 MHz, much larger than the qubit-magnon coupling strength. The qubit-magnon dispersive shift χ_q-m is found to be 1.5 ± 0.1 MHz, in good agreement with the theoretical value of 1.27 MHz (fig. S1). Resolving magnon number states demonstrates that we have reached the strong dispersive regime of quantum magnonics, with the dispersive shift per magnon 2χ_q-m being larger than both the power-broadened qubit linewidth γ_q/2π = 0.78 MHz and the magnon linewidth γ_m/2π = 1.3 MHz.

The average number of magnons ${\overline{\mathit{n}}}_{\mathrm{m}}^{\mathit{g}}$ in the Kittel mode extracted from the fit of the data is shown in Fig. 4A. At the lowest excitation power of 79 aW, we are able to resolve 0.026 ± 0.012 magnons in the Kittel mode of the ferromagnetic sphere containing about 1.4 × 10¹⁸ spins. We are therefore able to resolve a change in the magnetic moment of the ferromagnet equivalent to a single spin flipped among ~5 × 10¹⁹ spins. Within our resolution of about 0.01 magnons, no thermal occupancy of the Kittel mode is observed, indicating that the millimeter-sized ferromagnet is indeed in its magnon-vacuum state. Furthermore, the nonlinearity of ${\overline{\mathit{n}}}_{\mathrm{m}}^{\mathit{g}}$ against the excitation power can be explained by a Kerr nonlinearity in the Kittel mode caused by the anharmonicity of the transmon (3, 29). We find a Kerr coefficient of −0.20${\pm }_{0.13}^{0.09}$ MHz in good agreement with the expected value of −0.12 MHz (fig. S1).

Fig. 4. Magnon occupancy and probability distribution.

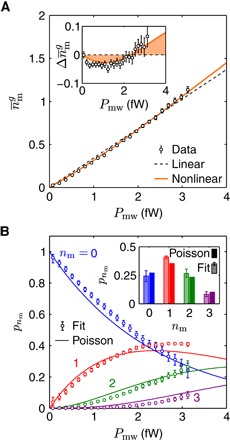
(A) Magnon occupancy ${\overline{\mathit{n}}}_{\mathrm{m}}^{\mathit{g}}$ as a function of the excitation power P_mw. Dashed black line and solid orange line show fits to a driven linear and nonlinear Kittel mode, respectively. Inset: Deviations $\mathrm{\Delta }{\overline{\mathit{n}}}_{\mathrm{m}}^{\mathit{g}}$ from the linear fit, indicating a significant magnon Kerr nonlinearity. (B) Probability ${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}$ of the first four magnon number states as a function of P_mw. Poisson distributions are shown as solid lines. Inset: ${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}$ for P_mw = 3.1 fW. For both (A) and (B), error bars correspond to 95% confidence intervals.

Finally, we estimate the probability ${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}$ of having n_m magnons in the Kittel mode with

$${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}\approx {\displaystyle \int }\mathit{d}{\mathrm{\omega }}_{\mathit{s}}{\mathit{S}}_{{\mathit{n}}_{\mathrm{m}}}({\mathrm{\omega }}_{\mathit{s}})/\mathit{S}({\mathrm{\omega }}_{\mathit{s}})$$ (2)

where $\mathit{S}({\mathrm{\omega }}_{\mathrm{s}})\approx {\displaystyle {\sum }_{{\mathit{n}}_{\mathrm{m}}=0}^{10}}{\mathit{S}}_{{\mathit{n}}_{\mathrm{m}}}({\mathrm{\omega }}_{\mathrm{s}})$ is the qubit spectrum in the analytical model, to which data are fitted, and ${\mathit{S}}_{{\mathit{n}}_{\mathrm{m}}}({\mathrm{\omega }}_{\mathrm{s}})$ is its component associated with the magnon number state |n_m〉. For 2χ_q-m≫γ_m, the probability distribution calculated with Eq. 2 falls back to the Poisson distribution expected for a driven harmonic oscillator (section S5) (17). The probability distributions ${\mathit{p}}_{{\mathit{n}}_{\mathrm{m}}}$ of the first four magnon number states, shown in Fig. 4B, indicate small deviations from Poisson distributions. This is expected because the qubit-magnon dispersive shift is only slightly larger than the magnon linewidth in our hybrid system (section S5). Nevertheless, our ability to map the probability distribution of magnon number states to the spectrum of a qubit provides a novel tool for investigating quantum states in magnetostatic modes.

DISCUSSION

Looking forward, the strong dispersive interaction between magnons and a superconducting qubit demonstrated here should enable the encoding of the qubit into a superposition of magnon coherent states in a magnetostatic mode (19, 20). However, to implement this encoding protocol, the qubit-magnon system needs to be deeper into the strong dispersive regime, either by increasing the qubit-magnon coupling strength or by decreasing the magnon linewidth in the quantum regime (23). Together with the recently demonstrated bidirectional conversion between microwave and optical photons in YIG (12), this could pave the way to the transfer of quantum states between superconducting qubits and photons in optical fibers. Combining two very promising candidates for both stationary and flying qubits, such a breakthrough would be an important step toward the realization of a superconducting qubit–based quantum network. Furthermore, the ability to count the number of magnons in a millimeter-sized ferromagnetic insulator in the quantum regime from zero up to a few magnons could be used to study microscopic mechanisms of collective spin excitations, such as decay, scattering, and coupling to a bath of two-level systems. Finally, the demonstrated architecture of quantum magnonics could also be used in applications in spintronics and spin-based quantum information processing (30).

MATERIALS AND METHODS

Figure S2 shows the instruments and components used in the experiment. Microwave powers P_r, P_s, and P_mw were calibrated using the input of the cavity as the reference point. At that reference point, the reflection coefficient r is in unity when |ω_r − ω_10p|≫κ_10p, where ω_r is the readout frequency and ω_10p and κ_10p are the resonant frequency and the linewidth of the TE_10p cavity mode, respectively, with p = 1,2,3…. By taking into account the attenuation in cables outside and inside the dilution refrigerator, the total attenuations between the microwave sources and the input of the cavity are approximately 81, 122, and 121 dB for the readout, spectroscopy, and Kittel mode microwave excitations, respectively.

The yoke, coil, cavity, and YIG sphere of the hybrid system used in the paper were the same as in the study by Tabuchi et al. (15), whereas the transmon qubit was a different one. The oxygen-free copper microwave cavity had dimensions of 24 × 3 × 53 mm³. An SMA (subminiature version A) connector connected to the cavity was used to measure the reflection coefficient r. A pair of disc-shaped neodymium permanent magnets, with a diameter of 10 mm and a thickness of 1 mm each, were placed at the ends of a magnetic yoke made of pure iron. The magnets produced a static field B₀ ≈ 0.29 T in the 4-mm gap between them. The magnetic field can be additionally tuned by a current I in a 10⁴-turn superconducting coil. The field-to-current conversion ratio is approximately 1.7 mT/mA. A YIG sphere glued to an aluminum oxide rod along the 〈110〉 crystal axis was mounted in the cavity at the center of the gap between the magnets. The static field was applied in parallel with the 〈100〉 crystal axis. A transmon-type superconducting qubit, consisting of two large-area aluminum pads and a single Josephson junction (Al/Al₂O₃/Al), was fabricated on a silicon substrate and was mounted inside the cavity. The qubit and the YIG sphere were separated by 35 mm in the horizontal direction. A double-layer magnetic shield made of aluminum and pure iron covered half of the cavity to protect the qubit from the stray magnetic field of the magnet.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1603150/DC1

section S1. Hamiltonian of the hybrid system

section S2. Cavity-magnon coupling

section S3. Qubit spectrum in the dispersive regime

section S4. Qubit spectroscopy—Magnon vacuum state

section S5. Qubit spectroscopy—Magnon coherent state

section S6. Magnon Kerr nonlinearity

fig. S1. Qubit-magnon hybrid system.

fig. S2. Experimental setup.

fig. S3. Cavity-magnon coupling.

fig. S4. Power broadening of the qubit spectrum.

fig. S5. Dispersive qubit-magnon interaction.

fig. S6. Probability distributions.

fig. S7. Magnon Kerr nonlinearity.

fig. S8. Effect of the finite Kerr nonlinearity on the magnon probability distribution.

table S1. Parameters of the hybrid system.

table S2. Comparison between experimental and theoretical values.

table S3. Linewidths of the hybrid system.

table S4. Experimental parameters of the measurements.

References (31–34)