The Remarkable Amphoteric Nature of Defective UiO‐66 in Catalytic Reactions

Abstract

One of the major requirements in solid acid and base catalyzed reactions is that the reactants, intermediates or activated complexes cooperate with several functions of catalyst support. In this work the remarkable bifunctional behavior of the defective UiO‐66(Zr) metal organic framework is shown for acid‐base pair catalysis. The active site relies on the presence of coordinatively unsaturated zirconium sites, which may be tuned by removing framework linkers and by removal of water from the inorganic bricks using a dehydration treatment. To elucidate the amphoteric nature of defective UiO‐66, the Oppenauer oxidation of primary alcohols has been theoretically investigated using density functional theory (DFT) and the periodic approach. The presence of acid and basic centers within molecular distances is shown to be crucial for determining the catalytic activity of the material. Hydrated and dehydrated bricks have a distinct influence on the acidity and basicity of the active sites. In any case both functions need to cooperate in a concerted way to enable the chemical transformation. Experimental results on UiO‐66 materials of different defectivity support the theoretical observations made in this work.

Introduction

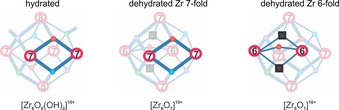
Over the past years, zirconium‐based metal‐organic frameworks (Zr‐MOFs) have received considerable attention because they exhibit exceptional thermal, mechanical and chemical properties compared to other common MOFs.1 Several zirconium‐based materials such as UiO‐66, NU‐1000 and MOF‐808 were extensively explored for various catalytic transformations.1b, 2 Within this series the UiO‐66 framework received the most attention. The porous crystalline network of UiO‐66 consists of Zr₆O₄(OH)₄ octahedral inorganic bricks connected by twelve 1,4‐benzenedicarboxylate (BDC) linkers.1a The remarkable thermal stability of this material is attributed to the high degree of coordination with organic linkers and to the structural composition of UiO‐66 which has the face‐centered symmetry of the Fm $\bar{3}$ m space group. To activate the material for catalysis, coordinatively unsaturated metal sites need to be generated. A plethora of experimental studies gave substantial evidence for a high concentration of structurally embedded defects in the as‐synthesized UiO‐66 material. Thus in general the framework connectivity is less than 12.3 The synthesis procedures have been meticulously tuned to control to a large extent the concentration of defects in the final material. Defect engineering of framework materials is one method to structurally embed coordinatively unsaturated sites in the material.3e, 4 In addition it has been reported that upon thermal treatment the inorganic hexanuclear Zr core Zr₆O₄(OH)₄ is dehydrated and rearranged into a distorted Zr₆O₆ node.3a–3c, 5 Upon water removal from the inorganic brick the Zr₆O₆ node has a D _3d(‐3m) point symmetry, showing a preferential squeezing direction.3c These dehydration procedures also lead to a reduction of the coordination of the zirconium sites (Figure 1).

Figure 1.

Periodic model of UiO‐66 with indicated unit cell and encircled two types of bricks. Zr‐brick 1 with formula [Zr₆O₄(OH)₄]¹²⁺ is intact without missing linker, whereas brick 2 [Zr₆O₆(OH)₂]¹⁰⁺ has in total two terephthalate linkers missing, one at site A and one at the opposite site B. On the right, the dehydration processes of brick 1 and brick 2 are shown. Coordination number of different Zr atoms in the brick are encircled in red. Oxygen vacancies are displayed as grey squares.

These two types of framework distortion, linker and metal vacancies, create point defects, decreasing the coordination number of Zr and creating Lewis acid sites, which make UiO‐66 an outstanding candidate for application in catalysis4d, 6 (Figure 1).

The UiO‐66 material has mainly been studied for Lewis acid catalyzed reactions such as the citronellal cyclization,6d, 7 or esterification.8 A series of computational and experimental studies was conducted to unravel the nature of the active sites. Indeed, owing to the large number of possibilities to remove linkers in combination with the dehydration mechanisms, a large amount of structures may theoretically be proposed.9 The effect of linker removal on the catalytic performance and stability of the material has been studied recently. Furthermore, computational attempts have been made to describe the process of dehydration.5 It has been found that the dehydration of the structure with one linker defect results in the creation of Zr Lewis acid sites which are 6‐fold coordinated. To the best of our knowledge, the comparison of the catalytic behavior of the hydrated and dehydrated UiO‐66 has never been made.

However, the dehydration mechanism may have a decisive effect on certain catalytic reactions, in which next to the Lewis acid site also the neighboring Brønsted base or acid site may take a cooperative role in the reaction mechanism. This was recently shown for the condensation reaction to form the jasminaldehyde condensation product from benzaldehyde and heptanal.6b In this case the cooperation of both the Lewis acid site and Brønsted base site is essential in the formation of the active site. A profound understanding of the strength of Brønsted and Lewis sites within MOFs is very important to tune the catalytic activity for a broad variety of acid, base or acid‐base catalyzed reactions.

To the best of our knowledge, the nature of active sites upon calcination and catalytic activity of hydrated and dehydrated UiO‐66 have not been studied computationally so far. In the current work, we will make use of the Oppenauer oxidation reaction, which is schematically shown in Figure 2, to rationalize the catalytic effect of the structurally incorporated defects including linker removal and hydration/dehydration of the framework. Furthermore, our theoretical findings are supported by new experimental data conducted on various defective UiO‐66 materials in hydrated and dehydrated conditions.

Figure 2.

Oppenauer oxidation of primary alcohol prenol with furfural.

Dehydrogenation of alcohols requires acid‐base site pairs of intermediate strength;10 and in this respect the Oppenauer oxidation of alcohols to carbonyl compounds on UiO‐66 is an ideal case to study the influence of both missing linkers and dehydration of the structure on the catalytic activity. The reaction mechanism of the reverse Meerwein‐Ponndorf‐Verley (MPV) reduction of aldehydes and ketones has been studied both theoretically and experimentally on Zr‐beta zeolites by Boronat et al.11 The similarity between the active sites in the Zr‐beta zeolites and the UiO‐66 framework is particularly interesting. A schematic representation of potential active sites in both materials is shown in Figure 3.

Figure 3.

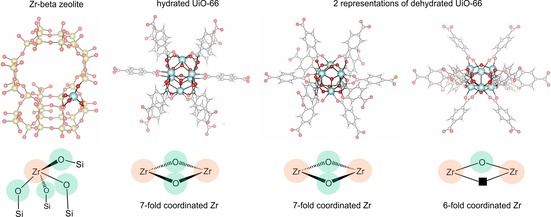
Representation of Zr‐beta zeolite, hydrated UiO‐66 and dehydrated UiO‐66 with indicated active sites. In each configuration zirconium Lewis acid sites are encircled in orange and oxygen Brønsted base sites in green. On the dehydrated, 6‐fold coordinated Zr brick the oxygen vacancy is indicated by a black square.

Zr‐beta zeolite is a Zr‐substituted zeolite containing welldefined and isolated Lewis acid centers (‐Si‐O‐)₄Zr which were shown to be bifunctional in the MPV reduction of carbonyl compounds. Boronat et al.11 demonstrated that the aldehyde (cyclohexanone) and the alcohol (2‐butanol) are coordinated to the same single Zr‐center, acting as a Lewis acid site, and that the adjacent basic oxygen atom assists in deprotonating the alcohol. The hydride shift can then take place converting simultaneously cyclohexanone into cyclohexanol and 2‐butanol into 2‐butanone. Clearly, the inorganic octahedral Zr‐bricks in UiO‐66 with bridging μ₃‐oxygens and OH‐groups show large similarities with the partially hydrolyzed framework Zr‐OH group in Zr‐beta zeolite. Although the reaction mechanism of the MPV reduction and the heterolytic hydrogen transfer in Zr‐beta zeolite seems to be quite clear, it remains to be investigated what the respective role is of the acid and basic sites in the UiO‐66 catalyst, and how catalytic activity is influenced by modification of the UiO‐66 framework and its multiple defect structures. Therefore, the Oppenauer oxidation of alcohols is an ideal choice to evaluate the nature of active sites encountered in the different modified frames. De Vos and co‐workers6d were the first to test this oxidation reaction in UiO‐66. In the oxidation of geraniol by furfural over UiO‐66 they noticed a geraniol conversion of 20 % which could be even drastically increased by functionalizing the linkers with electron‐withdrawing substituents such as NO₂, reaching conversion coefficients of 70 % under the same catalytic conditions. Furthermore, thermogravimetric analysis profiles revealed that of the 12 linkers surrounding each Zr‐brick, approximately three were on average missing.

The MPV reduction has also been investigated on various types of metal oxides showing that the hydrogen transfer can proceed on Lewis acid catalysts or on catalysts having basic properties.12

Results and Discussion

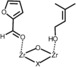
In this theoretical study we took prenol as an alcohol which is a smaller version of the much larger geraniol molecule. Prenol or 3‐methyl‐2‐buten‐1‐ol is a building block of isoprenoid alcohols of which geraniol is the smallest. To evaluate the direct reduction of furfural by this alcohol, calculations were performed on a periodic model taking into account the full topology of the material, allowing an accurate quantification of the confinement effects induced by the environment of the nanoporous material. A periodic UiO‐66 structure was selected following a procedure as was described in a previous work of some of the present authors.6b A tetragonal unit cell containing two inorganic Zr‐bricks was taken out from the conventional cubic cell of UiO‐66 (Figure 1). The selected structure had one linker missing on average with unit cell formula [Zr₆O₄(OH)₄]¹²⁺[Zr₆O₆(OH)₂]¹⁰⁺. Each brick is characterized by its coordination number and in this case one brick (Brick 1) is fully coordinated by 12 organic linkers, whereas the other brick (Brick 2) is 10‐fold coordinated and is active for catalysis. Brick 2 has a structure which contains four 7‐fold and two 8‐fold coordinated Zr sites (Figure 1). Upon the dehydration process the coordination numbers of the Zr‐atoms in the brick change: four 7‐fold coordinated and two 6‐fold coordinated Zr atoms and oxygen vacancies appear. In the case of two 6‐fold coordinated Zr atoms the oxygen atom is located centrally between them (Figure 1, Figure 4, right).

Figure 4.

Representation of active sites for catalysis in brick 2 on the hydrated and dehydrated UiO‐66. Oxygens are represented by medium circles. Their color can differ but has no real physical significance and originates from ref.5b.

The true interest lies in the nature of these different coordinated Zr sites and their influence in a catalytic process. It has been theoretically found that the activity of UiO‐66 for jasminaldehyde condensation is related to the presence of Zr‐O‐Zr motifs. These sites are bifunctional and consist of the Lewis acidic zirconium atom that activates the carbonyl group and the adjacent basic μ₃‐oxygen atom which attracts a proton.6b In the UiO‐66 material with one linker defect (in the unit cell of two inorganic bricks) we thus distinguish between three active Zr‐sites as displayed in Figure 4. The influence of these structural defects on the Oppenauer reaction will be investigated.

A very particular characteristic of the Oppenauer‐type reaction is that an alcohol is oxidized to the corresponding carbonyl compound. Furfural is a strong oxidant and was chosen as a perfect probe Lewis base molecule to track the Lewis acid strength of the Zr centers of the active site, which are 7‐ and 6‐fold coordinated. The physisorption of the aldehyde to the metal atom polarizes and activates the carbonyl double bond. The strong interaction between the carbonyl functional group and the Lewis acid site induces a transfer of a significant part of the electron density to the Zr site. The adsorption of furfural corresponds to the first step of the reaction scheme shown in Figure 5. Rather surprisingly, the adsorption of furfural on a hydrated or dehydrated site does not cause large differences in adsorption strength. The adsorption energy on the two active Zr sites (Zr(7)‐O‐Zr(7) and Zr(6)‐O‐Zr(6)) is about 5.0 kJ mol⁻¹ stronger than on the hydrated material (Table 1, Figure 5, configuration 1) This results shows that the Lewis acidity is not significantly altered between hydrated and dehydrated bricks.

Figure 5.

Free energy profile of the Oppenauer oxidation of prenol with furfural (periodic with PBE‐D3) given at 393.15 K. Hydrated brick is indicated by a blue line, whereas dehydrated 7‐ and 6‐fold coordinated Zr by a red and green line, respectively. X corresponds to: X=O in the hydrated and dehydrated 7‐fold material, and X=vacancy for the cluster with 6‐fold Zr coordination. R corresponds to the reactants in gas phase and the catalyst, P corresponds to the final products in gas phase and the catalyst.

Table 1.

Enthalpy, entropy and free energy contributions given in kJ mol⁻¹ for the Oppenauer oxidation, given at 393.15 K.

state	Hydrated, Zr 7‐fold			Dehydrated, Zr 7‐fold			Dehydrated, Zr 6‐fold
	ΔH	−TΔS	ΔG	ΔH	−TΔS	ΔG	ΔH	−TΔS	ΔG
1	−87.8	66.3	−21.5	−91.8	65.9	−25.9	−87.9	63.5	−24.4
2	−174.5	143.6	−30.9	−173.3	140.5	−32.9	−161.8	135.1	−26.7
Ts1	−166.9	143.4	−23.5	−143.7	147.5	3.8	−117.0	141.2	24.2
3	−207.3	139.7	−67.6	−180.5	136.2	−44.3	−124.1	135.4	11.3
Ts2	−141.2	153.1	11.9	−138.5	149.0	10.5	−84.6	154.3	69.8
4	−213.5	134.5	−79.0	−200.2	142.6	−57.6	−148.0	139.7	−8.2
Ts3	−140.2	141.7	1.5	−136.9	144.8	7.9	−130.2	148.5	18.3
5	−170.6	137.5	−33.1	−189.1	140.3	−48.7	−193.6	140.6	−53.0
P	−24.2	−0.8	−25.1	−24.3	−0.8	−25.1	−24.3	−0.8	−25.1

The next step of the reaction consists of co‐adsorption of the alcohol at the adjacent zirconium atom. The adsorption strength is almost equally strong on the three considered active sites. Configuration 2 shows an adsorption free energy of about 30 kJ mol⁻¹ for the three types of UiO‐66 material. Overall the second reactant has a weak free energy of co‐adsorption. The enthalpic co‐adsorption energy is relatively large but is to a large extent compensated by a positive entropic contribution, originating from the loss of degrees of freedom associated with the adsorption. One would expect a stronger local Lewis acid strength for the under‐coordinated Zr(6) center but previous observations learn that the Lewis acid character of the active site is not concentrated in discrete Zr‐atoms, but rather distributed over the Zr‐centers and their bond with the adjacent μ₃‐oxygens. The specific coordination number of Zr has a minor effect on the Lewis acid strength of the active site.

The observed behavior here can be related to some characteristic Zr−O bond lengths in the various adsorption complexes. The critical distances are taken up in Table 2. We distinguish three types of Zr−O bonds: Zr−O in the inorganic brick, Zr‐O between the metal and the carbonylic oxygen of the aldehyde and Zr‐O between the metal and the oxygen of the alcohol. In the adsorbed complexes 1 and 2 the distances between the adsorbates and the active Zr‐site vary only slightly between the hydrated and the two dehydrated materials. On the other hand, the optimized Zr−O bond length in the brick is 0.2 Å shorter in the site composed of the 6‐fold coordinated Zr‐centers than in the 7‐fold coordinated materials. The shorter the bond length the stronger the covalent Zr−O interactions. The shorter Zr−O length in the Zr(6)‐O‐Zr(6) site can partially be assisted by the presence of a vacancy instead of a bridging oxygen (Figure 4).

Table 2.

Evolution of the various Zr−O distances during the Oppenauer reaction on the three UiO‐66 materials. X corresponds to: X=O in the hydrated and dehydrated 7‐fold material, and X=vacancy in the 6‐fold coordinated site.

structure	1	2	Ts1	3	Ts2	4
	[Å]	[Å]	[Å]	[Å]	[Å]	[Å]
Hydrated
Zr‐O inorganic brick	2.142	2.167	2.230	2.291	2.302	2.271
Zr‐O aldehyde	2.412	2.417	2.371	2.335	2.227	2.025
Zr‐O alcohol	–	2.396	2.243	2.017	2.132	2.276
Dehydrated Zr 7‐fold
Zr‐O inorganic brick	2.097	2.120	2.189	2.275	2.302	2.298
Zr‐O aldehyde	2.384	2.403	2.354	2.348	2.177	2.011
Zr‐O alcohol	–	2.457	2.239	1.999	2.146	2.350
Dehydrated Zr 6‐fold
Zr‐O inorganic brick	1.970	1.967	2.016	2.125	2.190	2.171
Zr‐O aldehyde	2.414	2.462	2.427	2.479	2.202	2.048
Zr‐O alcohol	–	2.476	2.201	1.984	2.194	2.412

Once the two reactants are adsorbed in state 2, the reaction further proceeds with the deprotonation of the alcohol to form the alkoxide (Figure 5, Ts1). The proton is transferred to the μ₃‐oxygen, which acts as a Brønsted base site. From this point on, the reactivity is substantially different in the three active sites (Figure 4). The reaction barrier for the deprotonation on the hydrated material is very low and amounts to only 7.4 kJ mol⁻¹, it raises to 36.7 kJ mol⁻¹ and 50.9 kJ mol⁻¹ on the dehydrated Zr(7)‐O‐Zr(7) and Zr(6)‐O‐Zr(6) material, respectively. The differences become even more pronounced in configuration 3 after the deprotonation has taken place and an alkoxide is formed. The alkoxide is much more stable on the hydrated brick compared to the dehydrated bricks. The lower the coordination numbers of the involved zirconium atoms the less stable the alkoxide becomes. In this case the electrons are more localized between the zirconium and oxygen atoms and therefore they are less available to attractively interact with a proton. On inspection of the enthalpic and entropic contributions to the free energy, it becomes clear that the large differences originate from electronic differences among the various active sites. The entropic contributions to the overall free energy are almost equally large (Table 1). The stabilization energy and enthalpy differs by more than 80 kJ mol⁻¹ between the hydrated and dehydrated 6‐fold configuration (Table S.1 ESI).

A plausible explanation may lie in the different base strengths of the μ₃‐oxygen bridging the two active Zr‐atoms. The Zr(6)‐O‐Zr(6) site has a substantially shorter Zr‐O distance, the Zr‐centers are only bridged by one single oxygen atom, and the brick is more compressed. The basicity of the bridging μ₃‐oxygen is weaker than in the hydrated brick (distances are tabulated in Table 2). The shorter the Zr−O bond, the more electronic density is concentrated in the zirconium‐oxygen bond and the electron density is less localized on the oxygen. Consequently, the oxygen is less basic. The energy barrier for the deprotonation reaction (Ts1) increases if the amount of μ₃‐hydroxy groups and coordination number of Zr decreases. The role of the active Zr‐O‐Zr surface in this deprotonation reaction may typically be attributed to that of an acid‐base bifunctional catalyst. The presence of the aldehyde in the adsorbed complex is crucial to keep the barrier for deprotonation low (mainly for the hydrated material). It enhances the basic character of the adjacent μ₃‐oxygen needed to form a strongly stabilized alkoxide complex at least on the two Zr(7)‐O‐Zr(7) surfaces.

With the formation of an alkoxide and the formation of a hydroxy group in the Zr‐OH‐Zr site of state 3, the zirconium oxygen distance increases in the three materials but remains the shortest in the dehydrated 6‐fold Zr‐site. Without the proton a value of 2.0 Å is found; it increases with 0.155 Å with the proton bound to the μ₃‐oxygen. The μ₃‐OH group may now take the role as a Brønsted acid site and will exert an influence in the further reaction. The intermediate structure 4 is the most stable adsorption complex for all three active sites.

To understand the underlying mechanism of the drastically stronger stabilization of the intermediate states 3 and 4 in the hydrated material, we removed the two adsorbates and replace them by one water molecule, constructing active sites as shown in Figure 6. The similarity with configuration 3 is large, the oxo‐atom is also protonated and one zirconium atom is covered with a hydroxy group. Essential is the presence of a μ₃‐OH in the brick. This model eliminates any influence arising from the choice of the adsorbates on the stabilization energies of the inorganic Zr‐bricks. Coordination of a water molecule on a hydrated Zr‐brick such as B′O(10¹²) in ref. 5b has been investigated theoretically in several works, but its influence on a dehydrated brick has not been studied before. The chemisorption energy and free energies of a water molecule on the three active sites are shown in Figure 6. Major differences for the three sites are observed with chemisorption energies varying from −95 kJ mol⁻¹ on the hydrated brick to −22 kJ mol⁻¹ on the 6‐fold coordinated dehydrated brick. The results are fully in line with the relative energies observed in configurations 3 and 4. The stabilization generated by a chemisorbed water molecule on a free active Zr‐O‐Zr surface in a hydrated brick is 72 kJ mol⁻¹ stronger than in a dehydrated 6‐fold Zr‐brick. Once the μ₃‐oxygen is protonated forming a hydroxy group bridging Zr‐centers, the physical and chemical properties of the whole brick change drastically. The hydrated brick with chemisorbed water is the most stable, as this brick resembles the most defective free brick in the pristine material. The 6‐fold dehydrated brick still shows quite large differences with the brick in the pristine material given the presence of oxygen vacancies in the close vicinity of the site.

Figure 6.

Influence of water coordination on the three active sites (hydrated Zr(7)‐O‐Zr(7), dehydrated 7‐fold Zr(7)‐O‐Zr(7) and dehydrated Zr(6)‐O‐Zr(6) UiO‐66).

In the next step the hydride shift between two reacting molecules can occur (Figure 5, Ts2). In this step the atoms from the catalyst are not actively involved into the mechanism of the six‐membered cyclic transition state and this is also shown by similar energy barriers for the hydride shift on the hydrated and dehydrated UiO‐66. The carbon–to–carbon hydride shift results in the formation of prenal, the first product of the Oppenauer oxidation (configuration 4).

In the last step of this reaction the proton is transferred from the catalyst to the reacting molecule (Figure 5, Ts3). Here the μ₃‐OH hydroxy group in the brick acts as a conjugate Brønsted acid site. Now, we get the opposite effect as observed in the deprotonation reaction (2→3). The acid proton is more loosely bound to the μ₃‐oxygen in the dehydrated 6‐fold material and jumps more easily to the negatively charged oxygen of the coordinated alkoxide to form furfuryl alcohol.

The proton transfer occurs much faster from the dehydrated UiO‐66 (free energy barrier of 26.5 kJ mol⁻¹) than from the hydrated material, which confirms that this μ₃‐oxygen atom retains the lowest basicity. Upon dehydration the basic properties were selectively lost though the Lewis acidic properties were conserved. ZrO₂ is a precursor of UiO‐66 and the bifunctional character of the inorganic node of UiO‐66 does not surprise if we consider the bulk properties of solid oxides. One of the most important and extensively studied properties of metal‐oxides is their acid‐base property. In this sense, ZrO₂ owing to its amphoteric character and its thermal stability has been investigated as a promising material for catalysis. Hydrated ZrO₂ calcined at 573–603 K was found to be highly active for complementary reduction of various carbonyl compounds with alcohol.13 It has also been found that the hydrous form of zirconium oxide is more efficient for MPV reduction than the anhydrous form.14 The reaction mechanism proposed here shows large similarities with the mechanism on the zirconium‐beta zeolite studied by Boronat et al.11 except for the fact that within the UiO‐66 material the reaction takes place at two zirconium sites. We investigated also similar reaction mechanism taking place on one zirconium site but these were all much higher activated.

The influence of both linker vacancies and the hydration state of the UiO‐66 framework on its potential to act as a catalyst in the Oppenauer oxidation of prenol with furfural was further probed experimentally. To this end, two UiO‐66 materials containing a different amount of linker vacancies were synthesized according to the procedure outlined by Shearer et al.,3a in which defect density can be steered by varying the molar ratio of terephthalic acid to ZrCl₄. In our case, molar ratios of 1/1 and 2/1 were selected. Although synthesis modulation through the addition of monocarboxylic acids is an equally viable route to engineer missing linker defects in UiO‐66, here we sought to avoid potential capping of the Lewis acidic defect sites by these monocarboxylates.3b, 3g Powder X‐ray diffraction (Figure S.1) confirmed the successful preparation of UiO‐66 in both cases. From thermogravimetric analysis of the washed MOFs (Figure S.2), the average number of linkers per inorganic brick was estimated to be 9.9 and 11.6, respectively for the materials prepared at linker/Zr molar ratios of 1/1 and 2/1, hereafter denoted as UiO‐66‐9.9 and UiO‐66‐11.6. In accordance with the higher degree of defectivity in UiO‐66‐9.9, a lower thermal stability is observed for this material as compared to UiO‐66‐11.6. Nitrogen physisorption isotherms for both materials are presented in Figure S.3. From these, Brunauer‐Emmett‐Teller specific surface areas were determined to be 1090.0 m² g⁻¹ for UiO‐66‐9.9 and 1177.7 m² g⁻¹ for UiO‐66‐11.6.

Prior to reaction, both ethanol‐exchanged UiO‐66 samples were activated either at 150 °C in air for 24 h, to remove physisorbed guests, but retain the hydrated state of the inorganic brick; or at 280 °C for 24 h yielding dehydrated, evacuated frameworks. These samples were subsequently tested as catalysts in the Oppenauer oxidation of prenol with furfural (Figure 7). As expected, the more defective UiO‐66‐9.9 shows an overall higher activity than UiO‐66‐11.6, owing to an increased number of coordinatively unsaturated Zr sites, regardless of the hydration state of the framework. The latter however has a significant impact on the activity of the UiO‐66 material. For both tested MOFs, the hydrated inorganic bricks yield higher prenol conversions, reminiscent of the case of hydrous zirconia,13, 14 even though the hydrated materials are expected to have a lower density of Lewis acidic sites (see Figure 4), once again highlighting the importance of the cooperative effect between Zr sites and μ₃‐OH groups. Rather surprisingly, despite having only a limited amount of defects, UiO‐66‐11.6 still shows significant activity in the prenol Oppenauer oxidation, reaching prenol conversions of 64 % and 68 % for the dehydrated and hydrated materials after 24 h, respectively.

Figure 7.

Conversion profiles of prenol in the Oppenauer oxidation with furfural, using UiO‐66–9.9 (red) and UiO‐66‐11.6 (black) as catalyst (hydrated UiO‐66 as closed circles, dehydrated UiO‐66 represented with open triangles). 50 mg catalyst, prenol/Zr=10, Furfural/Zr=20, toluene, 120 °C, nonane internal standard.

Conclusions

The MPVO reaction comes out as an ideal tool to explore the amphoteric nature of the defective UiO‐66 material. Open active sites appear on the Zr‐O‐Zr surfaces between coordinatively unsaturated Zr‐atoms resulting from removal of the BDC linker. It has been shown that the catalytic activity is spread out over the Zr‐O‐Zr site with a Lewis acid center at the under‐coordinated Zr‐atoms and a Brønsted site on the μ₃‐oxygen. The presence of acid and base centers within molecular distances has been shown to be essential in the performance of the catalytic reaction as they cooperate in a concerted way during the chemical transformation. The importance and effectiveness of a bifunctional catalyst cannot be overestimated. An advantage of the UiO‐66 material is that it can easily be tailored: chemical properties are dependent on the synthesis conditions, post‐synthetic treatments, etc. All mechanistic studies on the UiO‐66 material merely focused on the Lewis acidity of the coordinatively unsaturated sites. In this work we show that there exists a subtle interplay between the Lewis acid sites and the Brønsted base sites (oxo‐atoms). The basicity can be tuned to a large extent by the pretreatment of the material. Hydrated bricks have stronger basic sites and facilitate protonation steps in dual catalyzed reactions on the other hand in subsequent deprotonation steps the opposite behavior is observed. To support the theoretical hypothesis, new experiments were performed on UiO‐66 of different defectivity and in which the materials were either hydrated or dehydrated. We systematically found for the hydrated materials a much higher activity in the Oppenauer oxidation of prenol with furfural, in complete agreement with the theoretical predictions.

In the earlier work of Boronat et al.11 a similar oxidation reaction has been studied in Zr‐substituted zeolites. In the Zr‐beta catalyzed MPV reaction of cyclohexanone with 2‐butanol, both reactants are directly coordinated on the same metal center. Deprotonation of the alcohol leads to the formation of an alcoholate intermediate bonded to the Zr‐center but the role of the hydrolyzed Zr‐OH group in the MPV reaction is less deterministic than the hydroxy Zr‐OH‐Zr group in defective UiO‐66 material. In addition, by thermal treatment of the material, the basicity of the oxygen bridging the two Zr‐centers on which the reactants are coordinated, can be tuned, which is not the case in Zr‐beta zeolites.

Another feature which has been revealed here in this work is the remarkable reshuffle of the electronic properties of the inorganic Zr‐brick if protonating an μ₃‐oxygen. This has been demonstrated by studying the stabilization effects induced by a hydrated and/or a dehydrated Zr‐brick on the coordination of alcohols, water, etc. In the dehydrated material the two 6‐fold coordinated Zr‐atoms are only capped by a single oxygen atom, showing a vacancy in the place of the missing oxygen atom. Once the basic oxo‐atom has been protonated—forming a frame hydroxy group—the internal electronic structure of the inorganic brick changes drastically leading to an extra stabilization of some 80 kJ mol⁻¹ to all complexes adsorbed at the hydrated material with respect to those adsorbed on the dehydrated 6‐fold material. On removal of the hydroxy proton the brick restores its internal structure and adsorption properties on both materials become similar with each other.

This work shows the versatile catalytic behavior of defective UiO‐66 materials and their ability to tune their catalytic properties by proper pretreatments.

Experimental Section

All chemicals were obtained from Sigma Aldrich, ABCR GmbH or TCI Europe N.V. and used without further purification. UiO‐66 was synthesized in 250 mL pyrex Schott bottles by dissolving 8.1 mmol of ZrCl₄ (1.89 g) and either 8.1 mmol (1.35 g) or 16.2 mmol (2.70 g) of terephthalic acid in 200 mL of N,N‐dimethylformamide (DMF). To these solutions, 24 mmol of HCl (37 wt % in H₂O; 2 mL) was added, after which the reactor vessel was closed and placed in a preheated oven at 130 °C for 24 h. Following synthesis, the formed UiO‐66 materials were separated from the mother liquor by centrifugation, and washed twice with DMF overnight at 120 °C to remove unreacted linkers. Subsequently, three more solvent exchange steps with ethanol (overnight, 80 °C) were performed, after which the materials were activated at 150 °C for 24 h in air to obtain hydrated UiO‐66 samples, or at 280 °C for 24 h in air to obtain dehydrated UiO‐66 samples. Prior to their use as catalyst, samples were stored in an N₂ atmosphere.

Powder X‐ray diffraction patterns were recorded on a STOE COMBI P diffractometer in Bragg–Brentano geometry employing monochromated Cu_Kα1 radiation (λ=1.54060 Å) equipped with an IP‐PSD detector. Thermogravimetric analyses were performed on a TA instruments TGA Q500. Samples were heated at a 5 °C min⁻¹ rate to 700 °C under an O₂ flow. Nitrogen physisorption isotherms were measured on a Micromeritics 3Flex surface analyzer at 77 K, after evacuating the samples for 4 h at 180 °C under a 10⁻⁴ mbar vacuum. Surface areas were calculated by applying the multi‐point BET method to the isotherm's adsorption branch, taking into account the consistency criteria set forth by Rouquerol.20

Catalytic experiments were performed in 10 mL glass reactor vials, in which 50 mg of activated catalyst was weighed in under an N₂ atmosphere. To each reactor, 10 mL of a solution of prenol (molar ratio 10/1 vs. Zr, as determined from thermogravimetric analysis of the MOFs) and furfural (molar ratio 2/1 vs. prenol) in toluene, with nonane as internal standard (molar ratio 1/1 vs. prenol) was added, and reactions were performed at 120 °C in a heated reactor block under stirring. After centrifugation to remove the solid catalyst, samples were analyzed using gas chromatography (Shimadzu GC‐2010 chromatograph, equipped with an FID detector and a 60 m DB‐FFAP column).

Computational Details

All periodic density functional theory (DFT) calculations have been performed using Vienna Ab Initio Simulation Package (VASP 5.3.5).15 The periodic model, in which the environment of surrounding linkers and other Zr Lewis acid sites is accounted for, has previously been used to give a reliable description of the system. The defective brick has two active sites A and B (see Figure 1). Reactions will be simulated on site A whereas site B is considered as passive. For the simulations, the Brillouin zone was sampled by the Γ‐point as the influence of the chosen k‐point mesh was previously checked.6b We applied gradient corrected PBE16 method for optimization and vibrational analysis including Grimme's D3 dispersion interactions.17 A plane wave kinetic energy cut‐off of 600 eV was used. The convergence criterion for the electronic self‐consistent field problem was set to 10⁻⁵ eV. The thermal corrections were performed on the basis of frequencies obtained with a partial Hessian approach18 using the in‐house developed processing toolkit TAMkin.19

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

J. Hajek, B. Bueken, M. Waroquier, D. De Vos, V. Van Speybroeck, ChemCatChem 2017, 9, 2203.