Figure 2. Illustration and results of the theoretical framework.

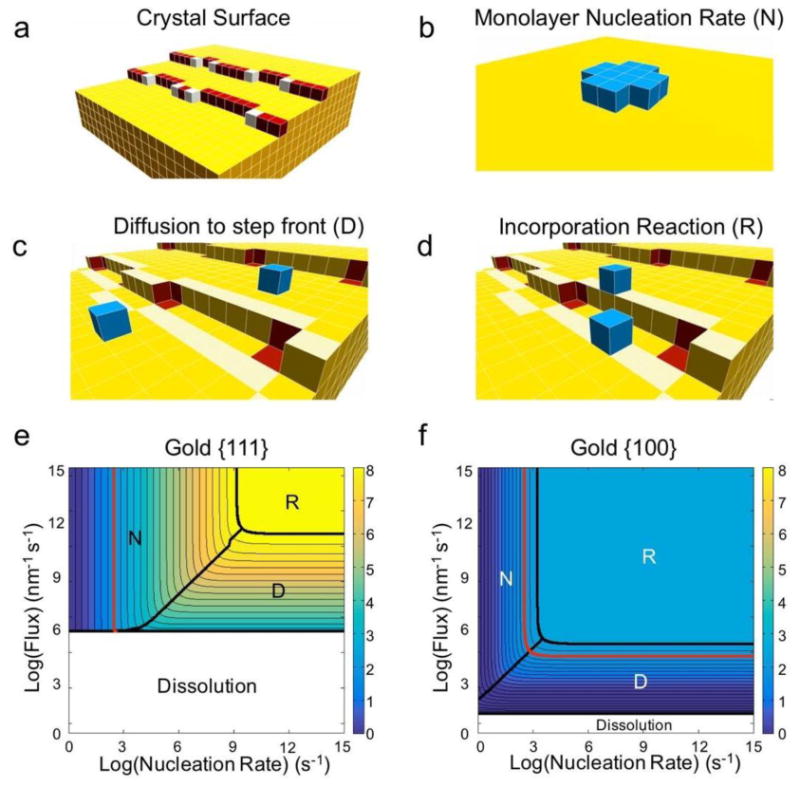
a, Schematic of a crystal facet. The surface is populated by terrace (yellow), step (red), and kink (white) sites. b-d, The three primary processes influencing the growth rate of a crystal facet. b, The monolayer nucleation rate (N) is the rate at which a critical nucleus (blue) – an island of growth units that will continue to grow rather than dissolve – forms on a facet (yellow). c, The “diffusion” rate can refer to different processes in different theories. Here, we define the rate of diffusion (D) specifically as the flux of growth units to the step front – the region of terrace sites that are one jump from step or kink sites (highlighted in light yellow). This definition separates growth unit diffusion from the incorporation reaction process. d, The incorporation “reaction” rate (R) as defined in our treatment is the net rate at which growth units in the step front (highlighted in light yellow) diffuse into kink binding sites (red). The delivery of growth units to kink binding sites is therefore divided into two regimes in our theory: diffusion of growth units to the step front, and incorporation reaction from the step front into the kink binding sites. e-f, Our theoretical framework produces contour plots of facet growth rates that highlight the rate-limiting growth process as a function of experimental conditions for (e) {111} and {f} {100} facets of gold nanoparticles. The red contour denotes the experimental growth rate at which secondary nucleation – the formation of new seeds – occurs. Polyhedra like rods and plates form below this rate.