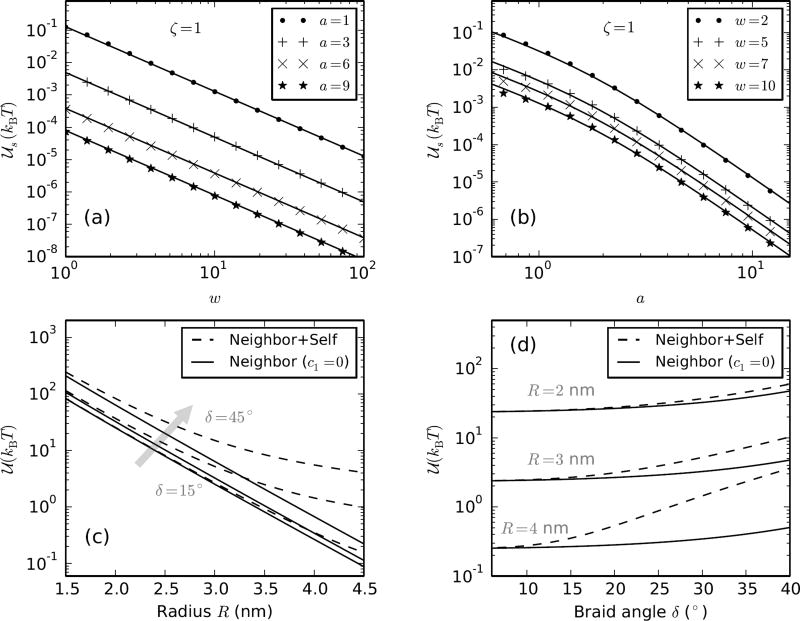
FIG. 6.

(a) Comparison of numerical evaluation (points) of 𝒰_s (Eq. A.3) with the proposed empirical solution (Eq. A.4) (solid lines) with ζ = 1, c₁ = 0.042 and c = 0.312, as a function of w for various values of a = 1, 3, 6 and 9. (b) 𝒰_s versus a for w = 2, 5, 7 and 10 showing that the empirical function is a good fit to the numerical solution. (c) Plot of the total electrostatic potential 𝒰 per unit braid length A (Eq. A.5) with (dashed lines) and without (solid lines) the self interaction component (the second term in Eq. A.5 containing the self interaction can be set to zero by putting c₁ = 0) versus braid radius (R) over a range of braiding angles δ = 15°, 30° and 45° (Table I). We used ζ = 2700 (corresponding to 100 mM Na⁺, Table I), c₂ = 0.312 and c₁ was chosen to be either 0 (only neighbor interaction plot, solid lines) or 0.042 (neighbor and self interaction plot, dashed line). (d) Comparison of the self and the neighbor components of the total electrostatic potential as a function of braiding angle δ for braid radii R = 2, 3 and 4 nm. The self-energy contribution is non-negligible in braids with radii ≳ 3 nm, which is the case ≲ 2 pN at 100 mM salt (Figure 7a).