Fig. 3.

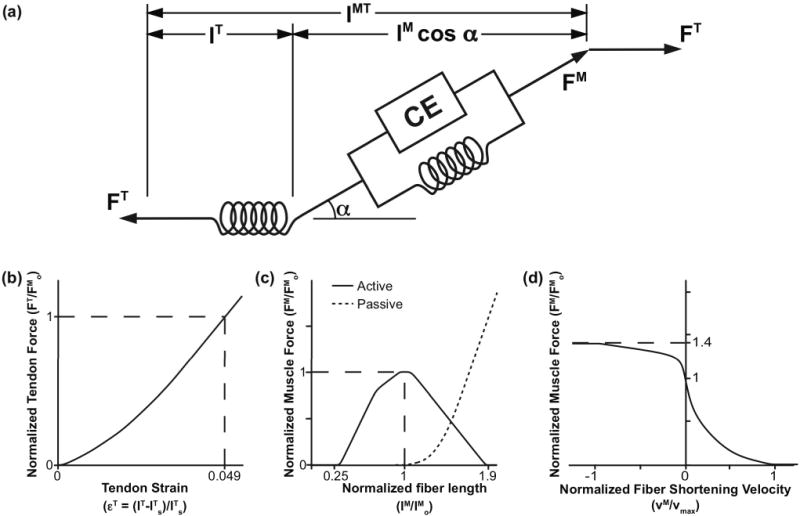
Computational model of muscle-tendon units. Muscles were represented as massless linear actuators with active and passive properties described by scalable generic force-length and force-velocity curves [42]. The generic curves were scaled by five muscle-specific parameters: maximum isometric force (F^M_o), tendon slack length (l^T_s), optimal fiber length (l^M_o), maximum fiber shortening velocity (v_max), and pennation angle at optimal fiber length (α_o). (a) The total muscle-tendon length (l^MT) was a function of the geometric pose of the model. The muscle fiber length (l^M), muscle pennation angle (α), and tendon length (l^T) were determined based on l^MT, muscle activation, and the force equilibrium constraints between the muscle fiber (F^M) and tendon (F^T). (b) Tendon was modeled as a passive series elastic element whose normalized force (F^T/F^M_o) was a function of tendon strain (ε^T). Tendon strain was calculated from the muscle-specific tendon slack length (l^T_s). We assumed a tendon strain (ε^T) of 4.9% [42] when the muscle developed maximum isometric force (F_o^m). (c) Muscle fiber was modeled as an active contractile element (CE) in parallel with a passive elastic element. Active isometric fiber force was a function of muscle activation (a) and fiber length normalized by optimal fiber length (l^M/l^M_o). Passive fiber force was a function of normalized fiber length (l^M/l^M_o) only. (d) Muscle active isometric fiber force was scaled based on fiber velocity (v^M) normalized by maximum shortening velocity (v_max) of the muscle. Total muscle force was calculated as the sum of active and passive fiber force.