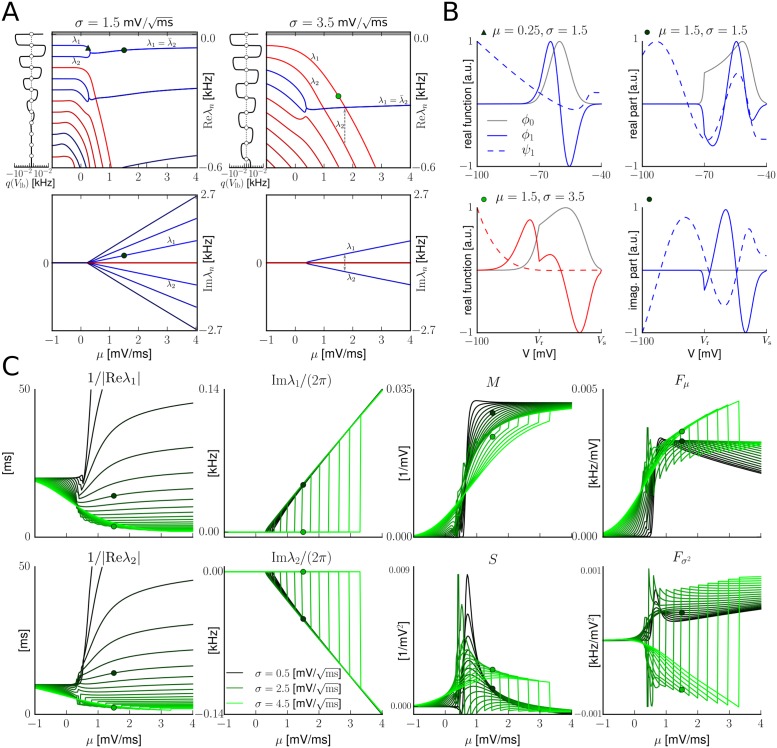
Fig 7. Spectrum of the Fokker-Planck operator $\mathcal{L}$ and related quantities.

A: regular eigenvalues of $\mathcal{L}$ (blue) and diffusive ones (red) with real and imaginary part (top and bottom, respectively) as a function of the mean input μ for small noise intensity σ (left) and larger input fluctuations (right). The first two dominant eigenvalues λ₁, λ₂ are indicated together with discontinuities in the real (λ₂) and imaginary part (λ₁ and λ₂), respectively. The stationary eigenvalue λ₀ = 0 is shown in gray. Note that the value of the mean input μ at which the eigenvalue λ_n changes from real to complex values depends on the noise amplitude σ and the eigenvalue index n which is difficult to see in the figure. The narrow winding curves attached to the left side of the respective spectra represent the lower bound flux q(V_lb) for μ_min = −1.5 mV/ms as a function of (real) eigenvalue candidate λ. The flux axis has a logarithmic scale between the large ticks (absolute values between 10⁻¹⁰ and 10⁻² kHz) and is linear around the dashed zero value. The open circles denote the eigenvalues, i.e., those λ that satisfy q(V_lb) = 0. Note that q(V_lb) ranges over several orders of magnitude. B: stationary eigenfunction ϕ₀ = p_∞ (gray) and nonstationary eigenfunctions ϕ₁ of $\mathcal{L}$ and ψ₁ of ${\mathcal{L}}^{*}$ corresponding to the first dominant eigenvalue λ₁ for three different input parameter values indicated by the triangle and circles in A (same units of μ and σ as therein). The eigenfunctions are biorthonormalized, but (only) for visualization truncated at V = −100 mV and furthermore individually scaled to absolutely range within the unit interval of arbitrary units [a.u.]. C: first and second dominant eigenvalues λ₁, λ₂ with real and imaginary part (that are also indicated in A), as well as additional (real-valued) quantities of the model spec₂ (M, S, F_μ, F_σ²) as a function of input mean μ and noise strength σ in steps of $0.2\text{mV}/\sqrt{\text{ms}}$ from small values (black) to larger ones (green). The dots indicate identical parameter values to the spectra of A and the eigenfunctions of B (darker: $\sigma =1.5\text{mV}/\sqrt{\text{ms}}$, brighter green: $\sigma =3.5\text{mV}/\sqrt{\text{ms}}$).