Single-Molecule Protein Folding Experiments Using High-Precision Optical Tweezers

Summary

How proteins fold from linear chains of amino acids to delicate three dimensional structures remains a fundamental biological problem. Single-molecule manipulation based on high-resolution optical tweezers (OT) provides a powerful approach to study protein folding with unprecedented spatiotemporal resolution. In this method, a single protein or protein complex is tethered between two beads confined in optical traps and pulled. Protein unfolding induced by the mechanical force is counteracted by the spontaneous folding of the protein, reaching a dynamic equilibrium at a characteristic force and rate. The transition is monitored by the accompanying extension change of the protein and used to derive conformations and energies of folding intermediates and their associated transition kinetics. Here, we provide general strategies and detailed protocols to study folding of proteins and protein complexes using optical tweezers, including methods of data analysis to extract folding energies and rates from the single-molecule measurements.

1. Introduction

As one of life’s building blocks, proteins play essential roles in almost all cellular activities. Their functions rely on their structures, stabilities, and dynamics (1). Misfolding of proteins contributes to numerous human diseases (2, 3). Accessing folding stability and kinetics of proteins is crucial for understanding their working mechanisms, functions, and dysfunctions. Various experimental approaches have been developed to study protein folding (4–6). They differ in the proteins of interest and ways to induce protein unfolding and to detect subsequent folding. Despite great efforts, measuring membrane protein folding and stabilities remains challenging (6). Thus, we focus on soluble proteins here. One of the first and main challenges for protein folding studies is to unfold proteins. Some proteins or protein domains are marginally stable in solution, whose folding and stabilities can directly be probed by NMR and/or hydrogen-deuterium exchange (5, 7). However, most proteins are very stable and rarely unfold spontaneously due to thermal fluctuation, making it difficult to observe protein folding. In addition, when proteins do unfold this way, many of them refold so rapidly (within one millisecond) that it is difficult to accurately follow their folding kinetics. To overcome these difficulties, proteins are often destabilized by chemical denaturants such as urea and guanidine chloride (8), temperature jumps (9), or pressure and pH changes (10). These methods also slow down protein folding, facilitating its detection. Once proteins are unfolded, their synchronized folding kinetics can be monitored by various spectroscopic techniques (4), such as circular dichroism (8), fluorescence (11), absorbance, Raman scattering (12). These approaches have greatly contributed to our understanding on protein folding. However, these ensemble-based approaches share several weaknesses. They require synchronization of proteins in the unfolded states and often lack sufficient resolution to resolve multiple folding intermediates. Moreover, the denaturing environment makes it impossible to study protein folding regulated by other proteins, an important aspects of protein folding in vivo (13, 14).

Optical tweezers force microscopy is a unique tool to study protein folding (15–17). OT use optical traps to confine micron-sized beads in harmonic potentials as a force and displacement sensor (18–20). A protein is attached to the surface of a trapped bead at one end and to a second surface at another end (15). The latter surface can be provided by a microscope glass slide or by another bead in a different optical trap or sucked to the tip of a micropipette. The protein is pulled by separating the two surfaces or protein attachment sites. The pulling force and the extension of the protein accompanying its folding and unfolding transition are derived from displacements of the beads in optical traps. The displacement is typically measured by an optical interference method called back-focal plane interferometry (21). The method can achieve sub-angstrom spatial resolution and better than ~10 μs temporal resolution (22, 23). However, the resolution of optical tweezers is limited by Brownian motion of the beads in optical traps, leading to typically 0.2–0.4 nm spatial resolution (22, 24–26). To achieve such high resolution, two optical traps are used to completely suspend the dumbbell formed by two beads connected by a single protein, which maximally decouples force and extension measurements from environmental noise sources, such as stage drift, and laser pointing fluctuations (22, 24). In addition, a protein molecule can be held at constant force to observe its folding and unfolding transitions for more than an hour (15, 19, 27, 28). The extremely large dynamic range of measurements make it possible to pinpoint multi-scale protein folding in real time among many distinct intermediate states with large energy differences.

The application of optical tweezers to folding studies of macromolecules was pioneered by Bustamante and co-workers (15, 16, 29). Since 1997, optical tweezers have been used to measure folding energies and kinetics of numerous proteins or protein complexes, including RNase H (15), Von Willebrand factor (30), T4 lysozyme (31), GCN4 leucine zipper (28, 32), calmodulin (33, 34), and prion proteins (35). In this work, we will describe the basic strategies and protocols to study protein folding using two membrane fusion protein complexes, the human immunodeficiency virus type 1 (HIV-1) glycoprotein 41 (gp41) complex (36) and the synaptic soluble N-ethylmaleimide-sensitive-factor attachment protein receptor (SNARE) complex (27, 37) as examples. Both complexes thermodynamically couple their concurrent folding and assembly to membrane fusion (38, 39). In this process, the fusion proteins generate large forces to draw two membranes into proximity to merge. In particular, the synaptic SNARE complex mediates fusion of neurotransmitter-containing synaptic vesicles to pre-synaptic plasma membranes at nerve endings, leading to neurotransmitter release (38). The released neurotransmitters can elicit action potentials in the postsynaptic neurons at synaptic junctions or lead to contraction of muscles at neuromuscular junctions. The gp41 complex mediates fusion between viral and host cell membranes, the first step leading to HIV infection (39, 40). Both fusion protein complexes assemble in a step-wise manner, generating many intermediates (13, 27, 36, 40). The SNARE folding intermediates can serve as targets for other regulatory proteins to control membrane fusion, for example, calcium-triggered synaptic vesicle fusion (38). In contrast, gp41 folding intermediates can be targeted by various fusion-inhibitors to inhibit gp41 folding, thereby blocking HIV infection (36). Therefore, optical tweezers are a perfect tool to measure the force and energy generated by fusion proteins and their folding intermediates and kinetics.

In the following, we will first describe our experimental setup and the protein and DNA constructs required to pull single proteins. Then we will provide the protocols to prepare the protein and DNA samples and conduct single-molecule experiments using optical tweezers. Finally, we will outline our methods of data analysis.

2. Materials

2.1 Protein expression and purification

1. BL21 Gold (DE3) competent cells (Agilent Technologies).

2. LB medium: Dissolve 25 g LB broth (Miller) into 1 L ddH₂O, autoclave for 30 min.

3. SOC medium (Sigma): 20 g/L tryptone, 5 g/L yeast extract, 4.8 g/L MgSO₄, 3.603 g/L dextrose, 0.5g/L NaCl, 0.186 g/L KCl.

4. IPTG stock solution (1000 ×): Dissolve 2.38 g IPTG powder in 10 mL ddH₂O to make 1 M stock solution. Filter the solution with 0.22 μm syringe filter.

5. Kanamycin stock solution (1000 ×): Dissolve 1.5 g kanamycin powder into 30 mL ddH₂O to make 50 mg/mL solution and filter with 0.22 μm syringe filter.

6. Selective LB plate: Dissolve 25 g LB broth (Miller) and 15 g Agar into 1 L ddH₂O. Autoclave for 30 min. After autoclaving, cool to approximate 55 °C and add 1 mL kanamycin stock solution (50 mg/mL) to final concentration of 50 μg/mL, and pour into petri dishes.

7. Lysis buffer: 25mM HEPES (pH 7.7), 400 mM KCl, 0.5 mM TCEP, 10% glycerol, 10 mM imidazole.

8. Needles: 18G × 1 needle (1.2mm×25mm) and 23G× 1 needle (0.6 mm × 25 mm) (BD precision gliding needle)

9. Protease inhibitor cocktail tablet, cOmplete, EDTA free (Roche)

10. Nickel beads: Ni Sepharose 6 Fast Flow (GE healthcare Lifesciences)

11. Wash buffer I: 25mM HEPES, pH 7.7, 400 mM KCl, 0.5 mM TCEP, 10% glycerol, 30 mM imidazole.

12. Wash buffer II: 25mM HEPES, pH7.7, 400 mM KCl, 0.5 mM TCEP, 10% glycerol, 50 mM imidazole.

13. Elution buffer: 25 mM HEPES, 200 mM potassium glutamate, 300 mM imidazole.

14. Amicon (or Centricon, EMD Millipore)

2.2 Protein biotinylation in vitro

1. BirA biotin ligase (3 mg/ml, Avidity)

2. Biomix-A (10 × concentration: 0.5 M bicine buffer, pH 8.3, Avidity)

3. Biomix-B (10 × concentration: 100 mM ATP, 100 mM MgOAc, 500 μM d-biotin, Avidity)

4. Additional d-biotin (10 × concentration: 500 μM, Avidity)

5. NuPAGE Novex 4–12% Bis-Tris precast protein gels (Thermo Fisher)

6. 4 × SDS loading buffer (Thermo Fisher)

7. Streptavidin (1mg/1ml): Add 1 ml ddH₂O to 1 mg streptavidin powder (Promega).

8. SDS-PAGE Coomassie staining solution: 0.1–0.2 g Coomassie G-250, 225 mL methanol, 225 mL H₂O, 50 mL glacial acetic acid.

9. SDS-PAGE Coomassie de-staining solution: 150 mL methanol, 300 mL ddH₂O, 50 mL glacial acetic acid.

2.3 DNA handle

1. Taq DNA polymerase with ThermoPol buffer (NEB)

2. dNTP mix (10 mM, Invitrogen)

3. PCR purification kit (Qiagen)

4. PureLink PCR Purification Kit (Invitrogen)

2.4 Chemical crosslinking

1. Buffer A (0.1 M sodium phosphate buffer, pH 5.8, 400 mM NaCl)

2. Buffer C (0.1 M sodium phosphate buffer, pH 8.5, 400 mM NaCl)

3. 10 mM 2,2′-dithiodipyridine disulfide (DTDP) stock solution: Dissolve 11 mg DTDP powder into 1 mL acetonitrile and then add 4 mL ddH₂O to dilute to 10 mM.

4. Bio-spin columns (Bio-RAD, Micro Bio-spin 6 columns)

2.5 Single-molecule experiments on optical tweezers

1. Phosphate-buffered saline (PBS): 137 mM NaCl, 2.7 mM KCl, 8.1 mM Na₂HPO4, 1.8 mM KH₂PO₄, pH 7.4.

2. Catalase from bovine liver: aqueous suspension, 10000~40000 units/mL (Sigma-Aldrich).

3. Glucose oxidase from Aspergillus niger: 120 mg/mL, ≥100 units/mg (Sigma-Aldrich).

4. PBS buffer with oxygen scavenging system: Add 75 μL glucose (10% w/v), 6 μL glucose oxidase (0.75 units/μL), and 4.7 μL catalase (30 units/μL) to 3 ml PBS.

5. Polystyrene beads: 1% w/v anti-digoxigenin antibody coated polystyrene particles (2.1 μm, called DIG beads), streptavidin-coated polystyrene particles (1.8 μm), both from Spherotech, IL.

6. Customized glass tubing (King Precision Glass, Inc., CA): Bead dispenser tubes with 100 μm outer diameter (OD) and 25 μm inner diameter (ID); protein injection tube with 80 μm OD and 40 μm ID.

7. Slides: Microscope cover glass (60 × 24 × 0.17 mm) (Fisherbrand)

8. Plastic tubing: Polyethylene tubing PE10, PE50 (Becton Dickinson)

9. Nescofilm (Karlan research)

10. Sodium azide: Make 0.02% sodium azide solution and filter with 0.22 μm syringe filter.

3. Equipment

Dual-trap high-resolution optical tweezers

The dual-trap optical tweezers are home-built and calibrated as previously described (24, 26, 27). Briefly, a 1064 nm laser beam is expanded, collimated, and split into two orthogonally polarized beams. One beam is reflected by a mirror attached to a nano-positioning stage that could tip/tilt in two axes (Mad City Labs, WI). The two beams are then combined, further expanded, and focused by a water-immersion 60X, N.A. 1.2 objective (Olympus, PA) to form two optical traps (Fig. 4A). One trap can be moved by turning the mirror and the other trap is stationary. The outgoing laser beams are collimated by a second objective, split again by polarization, and projected to two position-sensitive detectors (Pacific Silicon Sensor, CA) to detect bead positions using back-focal-plane interferometry. The force constants of both optical traps are determined by Brownian motion of the trapped beads before each single-molecule experiment (41). The force, extension, trap separation, and other experimental measurements were acquired at 20 kHz, filtered online to 10 kHz, and stored on hard-disk.

Fig. 4.

Microfluidic chamber used in optical trapping experiments. (A) Microfluidic chamber installed on a motorized translational stage and positioned between two objectives. The PE tubing connected to the three channels and to the protein tube can be seen. (B) Microfluidic chamber installed on the chamber frame. (C) Microfluidic chamber showing three channels, two dispenser tubes, and the protein tube. The thickness of channels between two coverslips is around 180 μm. (D) Diagram illustrating how the microfluidic channel is assembled onto the frame. The figure is reproduced from our earlier work with permission (41).

Laser engraver

Epilog Zing laser engraving and cutting system. Used to cut holes in coverslips and to cut Nescofilms into patterns to form the microfluidic chamber.

4. Experimental Methods

4.1 Basic experimental setup to pull a single protein

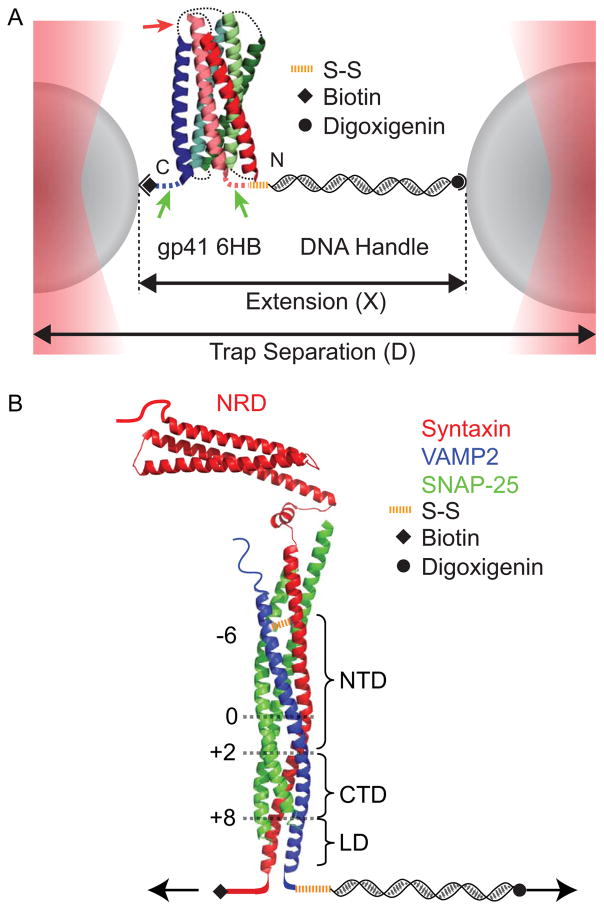
We used dual-trap high-resolution optical tweezers to pull a single protein complex (Fig. 1). The protein molecule was attached to two polystyrene beads via one or two DNA handles that were covalently crosslinked to the protein by disulfide bonds (15). Given the small size of a typical protein (a few nanometers) compared to the diameters of the beads (~ 2 μm), the handle is essential for separating the two bead ‘walls’ to facilitate the protein attachment and the accurate measurement of bead displacements. For this purpose, the total handle length typically ranges from 500 base pairs to a few thousand base pairs. Longer DNA handles reduce the signal-to-noise ratio of the detected protein transitions due to compliance of long handles (42). In addition, long handles are difficult to make in the molar amount that is sufficient to efficiently crosslink the handles to proteins. To facilitate specific attachment, two different beads are used, one coated with streptavidin and the other coated with anti-digoxigenin antibody. Correspondingly, the DNA handles and/or the protein are labeled with biotin and digoxigenin moieties. For simplicity, we typically use one 2,260 bp DNA handle in our pulling experiments (27, 28, 36, 43). The DNA handle is labeled with two digoxigenin moieties at one end and a thiol group at another end. The handle is crosslinked to a unique cysteine residue on the surface of the protein. The protein contains a biotin moiety that is used to directly immobilize the protein to the streptavidin-coated bead. We do not found any significant nonspecific interaction between the proteins and the bead surfaces (43). Thus, folding energy and dynamics of the protein is not affected by its immobilization to the bead surface. Once tethered between two bead surfaces, the protein molecule was pulled by moving one trap away from the other at a constant speed, typically 10 nm/sec, or holding the protein at a constant trap separation or mean force.

Fig. 1.

Experimental setup to pull a single protein complex using dual-trap high-resolution optical tweezers. (A) A single gp41 complex in a fully folded six-helix bundle conformation is tethered between two polystyrene beads via a 2,260 bp DNA handle and pulled by increasing the trap separation (36). The extension and tension of the protein-DNA tether are detected. (B) SNARE construct used to measure the energetics and kinetics of SNARE assembly using optical tweezers (13). A fully assembled cytoplasmic synaptic SNARE complex is pulled from the C-termini of syntaxin and VAMP2 while crosslinked at the N-termini near the −6 layer. The SNARE complex consists of the N-terminal domain (NTD), the C-terminal domain (CTD), the linker domain (LD), and the N-terminal regulatory domain (NRD) in syntaxin. The positions of different layers are indicated by black numbers.

4.2 Protein constructs

We will use the two fusion proteins to demonstrate two complementary methods to study coupled folding and assembly of protein complexes. Once a protein complex unfolds, its different protein subunits will be pulled apart, making the folding process irreversible. To facilitate reversible protein folding for energy measurements, we will covalently link the different subunits in a complex. The linkage has to be designed to allow functional folding of the complex and may vary between protein complexes. For this reason, we fuse three gp41 proteins into a single polypeptide and use a disulfide bond to crosslink two SNARE proteins in a SNARE complex (13, 36, 37).

Gp41 protein

The gp41 complex is a homotrimer that forms a six-helix bundle (44) (Fig. 1A). Each gp41 monomer contains an N-terminal heptad repeat (NHR), a loop, and a C-terminal heptad repeat (CHR), which form a helical hairpin. In the six-helix bundle, the three NHRs associate into a central three-helix bundle, while the three CHRs bind its grooves in an anti-parallel fashion. To characterize the folding/unfolding of a single gp41 complex, we joined the three gp41 hairpins with 6 amino acid flexible linkers to a single polypeptide. In addition, we added a cysteine residue followed by a spacer sequence (CGGSGGSKGGSNG) to the N-terminus of the tandem gp41 sequences and an AviTag sequence (GLNDIFEAQKIEWHE) following another spacer sequence (GGNSGDYKDDDDKGSGGSGNGGSGDSLEFIASKLAG) at the C-terminus. The AviTag sequence can be recognized by the biotin-ligase BirA and specifically labeled by biotin on the lysine residue. The spacer sequence before the AviTag is used to facilitate the enzymatic biotinylation by minimizing possible steric hindrance of the gp41 six-helix bundle to BirA binding to the AviTag. In addition, the spacer allows the gp41 protein to stay away from the bead surface in the presence of force, preventing nonspecific interactions between the gp41 protein and the bead surface. Finally, we mutated the natural cysteine residues in the loop of the gp41 monomer to serine, because they would compete with the N-terminal cysteine for crosslinking to the DNA handle, and thereby change the pulling site on the protein. Other proteins may contain functionally important cysteine residues on their surfaces. Thus these cysteine residues cannot be removed. In this case, alternative protein labeling methods such as the CoA-based method and click chemistry (45, 46) can be employed to conjugate the protein to the DNA handle.

SNARE protein complex

The fully assembled synaptic SNARE complex comprises three proteins: syntaxin, SNAP-25, and VAMP2 (also called synaptobrevin) (47) (Fig. 1B). They form a parallel four-helix bundle, with SNAP-25 contributing two helices. Along the spine of the bundle are 15 layers (numbered from −7 to −1 at the N-terminus and from +1 to +8 at the C-terminus) of hydrophobic amino acids and one layer (“0” layer) of hydrophilic amino acids consisting of three glutamine and one arginine (48). The helices of syntaxin and VAMP2 further extend into the linker domain (LD) and the transmembrane domain to form a two-stranded coiled coil at their C-termini (49). Before membrane fusion, syntaxin and SNAP-25 are located on the target plasma membrane and partially fold into a binary t-SNARE complex, while VAMP2 is anchored on the vesicle membrane (thus called v-SNARE) and is mainly disordered. During membrane fusion, the t- and v-SNAREs first pair at their membrane distal N-termini and then zipper towards their membrane-proximal C-termini to drive membrane fusion. To facilitate reversible folding/unfolding of the SNARE complex, we crosslink the N termini of syntaxin and VAMP2 by a disulfide bridge at the −6 layer and pull the complex from their C-termini (13). The SNAP-25 molecule is not covalently joined to other SNARE proteins and can dissociate when the SNARE complex is completely unfolded (27).

After individual SNARE proteins are purified, the ternary SNARE complexes are formed by mixing syntaxin, SNAP-25 and VAMP2 proteins in a molar ratio of 0.8:1:1.2 in 25 mM HEPES, 400 KCl, 5 mM TCEP, pH 7.7 and then incubating the mixture at 4 °C overnight (27). Formation of the ternary complex was confirmed by SDS polyacrylamide gel electrophoresis, because the SNARE ternary complex is SDS resistant. The SNARE complex is purified using the His-Tag on the SNAP-25 molecule. TCEP was also removed during this purification step. SNARE protein was eluted using 0.1 M phosphate buffer containing 0.2 M NaCl and 0.3 M imidazole at pH 8.5.

4.3 Protein expression and Purification

Once the amino acid sequences of the protein constructs have been designed, their corresponding gene sequences can be optimized for expression in bacteria, chemically synthesized, and inserted into an expression vector. We typically inserted the gene into a pET SUMO expression vector (Invitrogen, CA). The vector will add a His-tag followed by a small ubiquitin-like modifier (SUMO) protein domain to the N-terminus of the protein of interest. After purification, this N-terminal addition can be cleaved by SUMO protease.

In this section, we will describe how the recombinant gp41 construct is purified from E. Coli. The gp41 gene has been cloned into the pet SUMO plasmid vector. The SNARE proteins are purified in similar fashion.

Transformation

We transform the above plasmid into the BL21 Gold (DE3) competent cells for gp41 expression.

1. Mix 30 μL of BL21 Gold (DE3) competent E. coli with 10–50 ng plasmid by gently tapping the tube. Avoid pipetting up and down.

2. Incubate on ice for 30 min.

3. Heat-shock the cells at 42°C for 30 seconds.

4. Immediately transfer the competent cells to ice and wait for 2 minutes.

5. Add 200 μL of the S.O.C. medium at room temperature and shake at 37 °C for one hour.

6. Spread 100 μL of the competent cells evenly on a selective LB plate containing 50 μg/ml kanamycin pre-warmed to 37 °C.

7. Incubate at 37 °C overnight.

Protein expression

We usually grow 1 L bacterial culture for protein purification. Depending on the expression level of the protein, one may need to adjust the culture volume.

1. Pick a single colony from the plate and re-suspend it in 100 ml LB with 50 μg/ml kanamycin. Grow overnight at 37 °C while shaking. This is the pre-culture sample.

2. Decant the pre-cultured bacterial sample into 1 L LB with 50 μg/ml kanamycin and grow the culture until mid-logarithmic phase (OD₆₀₀=0.6~0.8).

3. Induce expression of the gp41 protein by adding IPTG to a final concentration of 1 mM.

4. Grow the cells by shaking the culture in the presence of IPTG for 3 to 5 hours at 37 °C. Too short or too long culture time may reduce the amount of protein expression.

5. Harvest the cells by centrifuging the culture at 4500 rpm for 15 min at 4 °C. Discard the supernatant and collect the pellet. The cells can be stored at −20 °C after adding glycerol (10% w/v).

Protein purification

The purification is carried out on ice or in the cold room (4 °C) unless stated otherwise.

1. Thaw the cell pellet for 15 min on ice. Re-suspend cells in 30 ml lysis buffer, in which one tablet of protease inhibitor cocktail has been dissolved. Pipette up and down.

2. Homogenize cells. Using a 30 mL syringe, pass the cell suspension first through a 18G × 1 needle and then through a 23G× 1 needle. This breaks cell aggregates that may block the cell disruptor used in the next step.

3. Disrupt cells using a French press strategy. Pass the cell suspension through the cell disruptor 4~5 times until the suspension becomes clear.

4. Centrifuge the cell suspension at 40,000 rpm for 1 hour at 4 °C to precipitate the cellular debris. Save the clarified supernatant and store on ice.

5. Wash Ni-NTA beads. For 1 L E. coli culture, take 600 μL of Ni-NTA beads from the stock solution and add to 8 mL lysis buffer. Centrifuge at 2000 rpm for 3 min. Discard the supernatant and repeat the washing step three times. Last, suspend the washed beads in 1 mL lysis buffer.

6. Add the Ni-NTA beads to the supernatant from step 4 and rotate the bead solution at 4 °C for two hours to allow gp41 to bind to the Ni-NTA beads.

7. Centrifuge the Ni-NTA beads at 2000 rpm for 5 min at 4 °C. Collect the protein-bound Ni-NTA beads at the bottom.

8. Wash the beads with wash buffer I (WBI) three times. For each wash, re-suspend the Ni-NTA beads with 10 ml WBI by pipetting up and down. Rotate the bead solution at 4 °C for 10–15 min. Centrifuge to collect the Ni-NTA beads.

9. Wash the Ni-NTA beads with wash buffer II (WBII) three times as in step 8.

10. Add 1 mL elution buffer to the Ni-NTA beads and rotate the beads at 4 °C for over 30 minutes to dissociate gp41 from the beads.

11. Centrifuge the bead solution and save the supernatant. Run SDS PAGE to check the protein quality and concentration. Use Amicon to concentrate the protein to a final concentration of 4 mg/ml.

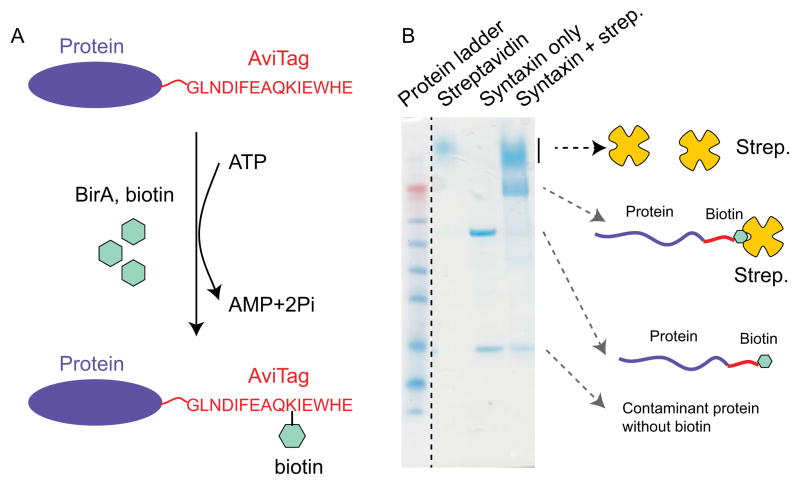
4.4 Protein biotinylation in vitro (Fig. 2A)

Fig. 2.

Enzymatic protein biotinylation. (A) Diagram showing the biotinylation reaction catalyzed by BirA biotin ligase. It recognizes the 15 amino acid AviTag (red) and conjugates biotin to the lysine residue in the presence of ATP. (B) SDS gel electrophoresis to test the yield of protein biotinylation.

Biotinylation, SUMO cleavage, and purification

The following protocol is slightly modified from the biotinylation kit provided by Avidity.

1. Prepare the following biotinylation reaction:

   • AviTag containing gp41 in elution buffer: 420 μL (with1.6 mg gp41)

   • Biomix-A (10 x): 60 μL

   • Biomix-B (10 x): 60 μL

   • d-biotin (10 x): 60 μL

   • BirA enzyme: 4 μL (12 μg)

2. Perform the biotinylation at 4 °C overnight. After the biotinylation reaction is complete, we purify the biotinylated protein from BirA and remove the free biotin by performing the following steps 3–6.

3. Dilute the biotinylated protein solution from step 2 (604 μL) with 3.4 mL lysis buffer to reduce the imidazole concentration to <50 mM. Incubate the diluted protein solution with 500 μL washed Ni-NTA beads by rotating at 4 °C for 2 hours to bind the biotinylated gp41 protein back to the Ni-NTA beads.

4. Wash the Ni-NTA beads with lysis buffer three times to remove free biotin. At this step, one may save 10–20 μL beads and elute gp41 from the beads using 10–20 μL elution buffer to test the biotinylation efficiency with SDS-PAGE (see the following step).

5. Re-suspend the Ni-NTA beads in 500 μL lysis buffer and add 20 μL 3 mg/ml SUMO protease to cleave the SUMO tag. Rotate at 4 °C overnight. Note that imidazole in a high concentration inhibits the cleavage reaction, thus ensure that imidazole concentration is < 50 mM, as in lysis buffer.

6. Precipitate the beads by centrifuging the bead solution at 2000 rpm for 3 min. Save the supernatant containing the final biotinylated and purified gp41. The purified protein can be stored at −80 °C after adding glycerol to 10%.

Check biotinylation level (Fig. 2B)

We test the purity, yield, and biotinylation level of the purified protein using SDS polyacrylamide gel electrophoresis (PAGE). To distinguish the biotin-labeled and unlabeled protein molecules, we bind all the biotinylated protein molecules to streptavidin and then run the SDS gel. Streptavidin is SDS resistant and tightly binds biotin on the protein gel even in the presence of SDS. Thus, the biotinylated protein molecules migrate differently from unlabeled protein molecules. The detailed protocol is listed below.

1. Prepare three 20 μL protein samples (a, b, c) in the SDS loading buffer containing 2 mM TCEP and the follow proteins:

   1. Streptavidin (6 μg)

   2. Streptavidin (6 μg) and biotinylated protein (2 μg)

   3. Biotinylated protein (2 μg)

      Incubate the samples at room temperature for 5–10 min.

2. Load the sample to a protein SDS gel and run the gel at 200 V for 35 min.

3. Stain the protein gel with Coomassie blue by microwaving the gel immersed in the Coomassie blue staining solution for 2 minutes.

4. De-stain the gel by microwaving the gel in de-staining solution for 2 minutes, then shaking in fresh de-staining solution at room temperature for 2 hours.

Figure 2B shows the gel to test the biotinylation level of syntaxin. Comparing the two lanes for the syntaxin with and without streptavidin, one finds that the band corresponding to free syntaxin nearly disappears in the presence of streptavidin, while a new band with higher molecular weight appears. This new band results from streptavidin-bound syntaxin molecules. The comparison reveals that the syntaxin molecules are approximately 100% biotinylated, which is the typical biotinylation yield for soluble proteins. In general, a protein with a biotinylation yield over 50% can efficiently be tethered between two beads in our single molecule experiments. The protein molecules that are not biotinylated cannot form tether between two beads, and thus cannot be pulled.

4.5 DNA handle preparation

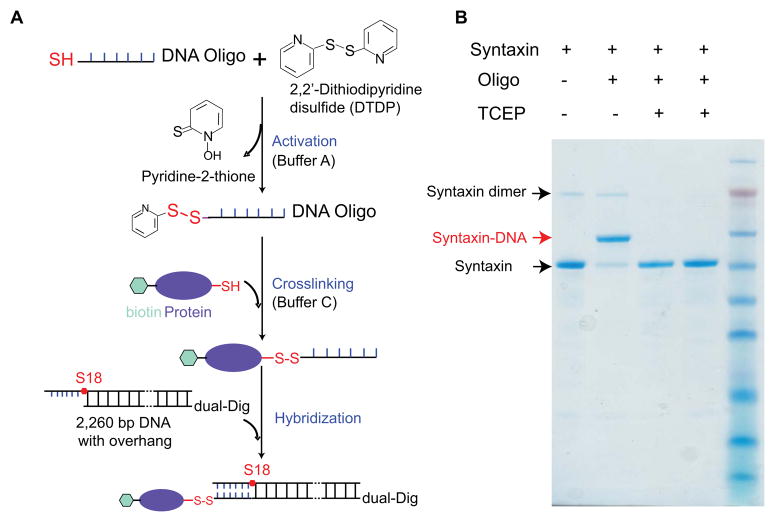
Two types of DNA handles have been used to pull proteins. One type of DNA handles has two blunt ends (Fig. 1A), one with a thiol group and the other with digoxigenin or biotin moieties. The DNA handle is directly crosslinked to the cysteine residue on the protein through the thiol group. The other type of DNA handles contains a 20–30 nucleotide overhang at one end so that it can hybridize with its complementary oligonucleotide (23, 33, 50) (Fig. 3A). The other end of the DNA handle is again blunt and labeled with digoxigenin or biotin moieties. In this case, the protein is first crosslinked to the oligonucleotide and then the DNA handle is hybridized to the oligonucleotide through the overhang. The DNA duplex formed between the oligonucleotide and the overhang is strong enough to hold more than 30 pN for extended time periods required for protein folding studies (>20 minutes). The yield of the crosslinking reaction depends on the molar concentrations of both protein and DNA molecules. The concentration of the long DNA handle generally does not exceed 80 nM, leading to relatively low crosslinking efficiency if the handle is directly crosslinked to the protein. We partially overcome the issue by increasing the protein concentration, typically with over 50:1 protein to DNA molar ratio in the crosslinking reaction. The excess of protein can be removed by first binding the DNA molecule to the bead. In contrast, the oligonucleotide can be synthesized in high concentrations (>100 μM). As a result, nearly 100% protein molecules can be crosslinked to the oligonucleotides (Fig. 3B).

Fig. 3.

Protein-DNA crosslinking. (A) Reaction schemes to crosslink a DNA oligonucleotide to the protein and attach the protein to a long DNA handle by hybridization. (B) SDS gel electrophoresis to test the yield of protein-oligonucleotide crosslinking.

DNA handle with blunt ends

The dsDNA handle typically used in our single-molecule experiments is 2,260 bp in length and contains a thiol (-SH) group at one end and two digoxigenin moieties at the other end. Both labels are added to the 5’ ends of the PCR primers during synthesis. We found that two digoxigenin moieties are required to strongly attach the DNA handle to anti-digoxigenin antibody coated polystyrene beads.

DNA handle with an overhang

The DNA handle contains a 30 nucleotide overhang at one end and either two digoxigenin moieties or one biotin moiety at the other end. The overhang is again introduced through the PCR primer. To prevent polymerase extension to the overhang region, the overhang is attached to the 5’-end of the primer through an 18-atom hexa-ethyleneglycol spacer (S18 from IDT) (Fig. 3A).

Forward primer containing overhang (61 nt):

• C GCC TGC GTA GGA TAT CGC AGA TAC CGC ATC AGT CCA S18 TCT AAG TGA CGG CTG CAT ACT AAC (The overhang sequence is underlined)

Reverse primer:

• Dual-Dig-ATC CAG TAA TGA CCT CAG AAC TCC

• Oligonucleotide complementary to the overhang (40 nt):

  TGG ACT GAT GCG GTA TCT GCG ATA TCC TAC GCA GGC GTT T-Thiol

PCR reaction

For 50 μL reaction:

• ThermoPol buffer (10 ×): 5 μL

• dNTP mix (10 mM): 1 μL

• Forward primer (100 μM): 0.5 μL

• Reverse primer (100 μM): 0.5 μL

• DNA template (Lambda DNA, NEB): 20 ng

• Taq DNA Polymerase: 0.5 μL

• H₂O: Add to final volume of 50 μL

PCR reaction program

1. 95 °C for 3 min

2. 95 °C for 30 s

3. 55 °C for 40 s

4. 65 °C for 2 min (1 kb per min)

   Repeat 2–4 for 32 cycles

5. 72 °C for 5 min

After PCR, use PureLink PCR Purification Kit (Invitrogen) to purify the PCR product. Note that this kit is required to remove the primer with a long overhang from the PCR product.

4.6 Protein and DNA handle crosslinking

Here we show our protocol to directly crosslink the DNA handle or the oligonucleotide (called DNA below) to proteins, which is adapted from Cecconi and coworkers (15, 51, 52).

1. Reduce the DNA and protein by treating them with 2 mM TCEP at room temperature for 1 hour. For each crosslinking reaction, 8~10 μg DNA is used and the protein amount is derived based on a protein to DNA molar ratio of 50:1 in the final crosslinking reaction.

2. Remove TCEP from the DNA by changing to buffer A using the Bio-spin column.

3. Add DTDP to the DNA sample to a final concentration of 1 mM. Incubate at room temperature for one hour.

4. Remove DTDP by changing buffer to buffer C using a PCR purification spin column.

5. Remove TCEP from the protein sample by changing buffer to buffer C. Pass the sample through the Bio-spin columns twice.

6. Mix the protein and DNA samples immediately following steps 4 and 5. Incubate the reaction overnight at room temperature.

4.7 Microfluidic chamber (Fig. 4)

We use a home-made microfluidic chamber in our single-molecule experiments (41). The chamber is formed by sandwiching two microscopic coverslips with nescofilms cut into specific shapes to form three channels: the top and bottom channels for bead injection and the central channel for optical trapping and single-molecule manipulation (Fig. 4D). The top and bottom channels are connected to the central channel through dispenser glass tubing (Fig. 4C). The chamber is affixed to a customized chamber frame (Fig. 4B), connected to plastic tubing (Fig. 4A), and installed on a motorized stage that can move in three axes and positioned between two objectives in a vertical direction.

4.8 Single protein folding studies using optical tweezers

Here, we demonstrate how to pull the gp41 protein using optical tweezers (36). The biotinylated gp41 protein is crosslinked to a 2,260 bp DNA handle that contains two digoxigenin moieties at the protein-distal end. The following protocols describe acquisition of the force-extension curves (FECs) of the gp41 protein and the time-dependent trajectories at constant trap separation.

Measure the force-extension curves

1. Thoroughly wash the three channels in the microfluidic chamber and the connection PE tubing with 3~4 ml PBS using syringes.

2. Bind crosslinked protein-DNA to DIG beads. Mix an aliquot of the crosslinked protein-DNA mixture containing 10–100 ng DNA with 20 μL DIG beads and incubate at room temperature for 15 min. Dilute the beads into 1 mL PBS buffer and transfer the beads to a 1 mL syringe.

3. Dilute 2 μL of streptavidin coated beads into 1 ml PBS. Transfer the beads to a 1 mL syringe.

4. Prepare 3 mL PBS containing the oxygen scavenging system and transfer the PBS to a 10 mL syringe. The oxygen scavenging system consumes free oxygen from the solution by enzymatically catalyzing the oxidation of glucose. The reaction results in a decrease in pH over time. Therefore, the oxygen scavenging solution must be replaced every two to three hours.

5. Connect the syringes to the three channels in the microfluidic chamber through the washed PE tubing and minimize the flow in all three channels.

6. Catch beads. Slowly inject the two types of beads to the top and bottom channels until the beads diffuse from the tips of the dispenser tubes into the central channel. Separate the two optical traps to maximum distance. Move the chamber stage to position one trap near the tip of glass tubing connecting to the top channel and catch a single DNA-bound DIG bead. Similarly catch a single streptavidin-coated bead from the bottom channel.

7. Calibrate optical traps. Flow to clean the beads from the central channel and move the two trapped beads upstream of the two bead fountains. Then stop the flow and measure time-dependent displacements of both beads due to their Brownian motion in optical traps at a bandwidth of 80 kHz. Determine the trap stiffness of both traps and the voltage-to-displacement conversion constants by fitting the measured power-spectrum density distributions to the Lorentz distribution. The typical trap stiffness for our experiments is 0.1–0.2 pN/nm. If the trap stiffness falls out of this range, one can adjust the laser intensity entering the objective.

8. Form a protein-DNA tether. Move the two bead close to allow the biotinylated protein to bind streptavidin on the bead surface and then slowly separate the two beads to check if the force between two the beads increases upon their separation. If the force start to increase, a tether must have been formed between the two beads. Otherwise, repeat the above approach-separation cycle until tether formation. Alternatively, test a different pair of beads.

9. Once a tether is formed, adjust the trap separation speed to 10 nm/s and pull the protein to maximum force until the protein is completely unfolded. Measure the corresponding force-extension curve (FEC). The maximum force is generally limited by digoxigenin-antibody binding strength. With two digoxigenin moieties, the protein-DNA tether typically breaks between 30 pN and 60 pN.

10. Pull more single gp41 protein molecules by repeating the steps 6–9 to confirm the measured FECs.

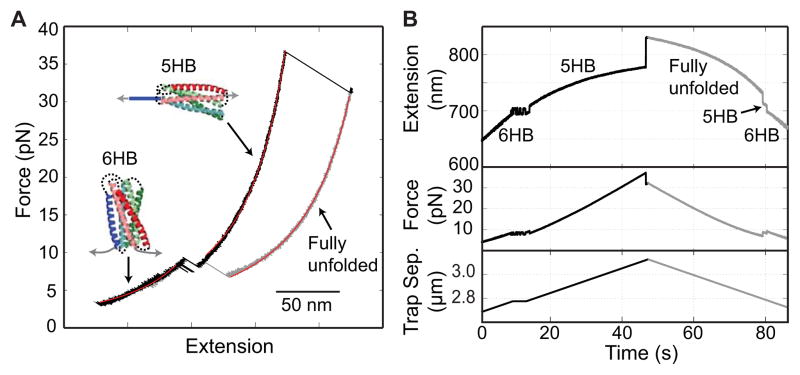
11. Pull to completely unfold the gp41 protein and then relax the gp41 protein to detect protein refolding. Repeat the pulling and relaxation cycle for several rounds to obtain consistent FECs. Finally pull to high force to break the tether. A one-step force drop to zero generally indicates a single protein-DNA tether is studied. A representative FEC is shown in Fig. 5.

12. At the end of the experiment, flush all three channels using sodium azide and then seal the channels in this solution to prevent bacterial growth in the microfluidic chamber.

Fig. 5.

Stage-wise unfolding and refolding a single gp41 SNARE complex (36). (A) Force-extension curves (FECs) obtained by pulling (black) and relaxing (cyan) the gp41 complex. The continuous regions of the FECs are fit with a worm-like chain model (red lines), revealing different gp41 folding states (6HB, 5HB, and the fully unfolded state). (B) Time-dependent extension, force, and trap separation corresponding to the force and extension shown in A. A close-up view of the region marked by the dashed box is shown as an inset.

Measure the time-dependent trajectories at constant trap separation

The time-dependent trajectories at different constant trap separations allow us to pinpoint protein folding energy and kinetics under equilibrium conditions in much greater detail (Fig. 6A). Basically, we pull to unfold the protein in a step-wise manner for each reversible transition. At each trap separation, the protein transition is typically detected for 5 – 500 s, depending on the transition rate. A typical protocol to acquire the trajectories at constant trap separation is listed as follows:

Fig. 6.

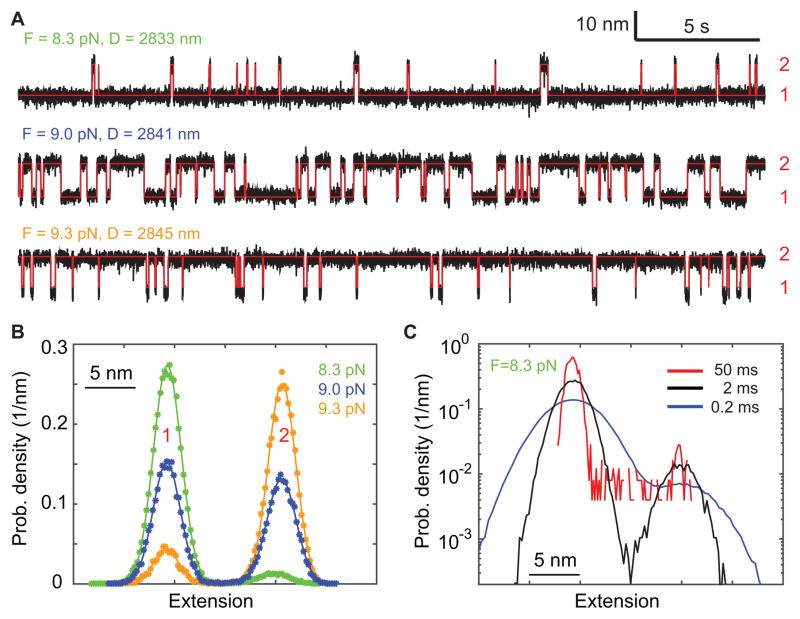
Two-state gp41 hairpin folding and unfolding transition. (A) Extension-time trajectories (black) at three constant mean forces (F) or trap separations (D). The red lines are the idealized extension trajectory derived from hidden-Markov modeling. (B) Probability density distributions of the extensions shown in A. (C) Probability density distributions of the extension at 8.3 pN calculated after mean-filtering the trajectory using three time windows (0.2, 2, and 50 ms).

1. Choose the transition to investigate based on the measured FEC and pull the protein to a force at the lower bound of the force range of the transition.

2. Measure the time-dependent extension, force, and trap separation for a time period such that every state in the transition is visited at least ten times.

3. Increase the trap separation by 2–5 nm.

4. Measure the single-molecule trajectories at incrementally higher forces by repeating steps 2 and 3 until the force reaches the upper bound of the transition’s force range.

5. Measure the FEC of the protein by pulling and relaxing the molecule to confirm its typical FEC.

5. Data analysis

The goal of data analysis is to (1) identify the possible intermediates involved in protein folding, (2) measure conformations, lifetimes, populations, and energies of all the states involved in the folding processes and their associated transition kinetics from the single-molecule measurements in the presence of force, and (3) infer the corresponding parameters in the absence of force. Complementary information on protein folding can be obtained from the force vs. extension curves (FECs) and the time-dependent trajectories at constant trap separation. The former is measured under essentially non-equilibrium conditions, although fast transitions can reach equilibrium when the protein is being slowly pulled. As a result, the protein transition patterns in the measured FECs often depend on the pulling speed. In contrast, the latter is acquired under an equilibrium condition. In addition, protein unfolding and refolding transitions involved in hysteresis seen in the FEC may reach equilibrium under constant trap separation if given sufficient time. In the following, we will describe our methods to analyze results from the two types of experiments.

5.1. Force-extension curves (FECs)

The FECs provide a complete phase diagram of protein folding and unfolding transitions in a large force range. Figure 5A shows an exemplary FEC for the gp41 6-helix bundle. The corresponding time-dependent extension, force, and trap separation are shown in Fig. 5B. At the beginning of the pulling phase (black) in the force range below 7 pN, both force and extension continuously increase with force. This is due to stretching of the elastic DNA handle and any unfolded polypeptide linkers directly attached to the handle or beads (Fig. 1A, green arrows) while the protein remains in the approximately folded 6HB state. The elastic response in such continuous stretches can be quantified using the worm-like chain model (WLC) (53, 54), as shown by the red fitted curves in Fig. 5A. At around 7 pN, the extension starts to flicker as a result of reversible folding/unfolding transitions of the protein between the fully folded state and an intermediate state (Fig. 5B). The unfolding transition increases the tether extension by about 10 nm, suggesting that the intermediate state is a five-helix bundle (5HB) in which the CHR is unfolded. The conformation is confirmed by more quantitative analysis as described below. This extension increase allows the beads to slightly retract towards the trap center, thereby reducing the force by approximately 1 pN. Similarly, refolding is accompanied by extension decrease and force increase. When pulled to higher force beyond 10 pN, the flickering stops at a greater extension, indicating that the gp41 protein is stabilized in the intermediate state. At around 41 pN, the FEC shows an irreversible rip, due to further cooperative unfolding of the protein (Fig. 5A). Pulling the protein to higher force does not reveal any additional unfolding, indicating that the protein is fully unfolded. Then we start to relax the protein to low force to observe its possible refolding (grey). The gp41 protein remains in the fully unfolded state until the force drops to ~ 7 pN, leading to a distinct FEC that is shifted to higher extension compared to the FEC in the pulling phase. Such FEC hysteresis and the irreversibility of the second unfolding transition indicate a large energy barrier for refolding of the fully unfolded gp41 protein construct, at least in the presence force above ~ 7 pN. However, upon further relaxation, the gp41 protein first irreversibly folds into the intermediate state and then reversibly folds to the fully folded state, resulting in a FEC that overlaps with the FEC in the pulling phase in the force range below 6 pN. Therefore, the FECs show different protein folding states, protein folding and unfolding pathways, and approximate stabilities of the different states and their associated transition kinetics.

5.2. Time-dependent trajectories obtained at constant trap separation

We measured gp41 transition in the force region 8 – 10 pN or trap separations 2831 – 2853 nm in a total of seven steps, with approximately 90 s at each step. Figure 6A (black) shows excerpts of the measured time-extension trajectories for three such steps, mean-filtered to 500 Hz bandwidth. Flickering occurs between the 6HB state and the 5HB state, labeled as states 1 and 2, respectively (Fig. 6A, blue). The flickering is overlain with Gaussian noise due to Brownian motion of the beads in the trap. These single-molecule trajectories contain information on both thermodynamics and kinetics of protein folding, which are the major subject of data analysis. In the following, we will use two approaches, the histogram analysis and the hidden-Markov modeling (HMM) to analyze the trajectories. The histogram analysis is easy to understand and to use. It can be utilized to determine the number of states involved in the transition and the extension, population, and force of each state. The HMM involves more sophisticated computer algorithms and is more computationally intensive than the Gaussian fitting. However, HMM can additionally reveal the kinetics of protein transitions with high spatiotemporal resolution.

Histogram analysis

In this method, the histogram or the probability density distribution of the extension or force is calculated based on the corresponding measured trajectory. We will fit the distribution with a sum of multiple Gaussian functions to determine the number of distinct states involved in the protein transition and their associated average extensions, forces, and probabilities. The fitting with Gaussian functions is justified, because the major measurement noise in OT comes from Brownian motion of the beads in harmonic potentials imposed by the optical traps (24). The histogram analysis can be similarly performed on both the extension-time and the force-time trajectories for each trap separation. For simplicity, we use the extension trajectory as an example to demonstrate the histogram analysis:

1. Choose the time region of interest in the whole extension-time trajectory and parse the trajectory into segments corresponding to different trap separations. Mean-filter the trajectories using a proper time window to reduce the noise without blurring the protein transitions.

2. Calculate the probability density distribution of the extension ρ(X). The probability density is calculated as the number of extension data points N_i falling into the i-th bin with an average extension of X_i, i.e., ρ_i = N_i/(N_T dX), where N_T is the total number of data points in all bins and dX the size for each bin. The bin number should be chosen to reveal a smooth distribution with a maximum number of distinct peaks, which typically ranges from 20 to 100. If a peak is not clear, choose a different mean-filtering time window and repeat steps 1–2. In general, an increase in the time window leads to a decrease in the amplitude of fluctuation around each peak, which may distinguish two peaks that are otherwise overlapping in the distribution that is obtained using a smaller time window (Fig. 6C and Fig. 8). In principle, the time window should be at least two-fold smaller than the smallest lifetime of the state involved in the transition. Based on the probability density distribution, one can estimate the number of states N_st as the number of distinct peaks in the distribution.

3. Fit the probability density distribution with a sum of N_st Gaussian functions. Good fitting confirms the number of states identified.

4. Calculate the average extension, fluctuation, and probability of each state from the best-fit parameters.

Fig. 8.

Extension-time trajectories mean-filtered using different time windows (A) and their corresponding probability density distributions (B). The three trajectories are filtered from the same trajectory exhibiting two-state folding and unfolding transition of the SNARE linker domain (13).

Figure 6B shows the extension histograms corresponding to the trajectories shown in Fig. 6A. Two distinct peaks in the histogram distributions (symbols) are accurately fitted with double-Gaussians (solid curves), indicating a two-state transition. Prominence of the peaks strongly depends on the time window used in data filtering and becomes optimal with a time window of 2 ms (Fig. 6C, crosses). The histogram analysis reveals the state positions, populations, forces, and position difference between the two states (Fig. 7A–C, red and cyan).

Fig. 7.

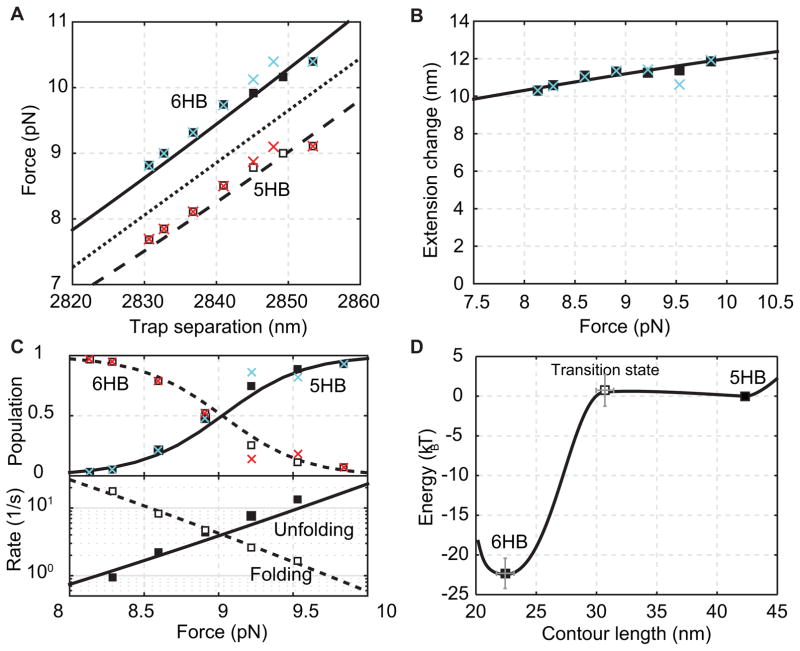
Comparison of properties of the gp41 hairpin transition derived from the histogram analysis (crosses), the HMM analysis (squares) and best model fitting (dashed and solid curves). (A) Average forces of the folded state (solid square or cyan cross) and the unfolded state (hollow square or red cross) as a function of trap separation. The mean force is shown as the dotted line. (B) Extension difference between the folded and unfolded states as a function of the mean force. (C) State populations (top) and transition rates (bottom) as a function of the mean force. (D) Simplified energy landscape of gp41 hairpin folding at zero force determined by the model fitting in A–C.

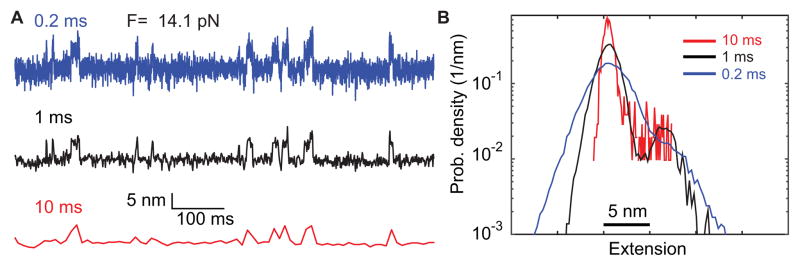
The gp41 trajectories have a high signal-to-noise ratio, because the state transition is relatively slow and involves a large extension change. Figure 8A shows a trajectory with a low signal-to-noise ratio that is mean-filtered with a 0.2 ms time window (blue). The extension trajectory barely exhibits folding and unfolding transition of the SNARE linker domain at a constant mean force of 14.1 pN, as is shown by a unimodal extension histogram distribution (Fig. 8B, blue). However, when the same trajectory is mean-filtered using 1 ms time window (black), a distinct two-state transition is seen from both the extension trajectory and the corresponding probability density distribution. In contrast, the two-state transition becomes indiscernible when further smoothing the trajectory using a 10 ms time window (red). This comparison demonstrates that proper filtering of the time-dependent trajectory is important to reliably extract information from the trajectories and histogram distributions.

Hidden-Markov modeling (HMM)

HMM models the state transitions underlying the observed trajectory using a Markov model and the associated measurement noise using a Gaussian model (28, 55, 56). HMM assumes that the noise is uncorrelated. This assumption holds true as long as HMM is performed on the extension trajectory filtered to a bandwidth below the corner frequency of bead Brownian motion. We typically mean-filtered the time series to 5 kHz or 1 kHz and then carried out HMM (27). Given a hidden-Markov model, the likelihood to observe a single-molecule trajectory can be computed using the forward-backward algorithm. In addition, the corresponding state transitions (or a Markov chain) can be calculated by the Viterbi algorithm. More importantly, HMM can optimize the model parameters by maximizing the likelihood of observing the trajectory based on the model, which is efficiently implemented by Baum’s algorithm. The algorithm iteratively optimizes model parameters. The hidden-Markov model used for the extension-time trajectory includes the number of states (N_st), their transition probabilities (P_ij from sates i to j, i, j =1, …, N_st) during each time step (dt), their average extensions, and the state fluctuations. These optimized model parameters are used to calculate state properties. In particular, the transition rate between states i and j is calculated as k_ij = P_ij/dt and the state probability p_i, i =1, …, N_st is computed as the eigenvector p of the transpose of the transition probability matrix P. Finally, the lifetime of state i is calculated as ${\tau }_i=1/{\displaystyle \sum _{j\ne i}}{k}_{ij}$. The typical protocol to perform HMM is listed below.

Baum’s algorithm requires inputs of initial tentative model parameters. Although the final optimized parameters are independent of the initial parameters, the inputs affect the computation time required for the iterative algorithm to reach convergence, especially for the trajectories with a low signal-to-noise ratio. We typically use outputs from the histogram analysis as the input for the HMM analysis.

1. For each segment of the trajectory corresponding to a constant trap separation, record the trap separation, the beginning and ending time points, and the state extensions determined from the histogram analysis. List all these parameters in a text file, with one row for each trap separation, to be read by the MATLAB program that carries out the HMM analysis.

2. Set the initial model parameters for HMM analysis. We choose as initial state positions the values loaded from the text file prepared in step 1. Set other parameters as constants that are independent of states and trap separations. In particular, the state fluctuation is chosen as 3 nm and the transition probability matrix is set to values corresponding to a lifetime of 10 ms for each state.

3. Run the MATLAB program to compute the optimized model parameters that maximize the likelihood.

4. Calculate the idealized sequence of state transitions using the optimized model parameters. Verify the HMM fitting by comparing the idealized and measured trajectories.

5. Calculate the average state forces based on the idealized state transitions for the extension trajectory.

6. Plot the state extensions, forces, populations, lifetimes, and transition rates as a function of trap separation.

Using a two-state hidden-Markov model, we fitted the gp41 extension trajectory at each trap separation (Fig. 6A, red) and determined average populations, extensions, forces, lifetimes, and fluctuations of all states and their associated transition rates (Fig. 7A–C). We found that in the narrow force range of the reversible gp41 transition, the average forces of both folded and unfolded states increased approximately linearly with trap separation (Fig. 7A). Thus, we used the mean of the state forces to represent the force applied to the molecule (Fig. 7A, dotted), which is used throughout the text if not otherwise specified. Similarly, the extension change upon the state transition slightly and linearly increases with the force, due to stretching of the unfolded polypeptide (Fig. 7B). The state populations show a sigmoidal shape, consistent with a two-state transition (Fig. 7C). The two states equilibrates at a force of 9.0 ± 0.1 pN, characterized by equal folding/unfolding rates and populations. Finally, the state forces, extensions, and populations obtained from the HMM analysis match the corresponding calculations from the histogram analysis, demonstrating the consistency between both methods of data analysis.

Model fitting to derive the conformations and energies of protein folding states

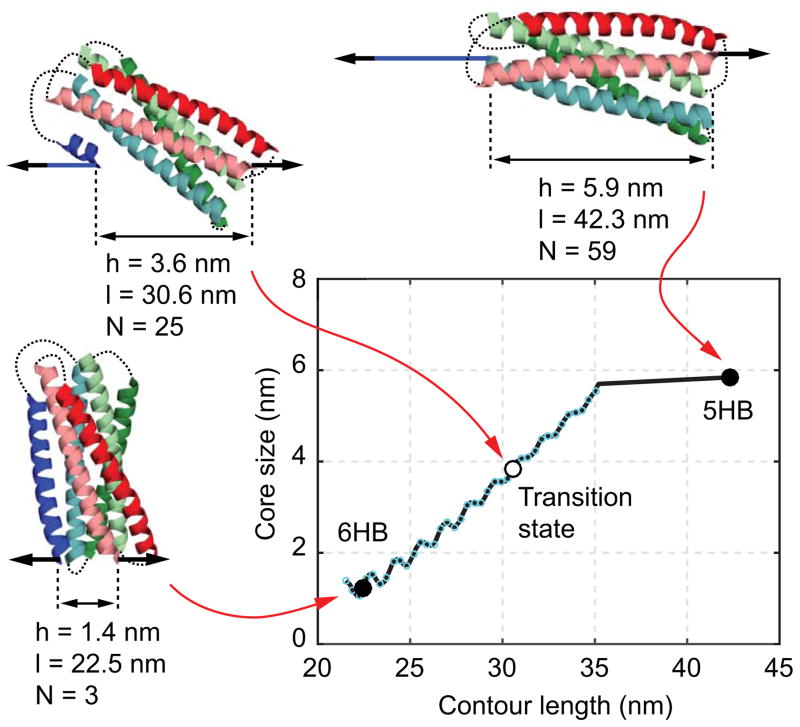
We fit the HMM-derived observables with a non-linear model to derive the conformations and energies of all states involved in the transition in the absence of force (57). The model assumes an unfolding pathway, which we inferred from the crystal structure of the protein in its native state. Protein conformations along the pathway are parameterized using the contour length of the unfolded and stretchable polypeptide l (Fig. 9). In the inferred gp41 unfolding pathway, amino acids in the CHR (blue) are successively peeled, from its C-terminus to N-terminus, off the remaining five-helix bundle (5HB). Folding of gp41 exactly reverses this process. Each unfolded amino acid contributes 0.365 nm to the contour length. For instance, the folded state of the gp41 shown in Fig. 1A has a total of 59 unstructured and stretched amino acids stemming from the polypeptide linkers indicated by the green arrows. Accordingly, the contour length of the folded state is 59×0.365 nm = 21.535 nm. Fully unfolding the blue CHR, including the linker indicated by the red arrow, contributes an additional 57 amino acids to the contour length (37 from the helix and 20 from the linker). The resulting contour length of this state is (59+57)×0.365 nm = 42.340 nm. Importantly, the remaining structured portion of the protein is assumed to remain in its native conformation. As a result, the contour length unambiguously specifies conformations along the inferred folding/unfolding pathway.

Fig. 9.

The size of the folded gp41 portion as a function of the contour length of the unfolded polypeptide calculated from the crystal structure of the gp41 six-helix bundle (57). The gp41 conformations and their associated core sizes (h), contour length positions (l), and numbers of amino acids unfolded (N) are shown as insets.

The full energy landscapes of protein folding can be obtained from high-resolution measurements of protein folding trajectories from optical tweezers (50, 58), which requires sophisticated deconvolution method. Here we characterize protein folding/unfolding transition in terms of the simplified energy landscape (l_i,V_i), where l_i is the contour length of the unfolded peptide in the i-th, stable state or transition state, and V_i is the associated free energy at zero force. Model fitting for gp41 involves two stable states, i.e., the folded 6HB state and the unfolded 5HB state, and one transition state. For a given set of parameters (l_i,V_i) and trap separation D the model computes the tether extensions X_i, state forces F_i, and the total energies G_i of the protein-DNA tether and trapped beads. The energies G_i directly yield state populations and transition rates via the Boltzmann distribution and the Kramers’ equation, respectively. Consequently, we can determine (l_i,V_i) by simultaneously fitting the model-based calculations to all the experimental measurements obtained at different trap separations (Fig. 10). Note that for the unfolded gp41 5HB state, the contour length of the unfolded polypeptide is known and its free energy is chosen as zero. Thus, the parameters (l_i,V _i) associated with the folded state and the transition state, but not the unfolded state, are chosen as fitting parameters.

Fig. 10.

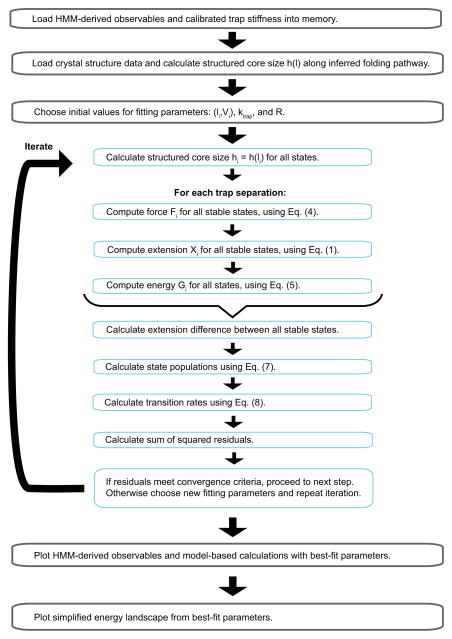
Flowchart to optimize model parameters by fitting model calculations to the experimental measurements.

Specifically, the tether extension in the i-th state is expressed as

$$X_i=x^{(m)}(F_i,l_i)+H(F_i,l_i)+x^{(\mathit{DNA})}\left(F_i\right),$$ (1)

where x^(m) and H are the extensions of the unfolded and stretched polypeptide and the folded protein portion, respectively, and x^(DNA) is the extension of the DNA handle. The extensions x^(DNA) and x^(m) at state force F_i are implicitly given by the Marko-Siggia formula for a semi-flexible worm-like chain (WLC) (54):

$$F_i=\frac{k_{B}T}{P}\left[\frac{1}{4{\left(1-\frac{x}{L}\right)}^2}+\frac{x}{L}-\frac{1}{4}\right],$$ (2)

where P is the persistence length and L the contour length of the polymer. For DNA, P= 40 nm and L = 0.34 × N_bp nm, where N_bp is the number of base pairs in the DNA handle and for polypeptide, P= 0.6 nm and L = l_i. The extension of the folded protein portion H is calculated based on a freely jointed chain model, i.e.,

$$H_i=-\frac{k_{B}T}{F_i}+h_i\mathit{coth}\left(\frac{F_i{h}_i}{k_{B}T}\right),$$ (3)

where h_i is the size of the folded protein portion along the pulling direction, which is measured from the crystal structure as a function of the contour length l (Fig. 9). Furthermore, the tether extension X_i is related to the trap separation D by

$$D=X_i+\frac{F_i}{k_{\mathit{traps}}}+R,$$ (4)

where F_i/k_traps is the total bead displacement with k_traps = k₁k₂/(k₁ + k₂) the effective trap stiffness of the two traps, and R is the sum of the bead radii (Fig. 1A). Substituting Eq. (1)–(3) into Eq. (4) and solving for F_i yields the state force.

The total energy of the protein, the DNA handle, and trapped beads is expressed as

$$G_i=G^{(m)}(F_i,l_i)+V_i+G^{(\mathit{DNA})}(F_i)+\frac{F_i^2}{2k_{\mathit{traps}}},$$ (5)

where G^(m), G^(DNA), and F_i/k_traps are the energies of the unfolded polypeptide, the DNA handle, and the beads in optical traps, respectively. G^(m), G^(DNA) result from the entropy change of the worm-like chain due to stretching and are calculated as

$$G_i^{(mor\mathit{DNA})}=\frac{k_{B}T}{P}\frac{L}{4\left(1-\frac{x}{L}\right)}\left[3{\left(\frac{x}{L}\right)}^2-2{\left(\frac{x}{L}\right)}^3\right].$$ (6)

The state populations P_i are related to the system energies G_i of stable states by the Boltzmann distribution, i.e.,

$$P_i=\frac{e^{-\frac{G_i}{k_{B}T}}}{{\sum }_{j=1}^N{e}^{-\frac{G_j}{k_{B}T}}},$$ (7)

Where N is the total number of stable states involved in the protein transition. In addition, the transition rate k_ij from state i to state j is calculated using the Kramers’ equation

$$k_{ij}=k_m{e}^{-\frac{G_{ij}-G_i}{k_{B}T}},$$ (8)

where G_ij is the free energy of the transition state between stable states i and j, and the pre-factor k_m is the diffusion-limited rate constant in the absence of any energy barrier. No consistent pre-factor has been obtained, with a wide range of values reported in literature (10⁵ – 10⁹ s⁻¹), depending on the measurement method and the protein investigated (32, 59, 60). For coiled-coil proteins such as gp41 and SNARE complex, we use k_m =10⁶ s⁻¹, consistent with the maximum folding speed observed for short helical proteins.

Last, we use the non-linear least-squares method to fit the model-based calculations at all trap separations to the corresponding experimental measurements. The target function is the sum of the squared residuals of state forces, populations, logarithms of the transition rates, and extension differences between folded and unfolded states. The fitting yields the best-fit parameters for the simplified energy landscape at zero force. The flowchart for the model fitting is shown in Fig. 10.

The fitting results obtained for the 2-state transition of gp41 are shown in Fig. 7A–C as curves. The experimental data are well fit by the model, corroborating our model. Figure 7D exhibits the optimized energy landscape parameters (l_i,V_i). Thus, the folding energy of a single gp41 hairpin in the gp41 complex 22 k_BT. The best-fit contour lengths l_i reveal an approximately 6HB conformation in the folded state, with 3 amino acids unfolded at the C-terminal end. The frayed end may be due to marginal instability of the C-terminal end under tension or experimental error. In addition, the folding proceeds over a small energy barrier of 1 k_BT, whose position lies close to the 6HB state (Fig. 7D).

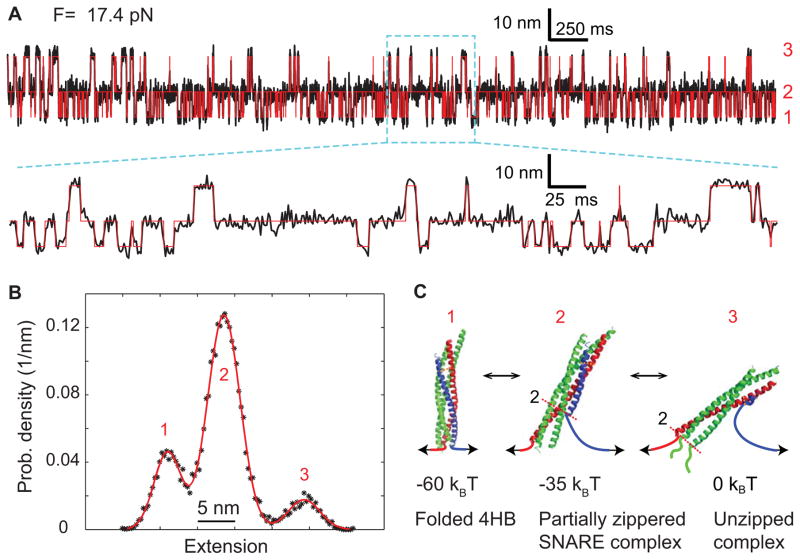
Similarly, we analyze the extension-time trajectory of a single SNARE complex pulled to a force of 17.4 pN (13). Smoothed to 1 kHz, the trajectory shows a three-state folding/unfolding transition of the SNARE four-helix bundle (Fig. 11A), as is demonstrated by the three distinct peaks in the corresponding probability density distribution that can be fit by a sum of three Gaussian functions (Fig. 11B). Accordingly, the extension can be well simulated by a three-state hidden-Markov model (Fig. 11A, red). Detailed model fitting reveals that the three states are the folded 4HB state (state 1), the partially zippered SNARE complex (state 2), and the unzipped state (state 3), as well as their associated folding energies (Fig. 11C). These results showcase the applicability of the single-molecule manipulation approach to more complex protein folding transitions with multiple intermediates.

Fig. 11.

Three-state folding and unfolded transitions of the SNARE complex (13). (A) Extension-time trajectory at a constant mean force of 17.4 pN. The red line shows the idealized extension trajectories derived from a three-state hidden Markov model. A close-up view of the region marked by a cyan box is shown. Data were mean-filtered to 1 kHz and plotted. (B) Probability density distribution of the extension shown in A. (C) Derived conformations of the three SNARE folding states and their energies.

6. Notes

1. In the protein purification part of section 4.3, the imidazole concentration in the lysis buffer can be adjusted to a lower concentration (e.g., 1 mM) if the target protein binds poorly to the Ni-NTA column or a higher concentration (e.g., 20 mM) if too many proteins nonspecifically bind the column.

2. In step 10 (elution) of protein purification in section 4.3, treating the beads with the elution buffer often fails to completely elute the protein. To improve the protein yield, one may elute the protein from the beads twice (600 μL for each elution) or increase the imidazole concentration up to 500 mM.

3. In the in vitro biotinylation step in section 4.4, many commonly used reagents such as glycerol (5%) and NaCl (100 mM) inhibit the BirA activity. Thus, the concentration of these reagents should be minimized in the biotinylation reaction. In addition, a high substrate concentration leads to higher yield of biotinylation. Finally, the biotinylation reaction may be carried out at a higher temperature, for example 30°C, for higher rate and yield of protein biotinylation.

4. To prepare greater amount of the DNA handle (section 4.5), we usually scale up the PCR mixture to 1 mL and then aliquot the mixture to 50 μL per PCR tube.