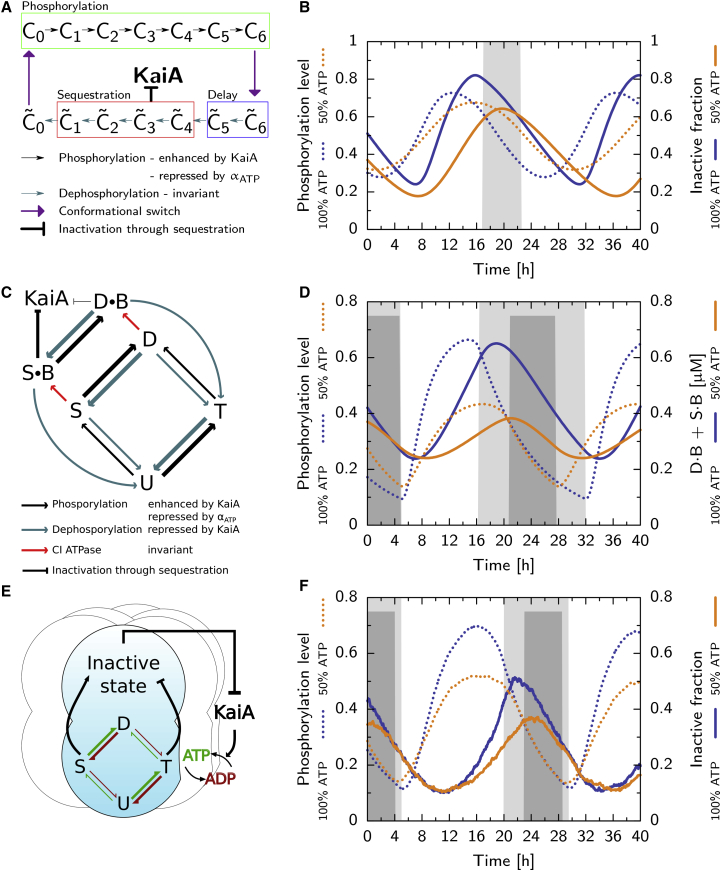
Figure 1.

The different models of the Kai system employ different mechanisms of period stabilization. Shown are: (A and B) the Van Zon model; (C and D) the Rust model ((C) after (27)); and (E and F) the Paijmans model. Phosphorylation level (dotted lines, B, D, and F) and fraction of KaiC in inactive state (solid lines, B and F) or in S$\cdot$ B + D$\cdot$ B (D, solid lines) at α_ATP = 100% and 50% (in (B), (D), and (F), see key next to the vertical axis label). Shaded regions indicate the phase where all KaiA is sequestered, at α_ATP = 100% (gray) and 50% (dark gray). (A) Given here is the Van Zon model: hexamers phosphorylate in the active phase (box, “Phosphorylation”), with a rate that depends on α_ATP and the amount of free KaiA, switch to the inactive state where they dephosphorylate and, after a delay (box, “Delay”), sequester KaiA (box, “Sequestration”). (B) Both the phosphorylation level and the fraction of inactive hexamers rise slower at α_ATP = 50%, but due to the delay between phosphorylation and KaiA sequestration, the dephosphorylation phase starts at a lower maximum of the inactive fraction, which shortens the time window where all KaiA is sequestered. (C) Given here is the Rust model: the monomer is predominantly phosphorylated in the order U, T, D, and S. Phosphorylation depends on the ATP fraction and KaiA; dephosphorylation only on KaiA (see key in (C)). To emphasize that phosphorylation of the threonine site is much faster than for the serine site, the arrows indicating (de)phosphorylation of the threonine site are thicker. The delay is set by the slow KaiB binding step (see key in (C)), and mutual inhibition between KaiA and the sequestration state S$\cdot$B. (D) Because at α_ATP = 50% the rate from S to D is smaller, the ensemble starts the dephosphorylation phase at a lower concentration of KaiB-bound KaiC. This shortens the dephosphorylation phase, which compensates for slower phosphorylation. (E) Given here is the Paijmans model: in each hexamer, monomers go through the ordered phosphorylation cycle, where T stabilizes the active state, and S the inactive state. Phosphorylation can only occur with ATP and dephosphorylation only with ADP (see key in (E)) in the CII binding pocket. (F) The inactive fraction (solid lines) increases more slowly at α_ATP = 50%, but reaches a lower maximum, leading to a shorter dephosphorylation phase. However, the effect on the duration of the KaiA sequestration phase is not as strong as in the Rust model. Because in the Paijmans model the switch to the inactive state depends not on the absolute number of serine and threonine phosphorylated residues, but rather on their difference, the decrease in the phosphorylation level (dotted lines) has a smaller impact on the inactive fraction (solid lines), as compared to the impact on the S$\cdot$B + D$\cdot$B fraction in the Rust model (D). Our simulations of the Van Zon and Rust models employ ordinary differential equations, but the Paijmans model can only be described by stochastic simulations (32). Hence the curves in F show a small amount of noise that is absent in (B) and (D). To see this figure in color, go online.