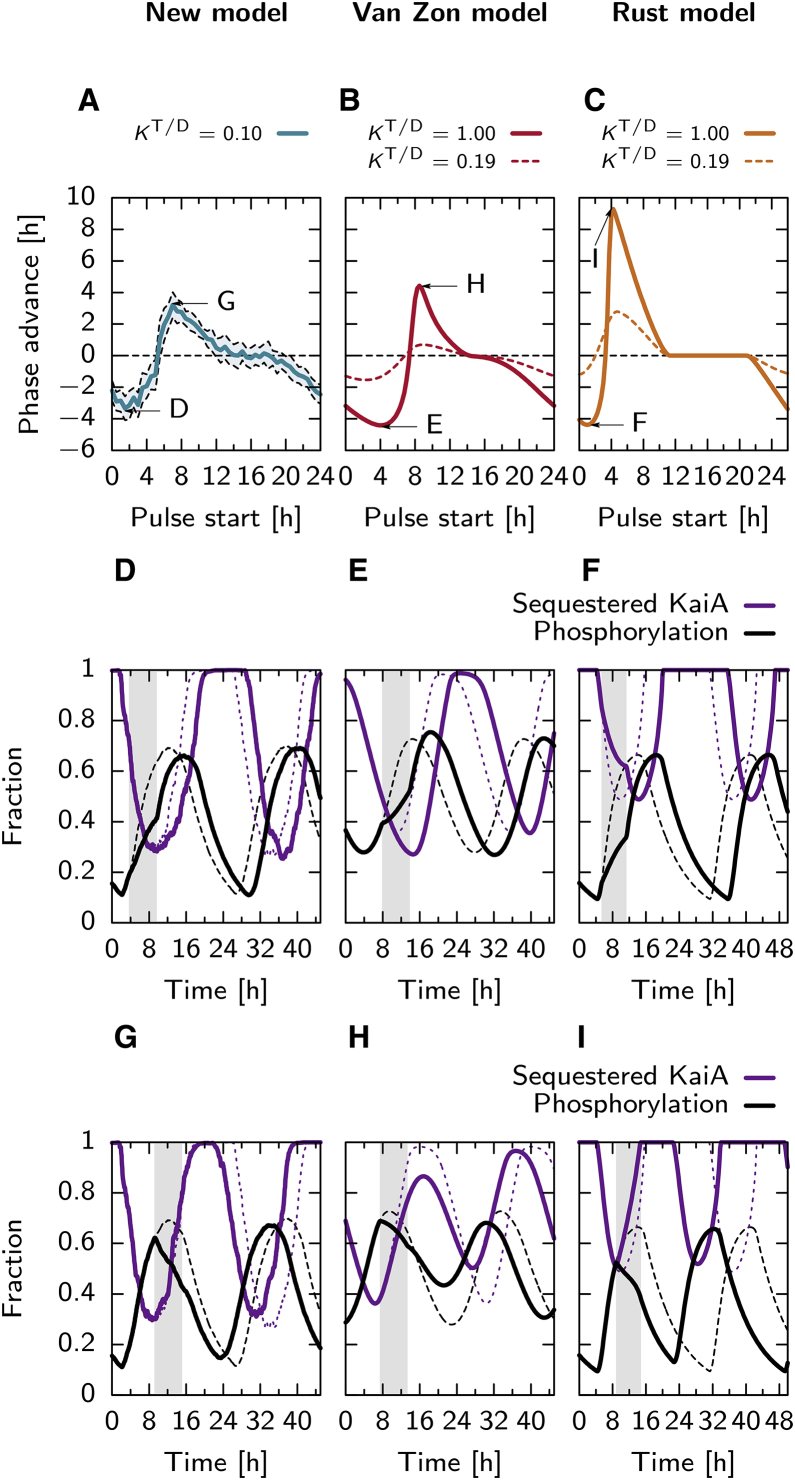
Figure 3.

Shown here is the sensitivity of the phase of the phosphorylation level, in the Paijmans model (left column), Van Zon model (middle column), and the Rust model (right column), to a 6 h pulse lowering of the ATP fraction to 40%. (A–C) Given here is the phase advance in hours, due to the pulse, starting at the time indicated on the x axis, measured from the minimum in the phosphorylation level. The shaded region in (A) shows the standard deviation of 10 independent runs of the Paijmans model, which, contrary to the other two models, is stochastic. For the Van Zon and Rust models, we show phase response curves for a scenario with an equal relative affinity for ATP and ADP, K_ATP/ADP = 1.0 (solid line), and a version with a lower affinity for ADP, K_ATP/ADP = 0.19 (dashed line). Arrows indicate extrema in the phase response curves, for which we show the corresponding time traces in the panels with the adjacent label. (D–F) Here we show the effect of a pulse (shaded region) when the phase delay is the largest, on the phosphorylation level and the fraction sequestered KaiA (see keys in (F) and (I)). Dashed lines show the development in the case no pulse is given. (G–I) Here we show the effect of the pulse when the phase advance is the largest. Results for the Paijmans model were obtained using kinetic Monte Carlo, and ordinary differential equations were used for the Van Zon and Rust models. To see this figure in color, go online.