Designing therapeutic cancer vaccine trials with delayed treatment effect

Abstract

Arming the immune system against cancer has emerged as a powerful tool in oncology during recent years. Instead of poisoning a tumor or destroying it with radiation, therapeutic cancer vaccine, a type of cancer immunotherapy, unleashes the immune system to combat cancer. This indirect mechanism-of-action of vaccines poses the possibility of a delayed onset of clinical effect, which results in a delayed separation of survival curves between the experimental and control groups in therapeutic cancer vaccine trials with time-to-event endpoints. This violates the proportional hazard assumption. As a result, the conventional study design based on the regular log-rank test ignoring the delayed effect would lead to a loss of power. In this paper, we propose two innovative approaches for sample size and power calculation using the piecewise weighted log-rank test to properly and efficiently incorporate the delayed effect into the study design. Both theoretical derivations and empirical studies demonstrate that the proposed methods, accounting for the delayed effect, can reduce sample size dramatically while achieving the target power relative to a standard practice.

1. Introduction

In a relatively short period of time, therapeutic cancer vaccine has entered the mainstream of cancer therapy. Instead of poisoning a tumor or destroying it with radiation, the underlying basis of therapeutic cancer vaccine is to unleash the immune system to fight cancer [1]. The idea of manipulating anti-cancer immune response is not new, but only recently have several scientific studies demonstrate what a game-changer therapeutic cancer vaccine can be [2–4]. Consequently, cancer vaccines have set off a frenzy in the pharmaceutical industry and many drug companies are racing to conduct such trials.

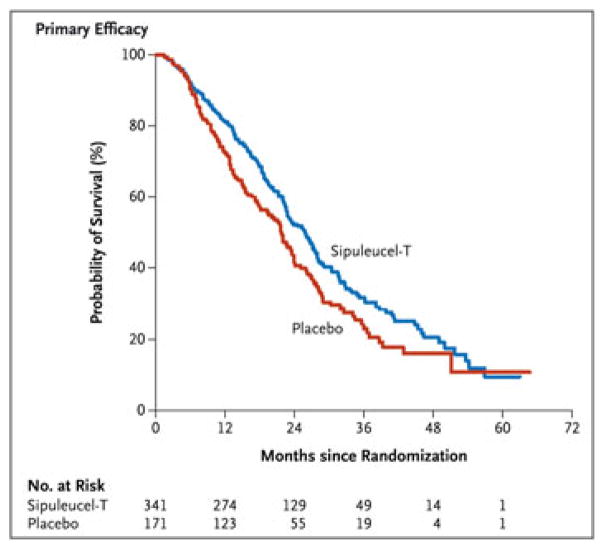
One typical feature of therapeutic cancer vaccine trial is the delayed onset of clinical effect. This delay is largely caused by the indirect mechanism-of-action of the vaccine, which requires the time to mount an effective immune response and the time for that response to be translated into an observable clinical response. Thus, in such trials with a time-to-event endpoint, the delayed effect results in a pattern of delayed separation of survival curves between experimental and control arms [1, 5]. For example, the study of Sipuleucel-T, the first therapeutic cancer vaccine approved by the Food and Drug Administration, shows a delayed separation of survival curves by 6 months [6] in a Kaplan–Meier plot (Figure 1). This implies that the proportional hazard assumption no longer holds in cancer vaccine trials, and the standard sample size and power calculation methods based on conventional log-rank test would generally lead to a loss of power [7–12]. Hence, designing innovative clinical trials to incorporate this unique feature of cancer vaccine trials becomes essential.

Figure 1.

Kaplan–Meier estimates of overall survival in the pivotal study underlying the approval of Sipuleucel-T.

The standard practice to account for delayed effect is either ignoring the delay or increasing the sample size. However, each approach has its own limitations. Specifically, ignoring the delay will result in a loss of power or an increased chance of falsely claiming futility at early trial stage. Increasing the sample size, on the other hand, would increase cost, prolong the study duration and may still violate the proportional hazard assumptions as no valid theory has been proposed with regard to how much an increase is appropriate.

Therefore, the question of interests becomes how to properly incorporate the delayed effect into the design of therapeutic cancer vaccine trials.

There is much literature dealing with clinical trials with delayed treatment effect based on various classes of weighted log-rank tests [10, 13–19]. Self et al. [13] discusses a sample size and power calculation method using weighted log-rank test with corresponding linearly increase weights for the design of the Women’s Health Initiative, as it was anticipated that the effect of dietary changes would be delayed. However, the method ignores time and may not be appropriate in the therapeutic setting of cancer vaccines. Lakatos [10] considers the Tarone–Ware class of weights in designing complex clinical trials with the presence of lag time. This method can up-weight the later events after the delayed onset but assumes that the subsequent analysis would be by a standard method without accounting for the delay. Zucker and Lakatos [14] discuss two weighted log-rank types of statistics designed to have good efficiency over a wide range of lag time functions, which can be applied in situations where a delayed effect is expected but cannot be specified precisely in advance. However, the authors do not derive an analytic approach for sample size and power calculation based on the proposed test statistics. In recent years, Fine [16] and Hasegawa [18] present similar methods for calculating sample sizes with the Fleming–Harrington’s G^ρ,λ class of weights [20, 21]. Although this class of weights, if properly specified, is more general, it is not specifically designed to address the standard delayed effect problem in which the treatment has no detectable effect prior to the delayed onset. In particular, despite that this method can weight the later events after the delayed onset more heavily, it also takes into account the early events before the delayed onset; for this reason, it is not an optimal method to maximize power under the delayed effect scenario. In addition, the problem of choosing an appropriate and robust Fleming–Harrington’s G^{ρ, λ} class of weights in practice has not been systematically investigated, and the complicated weight structure hinders in developing a simple analytic approach for the sample size and power calculation. Therefore, it is of particular interests and increasing demands to develop an efficient and powerful approach to design studies with delayed effect.

In this paper, we first propose a new weighted log-rank test, the piecewise weighted log-rank test. In contrast to the existing large family of weighted log-rank tests, the proposed test is shown to be the most powerful weighted log-rank test by optimally allocating more (or full) weights to a subset of events which contribute more (or fully) to the detection of treatment effect, under the pre-specified delayed effect scenario. Next, we develop new approaches for the sample size and power calculation based on the proposed piecewise weighted log-rank test:

1. Analytic power calculation method based on piecewise weighted log-rank test (APPLE),

2. Simulation-based empirical power calculation method based on piecewise weighted log-rank test (SEPPLE).

APPLE is a simple analytic approach with close-form formula, which is easy to perform in practice under the pre-specified delayed effect scenarios, whereas SEPPLE is a Monte Carlo simulation-based algorithm. The purpose of SEPPLE is to verify the analytic approximation of APPLE as well as compute the empirical power. In addition, SEPPLE can provide a more flexible framework in the power calculation by incorporating more complex enrollment process or event time distribution than APPLE.

In general, the proposed piecewise weighted log-rank test and corresponding sample size and power calculation algorithms have two advantages. First, they maximize the asymptotic study power provided the delayed pattern being correctly specified. In case of mis-specified delayed patterns, the proposed approaches can still achieve substantial gain in power compared with the conventional approaches ignoring the delayed effects, among the scenarios considered. Second, they provide an easy, elegant, and intuitive solution to address the delayed effect challenge. It is obvious that the proposed methods rely critically on the proper pre-specification of the delayed pattern. In practice, the investigators can obtain good estimates of the true delayed pattern using the biological or medical judgments on the mechanism-of-action of the therapeutic agent, prior knowledge gained from lab studies and animal models, and preliminary data from the early phase clinical trials. Both theoretical derivations and extensive empirical studies demonstrate that the proposed methods can reduce sample size dramatically while achieving the target power relative to the standard practice when the delayed effect is present.

The rest of this paper is organized as follows. The piecewise weighted log-rank test is presented in Section 2. The APPLE approach is introduced in Section 3, and the SEPPLE approach outlined in Section 4. Section 5 gives results of simulation studies evaluating the characteristics of the APPLE and SEPPLE methods as opposed to the standard practice based on a conventional log-rank test by ignoring the delayed effect and to the EAST procedure (version 6.0) [22] by considering the delayed effect. The article concludes with a discussion in Section 7.

2. Piecewise weighted log-rank test

Consider a study to compare survival curves with n subjects randomly allocated to experimental and control groups labeled as E and C, with probability P_E and P_C (P_E + P_C = 1), respectively. Let D, with size n_D, be the set of indices of patients who experienced the event of interest. At each distinct event time t_j, j = 1,…, n_D, with no ties, denote by n_i(t_j) (i = {E, C}) the number of subjects who are at risk up to time t_j in group i and by X_j ∈ {0, 1} the indicator whether the j^th event is from the experimental group. Then, p(t_j) = n_E(t_j)/{n_E(t_j) + n_C(t_j)} is the proportion of subjects at risk at time t_j in the experimental group.

To test the hypothesis H₀ : h_E(t) = h_C(t), where h_E(t) and h_C(t) are the underlying hazard functions for the experimental and control groups, a conventional weighted log-rank test statistic S is constructed as follows:

$$S=\sum _{j\in D}{b}_j\{X_j-p(t_j)\}/{\left[\sum _{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}\right]}^{1/2}$$ (1)

where b_j is the pre-determined weight at the event time t_j. When each b_j = 1, S is the most commonly used regular log-rank test statistic. The regular log-rank test is asymptotically fully efficient under the proportional hazard alternative. When the delayed effect exists, the hazard ratio λ(t) = h_C(t)/h_E(t) varies once the treatment effect is manifested, and the proportional hazard assumption is violated. As a result, the regular log-rank test is no longer the most efficient test asymptotically as shown in Theorem 2.1.

Theorem 2.1

Under condition log{h_C(t)/h_E(t)} = O(n^−1/2) as n → ∞, the asymptotic power of conventional weighted log-rank test is maximized when weights at event times are proportional to the log of the hazard ratios at those times.

Proof

See Appendix.

With the general aim of optimizing the study power with respect to the pre-defined weights, a piecewise weighted log-rank test is therefore proposed when a delayed effect exists. Let t^* denote the hazard ratio changing point, which also measures the treatment effect delayed duration since randomization. Under the general delayed effect scenario,

$$H_1:\lambda (t)=h_C(t)/h_E(t)=\{\begin{array}{ll}{\lambda }_1,\hfill & t\le t^{\ast }\hfill \\ {\lambda }_2,\hfill & t>t^{\ast }\hfill \end{array}$$

with λ₂ > λ₁ ≥ 1, the proposed test statistic of the piecewise weighted log-rank test takes the following form:

$$S_w=\frac{{\sum }_{j\in D_1}{w}_1\{X_j-p(t_j)\}+{\sum }_{j\in D_2}{w}_2\{X_j-p(t_j)\}}{{\left[{\sum }_{j\in D_1}{w}_1^{2}p(t_j)\{p(t_j)\}+{\sum }_{j\in D_2}{w}_2^{2}p(t_j)\{1-p(t_j)\}\right]}^{1/2}},$$ (2)

where we assign weights w₁ = log(λ₁)/{log(λ₁)+log(λ₂)}, w₂ = log(λ₂)/{log(λ₁)+log(λ₂)} and denote by D₁,D₂ the sets of indices of patients who died before and after t^*, respectively. According to Theorem 2.1, S_w can maximize the power of the study for a given sample size under the general delayed effect scenario. We can easily see that the piecewise weighted log-rank test statistic (S_w) is a special form of the conventional weighted log-rank test statistic (S) by assigning piecewise constant weights to the earlier and later events differentiated at the changing time t^*. Specifically, b_j = w₁ if t_j ≤ t^*, b_j = w₂ if t_j > t^* and the weights b_j ∝ log λ(t_j).

In practice, the standard delayed effect scenario often arises where the treatment has no detectable effect during the period [0, t^*], and becomes fully effective afterwards; that is, λ₂ > λ₁ = 1 as demonstrated in the Sipuleucel-T study. In this case, the optimal weights are w₁ = 0, w₂ = 1, and the test statistic becomes

$$S_{ws}=\frac{{\sum }_{j\in D_2}\{X_j-p(t_j)\}}{{\left[{\sum }_{j\in D_2}p(t_j)\{1-p(t_j)\}\right]}^{1/2}}.$$

As shown in the Appendix, with equal allocation ratio so the censoring distributions are the same, S_ws can maximize the study power at

$${\mathit{Pow}}^{\ast }=\mathrm{\Phi }\left\{\frac{1}{2}log({\lambda }_2)\sqrt{d_2}-Z_{1-\frac{\alpha }{2}}\right\},$$ (3)

where we consider an one-sided 1 − α/2 level of significance and let d₂ denote the number of events accumulated after the treatment effect onset. This implies that, under the standard delayed effect scenario, the piecewise weighted log-rank test with w₁ = 0 and w₂ = 1 is the most powerful weighted log-rank test, which is essentially the regular log-rank test taking into account only the events accumulated after the delayed onset. This result makes intuitive sense, and the heuristic argument is as follows. If the treatment effect is not revealed until t^*, then the earlier events before t^* would neither contribute to the detection of treatment effect nor comply with the proportional hazard assumption and should be ignored. In contrast, the later events after t^* do contribute and need to be included in the analysis exclusively. As the standard delayed effect scenario is most common in practice, we focus on this scenario thereafter.

3. APPLE method

It is clear that power in (3) is driven by the number of events after the delayed phase. However, in practice, it is the relationship between the power function and the number of subjects instead of the number of events that facilitate designing a study. Thus, the APPLE method is proposed to provide an analytic, close-form approach for the sample size and power calculation when the delayed effect is present.

Assume that the number of patients arriving a study of total duration τ follows a Poisson process with an intensity rate a. During the enrollment period [0, A] since randomization, the expected number of enrolled patients is equal to a×A. Consider an infinitesimal period of time [u, u+du], the expected number of patients in either experimental or control group who arrive during this period is equal to a × du/2 under equal allocation ratio. Assume that patients’ event times follow an exponential distribution with rate h_i1 before t^* and h_i2 after t^*, for group i ∈ {E,C} where h_C1 = h_C2 = h_C and let the corresponding F_i1(·) and f_i2(·), respectively, denote the cumulative distribution function and probability density function of exponential distribution. Among these patients, a proportion of F_i1(t^*) will experience an event during the delayed phase and the rest ${\int }_{t^{\ast }}^{\tau -u}{f}_{i2}(s)ds$ would survive beyond the delayed phase. Integrating over u, the total expected number of patients who would experience events before t^*, d̄_i1, and after t^*, d̄_i2, can be obtained as

$$\begin{array}{c}{\overline{d}}_{i1}={\int }_0^A\frac{a}{2}{F}_{i1}(t^{\ast })du,\\ {\overline{d}}_{i2}={\int }_0^A\frac{a}{2}{\int }_{t^{\ast }}^{\tau -u}{f}_{i2}(s)\mathit{dsdu}.\end{array}$$

Under the standard delayed effect scenario, it follows from d̄₂ = d̄_T2 + d̄_C2 that

$$a=2{\overline{d}}_2/(M_1+M_2),$$

where $M_1=e^{(h_{E2}-h_C)t^{\ast }}\{e^{-h_{E2}{t}^{\ast }}A-\frac{e^{-h}E{2}^{\tau }(e^{h}E{2}^A-1)}{h_{E2}}\}$ and $M_2=e^{-h_C{t}^{\ast }}A-\frac{e^{-h}{C}^{\tau }(e^h{C}^A-1)}{h_C}$. Therefore, the relationship between N and d₂ is constructed as

$$N=a·A=\frac{2{\overline{d}}_2}{M_1+M_2}·A$$

and the power of the study given the sample size N is obtained as

$${\mathit{Pow}}^{\ast }(N)=\mathrm{\Phi }\left\{\frac{1}{2}log({\lambda }_2)\sqrt{\frac{N(M_1+M_2)}{2A}}-Z_{1-\frac{\alpha }{2}}\right\}.$$ (4)

Under the general delayed effect scenario, the relationship between power and sample size is more complex and given in Appendix. Zhang and Quan [17] proposed an alternative approach for the sample size and power calculation which relaxes the assumption of log{h_C(t)/h_E(t)} = O(n^−1/2), although the results appear to be very similar with APPLE.

4. SEPPLE method

With an aim to compute the relationship between sample size and empirical power as well as verify the analytic approximation of APPLE, a simulation-based empirical power calculation algorithm, SEPPLE, is further developed. Given the sample size N, the enrollment duration A, the total study duration τ, the changing point t^*, and the baseline hazard h_C as well as the hazard for the experimental group after the delay h_E2, the simulation-based SEPPLE algorithm works as follows for each value of the assumed treatment effect λ₂ = h_C/h_E2:

• Step 1 Simulate patients’ enrollment times U based upon a Poisson process with intensity rate a = N/A;

• Step 2 Randomize patients to the experimental or control group and simulate patients’ event times T_λ2 from

  • T_λ2 ~ pexp (h_C, h_E2) for subjects in the experimental arm, where pexp (·) denotes piecewise exponential distribution function with rate varying at t^*;

  • T_λ2 ~ exp(h_C) for subjects in the control arm, where exp(·) denotes regular exponential distribution;

• Step 3 Define the observational times Z = min{T_λ2, τ − U} and the event indicators I = I{T_λ2 ≤ τ − U};

• Step 4 Apply the piecewise weighted log-rank test with weights determined by maximizing the power function under the pre-specified delayed scenario to compute the p-value p_λ2. Specifically, under the standard delayed effect scenario, the optimal weights w₁ = 0, w₂ = 1 are used.

• Step 5 Repeat Steps 1 to 4 for a large number of B times and compute the power for the given treatment effect λ₂ as the proportion of values p_λ2 that are less than or equal to α.

SEPPLE can provide a flexible framework to incorporate more complex enrollment process or event time distribution than APPLE. For example, SEPPLE can implement a non-homogeneous Poisson process for enrollment or a complex event time distribution. When both APPLE and SEPPLE assume same distributional assumptions on the enrollment process and event time, these two procedures should lead to similar results as they both rely on the piecewise weighted log-rank test.

5. Simulation study

To evaluate the properties of the proposed APPLE and SEPPLE methods, we carry out a wide variety of evaluations using both analytic approaches and simulation studies. These evaluations focus on two aims:

The first aim is to evaluate the effect of each pre-specified parameter on the sample size-power relationship empirically. Those prerequisite parameters include

• t^*: Hazard ratio changing point or treatment effect delayed duration since randomization;

• p: Proportion of subjects who will survive beyond t^*. Suppose that the event time follows an exponential distribution exp(h_C) during the delayed phase, the proportion p would depend on the baseline hazard h_C;

• λ₂: Hazard ratio during the post-delayed phase.

The second aim is to compare the performance of the proposed methods relative to the standard practice. When the delayed effect is present, the standard practice to account for the delayed effect in the sample size and power calculation is either ignoring the delayed effect or increasing the sample size to a certain extent as suggested by the commercial software package EAST [22]. As EAST, with the option for dealing with the delayed effect, has been widely utilized for trial design in practice, we compare the proposed methods with EAST under a hypothetical practical scenario.

In what follows, we assume the standard delayed effect scenario and a 0.05 level of significance. The SEPPLE method uses 10,000 replications in the power computation.

5.1. Evaluation #1

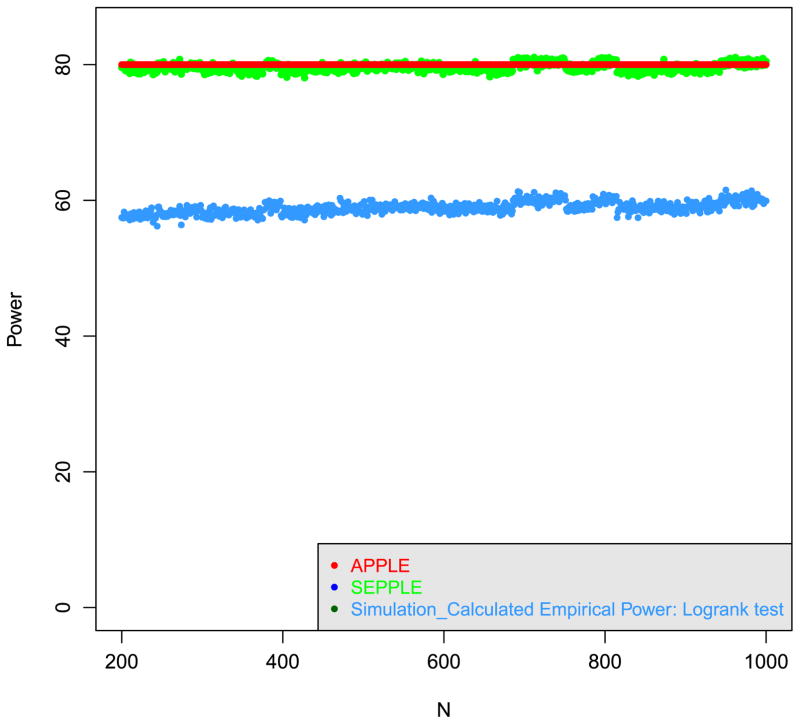
We first evaluate the power of SEPPLE and the regular log-rank test ignoring the delayed effect while the power of APPLE is fixed at the 80%. Assuming a delayed duration of 6 months and by the end of the delayed phase, 70% of subjects are still under study, we repeat the following steps for each given sample size N between 200 and 1000:

• Step 1 Fix the power of APPLE at 80% and back calculate the hazard ratio λ₂ required to achieve the target power;

• Step 2 For given λ₂,N, compute the power using the following methods:

  • SEPPLE method;

  • Standard simulation-based power calculation method based on regular log-rank test;

Figure 2 displays the sample size and power relationship for various methods. The red solid line serves as the reference line representing 80%power targeted by APPLE. The simulation-based SEPPLE method, as shown in the green curve, achieves a similar power as APPLE. In contrast, the regular log-rank test ignoring the delayed effect, denoted by the blue curve, is seriously under powered. This evaluation confirms that, first, the analytic power of APPLE approximates the empirical power of SEPPLE really well; second, ignoring the delayed effect leads to a serious loss of power under the parameter setting considered.

Figure 2.

Power of APPLE, SEPPLE methods, and regular log-rank test ignoring the delayed treatment effect given sample size and hazard ratio, where the power of APPLE method is set at 80%. The treatment effect delayed duration t^* = 6 months; proportion of subjects who can survive beyond the delayed phase p = 0.7 (i.e., h_C = 0.0019); Type I error rate α = 0.05.

5.2. Evaluation #2

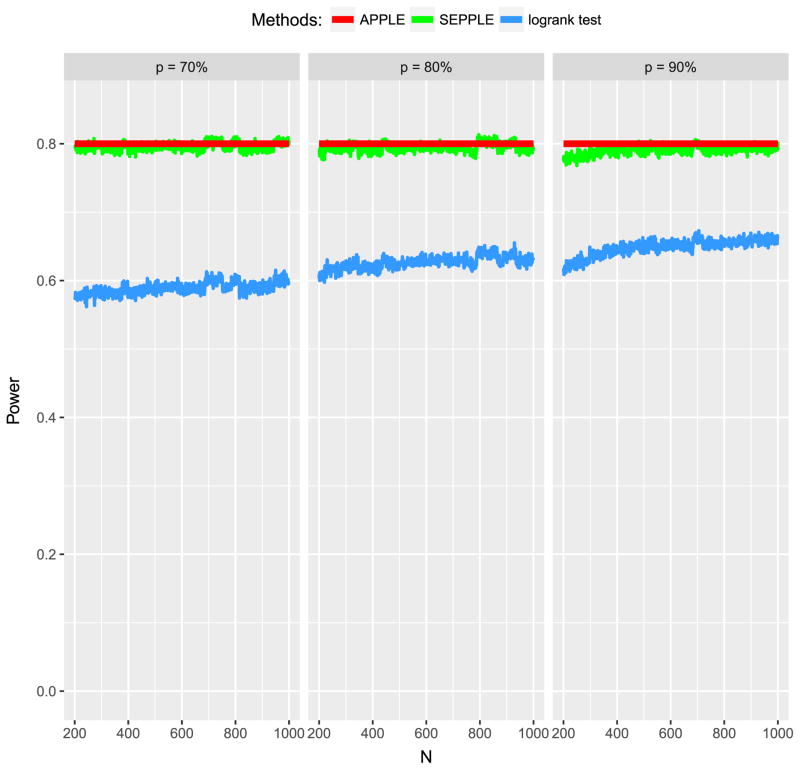
As revealed by the Sipuleucel-T study, only the events that take place after t^* contribute to the power of detecting a treatment effect. Thus, when the delayed effect is present, the power of the study would rely critically on the proportion of subjects who could survive beyond t^*, p. The second evaluation aims at examining the impact of p on the power by repeating the first evaluation under different values of p ranging from 70% to 90% while other parameter values remained constant.

As expected, the power loss due to ignoring the delayed effect becomes more apparent as p decreases (Figure 3). These results make intuitive sense. For example, when p = 90%, 90% of subjects would have events after the delayed onset and comply with the proportional hazard assumption, so the violation of the assumption due to only 10% of subjects is not severe and would not cause a serious loss of power. However, as p decreases to 70%, that is, 70% of subjects would experience an event after t^* under a constant hazard ratio λ₂ (λ₂ > 1), whereas 30% of subjects would die prior to t^* with hazard ratio λ₁ (λ₁ = 1), including all subjects into the standard log-rank test (blue curve) would severely violate the proportional hazard assumption and certainly cause a more serious loss of power.

Figure 3.

Power of APPLE, SEPPLE methods, and regular log-rank test ignoring the delayed treatment effect given sample size and hazard ratio under different values of proportions of subjects who can survive beyond the delayed phase p = 70%, 80%, and 90%. Total accrual duration A = 1 year; total study duration τ = 3 years; the treatment effect delayed duration t^* = 6 months; Type I error rate α = 0.05.

5.3. Evaluation #3

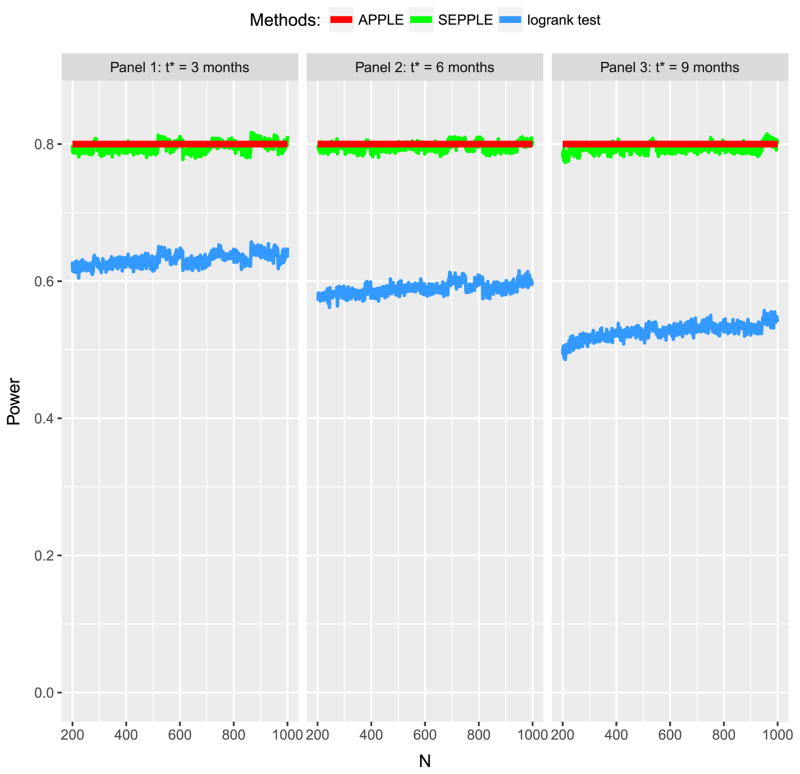
The changing point t^* certainly plays an essential role in the power calculation. As t^* gets larger, the violation of the proportional hazard assumption becomes more serious. The third evaluation focuses on the impact of t^* on the power by repeating the first evaluation using various values of t^* ranging from 3 months, 6 months to 9 months.

Figure 4 illustrates that when a 3 months of delay is observed as shown in the left panel, ignoring the delayed effect (blue curve) results in an approximate 20% loss of power; as the duration of delay prolongs to half year or 9 months, ignoring the delayed effect could lead to a more severe loss of power of 25% to approximate 30%, whereas SEPPLE in the green curve can maintain the power around 80% by properly taking into account the delayed effects of various degrees.

Figure 4.

Power of APPLE, SEPPLE methods, and regular log-rank test ignoring the delayed treatment effect given sample size and hazard ratio under different values of treatment effect delayed duration t^* = 3 months, 6months, and 9 months. Total accrual duration A = 1 year; total study duration τ = 3 years; proportion of subjects who can survive beyond the delayed phase p = 70%; Type I error rate α = 0.05.

5.4. Evaluation #4

Apparently, both APPLE and SEPPLE depend critically upon the pre-specification of t^*; but in practice, the true value of t^* is unknown. Then, what if the changing point t^* is mis-specified to be t_m in the design stage? Once the data is collected, the piecewise weighted log-rank test based on t_m is performed. Then, how much empirical power does the test have? In the fourth evaluation, the robustness of the proposed methods to the mis-specification of t^* is addressed under various scenarios.

To achieve a target power of 80%, we first compute the sample size required using APPLE when the changing point t^* is over-specified from the true 3 months to 6 months, or under-specified from the true 9 months to 6 months, respectively. Next, given the sample size, we calculate the empirical power of the piecewise weighted log-rank test based on t_m. For comparison purpose, we also evaluate the empirical power of the regular log-rank test ignoring the delayed effect. The empirical power is computed as follows. We first simulate the event times for the subjects in the experimental group under the true t^* (t^* ∈ {3, 9}) from a piecewise exponential distribution, where the hazards equal to h_C = −log(p)/t^* before t^* and vary to h_E2 = λ₂ × h_C after t^*. The event times for the placebo subjects are drawn from a regular exponential distribution with rate h_C. Second, we compute the p-values using the piecewise weighted log-rank test with w₁ = 0,w₂ = 1 based on t^m(t^m = 6), and the regular log-rank test ignoring the delayed duration. The aforementioned process are repeated 10,000 times to obtain the empirical power.

Table I respectively illustrates the impact of mis-specifying t^* in the sample size and power calculation using APPLE. For example, if the hazard ratio after t^* is λ₂ = 0.6, APPLE claims that 260 patients are sufficient to achieve the target power of 80% based on a mis-specified changing point at 6 months. The empirical study reveals that, given 260 subjects, the piecewise weighted log-rank test can achieve 79% power, close to the target, if the true t^* is at 3 months or 56% power if at 9 months, respectively. This finding is consistent with Zucker and Lakatos’s results [14], where the study power can be severely over-estimated when the true changing point t^* is above the specified. Nevertheless, despite being under-powered, the test accounting for the delayed effect is still more powerful than that ignoring the delayed effect, no matter if t^* is over-specified or under-specified.

Table I.

The impact of mis-specifying t^* on the power calculation using APPLE.

λ2	APPLE1	True t*2 = 3 months		True t* = 9 months
	Mis-specified tm5 = 6	PW-Logrank3 tm = 6 (%)	S-Logrank4 (%)	PW-Logrank tm = 6 (%)	S-Logrank (%)
0.6	260	79	76	56	40
0.64	335	79	76	56	41
0.68	441	78	76	57	42
0.72	599	78	76	57	42
0.78	1025	77	76	58	43

¹The sample size calculated using APPLE is based on the target power at 80%, the proportion of subjects who can survive beyond the delayed phase at p = 70%, total accrual duration A = 1 year, total study duration τ = 3 years, and Type I error rate α = 0.05.

²t^*: True hazard ratio changing time.

³PW-Logrank: Piecewise weighted log-rank test.

⁴S-Logrank: Regular log-rank test.

⁵t^m: mis-specified hazard ratio changing time.

5.5. Evaluation #5

The last evaluation aims at comparing the proposed methods with alternative approaches in terms of sample size and power calculation under a practical scenario when the delayed effect exists. Suppose an investigator would like to design a study with the power targeted at 80%. Various sample sizes are calculated using the APPLE method, regular log-rank test, and EAST software. The empirical power is also computed to verify how much power can be actually achieved given these sample sizes through a simulation study. Specifically, to obtain the empirical powers of APPLE and the log-rank test, the event times are repeatedly simulated under the standard delayed effect scenario and analyzed by the piecewise weighted log-rank test with $w_1^{\ast }=0,w_2^{\ast }=1$ or regular log-rank test, as alluded to in Section 5.4. The empirical power of EAST is given by the software.

Table II lists sample sizes required to achieve an 80% power under various size of treatment effect and proportion of subjects who can survive beyond t^*. For example, when the hazard ratio λ₂ is 0.7 and p = 90%, APPLE requires 922 patients; and a simulation study verifies that these many patients can achieve a nearly 80% power empirically when the delayed effect is indeed present. On the other hand, if the delayed effect is ignored, the standard practice using the regular log-rank test claims 691 patients being sufficient to achieve the target power, whereas the empirical power based on 691 patients is only 54% under the standard delayed effect scenario. EAST requires 1270 patients, that is, 348 more patients than APPLE to achieve the target power while accounting for the delayed effect. Although the empirical power reported by EAST based on 1270 patients is 80%, it is not clear how EAST accounts for the delayed effect behind the user-friendly interface, and an extra 348 patients would possibly become a waste of resources if the delayed effect is not properly or efficiently accounted for.

Table II.

Sample size and power calculation using the APPLE method, standard practice based on regular log-rank test (S-Logrank) and EAST software.

λ2	Consider t*		Ignore t*		EAST
	APPLE1	Empirical power (%)	S-Logrank	Empirical power (%)	EAST	Empirical power (%)
p = 90%
0.5	274	78	205	52	400	79
0.55	357	79	267	52	500	77
0.6	475	79	356	52	670	79
0.65	649	80	486	53	900	78
0.7	922	79	691	54	1270	80
p = 80%
0.5	174	79	120	46	270	79
0.55	227	79	157	46	350	80
0.6	302	80	209	47	450	78
0.65	415	80	287	47	630	80
0.7	590	79	409	48	870	79
p = 70%
0.5	149	79	93	39	260	80
0.55	195	80	122	40	330	80
0.6	260	79	163	40	430	80
0.65	358	79	225	41	570	78
0.7	512	80	322	41	810	79

¹The sample size calculated using APPLE is based on total accrual duration A = 1 year, total study duration τ = 3 years, and Type I error rate α = 0.05.

6. Some comments on the analysis

Once the trial is properly designed, the next question would be how to properly analyze the trial results. As indicated in the ICH E9 guideline (1998), the primary analysis method needs to be consistent with the method implemented in the sample size and power calculation. For studies designed by APPLE or SEPPLE, the piecewise weighted log-rank test is recommended for the primary efficacy analysis, where the weights and hazard ratio changing point ought to be consistent with that implemented in APPLE or SEPPLE.

7. Discussion

The proposed piecewise weighted log-rank test provides an intuitive and most efficient approach in analyzing therapeutic cancer vaccine studies with a delayed effect, where its efficiency is supported by analytic proof and empirical studies. Consequently, the corresponding APPLE and SEPPLE methods can account for the delayed effect, properly and efficiently, in designing such studies. In essence, the APPLE method is an analytic approach to derive the sample size and power relationship whereas the SEPPLE method is a numerical method to serve the same purpose. Under the pre-defined delayed pattern, APPLE clearly describes the sample size and power relationship provided that the distributional assumptions are reasonable; in contrast, SEPPLE provides a flexible framework that can implement more complex but realistic assumptions on the enrollment process or event time distribution in order to mimic practical scenarios.

Because both APPLE and SEPPLE rely on the piecewise weighted log-rank test, these procedures should lead to similar results under the same distributional assumptions. The simulation studies verify that the analytical APPLE approach can approximate the empirical SEPPLE method really well.

To apply the proposed methods, it’s critical to properly pre-specify the parameters such as the delayed pattern, hazard ratio, and baseline hazard based on prior knowledge and information. In particular, estimating the true delayed pattern accurately is challenging yet feasible. Besides relying on the biological or medical judgments on the mechanism-of-action of the therapeutic agent to determine the delayed duration, an investigator can obtain a good estimate of the true value using the preliminary data from Phase 1 and 2 studies. For example, if the clinical endpoint is overall survival, one may compare the hazard function of earlier phase trial(s) to that based on historical studies in order to assess whether survival improves after a certain time. Alternatively, if survival data are not available or historical data are not reliable, one can evaluate the change of certain immunological surrogate endpoints such as antibody level to obtain an estimate of the delayed duration.

Even though the parameters are estimated based on the best knowledge, the chance of mis-specification may still exist. The mis-specification of the delayed duration may result in an over-powered or under-powered study. As revealed in Section 5.4, the study power can be severely over-estimated when the true changing point t^* is above the specified. However, the test accounting for the delayed effect is still more powerful than that ignoring the delayed effect, no matter if t^* is over-specified or under-specified under the scenarios investigated. If prior knowledge and information are appropriately used to design a Phase 3 study with delayed effect, mis-specification of the delayed duration should be controlled within a reasonable range. In addition, sensitivity power analysis is very important while applying the proposed methods to account for the delayed effect. One may want to compute powers under various plausible delayed scenarios and compare those with the one with no delayed effect, in order to determine the necessity of applying proposed methods.

The proposed approach may be extended to account for the multi-phase delayed effect scenario. Specifically, when the hazard ratio follows a multi-phase piecewise constant function, the piecewise weighted log-rank test with optimal weights can be determined to maximize the study power based on Theorem 2.1. The generalized APPLE and SEPPLE methods for sample size calculation can be further derived. More research is warranted in this area.

Appendix

This appendix first derives the asymptotic distribution of the weighted log-rank test statistic S under the delayed effect alternative hypothesis with non-proportional hazard assumption and the condition log{λ(t)} = log{h_C(t)/h_E(t)} = O(n^−1/2); second, based on the asymptotic distribution, it maximizes the power of the test with respect to the optimal weight assignments. The most powerful piecewise weighted log-rank test can then be determined.

Following the definition in [8], the statistics from the conventional weighted log-rank test is

$$S=\frac{{\sum }_{j\in D}{b}_j\{X_j-p(t_j)\}}{{\left[{\sum }_{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}\right]}^{1/2}}.$$

The asymptotic distribution for S under the condition of log λ(t_j) = O(n^−1/2) can be obtained using Taylor expansion around zero:

$$\frac{{\sum }_{j\in D}{b}_j\{X_j-{\mu }_j\}}{{\left\{{\sum }_{j\in D}{b}_j^2{\mu }_j(1-{\mu }_j)\right\}}^{1/2}}-\frac{{\sum }_{j\in D}{b}_j\{log\lambda (t_j)\}p(t_j)\{1-p(t_j)\}}{{\left[{\sum }_{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}\right]}^{1/2}},$$ (A.1)

where

$${\mu }_j=\frac{n_C(t_j)h_C(t_j)}{n_C(t_j)h_C(t_j)+n_E(t_j)h_E(t_j)}.$$

Cox [23] showed that the first term in (A.1) has asymptotic standard normal distribution as long as the denominator is equal or converges to zero. Therefore, S follows an asymptotic standard normal distribution under H₀ : λ(t_j) = 1. Under the alternative hypothesis, S follows an asymptotic normal distribution with unit variance and non-centrality mean μ denoted by the second term in (A.1).

The proof of Theorem 2.1 involves Jensen’s inequality as follows.

Lemma 8.1 (Jensen’s inequality)

For a real convex function f (·), numbers x₁,…, x_n, and positive weights a₁,…, a_n,

$$f\left(\frac{\sum a_j{x}_j}{\sum a_j}\right)\le \frac{\sum a_{j}f(x_j)}{\sum a_j}.$$

Equality holds if and only if x₁ = x₂ = · · · = x_n or f (·) is linear.

Proof of theorem 2.1

Given the asymptotic distribution of S under the alternative, the power function can be further derived as

$$\mathit{Pow}=\mathrm{\Phi }\left(\mu -Z_{1-\frac{\alpha }{2}}\right).$$ (A.2)

For simplicity, we consider a one-sided 1 − α/2 level of significance. The power function of two-sided 1 − α level test can be easily obtained. In this paper, we assume no dropouts except the administrative censoring mechanism, because the investigators are encouraged by the agencies to follow up patients even after dropouts in practical oncology studies. The power function of the weighted log-rank test can be optimized by maximizing the non-centrality mean μ with respect to the weights { $b_j^{\prime }s$}, which can be obtained using Jensen’s inequality.

Let $a_j=b_j^{2}p(t_j)\{1-p(t_j)\}$ and $x_j=\{log\lambda (t_j)\}{[{\sum }_{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}]}^{1/2}/b_j$; then, square of the second term in (A.1) is

$$\begin{array}{l}{\mu }^2=\frac{{\left[{\sum }_{j\in D}{b}_j\{log\lambda (t_j)\}p(t_j)\{1-p(t_j)\}\right]}^2}{{\sum }_{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}}\\ =\frac{{\left[{\sum }_{j\in D}{b}_j\{log\lambda (t_j)\}p(t_j)\{1-p(t_j)\}{\left[{\sum }_{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}\right]}^{1/2}\right]}^2}{{\left[{\sum }_{j\in D}{b}_j^{2}p(t_j)\{1-p(t_j)\}\right]}^2}\\ ={\left(\frac{{\sum }_{j\in D}{a}_j{x}_j}{{\sum }_{j\in D}{a}_j}\right)}^2\\ \le \frac{{\sum }_{j\in D}{a}_j{x}_j^2}{{\sum }_{j\in D}{a}_j}\\ =\sum _{j\in D}{\{log\lambda (t_j)\}}^{2}p(t_j)\{1-p(t_j)\}={\mu }^{\ast 2}.\end{array}$$

The equality holds only when all x_j, j ∈ D, are equal, that is, b_j ∝ log λ(t_j), which implies that the mean μ is maximized when weights at the distinct event times are all proportional to the log of hazard ratios at those times.

Because log λ(t_j) is O(n^−1/2), using the central limit theorem, the maximum value of μ square is

$$\begin{array}{l}\sum _{j\in D}{\{log\lambda (t_j)\}}^{2}p(t_j)\{1-p(t_j)\}=\frac{1}{n}\sum _{j\in D}n{\{log\lambda (t_j)\}}^{2}p(t_j)\{1-p(t_j)\}\\ \to n\int {\{log\lambda (t)\}}^2\pi (t)\{1-\pi (t)\}V(t)dt,\end{array}$$

where function V(t) denotes the probability of observing an event at time t and π(t) the probability of observing the event in the experimental group, given as

$$\begin{array}{c}V(t)=P_E{f}_E(t)\left[1-H_E(t)\right]+P_C{f}_C(t)\left[1-H_C(t)\right]\\ \pi (t)=\frac{P_E\left[1-F_E(t)\right]\left[1-H_E(t)\right]}{P_E\left[1-F_E(t)\right]\left[1-H_E(t)\right]+P_C\left[1-F_C(t)\right]\left[1-H_C(t)\right]},\end{array}$$

where f_i(t), F_i(t) (i ∈ {E,C}) are the probability density and cumulative distribution functions (pdf and cdf) of event for the i^th group and H_i(t) is the cdf of censoring.

Therefore, the maximum asymptotic power is

$$\mathrm{\Phi }\left({\left[n\int {\{log\lambda (t)\}}^2\pi (t)\{1-\pi (t)\}V(t)dt\right]}^{1/2}-Z_{1-\frac{\alpha }{2}}\right).$$ (A.3)

Remark 1

b_j ∝ log λ(t_j) uniquely holds only for those events of at-risk subjects in both groups. If p(t_j) = 0 or 1−p(t_j) = 0, this event does not contribute to the log-rank test, and the weight at this time point does not affect the efficiency of the test.

Remark 2

Although Jensen’s inequality requires a_j > 0, that is, b_j > 0, b_j ∝ log λ(t_j) still holds for those j with λ(t_j) = 1 in terms of maximizing the second term in (A.1), because the denominator increases if b_j > 0 while the numerator stays the same. That is, b_j = 0 if λ(t_j) = 1.

Under the general delayed effect alternative

$$H_1:\lambda (t_j)=\frac{h_C(t_j)}{h_E(t_j)}=\{\begin{array}{ll}{\lambda }_1,\hfill & t_j\le t^{\ast }\hfill \\ {\lambda }_2,\hfill & t_j>t^{\ast },\hfill \end{array}$$

where λ₂ > λ₁ ≥ 1, the weighted log-rank test is most powerful when the weights b_j = w₁ if t_j ≤ t^*, b_j = w₂ if t_j > t^*, w₁/w₂ = log(λ₁)/log(λ₂), and w₁ +w₂ = 1, that is, w₁ = log(λ₁)/{log(λ₁)+log(λ₂)}, w₂ = log(λ₂)/{log(λ₁) + log(λ₂)}. Under the standard delayed effect scenario where λ₂ > λ₁ = 1, the optimal weights that maximize the power function can be easily solved as w₁ = 0 and w₂ = 1. In other words, the most powerful test under the delayed effect scenario is a piecewise weighted log-rank test with the optimal weights determined by the ratio of log hazard ratios before and after t^*.

Under the condition log(λ(t)) = O(n^−1/2) and equal censoring distributions (H_E(t) = H_C(T)), H_E(t) → H_C(t) (F_E(t) → F_C(t)), π(t) → P₁, as n → ∞, the maximum values of the non-centrality mean and power, π^* and Pow^*, can be further simplified as follows:

Under the general delayed effect scenario:

$$\begin{array}{c}{\mu }^{\ast }=\frac{1}{2}\sqrt{{\{log({\lambda }_1)\}}^2{d}_1+{\{log({\lambda }_2)\}}^2{d}_2},\\ {\mathit{Pow}}^{\ast }=\mathrm{\Phi }\left\{\frac{1}{2}\sqrt{{\{log({\lambda }_1)\}}^2{d}_1+{\{log({\lambda }_2)\}}^2{d}_2}-Z_{1-\frac{\alpha }{2}}\right\}.\end{array}$$

Under the standard delayed effect scenario:

$$\begin{array}{c}{u}^{\ast }=\frac{1}{2}log({\lambda }_2)\sqrt{d_2},\\ {\mathit{Pow}}^{\ast }=\mathrm{\Phi }\left\{\frac{1}{2}log({\lambda }_2)\sqrt{d_2}-Z_{1-\frac{\alpha }{2}}\right\},\end{array}$$

where we consider an equal allocation ratio P₀ = P₁ = 1/2, a one-sided 1 − α/2 level of significance and let d₁ and d₂ denote the number of events accumulated before and after t^*.