3D reconstruction of cystoscopy videos for comprehensive bladder records

Abstract

White light endoscopy is widely used for diagnostic imaging of the interior of organs and body cavities, but the inability to correlate individual 2D images with 3D organ morphology limits its utility for quantitative or longitudinal studies of disease physiology or cancer surveillance. As a result, most endoscopy videos, which carry enormous data potential, are used only for real-time guidance and are discarded after collection. We present a computational method to reconstruct and visualize a 3D model of organs from an endoscopic video that captures the shape and surface appearance of the organ. A key aspect of our strategy is the use of advanced computer vision techniques and unmodified, clinical-grade endoscopy hardware with few constraints on the image acquisition protocol, which presents a low barrier to clinical translation. We validate the accuracy and robustness of our reconstruction and co-registration method using cystoscopy videos from tissue-mimicking bladder phantoms and show clinical utility during cystoscopy in the operating room for bladder cancer evaluation. As our method can powerfully augment the visual medical record of the appearance of internal organs, it is broadly applicable to endoscopy and represents a significant advance in cancer surveillance opportunities for big-data cancer research.

1. Introduction

Endoscopy and its organ-specific derivatives (e.g., laparoscopy, colonoscopy, cystoscopy) play a powerful role in diagnostic imaging, surgical guidance, and cancer surveillance. Despite the rich information contained within endoscopy videos, the cumbersome nature of post-session video review drives the current clinical practice of condensing lengthy video data into a few still images and brief notes or drawings about the locations and appearance of suspicious lesions and scars. The limited data in the condensed record impedes quantitative and longitudinal studies of cancer physiology, disease process, or recurrence, and limits the impact of these data on clinical decision-making. The availability of complete organ reconstructions for other medical imaging modalities has been of powerful effect, leading to clinical advances in areas such as intraveneous injection, sleep apenea evaluation, and cervical and gastric cancer [1–4]. Thus, a comprehensive representation of the endoscopy data that enables straightforward and rapid review of a single endoscopy session or comparisons across several could better support the clinical decision-making process and enable new directions for cancer research. In this paper, we focus on developing comprehensive representations of cystoscopies, an important and clinically significant application: bladder cancer has the highest recurrence rate of all cancers and demands at least annual surveillance through cystoscopy to monitor recurrence. Hence, the ability to carefully and comprehensively review cystoscopy data could be an important advance in the management of this disease, which also bears the distinction as the most expensive cancer to treat over the lifetime of the patient [5].

Existing methods to create user-friendly representations of endoscopy videos include video summarization [6,7], panorama generation [8–10] and 3D reconstruction [11,12]. Summarization reduces the size of the video but still fails to localize frames in the context of their anatomical placement; meanwhile, panoramas present wide-field views but can distort the appearance of curved regions of the anatomy. Three-dimensional reconstructions that can capture both the 3D organ shape and appearance can enable depiction of full organs and localization of individual regions to anatomical locations in the organ. However, many existing approaches do so only in tandem with significant modifications to the standard clinical workflow (e.g., prescribed scan patterns [12]) or require additional hardware (e.g., structured light illumination projectors [13], time of flight cameras [14], optical position trackers [15]). These hardware requirements often come with a hefty infrastructure cost as well as a steep learning curve for clinician training and are therefore burdensome to adopt.

Other approaches for 3D reconstruction utilize standard clinical hardware with limited requirements on data collection, and research on this topic over the last decade has been summarized well by two review articles [16, 17]. Nonetheless, the demands of reconstructing a complete bladder from WLC video present challenges that have not yet been fully addressed by prior research: (1) The shape of the bladder is not known a priori because 3D medical images such as CT are not always collected prior to a cystoscopy; further, the bladder may change shape depending on its level of distension between imaging sessions. Approaches such as [18, 19] register the 3D reconstructed data to the 3D shape derived from a CT scan. (It should be noted, though, that while the ground truth shape of the bladder is not known, a shape prior such as a sphere can work to aid reconstruction [12]). (2) While the shape of the bladder is important for orienting the physician, the surface appearance will be more carefully scrutinized by the physician than the exact shape. Some 3D reconstruction approaches, however, present only a reconstruction of the shape of the organ ([20,21] and not the complete pipeline of converting the 3D reconstruction to a textured organ model. (3) In contrast with laparoscopy, the endoscopic light source is part of the endoscope, which means the surface illumination is constantly changing.

The varying lighting conditions make feature detection and matching brittle. Robust feature matching in the presence of outliers has been addressed by [21]; however, these approaches do not explicitly account for lighting variation, which can corrupt the description of features and introduce challenges for matching. (4) Finally, and perhaps most importantly, a cystoscopic video has a duration of several minutes and covers a large surface area relative to the area viewed in a single frame. As a result, a feature does not remain in the field of view for a large percentage of the video, which is problematic given that the key to reconstruction is efficiently detecting when a feature re-enters the field of view (i.e., a loop is formed) in order to reconstruct an accurate model. Several previous simultaneous localization and mapping (SLAM) and structure from motion (SfM) algorithms are demonstrated on a small number of images, which obviates the need for solving this problem. Other SLAM and SfM algorithms have been demonstrated with longer videos [20, 22, 23], primarily for laparoscopic applications. There, the field of view of a single image and the full reconstruction are more closely matched than in WLC. Other SfM papers make assumptions about the scan pattern in order to detect loop closures [12]. As such, these algorithms are not designed for efficient loop detection over a large set of features with an arbitrary scan pattern and are not well suited for WLC datasets from standard clinical procedures.

In this paper, we present the first method for dense 3D reconstruction of the bladder from white light cystoscopy (WLC) videos that uses standard clinical hardware and introduces only a minor modification to the standard clinical scan pattern. We address the four challenges that WLC presents for 3D reconstruction by (1) not utilizing any ground truth data to reconstruct the bladder surface, (2) presenting a complete pipeline to convert the cystoscopic images into a 3D textured model of the bladder, (3) developing an image preprocessing technique to remove lighting artifacts and thus strengthen feature matching, and (4) utilizing a structure-from-motion algorithm that efficiently can detect loops. Our treatment of these challenges via the presented algorithm pipeline should enable this strategy to be applicable for other 3D reconstruction problems with large fields of view.

A major enabling aspect of this work includes strategic design decisions regarding (a) the protocol for cystoscopic video collection, (b) the particular combination of state-of-the-art computer vision techniques used that includes a novel image preprocessing algorithm and (c) the end-to-end pipeline crafted uniquely for our application. The reliance on standard office tools makes this work easily and rapidly translatable for clinical deployment. To validate the reconstruction, we apply the algorithms to tissue-mimicking phantoms and to in vivo cystoscopy videos collected from bladder cancer patients undergoing surgery. Due to the widespread use of endoscopy in medical practice, this technique has promise to be expanded to other organs for which endoscopic surveillance is used, such as colon, esophagus, ureters, and stomach.

2. Algorithmic pipeline for 3D reconstruction

The starting point of our algorithm is a traditional workflow for dense 3D reconstructions. Specifically, the algorithm comprises four primary steps: (Fig. 1).

1. Image preprocessing. We select a subset of frames (“keyframes”) in the video and undistort the keyframes based on the calibrated camera model. A proprietary color adjustment algorithm processes each keyframe twice to generate distinct input images for later structure-from-motion and texture-reconstruction steps.

2. Structure-from-motion (SfM). Suitable keyframes are selected, from which interest points are detected, and feature descriptors for those interest points are matched between the images. An initial sparse point cloud – a representative set of 3D points (X_i) on the surface of the bladder – is generated, and camera poses (p_j) are calculated to describe the position and orientation of the cystoscope in each keyframe. This step uses an open-source SfM library [24], which was found to be optimal for refining the steps and configuration parameters of the pipeline.

3. Mesh generation. We generate a dense surface of the bladder based on the 3D point cloud from the previous step. The surface of the bladder is represented by a triangle mesh. This step combines a custom point cloud preprocessing technique with a Poisson reconstruction, a mesh-generation algorithm [25].

4. Texture reconstruction. The texture images (I_TEX), camera poses (p), and triangle mesh are used to map a surface texture comprising selected regions from the input images onto the triangle mesh, giving the 3D reconstruction the appearance of the bladder wall. We utilize a state-of-the-art package to achieve the output texture [26], whose quality is critically dependent on the prior image preprocessing steps.

Fig. 1.

Overview of the four-step 3D reconstruction algorithm. The gray inset highlights the sub-steps of the image preprocessing step. Black boxes indicate major steps and white boxes indicate the inputs and outputs for each step. SfM: Structure from motion TEX: texture reconstruction.

Individual steps of the pipeline were written in C++ and a Python wrapper was written to run the complete, automated reconstruction method.

2.1. Image preprocessing

The goal of the image-preprocessing step is to produce processed images to be used for the SfM (Step 2) and texture-reconstruction (Step 4) steps. This step involves four sub-steps: (A) distortion correction, (B) color processing, (C) mask generation, and (D) color adjustment. The output of this step is two sets of images, grayscale SfM images and color texture-reconstruction (TEX) images, which will seed Steps 2 and 4, respectively, of the overall algorithm (Fig. 1(b)).

The distortion-correction sub-step removes radial and tangential distortions that warp the images due to non-idealities endemic to the optics of the cystoscope based on the camera calibration. The camera is calibrated using images of a planar grid of circles with a T-shaped alignment mark [27], which is better suited for estimating the large distortions that exist at the edges of a circular field of view than its traditional counterpart of a fixed-size checkerboard pattern. In post-processing, a grid is fit to the center of the detected circles in the calibration images iteratively starting from the T-shaped alignment marks [27], and the grid is used to estimate the distortion and intrinsic camera parameters of the endoscope [28]. Note that one could handle time-varying intrinsic parameters with self-calibration techniques at the expense of significantly increased complexity and less robustness [29].

In the color-processing sub-step, we first separate the image into its red, green, and blue color channels (I_R, I_G, and I_B, respectively). The red channel approximates the lighting intensity at each pixel in the image, and thus this image can help to minimize variations in lighting across images due to the variation in the distance of and angle between the bladder wall from the cystoscope (and therefore from its light source); regions farther away appear darker because the light source becomes more diffuse with increased distance, and regions at a steeper angle with respect to the illumination direction appear darker as less light is collected from these locations. The red channel uniquely approximates the lighting intensity across the image in the bladder. Due to the shallow (starting less than 100 μm from the surface) and spatially heterogeneous location of blood vessels [30] as well as the significantly lower absorption coefficient of hemoglobin for red wavelengths (∼650 nm) compared with blue and green [31], the red channel contains limited vascular contrast (and thus just mimics the lighting intensity); whereas, the blue and green channels show a higher contrast vascular pattern. We also generate a second lighting intensity estimate: I_R−LP, the red channel image, which is low-pass filtered with a 2D Gaussian kernel with a standard deviation of 10 pixels. The Gaussian kernel parameter was tuned to provide a lighting-gradient-free image with sharp vascular borders for TEX images. The feature matching in the SfM step suffers when I_R−LP is used, so I_R is used for image preprocessing instead.

From the lighting intensity approximation, the mask-generation sub-step computes masks for images to be used as inputs to Steps 2 and 4 that identify which pixels are within the circular field of view of the cystoscope. Separate masks are generated for each of the SfM and TEX image datasets using thresholds that were manually tuned using several cystoscopy videos. The SfM mask (M_SfM) is computed by binarizing I_R using an intensity threshold of 10. The initial mask is then eroded with a disk of radius 30 to smooth the mask and eliminate holes. The threshold of 10 was selected by determining the value that separates the bright circular image from the dark (but often non-zero) pixels captured outside the circular image area. This image mask thus prevents detection of interest points well outside the circular field of view and allows interest points that have a spatial support that overlaps with the boundary of the circular field of view (i.e., have descriptors that are computed with pixels outside the mask) to be discarded. The initial mask for the texture images ( ${\mathbf{M}}_{\mathit{TEX}}^{\mathit{init}}$) is similarly computed by binarizing I_R−LP and applying a disk erosion; however, a higher binarization threshold (100 vs. 10 for M_SfM) is selected. This higher threshold eliminates dark regions of the image and was chosen heuristically to eliminate regions in the image with high noise to yield a higher-quality texture. Note that these dark regions are not masked for the SfM images, where it is preferable to have a field of view as wide as possible to detect interest points. Additionally, all pixels with values above 250 are set to zero to remove saturated pixels in both M_SfM and M_TEX. The final texture mask, M_TEX, is the convex hull of the largest contour of ${\mathbf{M}}_{\mathit{TEX}}^{\mathit{init}}$. The convex polygon-shaped mask prevents introducing “holes” (small, dark textureless regions) into the final texture.

In the last sub-step, the masks, color-channel images, and low-pass red image are used to generate the final output images. For the SfM images, we aim to achieve high-contrast images with consistent lighting to maximize the number of interest points that are extracted and that can be matched robustly across images. Variations in lighting can lead to corruption of feature descriptors due to the lighting gradients, and low contrast can lead to interest points being rejected due to lack of significant contrast. These issues are endemic to creating a grayscale image from the color image. Hence we choose instead to generate SfM images by normalizing the green-channel image (which has the highest contrast of the three image channels) by an approximate lighting intensity given by the red channel image (e.g., ${\mathbf{I}}_{\mathit{SfM}}^{ij}={\mathbf{M}}_{\mathit{SfM}}^{ij}{I}_G^{ij}/{\mathbf{I}}_R^{ij}$ for pixel (i, j)). Similarly, the final TEX images are computed by normalizing each of the channels by the approximation of the lighting intensity (e.g., ${\mathbf{I}}_{\text{TEX}}^{ij}={\mathbf{M}}_{\text{TEX}}^{ij}\left[\begin{array}{ccc}{I}_R^{ij}& I_G^{ij}& I_B^{ij}\end{array}\right]/{\mathbf{I}}_{R-\mathit{LP}}^{ij}$ for pixel (i, j)); the differing formulation of the two normalization equations reflects the large-area, grayscale nature of the SfM images compared to the smaller-area, color TEX images.

2.2. Structure from motion (SfM)

The SfM step estimates the structure of the bladder from the motion of the cystoscope camera. Specifically, this step generates camera poses (position and orientation) associated with the images of the cystoscopy and a point cloud – a set of 3D points that represent estimated points on the surface of the bladder that were visible in several images in the video. The point cloud is a sparse reconstruction of the surface of the bladder. We assume the bladder remains rigid, a valid assumption given the standard practice of distention of the bladder during cystoscopy.

Of the two main architectures that exist for SfM pipelines, we utilize a hierarchical rather than a sequential approach. Sequential SfM operates with video data and registers new keyframes to the 3D reconstruction acquired using the previous keyframes (i.e., the reconstruction successively expands), but requires additional building blocks for a robust reconstruction, such as a method to initialize the point cloud and camera poses. Hierarchical-SfM pipelines, in contrast, operate by first building several small reconstructions and then aligning them to form a larger reconstruction. This alignment step enables robust detection, handling of many loop closures and does not suffer from initialization challenges endemic to sequential-SfM pipelines. Although a hierarchical-SfM pipeline is more computationally intensive, our application does not require real-time performance, and the added robustness is important to avert the failures common in sequential SfM in cases where cystoscopic image quality may be poor.

The SfM step comprises four sub-steps: (1) keyframe selection, (2) two-view reconstruction (of camera poses and 3D points) through correspondence detection, (3) multi-view reconstruction, and (4) bundle adjustment, which refines the camera poses and 3D points. Keyframe selection involves a temporal downsampling of the original video sequence to eliminate redundant information captured in successive images, ensure a sufficient baseline between keyframes in the average case, and decrease computation time. We found by trial and error that temporal downsampling by a factor of 4 (i.e., selecting every fourth frame beginning with an arbitrary frame) from a 30 fps video sequence worked well to achieve good reconstruction with a minimal number of keyframes. More elaborate schemes (e.g., relying on image quality metrics such as “blurriness,” increasing the difference in camera position between sequential keyframes) may be devised in the future to further reduce the computational burden of downstream aspects of the algorithm.

Two-view reconstruction, multi-view reconstruction and bundle adjustment are implemented using an open-source SfM implementation by [24]. Two-view reconstruction of the camera poses and 3D points representing locations on the bladder wall is accomplished by detecting interest points in each keyframe and then identifying correspondences between related interest points from pairs of keyframes. A feature descriptor is extracted at each interest point and a correspondence is established if the descriptors of two interest points from two different keyframes are sufficiently similar. This process leads to robustly re-detectable interest points and stable descriptors despite changes in the image (e.g., due to perspective distortions after moving the camera, lighting variation, or compression artifacts). In our implementation, we use SIFT interest points and descriptors [32]. SIFT features, based upon image gradients, are invariant to image intensity, rotation, and scale and robust to affine transformations up to 30°. These properties of SIFT features are adequate for endoscopy images, as the bladder is typically imaged at an angle nearly normal to the surface. One main limitation of the endoscopy images is the lighting gradients caused by the endoscopy light source; however, our image pre-processing step enables meaningful interest points to be detected even in these conditions.

Unfortunately, since descriptors only capture a local “snapshot” around an interest point, the first list of correspondences computed will contain many outliers. We filter outliers using RANdom SAmpling and Consensus (RANSAC), which simultaneously estimates both the relative transformation (camera poses) between a pair of keyframes as well as their shared (inlier) correspondences [33]. RANSAC is an iterative algorithm that employs a hypothesize-and-verify scheme: to initialize the algorithm, five correspondences are selected as the consensus set. The essential matrix describing the transformation between camera poses is then iteratively computed using the five-point algorithm from the consensus set (hypothesis) [34], and the consensus set is updated by finding all correspondences that agree with the essential matrix (validation). If the size of the consensus set is sufficient (by trial and error, above 20 correspondences), this keyframe pair is deemed geometrically consistent.

To determine which pairs of keyframes to subject to RANSAC, for each query keyframe we use a vocabulary tree to generate a short-list of promising keyframes (typically 50) that might have viewed the same area of the bladder [34]. In brief, the vocabulary tree assigns the feature descriptors from all keyframes to leaves in its tree so that similarities between keyframes can be computed on the basis of having features that have been assigned to similar leaves; a leaf itself represents a set of shared properties between feature descriptors assigned to it, as determined by the dataset with which the tree was trained. The short-list of promising keyframes can be generated efficiently by comparing a single vector for each keyframe describing the arrangement of features in the vocabulary tree. Using this short-list, the number of times the more costly feature matching and RANSAC need to be applied is reduced from O(N²) for exhaustive matching to O(N), where N is the number of keyframes. In our experiments, we used a vocabulary tree pre-trained on a generic set of images rather than those specific to bladder data. While this was sufficient for our current datasets, we note it is possible that a vocabulary tree trained with cystoscopic images may yield better performance in the future. For each keyframe, a short-list of similar keyframes are extracted and used in the subsequent, computationally more expensive geometric-verification step (i.e., RANSAC).

The relative poses between camera pairs now known, each interest-point correspondence can be triangulated into a 3D point (X_i) by determining the intersection of the two rays that pass through the center of the camera and the interest point associated with the relevant keyframe. The relative camera pose between two images and associated 3D points is called a two-view reconstruction, as the structure of the sample and motion between images is determined for just two images. Given two-view reconstructions between many pairs of keyframes, the hierarchical-SfM pipeline then tries to combine reconstructions that share common keyframes into larger reconstructions. Specifically, we first find triplets of keyframes that result in consistent three-view reconstructions of the jointly observed interest points and then combine those triplets to form a single 3D reconstruction in a model generation step. All steps are formulated in a robust way in order to handle spurious results of previous processing steps (i.e., triplets that seem geometrically inconsistent will get removed) [24].

The hierarchical-SfM pipeline yields two outputs that are expressed in a single global coordinate frame: (1) a set of camera poses, which represents the position and orientation of the cameras corresponding to keyframes, and (2) a sparse point cloud, which contains a set of 3D points that correspond to positions on the surface of the bladder wall and are generated from triangulating 2D-interest-point correspondences into 3D. These outputs are then refined in sub-step 4, a bundle adjustment step [35,36].

Bundle adjustment performs a non-linear refinement of the locations of 3D points, camera positions and orientations such that the reprojection error between reconstructed 3D points projected into the camera and the measured 2D-interest-point correspondences in the image is minimized:

$$\underset{\mathbf{R},\mathbf{t},\mathbf{X}}{\text{min}}\sum _{(i,j)\in \mathrm{\Omega }}{\Vert {\mathbf{x}}_j^i-\mathrm{\Pi }\left(\mathbf{K}\left({\mathbf{R}}_i{\mathbf{X}}_j+{\mathbf{t}}_i\right)\right)\Vert }_2^2,$$ (1)

where i and j represent the index of the i^th camera and j^th 3D point, respectively, ${\mathbf{x}}_j^i$ is the 2D image point corresponding to camera i and 3D point j, Ω is the set of inlier correspondences, and Π : ℝ³ → ℝ² : Π(X) is the perspective projection function with R_i and t_i being the rotation matrix (orientation) and translation (position) of camera i. The optimization over the rotation matrices R_i is best performed with multiplicative updates R_i := Δ_iR_i, with incremental rotations Δ_i computed in the tangent plane to the manifold of the special orthogonal group using the exponential map [37]. For increased robustness, the L2-norm is usually replaced with a robust cost function such as the Huber cost or a truncated L2 cost [29].

The final output of the SfM step, therefore, contains a sparse 3D point cloud together with camera poses for each keyframe, which has been reconstructed up to a scale factor. The sparse point cloud is fed as an input to Step 3 of the pipeline, and the camera poses will be used as inputs to Step 4.

2.3. Mesh generation

The purpose of the mesh-generation step is to define a surface in the form of a triangle mesh from the sparse point cloud computed previously. The triangle mesh consists of a set of vertices (3D points), v_i, and faces (represented by three vertices), f_j. This representation allows us to leverage computer graphics tools to visualize and map a texture to the bladder surface. The mesh-generation step is implemented using the Point Cloud Library [38].

To generate a mesh, a typical approach densifies a sparse point cloud into a semi-dense point cloud. However, given the density of points in the sparse point cloud and the relative smoothness of the organ surface, a dense reconstruction was deemed unnecessary for this application. We selected the Poisson surface reconstruction algorithm to convert the point cloud into the triangle mesh due to its robustness to noise and tendency to generate watertight meshes, which effectively estimates a full organ surface even in the absence of imaging over the entire surface [25].

Our mesh-generation step begins by refining the point cloud through (1) statistical-outlier removal, which removes 3D points that lie more than two standard deviations from the average position of a neighborhood of 50 points, and (2) moving least squares, which sub-samples the point cloud to generate a smoother and more uniformly distributed point cloud using a search and sampling radius proportional to the physical size of the point cloud. The normal of each point is computed based on a function of neighboring points. Finally, Poisson surface reconstruction (with a tree depth of 6 chosen heuristically) generates a mesh using the surface normal and location of the 3D points, which are assumed to lie on the true surface of the bladder. The parameters for mesh-generation were chosen heuristically to achieve a smooth mesh that adequately captures the positions of the original point cloud from the SfM step.

A drawback of this method is that it is purely based on the geometry of the sparse 3D point cloud and ignores photometric errors: that is, inconsistencies between images that map to the same faces of the mesh and which could be used to refine the 3D point cloud. Thanks to bundle adjustment, the extracted surfaces were sufficiently accurate for our purposes.

2.4. Texture reconstruction

While Steps 2 and 3 capture the geometry of the bladder and camera poses, the appearance of the bladder is captured with a texture. The texture is stored as an image with mappings between mesh vertices and pixel coordinates. The “texturing” process overlays sections of real image data onto the 3D surface described by the mesh, much like wrapping a crumpled foil ball in printed paper. The texture-reconstruction step thus selects and combines input images (I_TEX) to generate an accurate, high-quality texture and, therefore, a high-quality bladder wall appearance.

To select the input images for each face from which the texture patches will be extracted, we first identify which faces can be seen by each camera. The mesh face can be projected onto a virtual camera (or equivalently onto the image plane of the camera) with exactly the same parameters as the real camera of a given keyframe based on the camera poses fed as inputs to this step. We assume that if the face is projected to within the boundaries of the image plane, it is visible to the camera.

In practice, the projected face will be visible in multiple keyframes. Hence, it becomes necessary to select a single image or to combine the pixels of multiple images to generate a high-quality texture for that face. As naive schemes such as averaging result in blurred textures or ghosting artifacts, we choose instead to use a view-selection scheme whereby we try to select the “best” input image for each face. The “best” input image for a given face will have the largest gradient magnitude, which will select for input images that are non-blurry and have a high density of pixels in the region corresponding to the given face. The image preprocessing step (Sec. 2.1) masks regions of the image that are noisy due to low SNR and likely to have large gradient magnitudes but poor image quality. To reduce the risk of introducing noticeable seams at the junction of neighboring faces sourced from different input images, we formulate a joint-optimization problem that selects an appropriate image for each face while favoring the appropriation of textures of neighboring faces from the same image. The optimization problem consists of a discrete-face-labeling problem and a subsequent blending of texture seams. We follow the approach presented by [26], which can be summarized as follows: Let K denote the total number of cameras. The labeling problem assigns a label l_i ∈ 1, . . . , K to each face f_i encoding the most appropriate image for defining the appearance of that face. Specifically, the labeling step minimizes the following energy:

$$E(l)={\mathrm{\Sigma }}_{f_i∊\text{faces}}{E}_d(f_i,l_i)+{\mathrm{\Sigma }}_{(f_i,f_j)∊\text{Edges}}{E}_s(f_i,f_j,l_i,l_j).$$ (2)

The energy formulation seeks to balance selecting high-quality labelings for each face (E_d) while minimizing seams between adjacent faces (E_s). Following [39], we compute the energy-data term E_d (F_i, l_i) for camera k as the gradient magnitude in image k integrated over the area of the projected face F_i. This formulation of the energy term ensures that there is a large and sharp projection area of face i in camera k, suggesting the camera that captured this region of tissue was in close proximity to the tissue surface and its optical axis was nearly to orthogonal to the surface normal. Additionally, the gradient magnitude favors high contrast, so the image is in focus and not blurry. We use the Potts model E_s = [l_i ≠ l_j] for the smoothness term. This term effectively creates large regions of contiguous faces that are textured by the same image. More complex, pairwise potentials could easily be introduced at the expense of higher computational demands (e.g., based on image-gradient information across the seam). Minimization of the aforementioned energy term results in a standard discrete-labeling problem with pairwise potentials that can be solved with graph cuts and alpha expansion [40]. After labeling the faces, the final step is to blend the texture at the seams to further minimize discontinuities. We follow the two-step procedure outlined in [26]: a coarse per-vertex color alignment is computed first, followed by Poisson image blending on each face.

The output of the texture-reconstruction step is a texture image (i.e., image that captures the appearance of the surface of the mesh) with a mapping between pixel coordinates and mesh vertices. Taken with the 3D mesh from the previous step, this generates a textured mesh – a bladder-shaped object with the appearance of the bladder wall.

3. Validation experiments

3.1. Data collection and calibration procedure

We utilized standard clinical equipment to collect all data: a 30° rigid cystoscope (4 mm OD, Stryker), xenon light source (Stryker X-7000), and endoscopic camera (Stryker HD-1488) with a resolution of 1280 × 720 pixels and a frame rate of 30 Hz. Additionally, we developed a data acquisition procedure that posed minimum disruption to the standard clinical workflow, and was an important precursor to obtaining high-quality images to seed the reconstruction. Three minor modifications to the standard cystoscopy workflow were necessary for our pipeline to be applied. First, given the use of a rigid cystoscope, to ensure that the camera parameters remained constant throughout the entire length of video, the endoscopist was instructed to (1) adjust the focus of the cystoscope only once after the cystoscope entered the bladder and (2) avoid introducing motion between the camera head and the cystoscope during the procedure, which causes the intrinsic parameters to change. That is, while the cystoscope is often rotated with respect to the camera to image during the cystoscopy in standard practice, in our acquisition protocol, the cystoscope and camera were consistently rotated together.

Second, to extract the highest quality images, the video was captured under the following conditions: (1) The entire cystoscopy procedure was recorded at the maximum camera resolution. (2) Once the cystoscope was inserted, the bladder was distended with saline to achieve a medium of uniform optical density through which to image the surface of the bladder and to achieve a near-rigid shape throughout imaging. The flow of saline was adjusted to remove debris from the bladder and to eliminate bubbles or turbulent particles that could obstruct images of the bladder wall. (3) After distention, the physician could adjust the focal length and the rotation of the camera head relative to the cystoscope, but otherwise kept these fixed throughout the rest of the procedure. The former condition is standard practice and the latter condition requires a only minor change to how the anterior wall of the bladder is viewed with a rigid cystoscope. (4) The cystoscope was kept within several centimeters of the bladder wall and slowly moved (at an approximate rate of 1–2 cm/s) during the imaging procedure to minimize motion blur. (5) To minimize drift in the reconstruction algorithm, the physician was asked to return to areas of the bladder previously imaged (i.e., to create “loops”). This was accomplished by imaging the posterior wall by first rastering with the fast-axis from neck to dome and then rastering in the orthogonal direction with the fast-axis from the left to right lateral wall. The same procedure was then repeated for the anterior wall. In standard practice, the bladder is also distended and a thorough visualization of the bladder wall is conducted; however, less care is taken to achieve the highest quality image at all locations of the bladder (since the physician has a general idea what he expects to see) and there is no need to systematically create loops in the scanning pattern.

Finally, following surveillance of the bladder wall, the physician performed a calibration procedure to determine the distortion and intrinsic camera parameters (Sec. 2.1). Without adjusting any camera parameters, images of a calibration target were collected at several angles and distances from the cystoscope. Both the careful scanning and the calibration procedure add a few minutes (3–5 min) to the standard cystoscopy procedure length, but the lengthening of the procedure is minor with respect to the entire endoscopic resection (typically 30 min – 2 hours). The reconstruction ran automatically after the relevant beginning and end frames of the cystoscopy and calibration steps were identified. Reconstruction was run with identical parameters across sections except for some slight tuning of parameters for three-view reconstruction in the SfM step, which could be automated in the future.

3.2. Phantom data collection

To validate the reconstruction algorithm, we created a phantom with a well characterized shape and surface appearance, similar to that reported in [11]. Datasets collected with the phantom enabled us to directly compare results with a ground truth reconstruction. The phantom consisted of a 3D-printed, 75-mm inner diameter semi-cylinder with a length of 100 mm onto which a high-resolution bladder image was color printed and affixed to the interior (“original semi-cylinder phantom”). A second phantom (“modified semi-cylinder phantom”) was created with small modifications to its texture and shape: specifically a few ink marks were added to the printed texture and a protruding ridge was added to the semi-cylindrical shape; the ridge shape remained the constant along the direction of the cylindrical axis. These modifications were meant to mimic the types of changes that could occur between cystoscopy sessions of the same organ in a patient with bladder cancer. The phantoms were imaged akin to the procedure described for the in vivo bladder examples: video data were collected by scanning the scope close to phantom wall in a raster pattern with the fast-axis first along the length of the cylinder and then along the circumference of the semi-cylinder. Notably, these data were collected in air rather than saline, and lighting was adjusted to minimize specular reflections.

3.3. Human data collection

Human bladder data were obtained from patients undergoing rigid cystoscopies in the operating room as part of their standard of care. This protocol was approved by the Stanford University Institutional Review Board and the Veterans Affairs Palo Alto Health Care System Research and Development Committee.

4. Results and discussion

4.1. Reconstruction of tissue-mimicking phantom datasets

We tested our reconstruction pipeline on datasets collected from a semi-cylinder phantom (“original”) and a modified version of it that contained small changes to the shape and appearance of the phantom (“modified”) (Fig. 2). The shapes of the phantoms roughly mimic the appearance, size and curvature of the bladder and, as they are known a priori, the ground truth shape and texture (pattern) information can be used to quantitatively and qualitatively evaluate the reconstruction results.

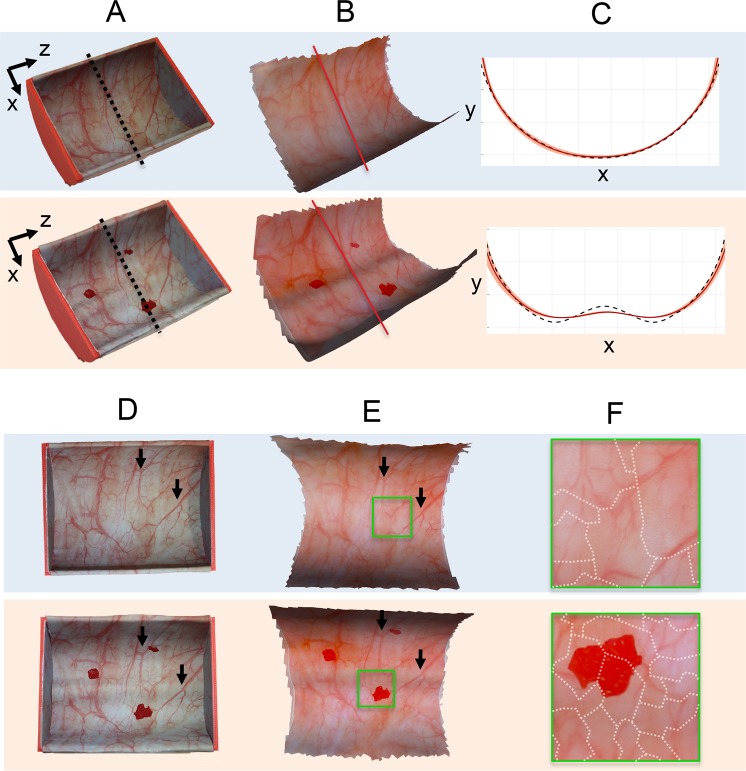
Fig. 2.

Phantom reconstruction results. Top row (blue background): original semi-cylinder phantom; bottom row (orange background): modified semi-cylinder phantom. (a) Standard digital camera images of the phantoms highlighting their shaped are compared with the (b) untextured reconstructed mesh. (c) Cross-sections of the expected mesh (dotted black line) and average reconstructed cross section (red) are compared. The pink region represents ±1 standard deviation of error about the average cross section. Each box of the grid represents 1 cm². (d) Standard digital camera images of the phantoms highlighting their surface appearance compared with (e) the reconstructed textured phantoms viewed from approximately the same camera angles. Black arrows are added to highlight similar features between the original and reconstructed images. Side walls of the phantom removed in (b) and (e) to accentuate the cylindrical portion. Green boxes indicate regions of texture shown in greater detail in (f), and emphasize the seamlessness between regions composed of different images. The dotted white lines in (f) indicate boundaries between mesh faces that are composed of different original images.

After reconstruction, the average reprojection errors, which describe the relationship between features extracted from 2D images and the projection of the calculated 3D representations into the image, were less than one pixel (0.80 and 0.79 pixels for the original and modified phantoms, respectively), suggesting a high-quality reconstruction [29]. A comparison between the ground-truth phantom shape and the reconstruction mesh shows that the shape of the phantom is reconstructed accurately in the structure-from-motion (SfM) and mesh-generation steps of the algorithm (Fig. 2(a) and 2(b)). Specifically, the original semi-cylinder phantom reconstruction takes on a semi-circular shape, as expected. The reconstructions of the modified and original semi-cylinder phantoms bear great resemblance, save for a small ridge along the bottom of the semi-cylinder in the former that corresponds to the actual protrusion below the textured paper designed to yield the modified form when the phantom was created.

To give a better sense of the comparison between the reconstructions and ground truth, the two meshes were aligned using an iterative closest point algorithm. The initial alignment estimate used a rigid transformation with a uniform scaling derived from manually selected correspondences. Fig. 2(c) compares the cross-sections of the two meshes along the z-axis which remains constant for the ground truth mesh. The root-mean-square errors (RMSE) between ground truth and the reconstructed mesh are 1.4 mm and 1.7 mm for the original and modified semi-cylinder phantoms, respectively. The RMSE is computed by interpolating each mesh at a fixed grid of x and z points and measuring the error in the y-axis. Because the mesh is symmetric, we also compared the variance in the mesh shape along the cylindrical axis. Using a mesh with a constant cross-section along the cylindrical axis equal to the average reconstructed cross-section (“average reconstructed mesh”), we computed the RMSE between the original and average reconstructed mesh:1.2 mm and 1.4 mm for the original and modified semi-cylinder phantoms, respectively. No clinically accepted tolerance exists for shape accuracy; however, given the recommended bladder distension of 50–75% during the procedure [41], an accuracy of about 1 cm is likely acceptable. Thus, while some of the curvature is not perfectly captured in the modified semi-cylinder, the variation is well within the acceptable tolerance for our application.

Figure 2(d) and 2(e) show a comparison between the texture captured by a single image from a standard digital camera with the reconstructed texture observed from roughly the same camera position and orientation. The similarity between the two images validates the accuracy of the reconstruction algorithm, as the reconstructed texture comprises approximately 50 images. Although a single digital camera can capture the entire semi-cylinder, this would be impossible with a cystoscope because a single image of the entire phantom captured with the cystoscope would be too dark or noisy. Not only are the original and reconstructed textures qualitatively very similar, but the reconstructed texture retains good contrast and sharpness of vasculature. Notably, the seams between images are nearly imperceptible over the majority of the bladder, as evidenced by the continuity of vessels across the boundaries of different images (Fig. 2(f)). This observation validates the high accuracy of the camera positions calculated in the structure-from-motion pipeline. Poor camera positions would cause inaccurate projections of images onto the mesh, leading to discontinuities at the boundaries of different images in the textured appearance.

4.2. Reconstruction of clinical datasets

To demonstrate the ability of the algorithm to work with standard clinical data, we collected cystoscopy videos from 21 patients undergoing a rigid cystoscopy prior to endoscopic resection of suspicious tumors in the operating room. The average length of the cystoscopy videos used for reconstruction was 6.0 ± 2.0 minutes, which corresponded to 2700 ± 900 frames given a frame rate of 30 fps with a temporal downsampling of four.

Figure 3 shows the output of the reconstruction pipeline for a representative dataset. The cystoscopy video (Fig. 3(a)) used in this example was 7:48 minutes in duration and required 80:33 minutes to perform the reconstruction. It is evident that the point cloud generated from the structure-from-motion (SfM) step (Fig. 3(b)) approximates an ovoid shape similar to a bladder. The sparse point-cloud reconstruction determined camera poses for 66.2% of the input images (excluding images when the cystoscope is entering or leaving the bladder through the urethra), which is an indicator of the robustness of the algorithm. The majority of keyframes (video frames selected to be used in the reconstruction) where camera poses could not be computed were in concentrated temporal segments of the video as opposed to sparsely sampled throughout the video. This pattern suggests the challenge with the reconstruction was due to the video quality, rather than the algorithm itself. Specifically, a few sections of the video where quality is poor due to dark images, fast motion, or obstruction with biopsy forceps do not have computed camera poses. Nonetheless the average reprojection error was 0.71 pixels, which suggests a high quality reconstruction.

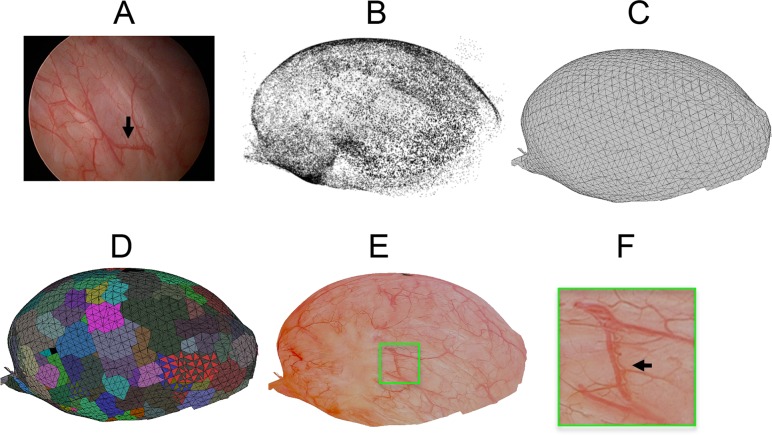
Fig. 3.

Output from individual steps of the reconstruction pipeline from a clinical dataset of human bladder: (a) a representative, original WLC image, (b) point cloud from the structure-from-motion step before outlier removal, (c) mesh from the mesh-generation step, and (d) labeled texture (faces with the same color are labeled with the same input image) and (e–f) textured mesh from texture-generation steps. The green box shows a similar region between subfigures (d–f) indicating clear continuity of vessels despite the use of multiple input images to construct this region. The green box is approximately the size of a single WLC image. Black arrows in (a) and (f) indicate similar regions of the bladder.

As expected, the mesh-generation step (Fig. 3(c)) preserves the ovoid shape of the bladder, and the texture-reconstruction step generates a high quality texture from several preprocessed images (Fig. 3(d), 3(e), and 3(f)). The texture-reconstruction step recovered a texture for 59% of the faces of the bladder mesh. This percentage provides an estimate of what surface area of the bladder wall was reconstructed. The inability to recover texture for the remaining faces is likely due to the lack of input for certain faces that were never captured with the cystoscope (as it is difficult to image the bladder neck with a rigid cystoscope), making texture recovery impossible for these faces. The missing region may also be due to the lack of loop closure between the edges of the region or imprecision in the reconstructed shape of the bladder.

The reconstructed texture maintains good continuity throughout the majority of the reconstruction, indicating that accurate camera poses were calculated (Fig. 4). The texture also has high vascular contrast with no apparent lighting artifacts. These characteristics of the texture are due to a proprietary image preprocessing step, which normalizes the image based on its estimated lighting variation and masks noisy, dark regions. Additionally, the texture-reconstruction step blends adjacent patches, which also contributes to the smoothness of the texture. Important features such as scarring and the 2–3-mm papillary tumor noted in the patient’s medical record are visible in the reconstruction (black circle in Fig. 4(c)).

Fig. 4.

Reconstruction from a clinical dataset of human bladder. Sub-figures show views from the (a) anterior, (b) posterior, (c) left lateral, and (d) right lateral walls. Black circle and arrow in (c) show regions of a papillary tumor and scarring, respectively. Regions that appear dark represent the interior of the bladder. Video 1 shows a fly-through of the full reconstruction.

Of the 21 clinical datasets collected, successful reconstruction was achieved for 66.7% of the datasets (n=14), where we define a successful reconstruction as one where at least 25% of the camera poses could be computed. All reconstruction failures that occurred are attributed to the SfM step, as the algorithm was unable to produce a sufficiently large reconstruction for some cases (this requires > 25% of camera poses). The primary source of failure (in n=5 datasets) was an insufficient number of extracted interest points (physical locations of features to be matched across keyframes), often caused by limited vessel contrast or significant debris in the bladder (759 ± 94 interest points per keyframe in successfully reconstructed datasets versus 488 ± 90 interest points in failed datasets). In the remaining failure cases (n=2), improperly calibrated cameras or significant motion of the camera head during image acquisition led to poor reconstruction. In part, these limitations can be overcome by developing a new protocol for data collection that includes bladder irrigation (leading to more interest points), slower scan speed (reducing motion artifacts) and more loops (reimaging of the same location in a closed pattern, leading to better image matching).

Among the successful reconstructions, 66.5% of the camera poses for interior bladder data were computed on average with a standard deviation of 20% and an average reprojection error of 0.71 ± 0.02 pixels; textures for 73% of mesh faces were able to be generated with a standard deviation of 12%, which given the tendency of Poisson surface reconstruction to produce a watertight mesh provides an approximation to the percent surface area of the bladder that is able to be reconstructed. As in the example reconstruction, many bladder reconstructions contained a large missing region around the bladder neck, which may be due to the lack of loop closure or imprecision in the reconstructed shape of the bladder.

4.3. Reconstruction algorithm run-time

Table 1 summarizes the run-time of the reconstruction pipeline for the human bladder example shown in Fig. 3 and the average statistics for all successfully reconstructed human bladder datasets. The average reconstruction requires 100 minutes; reconstruction times were roughly proportional to the number of images input into the SfM and texture-reconstruction steps, with the longest reconstruction times required for the SfM step. Additionally, datasets with lower thresholds to include triplets for three-view reconstruction required longer processing times. Additional steps that depend proportionally on the number of input images include image preprocessing, descriptor extraction steps, and image matching with vocabulary tree, among others.

Table 1.

Algorithm run-time of reconstruction pipeline for all successfully reconstructed datasets and example dataset from Fig. 4. Times given in MM:SS format

	Average (n=14)	Example
Num. images	2567 ± 664	3498
Num. reconstructed images	1668 ± 612	2317
Image preprocessing
for SfM images	03:00 ± 01:03	3:59
for TEX images	2:16 ± 00:24	2:28
SfM
Feature extraction	02:14 ± 01:56	7:02
Two-view reconstruction	26:16 ± 10:15	32:01
Three-view reconstruction	26:30 ± 33:00	6:47
Model generation	37:28 ± 39:11	19:59
Mesh generation	00:07 ± 00:05	0:26
Texture reconstruction	1:07 ± 0:27	7:51
TOTAL	100:00 ± 88:45	80:33

Although the current algorithm requires significant time for processing, the current timing is sufficient for the current clinical workflow: it is not imperative to use these reconstructions in interactive-time as they merely need to serve as visual medical records that can be reviewed before the patient’s next procedure. In the future, the processing time of the SfM algorithm or texture reconstruction code could be further reduced by taking advantage of the temporal ordering of images in the video sequence.

5. Conclusion

We demonstrate a method for generating high-quality 3D reconstructions of the bladder wall. The proposed algorithmic pipeline and image acquisition protocol support the use of standard clinical equipment and require only minor modifications to the standard imaging workflow. Hence, the pipeline can successfully reconstruct real clinical data obtained from in vivo environments.

The experience of the current implementation highlights several important points. First, obtaining high-quality images is paramount to good performance. That said, clutter-free, deformation-free imaging conditions with high vascular contrast may be challenging to achieve in some cases, leading to poor contrast or disjointed textures. Some such challenges could be addressed with real-time feedback to alert the physician to improve the image-acquisition quality (e.g., better irrigate the bladder), with image-based depth map computation [42,43], with hardware modifications [14,15], or with additional assumptions on the bladder shape and location of acquired images. A second and related point is that image pre-processing alone may not be sufficient to generate high-quality textures from poorly acquired images, although optimization of the camera positions and 3D mesh vertices may provide a means to ameliorate some inadequacies. For example, a surface-refinement step using photometric costs [44] or geometric costs (e.g., forcing the reconstruction to fit to a model bladder-shape) could be added in the future. As for the efficiency of the algorithm, the computational time is currently unsuitable for real-time surveillance, but extensions to utilize an initial reconstruction as a prior with SLAM techniques could allow for real-time support. Finally, the current reconstruction pipeline notably produces a large missing region around the neck of the bladder. In the future, co-registration of the bladder reconstruction to a standard bladder using a shape prior or anatomical regions as correspondences (e.g., ureters, neck, dome) can address this.

The proposed algorithm can also serve as the foundation for surgical planning, quality assessment of the procedure, optical annotation, and integration with other optical technologies (e.g., confocal microscopy, optical coherence tomography). A longitudinal record of the bladder appearance can enable new quantitative studies of the time-varying appearance in the bladder wall: for example to predict the location of early tumors or to stratify patient outcomes. The reconstructions presented in this work are based on rigid cystoscopies, but the proposed method is extendable to flexible cystoscopes, which are able to achieve full coverage of the bladder (e.g., bladder neck). Importantly, the shape-agnostic nature of the algorithm may make it extendable to reconstructions of other organs using their respective endoscopy derivatives.

Funding

KLL was supported by an NSFGRFP fellowship and NSF IIP-1602118, JCL was supported in part by NIH R01 CA160986, and RA was supported by the Max Planck Center for Visual Computing and Communication.