Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Jul 20.
Published in final edited form as: Vision Res. 2013 Nov 8;96:140–144. doi: 10.1016/j.visres.2013.10.016

Contour interaction in foveal vision: A response to Siderov, Waugh, and Bedell (2013)

Daniel R Coates 1, Dennis M Levi 2,*
PMCID: PMC5518604  NIHMSID: NIHMS882433  PMID: 24216008

In both peripheral and foveal vision, the ability to recognize a letter may be degraded by nearby contours. In peripheral vision, this contour interaction operates over a large distance, where the targets and flanking contours are well separated, and is often referred to as ‘crowding’ (see Levi, 2008; Whitney & Levi, 2011 for reviews). In peripheral vision, the extent of contour interaction is more or less independent of target size, and is proportional to E, the target eccentricity (being as much as 0.5E – Bouma, 1970; Pelli, Palomares, & Majaj, 2004; Toet & Levi, 1992). These effects occur with both high and low contrast stimuli in peripheral vision.

In normal foveal vision, however, earlier studies suggest that contour interaction is limited to small (near the resolution limit) high contrast stimuli and vanishes with low contrast targets (Strasburger, Harvey, & Rentschler, 1991; Simmers, Gray, McGraw & Winn, 1999). However, a recent study (Siderov, Waugh, & Bedell, 2013) measured contour interaction for targets at three different contrast levels, and concluded that contour interaction for foveal targets indeed occurs within a fixed angular zone of a few minutes of arc, regardless of the size or contrast of the acuity target. This conclusion seems to conflict with previous work showing that the zone or extent of contour interaction for low contrast Gaussian and Gabor targets (Levi, Klein & Hariharan, 2002; Hariharan, Levi & Klein, 2005) is proportional to target size, and thus reflects simple overlap masking.

Here we reanalyze the data of Siderov, et al. using fits to their spacing-vs.-performance curves, and show that the slopes of these functions differ based on condition. This technique can parsimoniously capture the modulation of extent and magnitude the authors describe in a more recent paper employing low-luminance stimuli (Bedell et al., 2013). An outcome of this method is that it shows how the present results, as well as others previously thought to be in conflict, are actually compatible with both a small fixed angular extent for small targets and one that is proportional to target size for larger, low contrast targets, a dichotomy that has been previously described (Ehrt & Hess, 2005).

Specifically, Siderov et al. measured letter identification performance (% correct) for Sloan letters at three different contrasts. The sizes of the lower contrast letters were increased (relative to the high contrast letter), so that the unflanked identification rate was between 80% and 94% correct for each of the three different contrast/size letters. They argue that when percent correct identification is plotted against the angular separation between target and flanker edge-to-edge separation (in minutes of arc) the three different target size/contrast curves overlap, indicating a fixed angular crowding zone. However, close inspection of their results suggests that the overlap is not perfect, and there is no a priori reason to expect edge-to-edge angular separation to yield similar curves. The three rows in Fig. 1 illustrate three ways to analyze their data; specifically (from top to bottom): as a function of edge-to-edge nominal spacing (in units of stroke width), edge-to-edge absolute spacing (in minutes of arc), and center-to-center absolute spacing (in minutes of arc).

Fig. 1.

Fig. 1

Open in a new tab

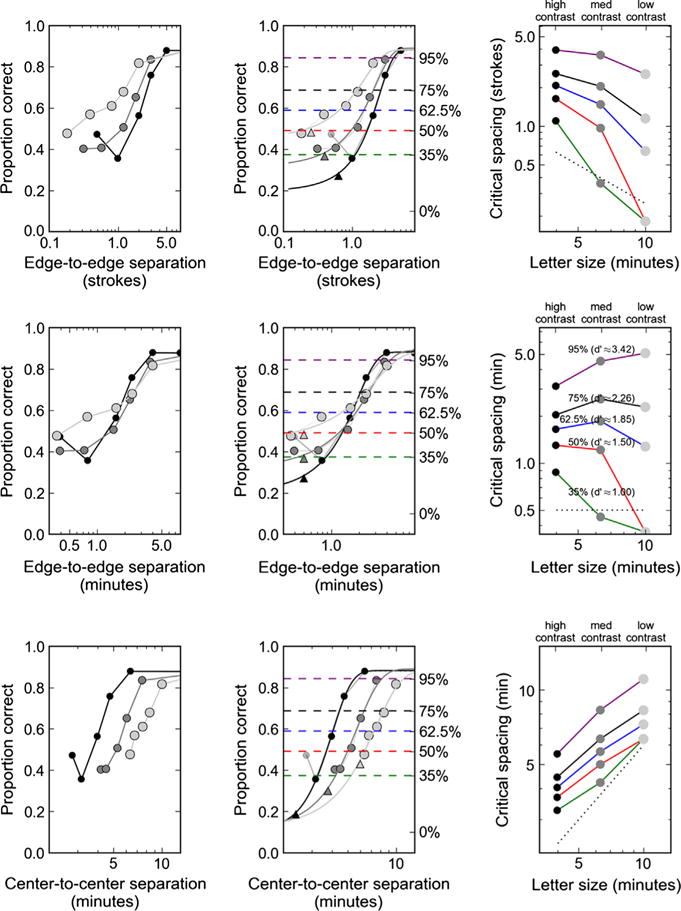
Data of Siderov, Waugh, and Bedell (2013) are replotted and analyzed in three different ways: Top row: as a function of edge-to-edge nominal spacing (in units of stroke width); Middle row: as a function of edge-to-edge absolute spacing (in minutes of arc); Bottom row: as a function of center-to-center absolute spacing (in minutes of arc). The left column simply replots the data. The middle column shows the cumulative Gaussian fit to the data. The right column shows the critical spacing (CS) as a function of letter size/contrast level (low, medium, high) at five different percent correct criterion levels/d’ values (see text for details). Note that the rightmost point of the 50% curve was extrapolated from the data, and the rightmost point cannot be extrapolated with the 35% criterion. In these plots, target size and contrast are coded by symbol contrast, with the smallest, high contrast targets shown by the black circles and the largest lowest contrast targets shown by the gray circles. The middle column shows the five criterion levels as dashed lines color-coded to correspond to the appropriate curves in the rightmost column. Triangles in the middle column (bottom row) indicate adjacent target and flankers. The black dotted lines in the rightmost column indicate either adjacent target and flankers (bottom row) or stimuli separated by exactly 0.5 min of arc (top two rows).

It is clear from inspection that with center-to-center absolute spacing (bottom), the three curves are shifted along the separation axis, with the smallest (highest contrast) target (black symbols) showing the smallest zone of interaction and the largest (lowest contrast) target (light gray symbols) showing the largest zone. Note that Siderov et al. did not plot their results in this way; rather they plotted it in terms of stroke widths and edge-to-edge separations (similar to the top two panels in the left column of Fig. 1). They note that plotting center-to-center separations would result in non-overlapping functions that are similar to those obtained when plotting in stroke widths; however, as can be seen by comparing the top and bottom left panels of our Fig. 1, the order is reversed. Siderov’s graphs (and the top left panel of Fig. 1) show the large/low contrast target having the smaller zone (in stroke widths), ours (bottom left panel of Fig. 1) show it having the largest zone (in angular center-to-center separation). Similarly, Danilova and Bondarko (2007) found that target-flanker critical spacings reduced as target size increased. However, they also based their analysis on edge-to-edge spacing. With center-to-center spacing, the critical spacings remain consistent across sizes, an effect that has been shown in numerous other studies (Levi & Carney, 2009, 2011; Pelli, Palomares, & Majaj, 2004; Pelli & Tillman, 2008; Tripathy & Cavanagh, 2002). We describe reanalysis of their data (and that of many other investigations) below.

A principled way to quantify the zone of contour interaction is to fit a parametric function to the percent-correct vs. flanker separation curve and identify the separation yielding a criterion level of performance. This separation is often referred to as the critical spacing (CS). We have performed this fit in Fig 1., using a cumulative normal function following many previous studies (e.g., Levi, Hariharan, & Klein, 2002; Tripathy & Cavanagh, 2002). The left column of Fig. 1 replots the data, simply connecting the points with lines. The middle column shows the fitted functions, and the rightmost column shows the resultant critical spacings at five different criterion levels.

The fits to the three curves (middle column of Fig. 1) are very good: R2 of the three curves are (from high to low contrast): 0.998, 0.985, and 0.984, respectively, for all three measures of spacing.

The percentages shown near each curve in the rightmost middle panel indicate the criterion adjusted percentages, interpolated between the minimum and the maximum of each function, with the minimum fixed at 0.10 (the guess rate for Sloan stimuli) and the maximum defined as the unflanked proportion correct. The corresponding d′ values are also shown in parentheses. Note that the data point for the closest flank in the high-contrast curves has been omitted from the fit, as there is evidence of facilitation when the flankers are very close, an effect occasionally seen in some, but not all, crowding experiments.

The notable feature of the critical spacings interpolated for the edge-to-edge measure used by Siderov et al. (right middle panel) is the following observation. For a criterion around 75%, the curves correspond very well, as shown by Siderov et al. However, for stricter criteria, the critical spacing increases as a function of size/contrast, while for laxer criteria the critical spacing decreases. This is due to the differing slopes in the functions fits shown in the middle panel. An additional point of note is that the lower asymptote of Siderov’s data for all sizes and contrast levels is around 40% (d′≈ 1.18), whereas the guess rate expected for Sloan letters would be 10%. This is also true of more recent work from this group. Specifically, Bedell et al. (2013) have argued that the extent (but not the magnitude) of foveal contour interaction is independent of background luminance.

None of the three rows in Fig. 1 is fully satisfying. However, a key observation is that the slope of the performance vs. spacing curves is different across the three size/contrast conditions. The center-to-center measure (bottom row) provides a hint to a possible solution, as these curves appear to have similar slopes as a function of log spacing. Following an approach similar to Latham and Whitaker (1996), a linear function of stimulus size was found such that shifting the abscissa of each curve by the appropriate amount (i.e., dividing the x-values) yielded a single canonical cumulative Gaussian function. A simultaneous nonlinear least squares minimization optimized four parameters values: the standard deviation and mean of the cumulative Gaussian, and two coefficients defining the divisor as a linear function of the target size. These parameters are dependent, so the cumulative Gaussian could be arbitrarily located such that the shifting divisor was simply (size + C) for some constant C. A grid search of sets of the possible parameter values confirmed that there was a single global minimum best value. Fig. 2 shows the canonical cumulative Gaussian for these data, having standard deviation = 0.18 and mean = 0.48. The standard deviation (sigma) for a cumulative Gaussian is approximately the reciprocal of the slope of a similar Weibull function, meaning this psychometric function has a very reasonable “slope” of around 5. The units of the abscissa represent a ratio, the center–center spacing divided by the letter size plus the constant 3.68 (all in minutes). The data points shown are the original data of the three sizes/contrast conditions translated using this ratio. When the ratio is one, the points are outside the crowding limit. One singularity is the x value where the edge-to-edge curves intersect, visible in the inset. Since the center–center spacing for Sloan letters flanked by bars is 3/5 * letter size + edge-to-edge separation, when the edge-to-edge separation is 3/5 * 3.68 = ~ 2.21 min, the numerator and denominator have the same ratio for any size.

Fig. 2.

Fig. 2

Open in a new tab

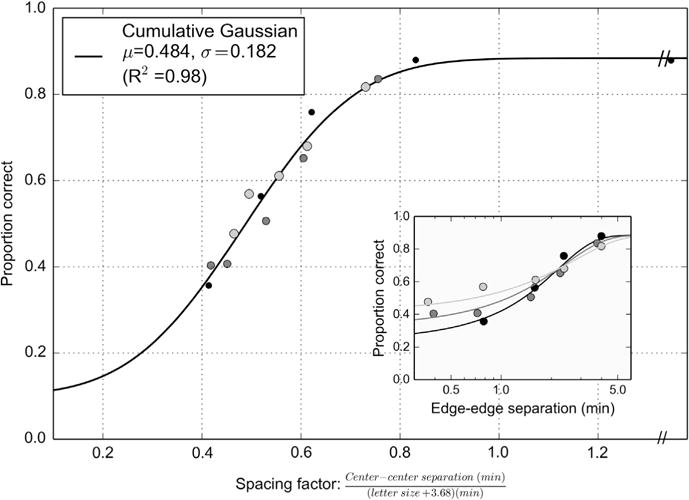
The fit of a canonical cumulative Gaussian to the Siderov data. The units of the abscissa represent a ratio, the center-center spacing divided by the letter size plus the constant 3.68 (all in minutes). The data points shown are the original data of the three sizes/contrast conditions translated using this ratio. See text for details.

With this formulation performance at any arbitrary size/spacing condition can be predicted. There are several theoretical implications that follow. First, the psychometric functions for foveal stimuli do indeed have some dependence on character size, although with small characters and character spacings, performance is primarily dictated by the constant term (3.68′). The change in slope means that care must be taken when measuring critical spacing, as indicated above. The observation by Bedell et al. (2013) concerning the reduced magnitude of the crowding effect in a low luminance condition can be captured by the mathematical formulation, and this effect is apparent in the present data as well. Fig. 3 shows a full grid of predicted percent correct performance values extrapolated from the psychometric functions fitted to the data of Siderov, Waugh, and Bedell (2013). Each point in the grid indicates a single letter size (x-axis) at one edge-to-edge separation (y-axis). A full predicted psychometric function can be read from bottom to top for a given letter size. The dashed line indicates the ordinate where target and flanker abut (edge-to-edge spacing is zero). Interestingly, the minimum percent correct predicted on this line increases as stimuli get larger, as observed in the experimental data.

Fig. 3.

Fig. 3

Open in a new tab

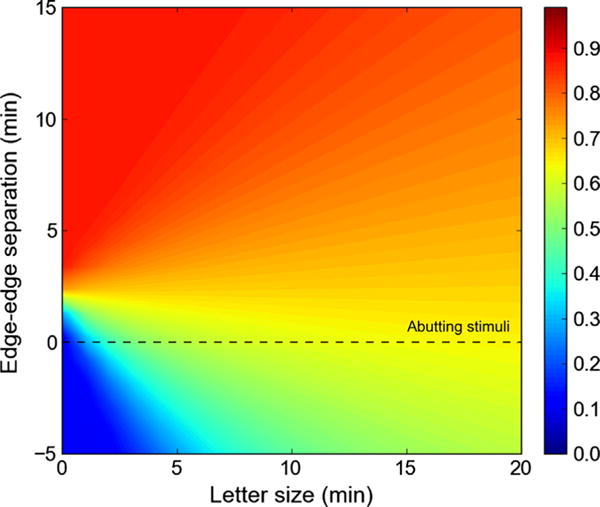
The full grid of predicted percent correct performance values extrapolated from the psychometric functions fitted to the data Siderov, Waugh, and Bedell (2013). Each point on the grid indicates a single letter size (x-axis) at a given edge-to-edge separation (y-axis). A full predicted psychometric function can be read from bottom to top for a given letter size. The dashed line indicates the ordinate where target and flanker abut (edge-to-edge spacing is zero).

To place the fitted data from Siderov et al. in context we plot data from their study (solid black circles) along with a number of other studies that have measured foveal contour interaction in Fig. 4. Specifically, Fig. 4 shows the critical spacing (based on center-to-center spacing in minutes of arc) vs. target size. The open circles and squares show results using low contrast Gaussian and Gabor targets over a wide range of sizes (from Levi, Klein, & Hariharan (2002) and Hariharan et al. (2005)). The other symbols show results from Flom, Weymouth, and Kahneman (1963), Danilova and Bondarko (2007), Toet and Levi (1992) and Hess, Dakin, and Kapoor (2000). These authors use a broad range of criteria. The results are consistent with a two-mechanism descriptive model in which the critical spacing for foveal contour interaction occurs (CS0) is a small fixed spacing when the target size (S) is small (< about 5 arc min), and proportional to target size for S > than about 5 arc min. In this ‘hockey stick’ model, there is a small range of target sizes in which flankers result in genuine foveal crowding. Like peripheral crowding, this zone is more or less independent of target size. For targets that are larger than the fixed crowding zone, nearby flankers result in masking (Hariharan, Levi, & Klein, 2005; Levi, Klein, & Hariharan, 2002; Pelli, Palomares, & Majaj, 2004). This masking occurs over a distance that is proportional to target size. Indeed, the gray dotted line shows the fit of this model, and the triangle along the abscissa shows the critical target size (Sc) derived from this bi-linear fit.

Fig. 4.

Fig. 4

Open in a new tab

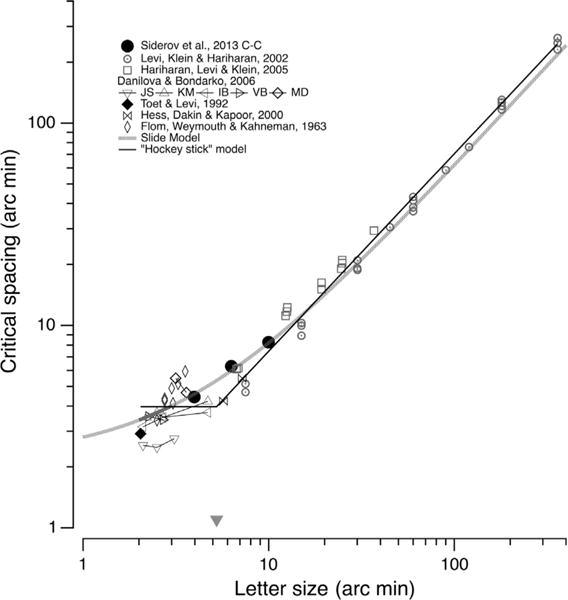
Critical spacing (CS - based on center-to-separation in minutes) vs. letter size. Solid black circles replot the critical spacings of Siderov et al., from figure. The other symbols show data from several other studies plotted in the same way. The black line shows the fit of a simple 2-mechanism model in which the critical spacing for foveal contour interaction occurs (CS0) is a small fixed spacing when the target size (S) is small (⪅ 5 arc min), and proportional to target size for S > than ≈ 5 arc min. The gray triangle near the abscissa shows CS0. The gray line is the prediction based on the analysis shown in Fig. 2 (using c–c critical separation = 0.6* (size + 3.68).

Our two-mechanism model may help to explain several of the mysteries surrounding foveal contour interactions, which have often seemed elusive. Firstly, as noted earlier, a number of studies using low contrast targets suggest that there is little or no foveal crowding. In these cases, the low contrast targets are inevitably larger than Sc. In contrast, studies using high contrast targets inevitably report CS0 ≈ 3–4 arc min (as seen from the flat region of the bi-linear fit in Fig 2). This fixed small (3–4′) foveal crowding zone is also seen for Vernier acuity with thin lines (Levi, Klein, & Aitsebaomo, 1985; Westheimer & Hauske, 1975) and for line orientation discrimination (Andriessen & Bouma, 1976). The data of Siderov et al. appear to fall in both camps. Their smallest/high-contrast target is smaller than Sc, and CS0 falls within the range of other studies using high contrast targets, whereas the two larger/lower contrast targets are larger than Sc, and show larger critical spacings, consistent with a critical spacing approximately proportional to target size.

For targets larger than ≈ 5–6 arc min, CS is ≈ proportional to target size. Flom, Weymouth, and Kahneman (1963) proposed that foveal contour interaction occurs when there is an overlap between the target and the flanks in the same neural unit e.g. cortical receptive field and/or hypercolumn (Levi, Klein, & Aitsebaomo, 1985). This explanation predicts that contour interaction would occur over a large range of target sizes and that the extent of crowding would be proportional to the target size (as shown in Fig. 4). This explanation implies that the contour interaction is essentially overlap masking by nearby flankers, and will occur when there is overlap between the target and flank (either physically, or in the same neural unit) that obscures the distinguishing feature(s) used for letter identification. Previous studies (Levi, Klein, & Hariharan, 2002; Hariharan et al., 2005) using Gaussian and Gabor stimuli showed that foveal contour interaction is essentially pattern masking.

Siderov et al. suggest that center-to-center separation may be a more appropriate metric when the flanking targets do not have well defined edges (as was the case for Levi, Klein, & Hariharan, 2002; Hariharan et al., 2005). However, regardless of the definition, it is clear that when convolved with the eye’s point spread function, letters and flanking bars at edge-to-edge separations of 0.5 and 1.0 bar widths overlap. A computational simulation of this simple optical form of lateral masking is provided in Appendix A (in Supplemental material).

Siderov et al. expressed the flanker-to-target distance in terms of the edge-to-edge separation, based on the work of Takahashi (1968). However, there are several issues with this: (i) With blurred stimuli (such as Gaussian or Gabor targets and flankers) it is not possible to accurately specify the edge-to-edge separation without making assumptions. (ii) The stimuli Takahashi employed were quite idiosyncratic, comprising a tiny line target with subject-controlled width (defining the threshold using the method of adjustment), surrounded by flanking lines. It is not obvious that her task, which could be interpreted as contrast detection, can be extended to more straightforward acuity tasks such as letter identification. iii) It is clear from the literature that edge-to-edge angular spacing (used initially by Bouma, 1970) is probably not appropriate for peripheral vision. Using this measure, changing the target size would make the center-to-center critical spacing change accordingly, however, multiple studies have shown that in the periphery the center-to-center critical spacing is more or less independent of target size (Levi & Carney, 2009, 2011; Pelli & Tillman, 2008; Pelli, Palomares, & Majaj, 2004; Strasburger, Harvey, & Rentschler, 1991; Tripathy & Cavanagh, 2002), although this independence is not perfect (Gurnsey, Roddy, & Chanab, 2011; see also Pelli, Palomares, & Majaj, 2004, Fig. 5b and Levi, Hariharan, & Klein, 2002). Indeed, Levi and Carney (2009) showed that in peripheral vision, increasing the width of the flanker while keeping its inner edge fixed results in reduced crowding. Thus, if the proposal of Siderov, et al. is correct (the edge-to-edge critical spacing is a fixed angular subtense for foveal targets) it is evidence that foveal contour interaction is quite different from peripheral vision.

One important difficulty in Siderov et al’s study, and thus, in our re-analysis of their data, is that the variable “contrast” and “size” are confounded. Siderov et al. emphasize the dependencies on contrast (and tolerate the fact that size co-varies), while we emphasize the dependencies on size (which are confounded by contrast variations). As stated previously, the extent of crowding is thought to be independent of both of these variables (Pelli, Palomares, & Majaj, 2004; Tripathy & Cavanagh, 2002; and references above), but nearly all studies have co-varied the two, either directly, to maintain the same unflanked performance (as in Siderov et al., 2013 and Tripathy and Cavanagh (2002)) or indirectly, by measurement of contrast thresholds. A recent study suggests that at low contrasts (<10% Weber) critical spacing increases slightly even when the size is increased accordingly (Coates, Chin, & Chung, 2013). However, for most pairs of contrast and size, the critical spacing does appear to be independent of these two variables when in a reasonable regime (i.e., within 80–95% correct when unflanked), but more systematic experiments are necessary.

In summary, we believe the interesting trends shown in the data of Siderov et al. are compatible with a two-mechanism model in which crowding is a small fixed angular extent for small targets, and is proportional to target size for larger, low contrast targets. Indeed, Song, Levi, and Pelli (submitted for publication) suggest that the legibility of a flanked letter can be well accounted for by a model that posits size and spacing limits due to acuity, overlap masking (which is target size dependent), and crowding (which is target size independent). In this model, in normal foveal, peripheral and amblyopic vision, a letter is only legible if it respects all three limits.

Supplementary Material

Appendix

Acknowledgments

Supported by a Grant (RO1 EY01728) from the National Eye Institute, NIH, Bethesda, MD. We thank the anonymous reviewers for their thoughtful comments and suggestions.

Appendix A. Supplementary material

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.visres.2013.10.016.

Contributor Information

Daniel R. Coates, Vision Science Graduate Program, University of California at Berkeley, Berkeley, CA 94720-2020, USA

Dennis M. Levi, School of Optometry and Helen Wills Neuroscience Institute, University of California at Berkeley, Berkeley, CA, USA.

References

  1. Andriessen JJ, Bouma H. Eccentric vision: Adverse interactions between line segments. Vision Research. 1976;16:71–78. doi: 10.1016/0042-6989(76)90078-x. [DOI] [PubMed] [Google Scholar]
  2. Bedell HE, Siderov J, Waugh SJ, Zemanová R, Pluháček F, Musilová L. Contour interaction for foveal acuity targets at different luminances. Vision Research. 2013;89:90–95. doi: 10.1016/j.visres.2013.07.009. http://dx.doi.org/10.1016/j.visres.2013.07.009 (August 30) [DOI] [PubMed] [Google Scholar]
  3. Bouma H. Interaction effects in parafoveal letter recognition. Nature. 1970;226:177–178. doi: 10.1038/226177a0. [DOI] [PubMed] [Google Scholar]
  4. Coates DR, Chin JM, Chung STL. Factors affecting crowded acuity: Eccentricity and contrast. Optometry and Vision Science. 2013;90:628–637. doi: 10.1097/OPX.0b013e31829908a4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Danilova MV, Bondarko VM. Foveal contour interactions and crowding effects at the resolution limit of the visual system. Journal of Vision. 2007;7(2):25, 1–18. doi: 10.1167/7.2.25. http://dx.doi.org/10.1167/7.2.25. < http://journalofvision.org/ 7/2/25/>. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ehrt O, Hess RF. Foveal contour interaction: Detection and discrimination. Journal of the Optical Society of America A: Optics, Image Science, and Vision. 2005;22:209–216. doi: 10.1364/josaa.22.000209. [DOI] [PubMed] [Google Scholar]
  7. Flom MC, Weymouth FW, Kahneman D. Visual resolution and contour interaction. Journal of Optical Society of America. 1963;53:1026–1032. doi: 10.1364/josa.53.001026. [DOI] [PubMed] [Google Scholar]
  8. Gurnsey R, Roddy G, Chanab W. Crowding is size and eccentricity dependent. Journal of Vision. 2011 Jun 17;11(7):15. doi: 10.1167/11.7.15. [DOI] [PubMed] [Google Scholar]
  9. Hess RF, Dakin SC, Kapoor N. The foveal ‘crowding’ effect: Physics or physiology? Vision Research. 2000;40:365–370. doi: 10.1016/s0042-6989(99)00193-5. [DOI] [PubMed] [Google Scholar]
  10. Latham K, Whitaker D. Relative roles of resolution and spatial interference in foveal and peripheral vision. Ophthalmic and Physiological Optics. 1996;16(1):49–57. [PubMed] [Google Scholar]
  11. Levi DM. Crowding – An essential bottleneck for object recognition: A mini-review. Vision Research. 2008;48:635–654. doi: 10.1016/j.visres.2007.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Levi DM, Carney T. Crowding in peripheral vision: Why bigger is better. Current Biology. 2009;19:1988–1993. doi: 10.1016/j.cub.2009.09.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Levi DM, Carney T. The effect of flankers on three tasks in central, peripheral and amblyopic vision. Journal of Vision. 2011;11(1):10. doi: 10.1167/11.1.10. http://dx.doi.org/10.1167/11.1.10 (January 10) [DOI] [PubMed] [Google Scholar]
  14. Levi DM, Hariharan S, Klein SA. Suppressive and facilitatory spatial interactions in peripheral vision: Peripheral crowding is neither size invariant nor simple contrast masking. Journal of Vision. 2002;2(2):167–177. doi: 10.1167/2.2.3. [DOI] [PubMed] [Google Scholar]
  15. Levi DM, Klein SA, Aitsebaomo AP. Vernier acuity, crowding and cortical magnification. Vision Research. 1985;25:963–977. doi: 10.1016/0042-6989(85)90207-x. [DOI] [PubMed] [Google Scholar]
  16. Levi DM, Klein SA, Hariharan S. Suppressive and facilitatory spatial interactions in foveal vision: Foveal crowding is simple contrast masking. Journal of Vision. 2002;2:140–166. doi: 10.1167/2.2.2. [DOI] [PubMed] [Google Scholar]
  17. Pelli DG, Palomares M, Majaj NJ. Crowding is unlike ordinary masking: Distinguishing feature integration from detection. Journal of Vision. 2004;4:1136–1169. doi: 10.1167/4.12.12. [DOI] [PubMed] [Google Scholar]
  18. Pelli DG, Tillman KA. The uncrowded window of object recognition. Nature Neuroscience. 2008;11:1129–1135. doi: 10.1038/nn.2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Siderov J, Waugh SJ, Bedell HE. Foveal contour interaction for low contrast acuity targets. Vision Research. 2013;77:10–13. doi: 10.1016/j.visres.2012.11.008. http://dx.doi.org/10.1016/j.visres.2012.11.008 (January 25) [DOI] [PubMed] [Google Scholar]
  20. Song S, Levi DM, Pelli DG. Size and spacing limit letter identification, with promise of improved visual screening for amblyopia submitted for publication. [Google Scholar]
  21. Strasburger H, Harvey LO, Rentschler I. Contrast thresholds for identification of numeric characters in direct and eccentric view. Perception & Psychophysics. 1991;49:495–508. doi: 10.3758/bf03212183. [DOI] [PubMed] [Google Scholar]
  22. Takahashi ES. PhD Thesis. School of Optometry; U. C. Berkeley: 1968. Effects of flanking contours on visual resolution at foveal and near-foveal loci. [Google Scholar]
  23. Toet A, Levi DM. The two-dimensional shape of spatial interaction zones in the parafovea. Vision Research. 1992;32:1349–1357. doi: 10.1016/0042-6989(92)90227-a. [DOI] [PubMed] [Google Scholar]
  24. Tripathy SP, Cavanagh P. The extent of crowding in peripheral vision does not scale with target size. Vision Research. 2002;42:2357–2369. doi: 10.1016/s0042-6989(02)00197-9. [DOI] [PubMed] [Google Scholar]
  25. Westheimer G, Hauske G. Temporal and spatial interference with vernier acuity. Vision Research. 1975;15:1137–1141. doi: 10.1016/0042-6989(75)90012-7. [DOI] [PubMed] [Google Scholar]
  26. Whitney D, Levi DM. Visual crowding: A fundamental limit on conscious perception and object recognition. Trends in Cognitive Sciences. 2011;15:160–168. doi: 10.1016/j.tics.2011.02.005. http://dx.doi.org/10.1016/j.tics.2011.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Appendix
NIHMS882433-supplement-Appendix.pdf (219.5KB, pdf)

RESOURCES