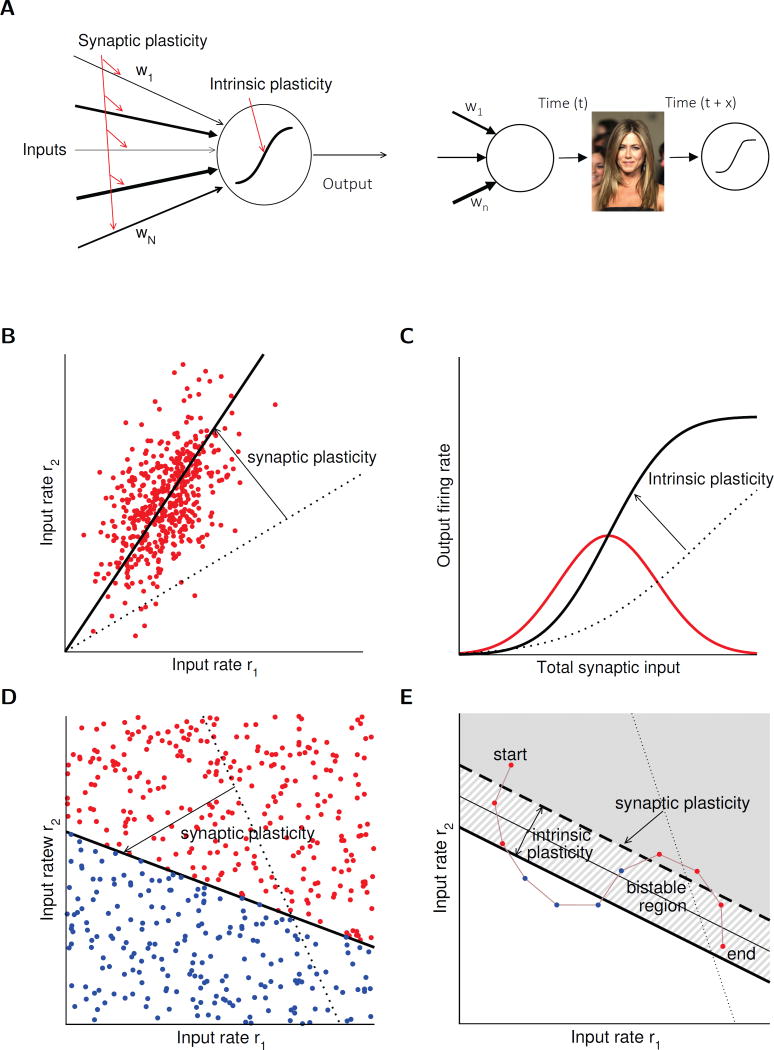
Figure 4.

Theoretical models of intrinsic and synaptic plasticity. (A) Left: Sketch of a simplified single neuron model showing synaptic weight adjustment by synaptic plasticity. Synaptic input weights are summed linearly and passed through a static non-linearity. Loci of plasticity are indicated in red. Right: Illustration of the hypothesis that the adjustment of synaptic weights (synaptic input map) and the plasticity of the intrinsic amplification factor can be separated in time. The example shown here depicts a face-recognition cell encoding the face of the actress Jennifer Aniston. In such highly specialized ‘concept cells’ synaptic input weights are optimally adjusted so that the neuron encodes the object, or a generalized concept of it. Intrinsic plasticity – occurring at time t+x – may enhance engram representation without altering synaptic weight ratios, but based on pre-existing connectivity. Image copyright: the authors (Editorial use license purchased from Shutterstock, Inc.). (B) – (C) Unsupervised learning. (B) Classic unsupervised synaptic plasticity rules allow a neuron to pick the direction of maximal variance in its inputs. Red dots show inputs drawn from a correlated 2D Gaussian distribution, in the space of two inputs to a neuron. The dotted line shows the initial synaptic weight vector. The total synaptic input to a neuron is given by the dot product between the input vector and the synaptic weight vector. Classic Hebbian synaptic plasticity rules – such as the Oja rule – adjust the weight vector until it picks the direction of maximal variance in the inputs, therefore performing principal component analysis (PCA). (C) The resulting distribution of total synaptic inputs is shown in red. The dotted line shows an initial static transfer function (f-I curve) that maximizes mutual information between neuron output and input. It is proportional to the cumulative distribution function of the inputs (Laughlin, 1981). Intrinsic plasticity could adjust this non-linearity until the transfer function matches the optimal one. (D) – (E) Supervised learning. (D) A classic supervised learning problem: the neuron should separate inputs into two classes (red: neuron should be active; blue: neuron should be inactive). The neuron learns to classify inputs by changing its synapses (modifying the hyperplane that separates active and inactive regions). Intrinsic plasticity can help by adjusting the neuronal threshold that measures the distance of the hyperplane from the origin. Learning can be achieved using the classic perceptron algorithm. (E) In some cases, a standard perceptron algorithm fails. In the example shown here, the neuron should learn a particular sequence of input-output associations (shown by colored dots connected by brown line). The neuron should be active in response to red inputs, but inactive for blue inputs. This example cannot be learned by a standard perceptron, because no straight line separating the blue and red dots exists. However, a bistable neuron can learn this sequence: in the bistable region (hatched region between the two thick black lines) the state of the neuron depends on the initial condition. It is active when it starts from an active state (gray shaded region), and inactive when it starts from an inactive state (white region). Intrinsic plasticity could in principle allow a neuron to become bistable and therefore allow it to solve problems that are not learnable by standard perceptrons (Clopath et al., 2013).