Abstract
Experiments have suggested that ion correlation and fluctuation effects can be potentially important for multivalent ions in RNA folding. However, most existing computational methods for the ion electrostatics in RNA folding tend to ignore these effects. The previously reported Tightly Bound Ion (TBI) model can treat ion correlation and fluctuation but its applicability to biologically important RNAs is severely limited by the low computational efficiency. Here, based on Monte Carlo sampling for the many-body ion distribution, we develop a new computational model, Monte Carlo Tightly Bound Ion (MCTBI) model, for ion binding properties around an RNA. Due to an enhanced sampling algorithm for ion distribution, the model leads to significant improvement in computational efficiency. For example, for a 160-nt RNA, the model causes more than 10-fold increase in the computational efficiency, and the improvement in computational efficiency is more pronounced for larger systems. Furthermore, unlike the earlier model, which describes ion distribution using the number of bound ions around each nucleotide, the current MCTBI model is based on the three-dimensional coordinates of the ions. The higher efficiency of the model allows us to treat the ion effects for medium to large RNA molecules, RNA-ligand complexes, and RNA-protein complexes. This new model, together with proper RNA conformational sampling and energetics model, may serve as a starting point for further development for the ion effects in RNA folding and conformational changes and for large nucleic acids systems.
Keywords: ion-nucleic acid interaction, Tightly Bound Ion theory, RNA folding, ion binding
1 INTRODUCTION
In order to form a folded three-dimensional structure, nucleic acids (RNAs and DNAs) require metal ion binding to neutralize/screen the backbone charges.1–3 Quantitative models for ion-nucleic acids binding would directly impact our ability to predict nucleic acids structures and folding stabilities.4–22 For example, one of the key issues in RNA structure prediction,23–27 is lack of an accurate and efficient method to evaluate the ion effects at various solution conditions, especially for solutions with divalent ions such as Mg2+ ions.
According to the different ways of ion binding to RNA, we can classify bound ions into the different types, such as site-specific bound (or chelated) ions28 and diffuse ions.29 In one extreme, site-specific bound ions are trapped in the specific sites on RNA and are usually fully or partially dehydrated.30 The specific binding is a result of the competition between the gain in ion-RNA attraction and penalty of removing water molecules from ions. Molecular dynamics (MD) simulations have provided deep insights into the atomic details for site-binding processes, such as the site-specific ion binding to a RNA kiss loop,31 the 5S rRNA loop E motif,32 SAM-I riboswitch,33 and many other systems.34–37 In the other extreme, diffuse ions usually remain hydrated and diffuse around the RNA surface. The large number of diffuse ions may dominate the electrostatic contribution to RNA folding stability.38 The classical Counterion Condensation (CC) theory39 and (nonlinear) Poisson-Boltzmann (NLPB) theory40–45 have been widely used to compute the non-specific ion binding thermodynamics. In particular, previous studies showed that the NLPB-predicted ion effects for the diffuse ions were consistent with the results from MD simulations for simple RNA structures.46–49
For a compact tertiary structure of RNA, a significant charge buildup results in a high local counterion concentration around the RNA.49 The high local concentration of the ions would cause strong mutual interference due to volume exclusion and Coulombic interaction. These counterions cannot move “freely” like the diffuse ions. Instead, their distribution is subject to the coupling (correlation) effect and such an effect is more pronounced for multivalent ions,14, 50–53 due to the higher charge. The importance of such an ion correlation effect in RNA folding has been revealed and highlighted in terms of two length scales by Koculi et al.53 Furthermore, ion accumulation around the phosphate groups for tertiary motifs has been found to play an important role in the conformational transition from a compact but non-functional structure to the native functional structure.22 We note that ion correlation may become an important effect for such ion accumulation. For strongly correlated ions, the electric field on an ion is not only a function of the position of the ion but also of the positions of the other ions, especially the nearby ions. Therefore, it is necessary to consider the positions of many ions simultaneously and correspondingly, the ensemble of discrete many-ion distributions. Ion correlation and fluctuation lead to several important properties of ion binding. For example, due to the ion correlation, the binding of the different ions to RNA can be coupled between each other. Such correlated ion binding events can play a more important role in a more compact structure, which is usually formed in the later stage of RNA folding after the formation of the secondary structures. Furthermore, the cooperative/anti-cooperative effects of ion binding may be coupled to a possible correlation-induced enhancement of folding stability and cooperativity.15
Counterion Condensation (CC) and Poisson-Boltzmann (NLPB) both neglect the fluctuation of ion distributions and ion-ion correlations. Experimental results suggest that neglecting these effects for multivalent ions, such as Mg2+ ions, may be responsible for the inaccuracy in the theoretical predictions.50, 54 Several new theories have been developed to treat the ion correlation effect for biomolecular systems.55–58 For example, novel Monte Carlo and coarse-grained molecular dynamics simulations were employed to sample counterion distributions around an RNA,9, 55 and in the three-dimensional interaction site model (3D-RISM), Ornstein and Zernike integral equation theory was used to account for the ion-ion correlations57. In a recently developed model, a generalized counterion condensation theory was developed to explicitly treat Mg2+ ions and ion-ion correlations.58 Tests against experimental data indicate that these models are quite promising. Molecular dynamics (MD) simulations can take into account the ion correlation and fluctuation effects, however, the simulation often requires exceedingly long computer time.46
Motivated by the need to take into account both the ion fluctuation and ion correlation effects, we developed the Tightly Bound Ion (TBI) model.59 The basic approach of the model is to classify ions according to the correlation strength and then treat strongly and weakly correlated ions separately. Multivalent ions such as Mg2+ ions in the close vicinity of the RNA are more likely strongly correlated while other ions, such as those far away from the RNA, are usually weakly correlated. For the strongly correlated ions, the TBI model use an explicit enumeration to sample the (many-body) ion distributions while for the weakly correlated ions, the model employs the mean-field (NLPB) approximation. In the TBI model, we assume ions, including the strongly correlated ions, are hydrated. Extensive comparisons between TBI predictions and experimental results support the conclusion that the TBI model offers improved predictions for ion binding properties and ion-mediated nucleic acids stability for simple helices, pseudoknots, kissing complexes, and more complex tertiary folds.54, 59–65 Since the major difference between the TBI model and the NLPB is the inclusion of the ion correlation effect, a comparison between the TBI and NLPB predictions can may show the contribution from the correlation. Indeed, extensive TBI-NLPB comparisons have been made and the theoretical predictions have been tested against experimental data for the number of excess bound ions10, 14 and the ion-dependence of the free energies.80 The results pointed to possible importance to consider the correlation effect for a variety of RNA structures in multivalent ion such as Mg2+ ion solutions.54, 59–65
However, the TBI model is severely limited by its low computational efficiency. Because the TBI model is based on the time-consuming explicit enumeration of ion distributions, applications of the model to medium (100–200 nts) or large RNA structures (> 200 nts) are not practical. Furthermore, the model, which is based on a coarse-grained description for ion distributions, cannot treat the spatial coordinates of the ions, thus cannot give high-resolution ion distributions. Here we develop a new model (“MCTBI” model) that can treat medium to large RNA structures with high resolution ion distributions. In this paper, we test the validity of the model through extensive theory-experiment comparisons. Furthermore, we demonstrate that the MCTBI model, unlike the previous models, can predict the most probable and the average ion distributions with high resolutions. This model may sever as a solid step toward ultimate goal of accurate prediction for ion-dependent structure and stability for large RNAs.
2 Model development
2.1 TBI model
For a given structure of RNA, we run the NLPB calculation to estimate the ion concentration around the RNA. According to the ion concentration, we compute the ion correlation strength and classify the space into two regions occupied with two types of ions respectively: (a) ions of strong correlation are called the tightly bound (TB) ions and the corresponding spatial region is called the TB region, (b) ions of weak correlation are called diffusely bound (DB) ions and the corresponding region is called the DB region.59 For the DB ions, we apply the NLPB. For the TB ions, we consider correlation and fluctuation through explicit enumeration of the many-body ion distributions. We divide the TB region into cells (TB cells), each around a phosphate, and define a TB ion distribution in terms of the number of ions in each TB cell.
Motivated by the need to overcome the two aforementioned severe limitations of the TBI model, here we develop a new, computationally efficient model. As illustrated below, the new model, Monte Carlo Tightly Bound Ion model (MCTBI), is based on coordinate-based ion distribution and Monte Carlos (MC) sampling for the TB ion distributions. With significantly higher computational efficiency, the MCTBI model can predict the three-dimensional ion distributions and provide ion binding properties. The MCTBI model allows us to treat ion correlation and fluctuation effects for medium to large RNA structures.
2.2 The MCTBI model
The MCTBI model is based on all-atom RNA structures that are either constructed from the X3DNA66 or from the Protein Data Bank.67 As a coarse-grained charge model, each phosphate is assumed to carry an electronic charge −e and other atoms are assumed to be neutral. The RNA is located in a large solution box, whose size is larger than six times of the Debye length in order to reduce the boundary effect.59 The mixed salt solution in the box can contain divalent cationsMg2+, monovalent cations K+ (or Na+), and monovalent anions Cl−. Their bulk concentrations , and satisfy the charge neutrality condition: . Ions are considered as fully hydrated in our study. The (hydrated) ionic radii are rMg2+ = 4.5Å, rK+ = 4.0Å, rNa+ = 3.5Å, and rCl− = 4.0Å, respectively.62, 63
To determine the tightly bound region, we first run the NLPB calculation with the three-step focusing process68, with respective grid sizes 1.7Å, 0.85Å, and 0.425Å. The NLPB solution provides a rough estimation for the spatial distribution of the ion concentration and ion correlation strength.59 The demarcation between the TB region and DB region is established according to the correlation strength. The details of how to separated the two regions have been reported in previous studies.59, 60 In general, a high (bulk) ion concentration leads to a large TB region. Moreover, multivalent ions involve have stronger Coulomb interactions thus have higher tendency to form strong correlation. In contrast, monovalent ions usually have negligible correlation. Therefore, we treat monovalent ions as diffuse ions and according to the correlation strength, classify multivalent ions such asMg2+ ions into TB ions (in the TB region) and DB ions (in the DB region). In general, the TB region is a thin layer of width from zero to a few Angstroms, depending on ion concentration and RNA structure.
For an RNA with N phosphates, we assume that Nb, the number of Mg2+ ions in the TB region, varies from 0 to N. An increasing Nb and the stronger charge neutralization of RNA would cause a weaker ion binding around RNA and a weaker ion correlation. As a result, the actual TB region would be smaller than the one originally determined without considering the TB ions (Nb = 0). We use a fixed TB region in order to enhance the computational efficiency. Because unlike the DB ions, the TB ions are treated more accurately with the full considerations of the discrete distributions and the related correlation and fluctuation, a larger TB region may provide a more reliable description for the ions than a smaller one. Therefore, our use of the fixed TB region may be valid. Furthermore, our previous tests have shown that the predicted results are not very sensitive to small variations of the TB boundary.54, 59–65 As a result, the partition function of the whole system can be calculated as the sum over all the possible Nb’s:
| (1) |
where Nd = N2+ − Nb is the number of the divalent ions in the DB region with N2+ as the total number of the divalent ions in the system. Since the system is divided into two regions, the partition function for a given set of Nb and Nd can be approximately given by
| (2) |
where Zb and Zd are the partition functions of the TB ions and of the DB ions, respectively. In our calculation, we first compute the TB ion partition function Zb(Nb) for the different numbers of TB ions (Nb). For each Nb, we also calculate the DB ion partition function Zd(Nd).
For the (correlation-free) DB ions, the partition function can be calculated as an ideal gas in a mean field:
| (3) |
Here Vd is volume of DB region. N1+ and N− are the number of monovalent cations and anions, kB is the Boltzmann constant and T is the temperature. The factorial terms represent that the ions are identical particles. λ2+, λ1+, and λ− are the thermal wavelengths of the corresponding ions. The free energy ΔGd of the DB ions is the sum of the entropic free energy of the diffuse ions,59 the electrostatic energy, including the (average) electrostatics interaction energy between TB ions and DB ions. ΔGd can be calculated from the effective single-particle ion distribution solved from NLPB:69, 70
| (4) |
Here α denotes the ion species. zαe is the charge of ion species α, ψ(r) and ψ′(r) are the electric potentials at position r with and without the DB ions in the solution, and cα(r) and represent the local (at r) and bulk concentrations, respectively. In this paper, we use kBT as the unit of energy.
We note that ψ(r) − ψ′(r) effectively gives the electric potential due to the charged particles in the TB region. Therefore, the first integral in Eq. 4 is the free energy for the interaction between the DB ions and the charged particles in the TB region plus the enthalpic part of the free energy for the DB ions.70 The second integral gives the entropic part of free energy for the DB ions.
In the calculation, for each Nb (the number of the TB ions), we sample the TB ion distributions. Based on the interaction energy for the particles in the TB region, we compute the statistical weight, the mean free energy for the TB ions, and the Boltzmann-averaged mean TB ion distribution. We note that such a mean TB ion distribution is determined from the interactions inside the TB region only and does not include interactions with the DB ions.
The influence of the DB (TB) ions on the TB (DB) ions is treated with an approximation. Fore each given Nb, the above ψ(r), ψ′(r) and cα(r) for the DB ions in Eq. 4 are solved from NLPB based on the above mean TB ion distribution (instead of each single discrete TB ion distribution). Such an approximation has the advantage of enhancing the computationally efficiency of the model: For a given Nb, instead of solving NLPB for each of the (large number) discrete TB ion distributions, we only need to solve NLPB once for each mean TB ion distribution. The approximation may be valid because the TB ion distributions are dominated by the interactions with the charges in the TB regions instead of the DB ions. Our previous extensive theory-experiment tests further support the reliability of this approach.54, 59–65
For the TB ions, ion correlation requires the use of the many-body ion distribution instead of a single-particle distribution. The partition function Zb of a Nb-ion system is given by
| (5) |
and the statistical weight W(Nb) involves the configurational integral for all the Nb ions:
| (6) |
Here we use Ri (i ∈ [1,Nb]) to represent the coordinates of the ion i in the TB region and ΔGb is the interaction energy between all the charged particles inside the TB region, including volume exclusion, Coulombic interaction and dielectric polarization energies. Here the charges inside the TB region include not only the TB ions but also the phosphates. In our calculation, the excluded volume effect is modeled by a Lennard-Jones (LJ) potential and the polarization energy is computed from the Generalized Born (GB) model:
| (7) |
The first term in the equation above is the Coulombic energy between the charges in the TB region. Zi(or j)e in the above equation is the charge of particle i(or j), εR (= 20 in our calculation) is the dielectric constant of RNA, and rij is the distance between particles i and j. The second term is the LJ potential with uo(= 0.35) as the LJ constant and σij as the equilibrium distance between particles i and j. Here we set σij as the addition of the radius of the two particles. The third term above is the mutual polarization energy induced by other charges, εW(= 78) is the dielectric constant of water and Bi(or j) is the Born radius for particle i(or j). The forth and fifth terms represent the self-polarization energies of phosphates (subscript P) and ions (subscript I).
Combining Eqs. 2, 3, and 5 together results in the following partition function for a given set of (Nb,Nd):
| (8) |
Here
| (9) |
is the partition function of the ideal solution without the insertion of RNA. Since the number of the multivalent ions in the whole system is much larger than that in the TBI region (N2+ ≫ Nb), we have , and Eq. (8) becomes
| (10) |
From the equations above, the key to the calculation of the partition function is to evaluate the statistical weight W(Nb) for a given Nb. In this paper, we develop a Monte Carlo-based method for W(Nb).
2.3 Lattice Model of the TB region
We use a simple cubic lattice with adaptive lattice size to configure ion distribution. For a low bulk concentration of the multivalent ions, we choose a grid (lattice) size lb = 0.425Å (= the final grid size in the aforementioned three-step focusing process for the NLPB calculation for the DB region). For a high ion bulk concentration, there are usually more ions bound in the TB region the sampling of the ion distributions could be time-consuming. To enhance the computational efficiency, we choose lb such that the number of lattice sites Ns inside the TB region is ≈ 100 × N. The TB ions are configured on the lattice sites such that each site can be occupied by at most one ion. As a result, there are possible ways to partition Nb TB ions onto Ns sites. In other words, W(Nb) in Eqs. 5 and 6 involves different spatial configurations for the TB ions.
Following the Rosenbluth-Rosenbluth (RR) method,77 the statistical weight W(Nb)/Nb! for the Nb particles in a discrete space can be calculated through a process of adding particles one by one:
| (11) |
where the product corresponds to the process of adding 1, 2, …, Nb ions.
Consider the step of inserting the i-th ion into the system of the pre-existing i−1 ions and N phosphate charges. The statistical weight of the i-th ion w(i) is given by
| (12) |
In the above equation, mi denotes the number of the available (vacant) sites for placing the ith ion, given the constraint that (i − 1) ions have already occupied their respective sites through the preceding steps. The factor w(i)/i is the change in the statistical weight caused by the insertion of the ith ion. ΔUi(k) denotes the interaction energy between the newly inserted ith ion (at the grid site k) and the pre-existing (i − 1) ions and all the N phosphate charges. ΔUp is the energy (LJ potential, Coulombic energy, and the polarization energy) between the phosphate charges. Since ΔUp is independent of the ion distribution, we can separate it out from ΔUi(k).
Following Eq. 7, ΔUi(k) can be computed using the following formula
| (13) |
In a (hypothetical) ideal situation, if all the particles in the TB region are electrically neutral, then ΔUi(k) = ΔUp = 0 and Eq. 11 gives , the number of ways to configure Nb ions on the Ns lattice sites. Moreover, Eq. 12 shows , which represents the available volume for placing the i-th ion.
When a new ion is inserted, the interaction between the newly added ion and the pre-existing ions would perturb the distribution of the pre-existing ions. Such a backtrack effect is ignored in the original RR algorithm.77 To account for the backtrack effect, we need to adjust ion distributions on the fly as we insert ions.78
Different methods can be used to treat the backtrack effect. We may use the conventional Monte Carlo simulation to sample the low energy distributions. For example, we can use Metropolis algorithm to randomly select and move the ions. However, due to the ruggedness of the energy landscape, such a simple algorithm would be impractical due to its low efficiency. Here we develop a new sampling algorithm to treat the backtrack issue of the TB ion distributions.
2.4 An importance sampling method
We develop an “insertion-deletion” algorithm for the co-insertion sampling of the ion distribution, i.e., the ion distribution changes with the number of ions in the system. In this approach, we first insert N (the maximum allowed number of TB ions) ions one by one into the TB region, randomly place them in the TB region such that the low-energy sites have higher probabilities to be occupied. We then randomly remove the ions one by one such that ions at higher energy sites are more likely to be removed. As we remove 0, 1, 2, …,N − 3,N − 2,N − 1 ions one by one, we generate low-energy distributions for N,N − 1,N − 2, …, 3, 2, 1-ion systems, respectively. Repeating the above random process multiple times leads to an ensemble of low energy distributions for the different number of ions. Because the ion distributions are generated from the subset of the full N-ion distributions, our insertion-deletion approach accounts for the full ion correlation, including the impact of the later inserted ions on the earlier inserted ions.
Our computation procedure involves the following steps:
-
Forward process: inserting ions. We perform Monte Carlo sampling to generate Mf samples of the N-ion distribution. Specifically, to insert the i-th ion, we enumerate all the available vacant sites k = 1, 2, 3, …mi. For each site k, we calculate the total interaction energy change ΔUi(k) (Eq. 13) if the i-th ion is placed at site k. The probability of placing the i-th at site k is
(14) To sample the ion positions with the above probability, we divide the interval [0, 1] into mi segments, each of length pf (i, k) for k = 1, 2, …,mi: Σk pf (i, k) = 1. We then generate a random number r ∈ [0, 1] to select the site k (if r falls in the k-th segment). This way, sites of lower interaction energy ΔUi(k) would have higher probability to be visited.
-
Backward process: removing ions. For each N-ion distribution generated in the above forward process, we produce an ensemble of Mb sequences for the ions, where each sequence represents the order of ions to be removed from the N-ion distribution. Specifically, to guide the sampling toward the low-energy distributions, we use the following probability function for removing an ion j at position k:
(15) where ΔUj(k) is the total interaction energy between ion j and all the phosphate charges and the remaining ions. The sum is effectively the “partition function” over the ensemble of the ion removal sequences. According to the above probability function, Ions with higher energy ΔUj(k) would have higher probability to be removed.
Updating ion distribution. For a system of s ions (s = 1, 2, …,N), the above procedure provides an ensemble of low-energy distributions as given by the coordinates of the last removed s ions. These ion distributions serve as the updated s-ion distributions in the insertion-deletion process.
Computing . For each generated N-ion distribution in the forward process, we compute the average weight for w(i) in Eq. 12. Here the averaging is over the ensemble of the updated (i − 1)-ion distributions. Eq. 11 gives the statistical weight W(Nb).
Computing . Averaging the W(Nb) over the Mf samples of the N-ion distribution gives the mean statistical weight of the Nb bound ion system.
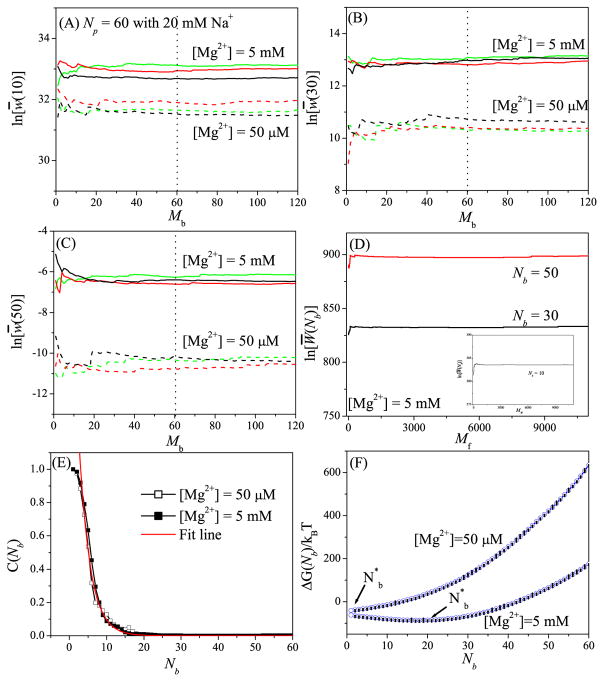
To examine the robustness of the above sampling algorithm, we test the different Mb’s for different RNAs. The results shown in Figs. 1a–d and Figs. S1–S7, suggest that (a) Mb = N may be sufficient for stable results and (b) Mf = Ns (the number of the lattice sites for the TB ions) gives the optimal balance between efficiency and the robustness.
Figure 1.
Test results for the robustness of the Monte Carlo sampling in the “insertion-deletion” algorithm using a 60- nt RNA helix as the test case. (A) i = N/6, (B) i = N/2, and (C) i = 5N/6 show the results for the deletion process. For each of the three different sets (red, black, and green) for the N-ion (N = 60 here) distribution (generated through the insertion process), we run Mb Monte Carlo samples for the deletion process to generate an ensemble of the distributions for the i − 1 ions. Based on the distribution of the i − 1 ions, the statistical weight w(i) for the i-th ion is computed. (D) and the inset in (D) show the results for the Monte Carlo sampling in the insertion process. Here we show the results for Nb = N/6 (inset), Nb = N/2 (black line), and Nb = 5N/6 (red line). (E) Correlation (C(Nb)) between the statistical weights before and after the deletion step. The characteristic correlation-specific TB ion number is found to be 3 for this system. (F) The free energy ΔG(Nb) as a function of Nb. The error bar shows the fluctuation for the different Monte Carlo samples of the TB ion distribution.
It should be noted that although our “insertion-deletion” algorithm and the MC method used in Ref. 55 both have two MC steps to sample the ion distributions, however, the main ideas about the backtrack algorithm are quite different. While the current model uses the “deletion” algorithm to enhance the sampling of the low-energy ion distributions, the MC method in Ref. 55 employs a neighbor cyclic permutation method.
To examine the importance of the deletion part in the model. we calculate the correlation C(Nb) between the statistical weights before and after the deletion procedure:
| (16) |
where Wi(Nb) and denote the statistical weights (Eq. 11) in the i-th Monte Carlo sample for the Nb-TB ion distribution before and after the deletion, respectively. A small C(Nb) indicates a large change in the statistical weight caused by the deletion step, therefore, removing the deletion step could result in the loss of important TB ion distributions. As shown in Fig. 1E and Figs. S1E–S7E, the correlation function decays exponentially with a characteristic for correlation:
| (17) |
Physically, the electrostatic interaction energy and the statistical weigh W(Nb) for a system of larger number of TB ions (larger Nb) are more sensitive to the change of ion distribution, resulting in a weaker correlation. Tests for the different RNA structures (Figs. S1E–S7E) show that is dependent on the RNA structure and less sensitive to the ion concentration.
To investigate the probability distribution of the number of the TB ions (Nb), we calculate the free energy ΔG(Nb)[= −kBT ln(Z(Nb,Nd)] for the different Nb’s; See Figs. 1F and S1F–S7F (with error bars to indicate the fluctuations from the different Monte Carlo samples of the ion distribution). At low [Mg2+], the most probable TB ion number (minimum ΔG(Nb)) is small, while at high [Mg2+], shifts to the larger number Nb end, meaning that more Mg2+ ions are bound tightly to the RNA surface. Furthermore, the figures show that the most probable TB ion number is much larger than for high [Mg2+]. The result provides further support for the necessity to include the deletion step for sampling the TB ion distribution.
3 RESULTS AND DISCUSSION
To test the MCTBI model and investigate the ion binding properties for RNA, we apply the MCTBI model to a variety of RNA structures in different ionic concentrations. Theory-experiment comparisons provide effective tests for the model. Moreover, the model can predict several important properties of ion-RNA interactions. First, the model gives the fraction of the excess bound ions fα per nucleotide for ion species α:
| (18) |
where the partition functions Z(Nb,Nd) and Z in Eq. 18 are determined from Eqs. 1 and 10, respectively, and Γα(Nb) is the number of excess ions, including the TB ions and the excess DB ions:
| (19) |
Second, the MCTBI model can predict the electrostatic free energy ΔG = −kBT ln(Z) and the three-dimensional spatial distribution of the TB ions. The probability of finding a TB ion at position (grid point) k is given by
| (20) |
Here n(Nb, k) is the number of Nb-ion distributions (out of the totally MfMb sampled distributions) with site k occupied by a TB ion.
3.1 Comparisons with the previous models
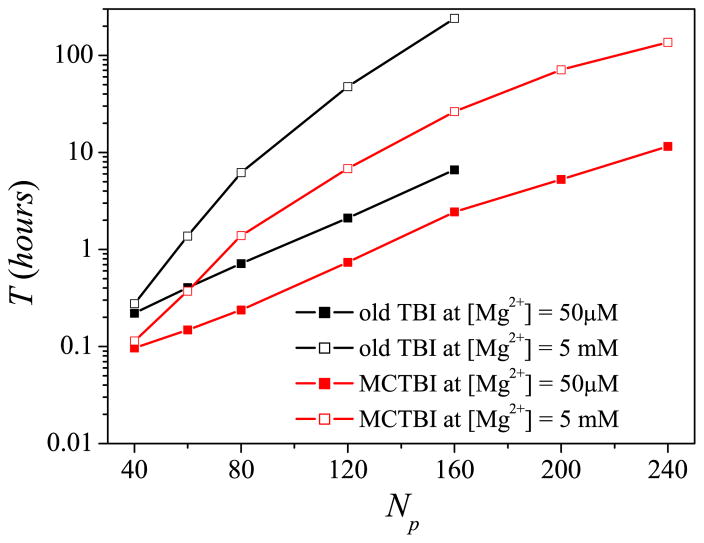
To test the efficiency and accuracy of the MCTBI, we first use a simple RNA duplex of length N = 40 to 240 in a Mg2+ solution as a test system. As shown in Fig. 2, the computational time depends not only on the RNA sequence length N but also on the ion concentration [Mg2+]. Lower ion concentration causes a smaller TB region and a smaller sampling space, therefore, requires a shorter computer time. Comparisons with the original TBI show that the MCTBI model is computationally much more efficient then the existing TBI model. The improvement in computational efficiency is more pronounced for high [Mg2+] and larger RNAs, where MCTBI model is over 10 times more efficient than the existing TBI model (Fig. 2).
Figure 2.
The computer time as a function of the RNA length N for the MCTBI and the previous TBI models64 for various [Mg2+]’s with 20 mM Na+ background. The time is for the computation for the binding fractions, electrostatical free energy, and TB ion spatical distribution. The calculations are performed on a PC with Intel i7- 4790 processor and 16GB RAM.
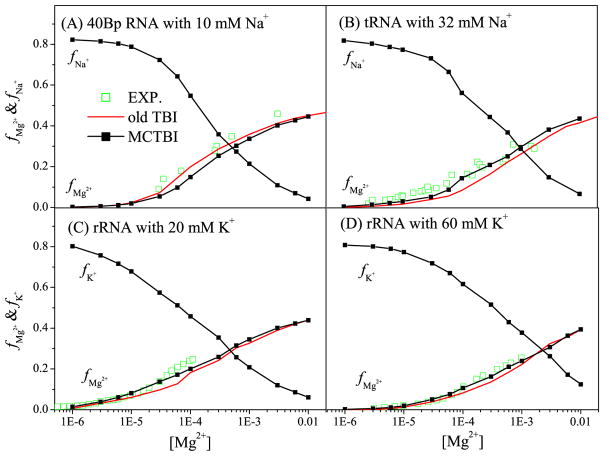
Furthermore, we show the results of the binding fraction fMg2+ as a function of [Mg2+] for the different RNA structures (See Fig. 3). We find that the MCTBI predictions agree with the experimental data and MCTBI gives overall more accurate predictions than the original TBI. As [Mg2+] increases, the entropic cost for ion binding is reduced, causing more Mg2+ ions binding to RNA. Moreover, an increased Mg2+ ion binding would cause reduction in monovalent ion binding, so fNa+(or K+) decreases with increasing [Mg2+]. From the comparisons between the predictions from the MCTBI model and the original TBI model as shown in Figs. 2 and 3, we find that the MCTBI in general can provide more efficient and more accurate predictions for the ion-RNA binding properties.
Figure 3.
The [Mg2+]-dependence of the Mg2+ and Na+ (or K+) binding fractions per nucleotide for four different test systems: 80-nt RNA duplex (A-form helix) with 10mM Na+, 76-nt yeast tRNAPhe (PDB ID: 1TRA79) with 32 mM Na+, and 58-nt fragment of rRNA (PDB ID: 1HC881) with 20 and 60 mM K+, respectively. The experimental data are from the References 82–84, respectively.
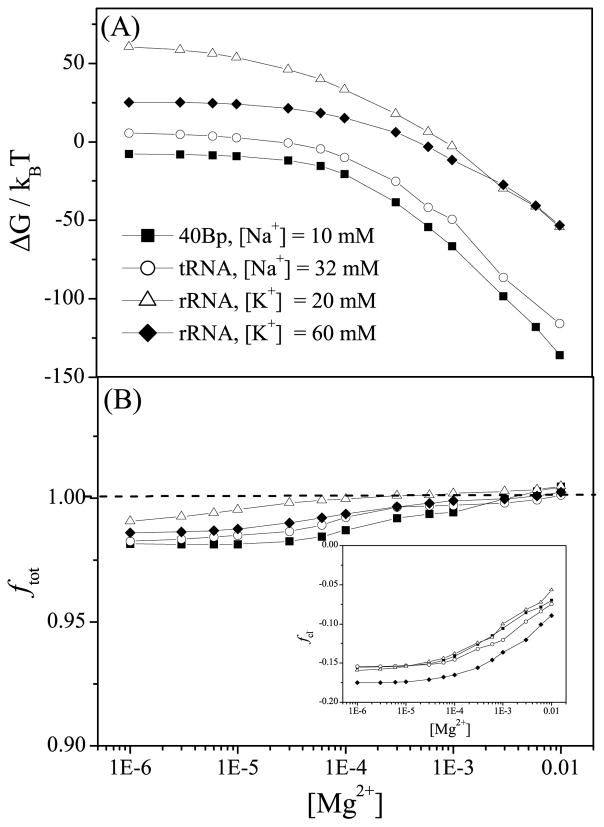
As shown in Fig. 4A, a higher concentration of Mg2+ ions can help lowering the electrostatic free energy of the system. Moreover, for a mixture solution of monovalent and divalent ions, the overall ion binding shows a competition between monovalent and divalent ions. From the plots for the rRNA fragment system at [K+] = 20mM (line with empty triangles) and [K+] = 60mM (line with filled diamonds), we find that in a a dilute [Mg2+] solution, the electrostatic free energy ΔG is dominated by the monovalent ions and is higher for 20 mM [K+] than 60 mM [K+]. For higher [Mg2+] (> 5 mM), the behavior of ΔG is dominated by the Mg2+ ions instead of the K+. As a result, 20 mM [K+] and 60 mM [K+] give nearly the same value for the electrostatic free energy ΔG for the same [Mg2+].
Figure 4.
(a) The electrostatic free energies ΔG and (b) the total charge neutralization ftot as functions of [Mg2+] for the 80-nt RNA duplex with 10 mM Na+, 76-nt yeast tRNAPhe with 32mM Na+, and 58-nt fragment of rRNA with 20 mM and 60 mM K+, respectively. The inset of (b) shows the binding fraction of Cl− ions.
The MCTBI model can also predict the net bound charge (including the anion charges) per nucleotide ftot (see Fig. 4b):
| (21) |
Although fNa+(or K+) decreases with the increase of [Mg2+], the net effect of the increases in fMg2+ and fCl− (see the inset of Fig. 4b) results in the increase in net charge ftot. Since each phosphate group carries −e charge, an ion-dressed RNA at a dilute [Mg2+] (< 1 mM) shows a weak negative charge. At high [Mg2+], the sign of RNA net charge could be reversed (from negative to positive). In addition, in Figs. 3C & D, we find that a higher concentration of monovalent ion can enhance [K+] ion binding to rRNA and dampen [Mg2+] binding. Because the gain in [K+] ion binding makes up the loss of [Mg2+] ion binding, a higher concentration of monovalent ion results in a lower net bound charge ftot.
3.2 Ion-RNA binding properties for Adenine riboswitch
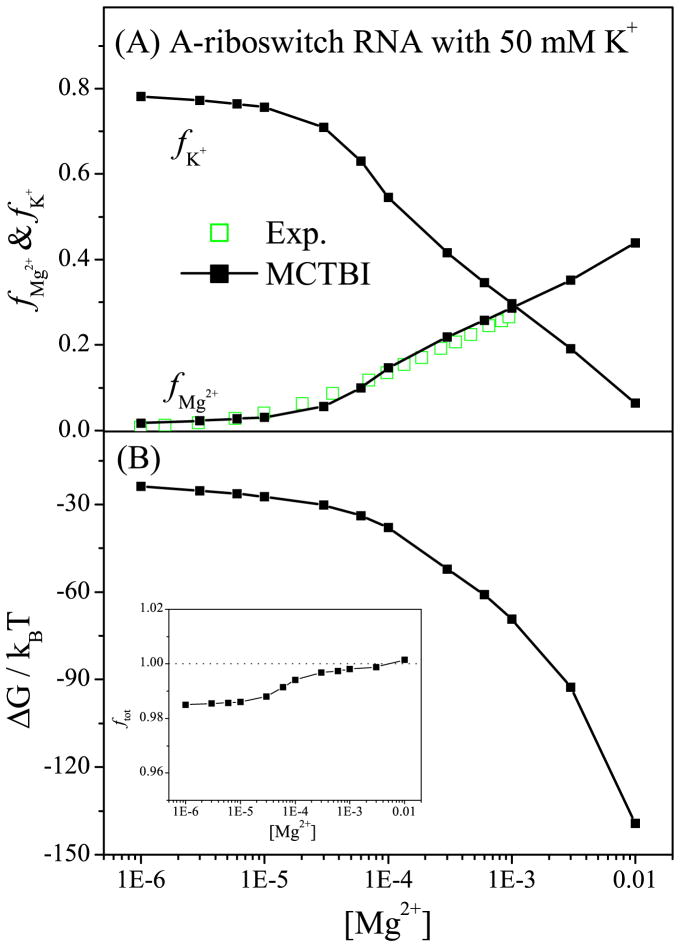
Riboswitches regulate gene expressions for bacteria metabolism. Because of their ion-sensitive structures, riboswitches are excellent systems to study the ion-RNA interactions. Due to the large size of RNA, previous TBI model was unable to treat riboswitches due to the exceedingly long computational time. The significantly improved computational efficiency for the MCTBI model now allows us to treat riboswitches. Here we focus on the 72-nt Adenine riboswitch (A-riboswitch; PDB ID: 1Y2685) with an Adenine ligand To investigate the ion binding properties. Based on the same solution conditions as the one used in the experiment ([K+] = 50mM),86 the MCTBI predictions for the Mg2+ ion binding fraction fMg2+ are in good agreement with the experimental data86 (see Fig. 5a). The model also predicts the decrease in fK+ with the increase of [Mg2+], i.e., the competition between the monovalent and divalent ions. Furthermore, as shown in Fig. 5b, the MCTBI model can predict the electrostatic free energy for the A-riboswitch RNA for a given [Mg2+]. The results suggest that a higher [Mg2+] can help lower the free energy of the ion-riboswitch system.
Figure 5.
Ion binding properties for Adenine riboswitch. (a) The binding fractions of Mg2+ and K+ ions per nucleotide, respectively, and (b) the electrostatic free energy as a function of [Mg2+] with fixed [K+] = 50mM. The inset of (b) shows the fraction of the total charge as a function of [Mg2+].
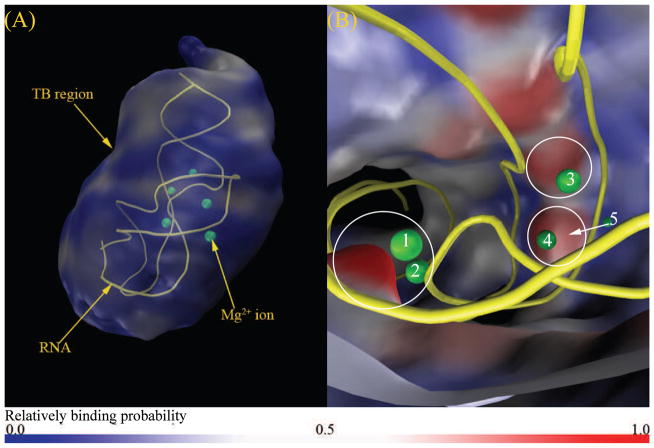
MCTBI can also predict the probability for the ion distributions. Fig. 6 shows the predicted TB Mg2+ ion distribution at [Mg2+] = 2mM and [K+] = 50mM. The result shows two important features of the ion distribution. First, toward the outer boundary of the TBI region, the TB ion concentration decreases and approaches the DB ion concentration. The result is consistent with the classification scheme for the TB and DB regions. Second, the MCTBI model predicts several highly probable ion binding locations. For example, Fig. 6b shows a high-probability ion-binding bulge region around the experimentally observed bound Mg2+ ions labeled as 1 and 2 in the figure. The result supports the notion that there exist discrete “high-probability” locations for ion binding. Ions bound at these locations may become site-specific bound ions observed in the structure determination experiment. In addition to the above sites, the model also predicts high probability regions near the ions labeled 3, 4 and 5 in the figure, respectively.
Figure 6.
Predicted TB Mg2+ ion distribution in a solution with 2 mM Mg2+ and 50 mM K+. (a) and (b) show the “zoom-out” and “zoom-in” views of the Mg2+ ion distribution in the TB region, respectively. The labeled spheres are the bound Mg2+ ions shown in the PDB structure (A-riboswitch, PDB ID: 1Y26, yellow color in the figure).
3.3 Ion binding properties for RNA-protein complexes
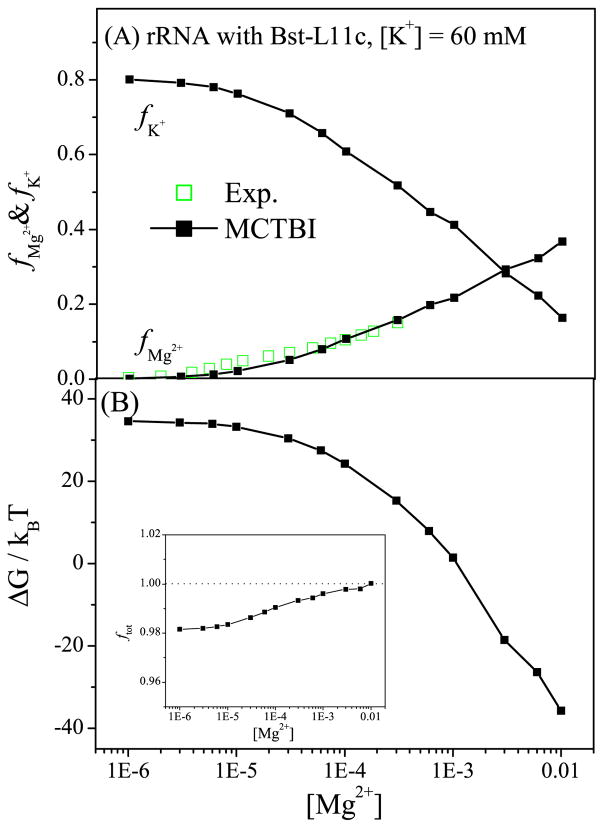
Protein binding is known to influence the ion distribution around RNA and the ion-mediated electrostatic interactions. 87 Given the significantly enhanced computational efficiency and the ability to predict the spatial distributions for ions around RNA, the MCTBI model enables detailed analysis and predictions for the ion effects in RNA-protein complex formation. To test the model and to investigate the ion binding mechanism for RNA-protein complexes, we apply the MCTBI to an experimentally studied 58-nt fragment of rRNA bound with the Bst-L11C protein (PDB ID: 1HC881). Fig. 7 shows the MCTBI-predicted ion binding properties for the complex, such as the fractional numbers fMg2+ and fK+ for bound Mg2+ and K+ ions, respectively, the electrostatic free energy ΔG, and the fractional net charge ftot. The comparison for fMg2+ between the theoretical predictions and the experimental data87 (see Fig. 7a) supports the validity of the MCTBI model.
Figure 7.
The behavior of (a) the binding fractions of Mg2+ and K+ ions per nucleotide and (b) the electrostatic free energy as a function of [Mg2+] with fixed [K+] = 60mM. The inset of (b) shows the fraction of the total charge as a function of [Mg2+]. As an approximation, we use the same dielectric constant for the protein εp and the RNA (εp = εR = 20).
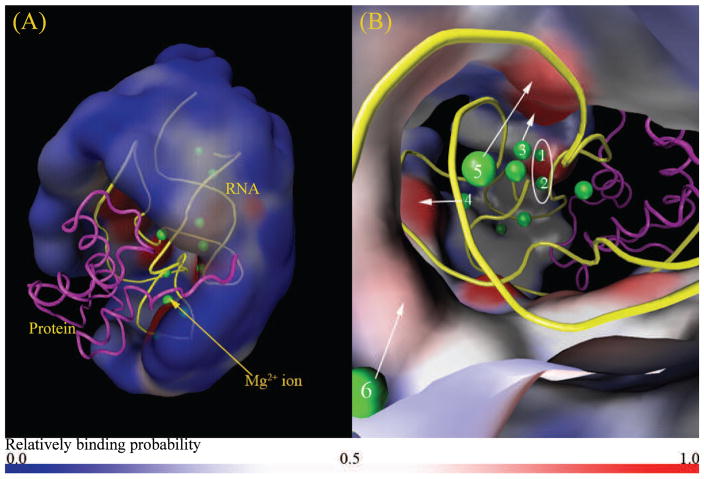
Next we use the MCTBI model to compute the ion distributions, specifically, the TB Mg2+ ion distribution in 60 mM K+ and 2 mM Mg2+. In contrast to the unbound form of RNA (and protein), the RNA-protein complex has a large region in the TB region occupied by the protein (see Fig. 8a). The TB ions are cannot exist in this open region. As shown in Fig. 8a, similar to the the riboswitch system shown in Fig. 6, the probability of finding TB Mg2+ ions near the boundary of the TB region is low, suggesting that ions near the boundary of the TB region approach a weakly correlated DB ion-like state.
Figure 8.
Predicted TB Mg2+ ion distribution in a solution with 2 mM Mg2+ and 60 mM K+. (a) and (b) show the “zoom-out” and “zoom-in” views of the Mg2+ ion distribution in the TB region, respectively. The green spheres are the bound Mg2+ ions shown in the PDB structure (PDB ID: 1HC8) of the RNA (yellow)-protein (magenta). The color code is the same as in Fig. 6.
Furthermore, from the “zoom-in” view shown in Fig. 8b, the MCTBI predicts discrete highly probable positions for bound ions. Some highly probable positions are consistent with the experimentally observed ion binding sites (see ions labeled 1 – 6). Since the current MCTBI model does not treat ion dehydration and chelation effects, the model cannot predict the site-specific bound ions that involve significant dehydration and chelation.
An intriguing experimental finding about the ion binding properties is that at dilute [Mg2+], more Mg2+ ions are bound to the rRNA-protein complex than to the rRNA alone, while at high [Mg2+], the situation is reversed.87 To quantitatively understand this phenomena, as shown in Fig. S8 in the Supplementary Information, we divide the whole space into three parts: the protein region, which is occupied by the protein in the RNA-protein complex and is empty for the unbounded RNA, and the remaining DB and TB regions, which are the DB and TB regions minus the protein region, respectively. We calculate the number of excess bounded Mg2+ ions Γp, Γrtb, and Γrdb in the protein, the remaining TB region, and the remaining DB region, respectively:
| (22) |
Here k, r, r′ and k′ denote the coordinates (grid sites) in the remaining TB region, the remaining DB region, and the protein in the DB and the TB regions, respectively. p(k) (Eq. 20) is the probability of finding a TB ion at position k. Γp, Γrtb, and Γrdb satisfy the following relationship:
| (23) |
where Γtot is the total number of excess ions and N is the number of nucleotides (sequence length). From the MCTBI-predicted results for RNA-protein complex and RNA alone with [Mg2+] = 10μM and 2 mM (see Table 1), respectively, we find the following two competing effects. Compared to the unbound RNA, the presence of the protein in the protein-RNA complex would exclude ion presence in the protein region (Γp = 0). On the other hand, the presence of protein, which has a lower dielectric constant than bulk water, would result in an enhanced ion-RNA attraction. The former and later effects tend to cause an increase and decrease in Γtot, respectively. In the case of dilute [Mg2+], the TB region is so thin that the exclusion effect of protein on TB ions is negligible, as a result, the protein-RNA complex has a larger Γtot than the unbound RNA. However, at high [Mg2+], the volume exclusion from the protein becomes important, thus the protein-RNA complex has a smaller Γtot than an unbound RNA.
Table 1.
The number of excess (bound) ions in the protein region, the remaining TB region, the remaining DB region, and the whole space in a solution with dilute [Mg2+] and high [Mg2+].
| RNA type | Γp | Γrtb | Γrdb | Γtot |
|---|---|---|---|---|
| [Mg2+] = 10μM | ||||
| Unbound RNA | 0.02 | 1.12 | 0.09 | 1.23 |
| RNA complex | 0.00 | 1.26 | 0.09 | 1.35 |
|
| ||||
| [Mg2+] = 2mM | ||||
| Unbound RNA | 3.51 | 15.24 | 1.51 | 19.85 |
| RNA complex | 0.00 | 16.82 | 1.54 | 18.36 |
4 CONCLUSION
By taking into account the correlation and fluctuation effects, the TBI model provides a method for reliable prediction of the ion effects in nucleic acid systems. However, the applicability of the method has been limited by the low computational efficiency due to the sampling of the discrete correlated ion distributions and the inability to treat the three-dimensional spatial coordinates of the bound ions. In the present study, using a new Monte Carlo-based sampling method for ion distributions, we develop the MCTBI model to overcome these limitations. The key ingredient of the method is to use an “insertion and deletion” algorithm to enhance the efficiency for sampling the important (low-energy) states of the ions while accounting for ion correlation. In the MCTBI model, we use a simple cubic lattice to configure the tightly bound (strongly correlated) ions. We then compute the partition function for the bound ions through the “insertion-deletion” procedure. From the free energy-ion distribution relationship, we predict the average and the most probable distributions (binding sites) for the bound ions and the electrostatic free energies of the system for the different solution conditions.
Applications of the MCTBI model to various systems, including RNAs, RNA-ligand complexes, and RNA-protein complexes, indicate that the MCTBI model is computationally much more efficient that previous TBI models. Comparisons with the experimental results for ion binding properties show the reliability of the model. Furthermore, the MCTBI-predicted ion distribution and binding sites, number of bound ions, and electrostatic free energies for protein-RNA and ligand-RNA complexes provide useful insights into the ion effects in protein/ligand-RNA association, such as the mechanism for the changes of ion binding properties and ion-mediated stabilities upon protein/ligand-RNA association. For example, compared to the unbound RNA, the RNA-protein complex can have more (less) bound ions for low (high) [Mg2+]. However, as a caveat, we note that the current MCTBI model does not treat ion dehydration and chelation effects. Future development of the model should consider these effects. In addition, the current applications of the model has been focused on the ion effects for a given RNA structure. Further development should consider the ensemble of RNA conformations. This goal would demand a more dramatic improvement in the computational efficiency of the MCTBI model.
Supplementary Material
Acknowledgments
This research was supported by NIH grant R01-GM063732 (to SJC) and Zhejiang Provincial Natural Science Foundation China under grant LQ14A040004(to LZS).
Footnotes
Extensive test results for the robustness of the “Insertion-Deletion” algorithm for a variety of RNA structures are presented in the Supporting Information. This information is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Brion P, Westhof E. Hierarchy and dynamics of RNA folding. Annu Rev Biophys Biomol Struct. 1997;26:113–137. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
- 2.Tinoco I, Jr, Bustamante C. How RNA folds. J Mol Biol. 1999;293:271–281. doi: 10.1006/jmbi.1999.3001. [DOI] [PubMed] [Google Scholar]
- 3.Xu XJ, Yu T, Chen SJ. Understanding the kinetic mechanism of RNA single base pair formation. Proc Natl Acad Sci U S A. 2016;113:116–21. doi: 10.1073/pnas.1517511113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rook MS, Treiber DK, Williamson JR. An optimal Mg2+ concentration for kinetic folding of the Tetrahymena ribozyme. Proc Natl Acad Sci U S A. 1999;96:12471–12476. doi: 10.1073/pnas.96.22.12471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Takamoto K, He Q, Brenowitz M. Monovalent cations mediate formation of native tertiary structure of the Tetrahymena thermophila ribozyme. Nat Struct Biol. 2002;9:928–933. doi: 10.1038/nsb871. [DOI] [PubMed] [Google Scholar]
- 6.Sosnick TR, Pan T. RNA folding: models and perspectives. Curr Opin Struct Biol. 2003;13:309–316. doi: 10.1016/s0959-440x(03)00066-6. [DOI] [PubMed] [Google Scholar]
- 7.Woodson SA. Metal ions and RNA folding: a highly charged topic with a dynamic future. Curr Opin Chem Biol. 2005;9:104–109. doi: 10.1016/j.cbpa.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 8.Thirumalai D, Hyeon C. RNA and Protein Folding: Common Themes and Variations. Biochemistry. 2005;44:4957–4970. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 9.Koculi E, Hyeon C, Thirumalai D, Woodson SA. Charge density of divalent metal cations determines RNA stability. J Am Chem Soc. 2007;129:2676–2682. doi: 10.1021/ja068027r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Soto AM, Misra V, Draper DE. Tertiary structure of an RNA pseudoknot is stabilized by diffuse Mg2+ ions. Biochemistry. 2007;46:2973–2983. doi: 10.1021/bi0616753. [DOI] [PubMed] [Google Scholar]
- 11.Stellwagen E, Dong Q, Stellwagen NC. Quantitative analysis of monovalent counterion binding to random-sequence, doublestranded DNA using the replacement ion method. Biochemistry. 2007;46:2050–2058. doi: 10.1021/bi062132w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen AA, Pappu RV. Quantitative characterization of ion pairing and cluster formation in strong 1:1 electrolytes. J Phys Chem B. 2007;111:6469–6478. doi: 10.1021/jp0708547. [DOI] [PubMed] [Google Scholar]
- 13.Chu VB, Herschlag D. Unwinding RNAs secrets: advances in the biology, physics, and modeling of complex RNAs. Curr Opin Struct Biol. 2008;18:305–314. doi: 10.1016/j.sbi.2008.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Draper DE. RNA folding: thermodynamic and molecular descriptions of the roles of ions. Biophys J. 2008;95:5489–5495. doi: 10.1529/biophysj.108.131813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen SJ. RNA folding: conformational statistics, folding kinetics, and ion electrostatics. Annu Rev Biophys. 2008;37:197–214. doi: 10.1146/annurev.biophys.37.032807.125957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Qiu X, Andresen K, Pollack L. Abrupt transition from a free, repulsive to a condensed, attractive DNA phase, induced by multivalent polyamine cations. Phys Rev Lett. 2008;101:228101. doi: 10.1103/PhysRevLett.101.228101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schlatterer JC, Kwok LW, Pollack L. Hinge stiffness is a barrier to RNA folding. J Mol Biol. 2008;379:859–870. doi: 10.1016/j.jmb.2008.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li PTX, Tinoco I., Jr Mechanical unfolding of two DIS RNA kissing comlexes from HIV-1. J Mol Biol. 2009;386:1343–1356. doi: 10.1016/j.jmb.2009.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lipfert J, Sim AY, Doniach S. Dissecting electrostatic screening, specific ion binding, and ligand binding in an energetic model for glycine riboswitch folding. RNA. 2010;16:708–719. doi: 10.1261/rna.1985110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ye W, Yang J, Yu Q, Wang W, Hancy J, Luo R, Chen HF. Kink turn sRNA folding upon L7Ae binding using molecular dynamics simulations. Phys Chem Chem Phys. 2013;15:18510–18522. doi: 10.1039/c3cp53145g. [DOI] [PubMed] [Google Scholar]
- 21.Xia Z, Bell DR, Shi Y, Ren P. RNA 3D Structure Prediction by Using a Coarse-Grained Model and Experimental Data. J Phys Chem B. 2013;117:3135–3144. doi: 10.1021/jp400751w. [DOI] [PubMed] [Google Scholar]
- 22.Denesyuk NA, Thirumalai D. How do metal ions direct ribozyme folding. Nat Chem. 2015;7:793–801. doi: 10.1038/nchem.2330. [DOI] [PubMed] [Google Scholar]
- 23.Serra MJ, Turner DH. Predicting thermodynamic properties of RNA. Methods Enzymol. 1995;259:242–261. doi: 10.1016/0076-6879(95)59047-1. [DOI] [PubMed] [Google Scholar]
- 24.SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc Natl Acad Sci U S A. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mathews DH, Sabina J, Turner DH. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J Mol Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- 26.Chen SJ, Dill KA. RNA folding energy landscapes. Proc Natl Acad Sci U S A. 2000;97:646–651. doi: 10.1073/pnas.97.2.646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zuker MM. Fold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cate JH, Doudna JA. Metal-binding sites in the major groove of a large ribozyme domain. Sturcture. 1996;15:1221–1229. doi: 10.1016/s0969-2126(96)00129-3. [DOI] [PubMed] [Google Scholar]
- 29.Draper DE, Grilley D, Soto AM. Ions and RNA folding. Annu Rev Biophys Biomol Struct. 2005;34:221–243. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 30.Misra VK, Draper DE. A thermodynamic framework for Mg2+ binding to RNA. Proc Natl Acad Sci U S A. 2001;98:12456–12461. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen AA, Draper DE, Pappu RV. Molecular simulation studies of monovalent counterion-mediated interactions in a model RNA kissing loop. J Mol Biol. 2009;390:805819. doi: 10.1016/j.jmb.2009.05.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Auffinger P, Bielecki L, Westhof E. The Mg2+ Binding Sites of the 5S rRNA Loop E Motif as Investigated by Molecular Dynamics Simulations. Chem Biol. 2003;10:551–561. doi: 10.1016/s1074-5521(03)00121-2. [DOI] [PubMed] [Google Scholar]
- 33.Hayes RL, Noel JK, Mohanty U, Whitford PC, Hennelly SP, Onuchic J, Sanbonmatsu KY. Magnesium fluctuations modulate RNA dynamics in the SAM-I riboswitch. J Am Chem Soc. 2012;134:12043C12053. doi: 10.1021/ja301454u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Krasovska MV, Sefcikova J, Sponer J. Cations and Hydration in Catalytic RNA: Molecular Dynamics of the Hepatitis Delta Virus Ribozyme. Biophys J. 2006;91:626–638. doi: 10.1529/biophysj.105.079368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen A, Marucho M, Baker NA, Pappu R. Simulations of RNA Interactions with Monovalent Ions. Methods Enzymol. 2009;469:411–432. doi: 10.1016/S0076-6879(09)69020-0. [DOI] [PubMed] [Google Scholar]
- 36.Sklenovsky P, Florova P, Banas P, Reblova K, Lankas F, Otyepka M, Sponer J. Understanding RNA Flexibility Using Explicit Solvent Simulations: The Ribosomal and Group I Intron Reverse Kink-Turn Motifs. it. J Chem Theory Comput. 2011;7:2963–2980. doi: 10.1021/ct200204t. [DOI] [PubMed] [Google Scholar]
- 37.Do TN, Ippoliti E, Parrinello M. Counterion Redistribution upon Binding of a Tat-Protein Mimic to HIV-1 TAR RNA. J Chem Theory Comput. 2012;8:688–694. doi: 10.1021/ct2005769. [DOI] [PubMed] [Google Scholar]
- 38.Misra VK, Draper DE. On the role of magnesium ions in RNA stability. Biopolymers. 1998;48:113–135. doi: 10.1002/(SICI)1097-0282(1998)48:2<113::AID-BIP3>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 39.Manning GS. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q Rev Biophys. 1978;11:179–249. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 40.Zhou H-X. Macromolecular electrostatic energy within the nonlinear Poisson-Boltzmann equation. J Chem Phys. 1994;100:3152–3162. [Google Scholar]
- 41.Misra V, Draper DE. The interpretation of Mg2+ binding isotherms for nucleic acids using Poisson-Boltzmann theory. J Mol Biol. 1999;17:1135–1147. doi: 10.1006/jmbi.1999.3334. [DOI] [PubMed] [Google Scholar]
- 42.Baker NA, Sept D, McCammon JA. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc Natl Acad Sci U S A. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Baker NA. Improving implicit solvent simulations: A Poissoncentric view. Curr Opin Struct Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 44.Tjong H, Zhou H-X. The dependence of electrostatic solvation energy on dielectric constants in Poisson-Boltzmann calculations. J Chem Phys. 2006;125:206101. doi: 10.1063/1.2393243. [DOI] [PubMed] [Google Scholar]
- 45.Tjong H, Zhou H-X. GBr6NL: a generalized Born method for accurately reproducing solvation energy of the nonlinear Poisson-Boltzmann equation. J Chem Phys. 2007;126:195102. doi: 10.1063/1.2735322. [DOI] [PubMed] [Google Scholar]
- 46.Dong F, Olsen B, Baker NA. Computational Methods for Biomolecular Electrostatics. Methods Cell Biol. 2008;84:843–870. doi: 10.1016/S0091-679X(07)84026-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Joung I, Cheatham TE. Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model specific ion parameters. J Phys Chem B. 2009;113:13279–13290. doi: 10.1021/jp902584c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kuczera K, Jas G, Elber R. The kinetics of helix unfolding: Molecular dynamics simulations with Milestoning. J Phys Chem A. 2009;113:7431–7473. doi: 10.1021/jp900407w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hayes RL, Noel JK, Whitford PC, Mohanty U, Sanbonmatsu KY, Onuchic JN. Reduced Model Captures Mg2+-RNA Interaction Free Energy of Riboswitches. Biophys J. 2014;106:1508–1519. doi: 10.1016/j.bpj.2014.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bai Y, Greenfeld M, Herschlag D. Quantitative and comprehensive decomposition of the ion atmosphere around nucleic acids. J Am Chem Soc. 2007;129:14981–14988. doi: 10.1021/ja075020g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects, and counterion binding–a review of the Poisson-Boltzmann theory and its modifications. Biopolymers. 2008;89:93113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 52.Wang K, Yu YX, Gao GH. Density functional study on the structural and thermodynamic properties of aqueous DNA-electrolyte solution in the framework of cell model. J Chem Phys. 2008;128:185101. doi: 10.1063/1.2918342. [DOI] [PubMed] [Google Scholar]
- 53.Kolculi E, Lee N-K, Thirumalai D, Woodson SA. Folding of the Tetrahymena Ribozyme by Polyamines: Importance of Counterion Valence and Size. J Mol Biol. 2004;341:27–36. doi: 10.1016/j.jmb.2004.06.008. [DOI] [PubMed] [Google Scholar]
- 54.Tan ZJ, Chen SJ. Predicting ion binding properties for RNA tertiary structures. Biophys J. 2010;99:1–12. doi: 10.1016/j.bpj.2010.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mak CH, Henke PS. Ions and RNAs: Free Energies of Counterion-Mediated RNA Fold Stabilities. J Chem Theory Comput. 2013;9:621–639. doi: 10.1021/ct300760y. [DOI] [PubMed] [Google Scholar]
- 56.Henke PS, Mak CH. Free energy of RNA-counterion interactions in a tight-binding model computed by a discrete space mapping. J Chem Phys. 2014;141:064116. doi: 10.1063/1.4892059. [DOI] [PubMed] [Google Scholar]
- 57.Giambasu GM, Luchko T, Herschlag D, York DM, Case DA. Ion Counting from Explicit-Solvent Simulations and 3D-RISM. Biophys J. 2014;106:883–894. doi: 10.1016/j.bpj.2014.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hayes RL, Noel JK, Mandic A, Whitford PC, Sanbonmatsu KY, Mohanty U, Onuchic JN. Generalized Manning Condensation Model Captures the RNA Ion Atmosphere. Phys Rev Lett. 2015;114:258105. doi: 10.1103/PhysRevLett.114.258105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tan ZJ, Chen SJ. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. J Chem Phys. 2005;122:44903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tan ZJ, Chen SJ. Predicting ion binding properties for RNA tertiary structures. Biophys J. 2006;91:518–536. doi: 10.1016/j.bpj.2010.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tan ZJ, Chen SJ. Electrostatic free energy landscape for nucleic acid helix assembly. Nucleic Acids Res. 2006;34:6629–6639. doi: 10.1093/nar/gkl810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tan ZJ, Chen SJ. Minor groove RNA triplex in the crystal structure of a ribosomal frameshifting viral pseudoknot. Biophys J. 2007;92:3615–3632. doi: 10.1038/6722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tan ZJ, Chen SJ. Salt dependence of nucleic acid hairpin stability. Biophys J. 2008;95:738–752. doi: 10.1529/biophysj.108.131524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.He Z, Chen SJ. Predicting ion-nucleic acid interactions by energy landscape-guided sampling. J Chem Theory Comput. 2012;8:2095–2102. doi: 10.1021/ct300227a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zhu Y, Chen SJ. Many-body effect in ion binding to RNA. J Chem Phys. 2014;141:055101. doi: 10.1063/1.4890656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lu XJ, Olson WK. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108C5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. [05/12/2016]; Website address: http://www.rcsb.org/pdb/home/home.do.
- 68.Chen SW, Honig B. J Phys Chem B. 1997;101:9113. [Google Scholar]
- 69.Overbeek J, Th G. Colloids Surf. 1990;51:61. [Google Scholar]
- 70.Stigter D. Biophys J. 1995;69:380. doi: 10.1016/S0006-3495(95)79910-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J Am Chem Soc. 1990;112:6127C6129. [Google Scholar]
- 72.Nymeyer H, Garcia AE. Simulation of the folding equilibrium of a-helical peptides: a comparison of the generalized Born approximation with explicit solvent. Proc Natl Acad Sci USA. 2003;100:13934C13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Hawkins GD, Cramer CJ, Truhlar DG. Solute descreening of solute charges from a dielectric medium. Chem Phys Lett. 1995;246:122C129. [Google Scholar]
- 74.Zou X, Sun Y, Kuntz ID. Inclusion of solvation in ligand binding free energy calculations using the Generalized Born Model. J Am Chem Soc. 1999;121:8033C8043. [Google Scholar]
- 75.Liu HY, Kuntz ID, Zou X. GB/SA scoring function for structure-based drug design. J Phys Chem B. 2004;108:5453C5462. [Google Scholar]
- 76.Liu HY, Zou X. Electrostatics of ligand binding: parameterization of the generalized Born model and comparison with the Poisson-Boltzmann approach. J Phys Chem B. 2006;110:9304C9313. doi: 10.1021/jp060334w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Rosenbluth MN, Rosenbluth AW. Monte Carlo Calculation of the Average Extension of Molecular Chains. J Chem Phys. 1955;23:365–369. [Google Scholar]
- 78.Li Z, Scheraga HA. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc Natl Acad Sci USA. 1987;84:6611–6615. doi: 10.1073/pnas.84.19.6611. [DOI] [PMC free article] [PubMed] [Google Scholar]; Rabow AA, Scheraga HA. Improved genetic algorithm for the protein folding problem by use of a Cartesian combination operator. Proten Sci. 1996;5:1800–1815. doi: 10.1002/pro.5560050906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Westhof E, Sundaralingam M. Restrained refinement of the monoclinic form of yeast phenylalanine transfer RNA. Temperature factors and dynamics, coordinated waters, and base-pair propeller twist angles. Biochemistry. 1986;25:4868–4878. doi: 10.1021/bi00365a022. [DOI] [PubMed] [Google Scholar]
- 80.Grilley D, Soto AM, Draper DE. Mg2+RNA interaction free energies and their relationship to the folding of RNA tertiary structures. Proc Natl Acad Sci USA. 2006;103:14003–14008. doi: 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Conn GL, Gittis AG, Draper DE. A compact RNA tertiary structure contains a buried backbone-K+ complex. J Mol Biol. 2002;318:963–973. doi: 10.1016/S0022-2836(02)00147-X. [DOI] [PubMed] [Google Scholar]
- 82.Krakauer H. The binding of Mg2+ ions to polyadenylate, polyuridylate, and their complexes. Biopolymers. 1971;10:2459–2490. doi: 10.1002/bip.360101209. [DOI] [PubMed] [Google Scholar]
- 83.Romer R, Hach R. tRNA conformation and magnesium binding. A study of a yeast phenylalanine-specific tRNA by a fluorescent indicator and differential melting curves. Eur J Biochem. 1975;55:271–284. doi: 10.1111/j.1432-1033.1975.tb02160.x. [DOI] [PubMed] [Google Scholar]
- 84.Grilley D, Misra V, Draper DE. Importance of partially unfolded conformations for Mg2+-induced folding of RNA tertiary structure: structural models and free energies of Mg2+ interactions. Biochemistry. 2007;46:10266–10278. doi: 10.1021/bi062284r. [DOI] [PubMed] [Google Scholar]
- 85.Serganov A, Yuan YR, Pikovskaya O, Polonskaia A, Malinina L, Phan AT, Hobartner C, Micura R, Breaker RR, Patel DJ. Structural basis for discriminative regulation of gene expression by adenine- and guanine-sensing mRNAs. Chem Biol. 2004;11:1729–1741. doi: 10.1016/j.chembiol.2004.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Leipply D, Draper DE. Effects of Mg2+ on the Free Energy Landscape for Folding a Purine Riboswitch RNA. Biochemistry. 2011;50:2790–2799. doi: 10.1021/bi101948k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Leipply D, Draper DE. Evidence for a Thermodynamically Distinct Mg2+ Ion Associated with Formation of an RNA Tertiary Structure. J Am Chem Soc. 2011;133:13397–13405. doi: 10.1021/ja2020923. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.