Figure 2.
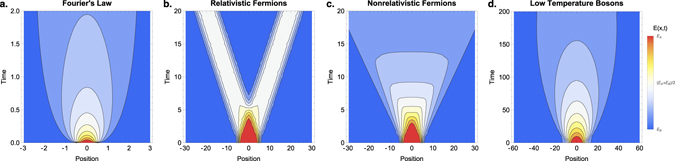
The energy spread of an initial subsystem A at a hot temperature T A (in red) immersed in a cold bath at T B (in blue), for four different theories, computed in d = 1. For the right three panels we performed a lattice computation with L = 200 and L A = 10, so that region A is defined as 5 < x ≤ 5. The colors represent local energy density, and interpolates linearly between E A and E B. (a) The classical Fourier’s law predicts a diffusive spread of the heat, here computed using the heat kernel with region A defined as |x| < 0.5. The temperature difference in subsystem A vanishes diffusively according to ΔT(t) ~ t −1/2. (b) For relativistic fermion systems (T A = 2, T B = 1, n = 0.5) there is instantaneous thermalization once A is in complete causal contact with the bath. (c) In non-relativistic fermion systems (T A = 2, T B = 1, n = 0.5) there is ballistic transport of particles, however, since not all particles have the same speed there is a power-law decay of the initial temperature difference, following ΔT(t) ~ t −1. (d) Non-relativistic boson systems display a crossover from ballistic to diffusive thermalization. Here we show the energy profile in the low temperature regime where diffusive behavior is visible, T A = 100, T B = 0.2 and n = 0.5.
