Figure 3.
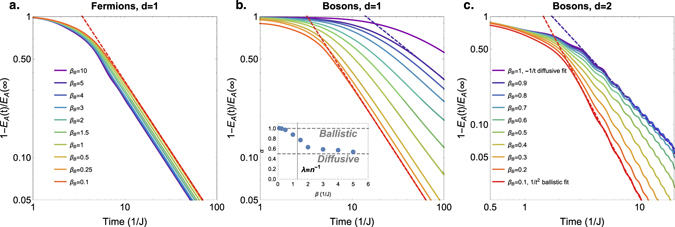
Decay of the energy difference between the system and the bath in non-relativistic fermionic or bosonic systems. In d = 1 (left two pictures) we have immersed a subsystem A at almost infinite temperature β A = 0.01 in a bath with varying temperatures β B. The chemical potential is tuned such that the particle density is n = 1/2, and the total system size is L = 200, and L A = 10. On the vertical axis we plot the energy density in subsystem A, E A(t), normalized by the energy density at infinite time E A(t = ∞). In d = 2 (right picture) the subsystem A has size N A = 6 × 6 in a total system size of N = 48 × 48. (a) In fermionic systems, the decay is always of a ballistic nature, ΔE ~ t −d. (b) In bosonic systems, there is a crossover from ballistic t −d to diffusive t −d/2 decay. We fit the long-time behavior with the power-law form t −α. The inset shows the power α as a function of inverse bath temperature β B. The crossover from ballistic to diffusive occurs around the point β c ~ 1.3 where the thermal de Broglie wavelength λ is comparable to the interparticle spacing n −1, suggesting the wave-like nature of the bosons is responsible for the diffusive behavior. (c) The crossover can also be observed in d = 2 dimensions. The crossover occurs at higher temperatures, since the value where λ ~ n −1/2 has shifted to higher temperature, β c ~ 0.8. Small oscillations with period 1/4 J can be observed due to the specific choice of lattice dispersion.
