Exposure Enriched Outcome Dependent Designs for Longitudinal Studies of Gene-Environment Interaction

Abstract

Joint effects of genetic and environmental factors have been increasingly recognized in the development of many complex human diseases. Despite the popularity of case-control and case-only designs, longitudinal cohort studies that can capture time-varying outcome and exposure information have long been recommended for gene-environment (GxE) interactions. To date, literature on sampling designs for longitudinal studies of GxE interaction is quite limited. We therefore consider designs that can prioritize a subsample of the existing cohort for retrospective genotyping on the basis of currently available outcome, exposure and covariate data. In this work, we propose stratified sampling based on summaries of individual exposures and outcome trajectories, and develop a full conditional likelihood (FCL) approach for estimation that adjusts for the biased sample. We compare the performance of our proposed design and analysis to combinations of different sampling designs and estimation approaches via simulation. We observe that the FCL provides improved estimates for the GxE interaction and joint exposure effects over uncorrected complete-case analysis, and the exposure enriched outcome trajectory dependent design outperforms other designs in terms of estimation efficiency and power for detection of the GxE interaction. We also illustrate our design and analysis using data from the Normative Aging Study, an ongoing longitudinal cohort study initiated by the Veterans Administration in 1963.

1. Introduction

Joint effects of genetic and environmental factors have been increasingly recognized in the development of many complex human diseases [1]. Investigation of gene-environment (GxE) interaction may not only provide biological insights into the etiology of these diseases, but also assist in the discovery of novel genetic or environmental risk factors [2]. However, GxE interaction studies are statistically challenging because of the prohibitive sample size requirement in each GxE configuration. The frequency of the risk allele, the distribution of the environmental exposure, and the effect size of the GxE interaction all contribute to the need for larger samples to detect such an interaction with adequate power [3].

Despite the popularity of case-control and case-only designs, longitudinal cohort studies have long been recommended for GxE interactions because of better characterization of lifetime exposure history [4], the ability to account for within-subject variability of the outcome, and the potential to delineate the dynamic temporal pattern of the genetic or GxE interaction effect, which is often missed in case-control studies by design. Typically, in such studies, extensive information has been collected over the course of the longitudinal follow-up, including prospectively assessed environmental exposures, repeatedly measured outcomes, and a detailed set of potential confounders. We consider a situation where genetic data are to be collected retrospectively with exposures and outcomes already measured; however, our proposed methods can be easily adapted to the collection of new expensive biomarkers of exposure when genetic data is already available. The ability to obtain both genetic and environmental data for all subjects in a large cohort under the budget constraint is often challenging due to cost. To focus the limited resources on informative subjects, there is a need to apply a principled strategy that prioritizes subjects for genotyping or exposure assay. This idea is akin to two-phase sampling designs commonly used for case-control studies, and we extend them to longitudinal cohorts. Such a sampling design is also relevant when constructing an informative subsample using existing electronic health record (EHR) data to check a hypothesis on the interplay between genes and environmental exposures/biomarkers.

As highlighted in a recent commentary by Kraft and Aschard [5], the small number of replicated GxE interactions in observational studies could be attributed to the lack of exposure variability in standard designs. There have been recommendations for exposure enriched sampling in case-control studies with binary exposure. For example, Ahn et al. [6] developed a disease-exposure stratified sampling accompanied by a Bayesian analysis framework, Chen et al. [7] explored several two-phase designs conditional on the exposure and case-control status, and Stenzel et al. [8] evaluated the impacts of exposure enriched sampling designs and exposure measurement error on the power for tests of GxE interaction. All of them concluded with a consensus that an enriched selection of exposed subjects leads to improved power for GxE interactions, as long as exposure measurement error is not severe. Similarly, in cross-sectional studies with continuous exposure and outcome, a substantial reduction in the required number of subjects is achieved by selecting subjects with extreme exposure levels [9]. However, exposure enriched sampling has not been previously studied for longitudinal data, so in this work we aim to characterize the impact of such design on the detection and inferential accuracy of GxE interactions.

In addition to exposure variability, it is also important to consider temporal variation in outcomes when constructing an informative subsample in a longitudinal study. For instance, Schildcrout and Heagerty [10] introduced stratified sampling conditional on a binary response series. Schildcrout et al. [11] proposed auxiliary variable dependent sampling when an inexpensive auxiliary variable related to the longitudinal binary response is available for repeated measures. For longitudinal continuous outcomes, Schildcrout et al. [12] developed outcome dependent sampling that stratifies subjects by the summary measures of the individual outcome vector. In their work, a genetic main effect and a gene-by-time interaction effect were assessed without specific consideration of an environmental exposure. Improved efficiency of estimated coefficients were observed when sampling on a summary measure that is related to the targeted parameters.

To date, literature on sampling designs for longitudinal studies of GxE interaction is quite limited. In this work, we consider designs to select a subsample for genotyping on the basis of available data in an existing cohort/database. Specifically, we propose variants of two-phase designs for longitudinal outcomes, including exposure enriched sampling, outcome trajectory dependent sampling that extends the work of Schildcrout et al. [11] by using a shrinkage estimate, and exposure enriched plus outcome trajectory dependent sampling. We are interested in the GxE interaction, joint exposure effect by genetic subgroups, and potentially the time-varying GxE (GxExT) interaction.

Under the two-phase design, standard maximum likelihood analysis ignoring the sampling mechanism leads to biased estimates [13]. To correct for the biased design, some approaches consider an analysis of Phase II subjects with complete information on exposure, genotype, outcome, and other relevant covariates, and make adjustment using a weighted likelihood or conditional likelihood [10, 12, 14]. In spite of efficiency gains relative to random sampling, subjects with partial information are ignored in these analyses. To recover information on unsampled subjects, some approaches treat it as a missing data problem by incorporating these subjects through an underlying distribution of the missing covariate, either estimated empirically or modeled parametrically [15, 16]; while others use multiple imputation and perform a standard analysis on both observed and imputed data [17], which requires careful consideration of the missing covariate model. Furthermore, a full Bayesian analysis based on the joint likelihood of the entire cohort has been proposed, with a focus on variable selection/dimension reduction in the presence of multiple genetic and environmental factors [6]. In this work, we develop a conditional likelihood-based approach that exploits available data from both phases in conjunction with our proposed designs for longitudinal studies, and investigate their statistical properties in comparison to existing approaches.

We illustrate our methods using data from the Normative Aging Study (NAS), an ongoing longitudinal study of aging initiated by the Veterans Administration in 1963. In this study, subjects who underwent bone lead measurement between 1991 and 2002 were followed up for their blood pressure levels every three years. It has been documented in the existing NAS cohort that lead exposure was associated with increased pulse pressure [18], a marker of arterial stiffness, and this association becomes stronger in subjects who are carriers of the risk alleles of the hemochromatosis (HFE) gene [19]. We use this example to demonstrate the benefits of exposure enriched outcome trajectory dependent sampling for a study of GxE interaction when a quantitative trait in a longitudinal study is of interest.

The rest of the paper is organized as follows. In Section 2, we introduce three sampling designs that can be utilized for longitudinal studies of GxE interaction. Section 3 describes the full conditional likelihood for parameter estimation and statistical inference. In Sections 4 and 5, we perform simulation studies and use the NAS example to evaluate the operating characteristics of our proposed designs and estimation approach, and compare their performances with Schildcrout’s design and analysis. Section 6 concludes with a summary of our findings and discussions.

2. Sampling Designs

Our study objective is to detect and quantify GxE interaction, and the effects of exposure in subgroups defined by levels of genotype, on a continuous trait repeatedly measured in a longitudinal study. We consider a linear mixed effects model suitable for longitudinal data, introduce novel exposure enriched and outcome dependent sampling designs, and develop a likelihood approach to correct for the bias induced by the sampling design.

2.1. Notation

Let Y_ij denote the outcome for subject i measured at the jth follow-up for i = 1, …, N and j = 1, …, r_i. Subject-specific design matrices of covariates for fixed and random effects are denoted by X_i and Z_i respectively. We characterize the response trajectory Y_i = (Y_i1, Y_i2, …, Y_iri)′ via a linear mixed effects model (response model),

$$Y_i=X_i\beta +Z_i{b}_i+{\epsilon }_i$$ (1)

where β is a vector of fixed effects, b_i are subject-specific random effects, ε_i are measurement errors assumed to be normally distributed with mean zero and covariance matrix $R_i={\sigma }_e^2{I}_{r_i}$, and I_ri is the r_i-dimensional identity matrix.

In this setting, X_i is composed of a collection of confounding factors V_i, a variable representing time T_i, a baseline environmental exposure E_i (binary or continuous), a retrospectively collected genotype G_i indicating the presence of the minor allele for a single nucleotide polymorphism (0 = no copy, 1 = at least one copy), and a GxE interaction term G_iE_i, e.g., X_i = (V_i, T_i,E_i,G_i,G_iE_i). Additional interactions between time and exposure- or genotype-related covariates, such as E_iT_i, G_iT_i and G_iE_iT_i, could be included given evidence of significance or scientific justification. While environmental exposures may change over time, we focus on baseline exposure in this present study. Extension to time-varying exposure is mentioned in the discussion.

Under this response model, we allow a random intercept and random slope of time for each subject, so Z_i = (1, T_i) and b_i = (b_0i, b_1i)′ follows a bivariate normal distribution with mean zero and covariance matrix D that contains variance components ${\sigma }_0^2,{\sigma }_1^2$, and a correlation coefficient ρ = corr(b_0i, b_1i). Integrating over random effects, the marginal distribution of the outcome follows a multivariate normal distribution with mean vector μ_i = X_iβ and covariance matrix ${\mathrm{\sum }}_i=Z_{i}D{Z}_i^{\prime }+R_i$, i.e. Y_i|X_i ~ 𝒩(μ_i,Σ_i). Statistical inference for fixed effects can be made by maximizing the marginal likelihood function:

$$L(\beta ,\sigma )=\prod _{i=1}^{N}f(Y_i\mid X_i;\beta ,\sigma )=\prod _{i=1}^N{(2\pi )}^{-\frac{r_i}{2}}·{\mid {\mathrm{\sum }}_i\mid }^{-\frac{1}{2}}·exp\left\{-\frac{1}{2}{(Y_i-X_i\beta )}^{\prime }{{\mathrm{\sum }}_i}^{-1}(Y_i-X_i\beta )\right\}$$ (2)

where f(Y_i|X_i; β, σ) is the multivariate density of Y_i given X_i, and covariance matrix Σ_i with parameters σ = (σ₀, σ₁, ρ, σ_e).

Suppose $(Y_i,X_i^{\ast }),X_i^{\ast }=(V_i,T_i,E_i)$, i = 1, …, N, are collected for the entire cohort in an initial phase (Phase I), followed by a selection of the cohort (with an expected sample size n, n < N) for retrospective genotyping G_i in the second phase (Phase II). Let S_i = 1 (S_i = 0) denote the inclusion (exclusion) of subject i in Phase II. For example, one might assign a constant selection probability P(S_i = 1) = n/N to all subjects and draw samples via independent Bernoulli trials. This sampling scheme renders a missing completely at random pattern for G_i, so the standard maximum likelihood estimation should suffice and be regarded as a baseline for comparison. To investigate how a two-phase design can improve the efficiency of GxE interaction in a longitudinal study, we now describe three sampling schemes that take advantage of observed information in Phase I to guide the sample selection in Phase II.

2.2. Exposure Enriched Sampling

Subjects observed in Phase I are partitioned by their environmental exposures into K mutually exclusive strata R^k, where k = 1, …,K. That is, exposure is the only sampling variable, namely, Q_i = E_i, regardless of the outcome. Within each stratum, individuals are selected with a pre-specified stratum-specific probability π(R^k) = P(S_i = 1|Q_i ∈ R^k) = n_k/N_k, where N_k is the number of subjects falling into stratum R^k, and n_k is the expected number of subjects sampled in Phase II from R^k. For binary exposure (stratum k = E for exposed subjects, and k = Ē for unexposed), subjects with rare exposure are enriched to achieve a certain proportion λ = n_E/n. Note that although a balanced design (λ = 0.5) with a equal number of exposed and unexposed subjects in Phase II is desired, maximum enrichment is bounded by the overall sampling probability and exposure prevalence in the cohort, λ ≤ P(E = 1) · (n/N)⁻¹.

For continuous exposure, subjects are stratified into R^k (k = 1, 2, 3), where $R^1=(E_i\le C_e^1),R^2=\{C_e^1<E_i\le C_e^2\}$, and $R^3=\{E_i>C_e^2\}$. For instance, to draw a sample of n = 250 subjects from the original cohort of N = 1000, one can choose cutpoints $C_e^1$ and $C_e^2$ as the 10^th and 90^th percentiles of the exposure distribution. Subjects from the two tails (strata R¹ and R³) are sampled with a probability of 1.0, and a random sample from stratum R² is drawn to reach the genotyping capacity. However, sampling from fixed tail quantiles with probability 1.0 may not be feasible for a given Phase II sampling budget when the original cohort size is large. In this situation, we suggest first considering the sample size for Phase II and then determining the sampling fractions by reverse calculation so that subjects with extreme exposure levels are sampled with high probabilities.

2.3. Outcome Trajectory Dependent Sampling Using Best Linear Unbiased Predictors of Random Effects

To capture variation in individual outcome trajectory over time, we propose to use the classical best linear unbiased predictors (BLUPs) from a linear mixed model with random intercept and random slope of time as the sampling variable.

Specifically, we first construct a mixed model (sampling model) using Phase I data:

$$Y_i=\alpha X_i^{\ast }+a_i{Z}_i+e_i,i=1,\dots ,N$$ (3)

where α is the vector of population regression coefficients, a_i = (a_0i, a_1i)′ ~ 𝒩(0,D^*) is the vector of subject-specific random effects, and e_i is the measurement error assumed to be normally distributed with mean zero and covariance matrix $R_i^{\ast }={({\sigma }_e^{\ast })}^2·I_{r_i}$. Under this sampling model, empirical BLUPs of random effects for subject i can be obtained by ${\widehat{a}}_i={\widehat{D}}^{\ast }{Z}_i^{\prime }{\widehat{\mathrm{\sum }}}_i^{\ast -1}(Y_i-X_i^{\ast }\widehat{\alpha })$, where α̂, D̂^*, and ${\widehat{\mathrm{\sum }}}_i^{\ast }=Z_i{\widehat{D}}^{\ast }{Z}_i^{\prime }+{\widehat{R}}_i^{\ast }$ are restricted maximum likelihood (REML) estimates for fixed effects α, covariance parameter D^*, and marginal covariance of $Y_i\mid X_i^{\ast }$, respectively. If we treat these REML estimates ${\widehat{\theta }}^{\ast }=(\widehat{\alpha },{\widehat{D}}^{\ast },{\widehat{\sigma }}_e^{\ast })$ as fixed and define $W_i={\widehat{D}}^{\ast }{Z}_i^{\prime }{\widehat{\mathrm{\sum }}}_i^{\ast -1}$, then Q_i is a linear combination of the individual outcome Y_i, i.e., $Q_i={\widehat{a}}_i=W_i{Y}_i-W_i{X}_i^{\ast }\widehat{\alpha }$. Given the marginal distribution assumption for Y_i|X_i in the response model in (1), our sampling variable should follow a normal distribution $Q_i\mid X_i~\mathcal{N}({\mu }_{q_i}=W_i{\mu }_i-W_i{X}_i^{\ast }\widehat{\alpha },{\mathrm{\sum }}_{q_i}=W_i{\mathrm{\sum }}_i{W}_i^{\prime })$, an important property that allows closed-form expression of sampling probability P(S_i = 1|X_i) and hence simplifies computation of conditional likelihood.

If a unvariate sampling variable is considered, say Q_i = â_0i, all subjects in the original cohort are stratified as: R¹ = {â_0i ∈ (−∞, C¹]}, R² = {â_0i ∈ (C¹, C²]}, and R³ = {â_0i ∈ (C²,+∞)}, where strata R¹ and R³ represent two tails of the sampling distribution and cutpoints (C¹, C²) are determined by quantiles of the empirical distribution of Q. When sampling from a bivariate Q_i = â_i, subjects in the central region are stratified into $R^2=\{({\widehat{a}}_{0i},{\widehat{a}}_{1i}):C_0^1<{\widehat{a}}_{0i}\le C_0^2,C_1^1<{\widehat{a}}_{1i}\le C_1^2\}$, while others into R¹ = {(â_0i, â_1i) ∉ R²}. Cutpoints ( $C_0^1,C_0^2,C_1^1,C_1^2$) are determined by grid search of the empirical bivariate distribution of Q, ensuring the fraction of subjects falling into the central region R² matches the fraction in stratum R² given univariate Q_i. Higher selection probabilities are allocated to strata with extreme values of the BLUPs.

Schildcrout et al. [12] sampled subjects based on ordinary least squares (OLS) estimates resulting from subject-specific simple linear regression of individual outcome vectors on time. In contrast, we use BLUPs to account for information at the subject-level while borrowing information from all subjects. OLS estimates for subjects with a small number of repeated measures may be very unstable or even undefined. BLUPs are expected to better characterize the individual outcome trajectory in presence of missing data in that they are essentially shrinkage estimates between subject-specific mean and population average. However, we fix the value of the REML estimates θ̂^*, and so the sampling model for Q_i|X_i does not account for uncertainty in the estimation of θ̂^*. We compared model-based standard errors with empirical standard deviation of point estimates through simulations and found no appreciable difference, suggesting less pronounced practical impact by fixing θ̂^* in the analysis.

2.4. Exposure Enriched Plus Outcome Trajectory Dependent Sampling Using BLUPs of Random Effects

In order to get a larger exposure-outcome variation in the subsample, we also propose designs that combine strategies of exposure enrichment with outcome trajectory dependent sampling using BLUPs, that is, Q_i = (E_i, â_0i)′, Q_i = (E_i, â_1i)′, or Q_i = (E_i, â_i)′. For binary exposure, stratification of subjects and determination of cutpoints can be conducted in a similar fashion as in BLUP-based sampling, conditional on the personal exposure status. For instance, we first define sampling strata R^k,E = {â_0i ∈ (C^k−1,E, C^k,E]} for exposed subjects and R^{k, Ē} = {â_0i ∈ (C^{k−1, Ē}, C^{k, Ē}]} for unexposed, k = 1, 2, 3. Considering the sample size for Phase II, we set stratum-specific selection probabilities so that exposed subjects or those with extreme â_0i are preferentially sampled in Phase II. For continuous exposure, subjects are partitioned into two strata $R^2=\{(E_i,{\widehat{a}}_{0i}):C_e^1<E_i\le C_e^2,C_0^1<{\widehat{a}}_{0i}\le C_0^2\}$ and R¹ = {(E_i, â_0i) ∉ R²}. Likewise, cutpoints for stratification and stratum-specific selection probabilities are chosen to match their counterparts in BLUP-based sampling.

As an extension to the outcome trajectory dependent sampling, personal exposure E_i is observed as a part of X_i, therefore the sampling variable Q_i|X_i indeed follows the same distribution as shown in Section 2.3. This ensures the conditional likelihood accounting for the sampling bias be derived analytically. In addition, we emphasize that although exposure is adjusted in the sampling model in (3) as a fixed effect when sampling based on BLUPs, one can expect that enriching exposed subjects would further increase the exposure-outcome variation in Phase II.

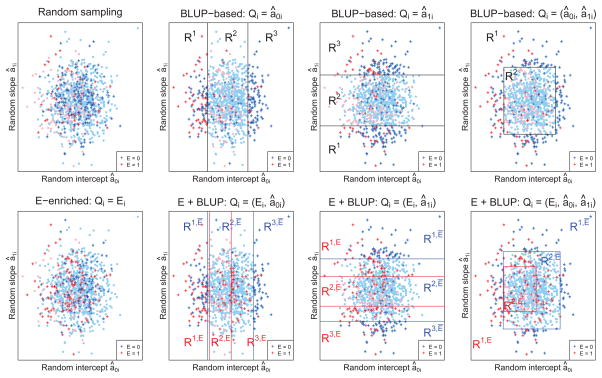
Figure 1 provides a visualization of sample selection under different designs: random sampling, exposure enriched sampling, outcome trajectory dependent sampling using BLUPs of random intercept and/or random slope, and exposure enriched plus outcome trajectory dependent sampling using BLUPs. Here we consider a cohort of 1000 subjects from which 250 are selected for retrospective genotyping. The exposure prevalence in the cohort is 0.2.

Figure 1.

Sample selection under different designs: random sampling, exposure enriched sampling (E-enriched), outcome trajectory dependent sampling using BLUPs of random effects (BLUP-based), and exposure enriched plus outcome trajectory dependent sampling using BLUPs (E+BLUP). In the examples shown here, 250 subjects (+) are sampled from a cohort of 1000 (·), with a exposure prevalence of 0.2.

3. Full Conditional Likelihood for Analysis

After data collection via one of the sampling designs described in Section 2, we partition the sample of N individuals into two groups: subjects {i : S_i = 1} with complete information (Y_i,X_i) and subjects {i : S_i = 0} with partial information (Y_i, $X_i^{\ast }$). To correct for sampling bias from their outcome dependent designs, Schildcrout et al. developed an ascertainment corrected likelihood that considered only subjects with complete information and made adjustments to the likelihood by conditioning on inclusion in Phase II [12], which we refer to as complete-case conditional likelihood (CCL). However, it is known that ignoring data from incomplete-cases (S_i = 0) under a two-phase design leads to estimates not fully efficient [15, 16]. Thus, we propose a full conditional likelihood (FCL), as an extension to the CCL, that accounts for all subjects in hope of improving estimation efficiency. In particular, we expect that observed exposure data on subjects in Phase I can enhance the efficiency of estimates of β_E and β_GE.

In particular, we assume a logistic regression model for binary genotype G_i and let

$$p(G_i\mid X_i^{\ast };\gamma )=\frac{exp(G_i·X_i^{\ast }\gamma )}{1+exp(X_i^{\ast }\gamma )}$$ (4)

denote the probability mass function of G_i given $X_i^{\ast }$ with a nuisance parameter γ. Note that this is a hypothetical model for G_i. Instead of estimating γ from only complete-cases (S_i = 1), we marginalize over the distribution of missing G_i using the joint likelihood with both sampled and unsampled subjects. Extension to polychotomous G_i can be achieved by specifying a multinomial regression model.

The FCL is defined by

$$L^F(\beta ,\sigma ,\gamma )=\prod _{i:S_i=1}f(Y_i,G_i\mid X_i^{\ast },S_i=1;\beta ,\sigma ,\gamma )\prod _{i:S_i=0}f(Y_i\mid X_i^{\ast },S_i=0;\beta ,\sigma ,\gamma ).$$ (5)

Complete-cases contribute to the likelihood through a joint probability of the outcome and genotype conditional on inclusion in Phase II, $f(Y_i,G_i\mid X_i^{\ast },S_i=1;\beta ,\sigma ,\gamma )$; whereas incomplete-cases contribute to the likelihood through a marginal probability of the outcome conditional on exclusion in Phase II, $f(Y_i\mid X_i^{\ast },S_i=0;\beta ,\sigma ,\gamma )$, which is the marginalization of $f(Y_i,G_i\mid X_i^{\ast },S_i=0;\beta ,\sigma ,\gamma )$ over the distribution of G_i.

Using Bayes’ theorem, subject-specific contribution in (5) for {i : S_i = 1} can further be factorized

$$f(Y_i,G_i\mid X_i^{\ast },S_i=1;\beta ,\sigma ,\gamma )=\frac{P(S_i=1\mid Y_i,X_i^{\ast })·f(Y_i\mid X_i;\beta ,\sigma )·p(G_i\mid X_i^{\ast };\gamma )}{P(S_i=1\mid X_i^{\ast };\beta ,\sigma ,\gamma )}$$ (6)

where f(Y_i|X_i; β, σ) is defined by the regression model, $p(G_i\mid X_i^{\ast };\gamma )$ comes from the covariate model in (4), subject-specific selection probability $P(S_i=1\mid Y_i,X_i^{\ast })$ is known for all subjects through stratum membership, and the correction term $P(S_i=1\mid X_i^{\ast };\beta ,\sigma )$ adjusts for biased sampling. In our designs, genotype renders a missing at random mechanism, so $P(S_i=1\mid Y_i,X_i)=P(S_i=1\mid Y_i,X_i^{\ast })$ is independent of parameters (β, σ, γ). Likewise, for unsampled subjects {i : S_i = 0} with G_i missing, their contribution to the FCL is given by

$$f(Y_i\mid X_i^{\ast },S_i=0;\beta ,\sigma ,\gamma )=\frac{[1-P(S_i=1\mid Y_i,X_i^{\ast })]·f(Y_i\mid X_i^{\ast };\beta ,\sigma ,\gamma )}{1-P(S_i=1\mid X_i^{\ast };\beta ,\sigma ,\gamma )}$$ (7)

where $f(Y_i\mid X_i^{\ast };\beta ,\sigma ,\gamma )={\sum }_{G_i\in \{0,1\}}f(Y_i\mid G_i,X_i^{\ast };\beta ,\sigma )p(G_i\mid X_i^{\ast };\gamma )$.

We remind readers that sampling variables based on BLUPs in our proposed designs are linear functions of Y_i. Under the distributional assumption of Y_i|X_i in (1), Q_i|X_i follows a normal distribution with a mean and covariance that depends on parameters β and σ respectively, i.e., Q_i|X_i ~ 𝒩(μ_qi (β),Σ_qi (σ)). Therefore, one can compute the probability of subject i being sampled in Phase II given X_i, as a weighted average of stratum-specific selection probabilities across all strata:

$$P(S_i=1\mid X_i)=\sum _{k=1}^{K}P(S_i=1,Q_i\in R^k\mid X_i)=\sum _{k=1}^K\pi (R^k)P(Q_i\in R^k\mid X_i)$$ (8)

where P(S_i = 1|Q_i ∈ R^k,X_i) = P(S_i = 1|Q_i ∈ R^k) = π(R^k) because sample selection within each stratum is assumed to be independent of X_i|Q_i ∈ R^k. Then, the subject-specific correction term can be obtained by integrating over the set of possible genotypes, $P(S_i=1\mid X_i^{\ast };\beta ,\sigma ,\gamma )={\sum }_{G_i\in \{0,1\}}P(S_i=1\mid G_i,X_i^{\ast };\beta ,\sigma )p(G_i\mid X_i^{\ast };\gamma )$. This ensures the FCL be expressed in a closed form, thereby substantially conveniences the likelihood maximization.

We estimate parameters by direct maximization of the FCL using the Newton-Raphson algorithm. Score functions of the FCL with respect to parameters (β, σ, γ) can be derived analytically due to the normal distribution of Q_i|X_i, and the observed information matrix is calculated as numerical derivative of the score function. We implement this algorithm by the nlm function in R, with initial values of (β, σ, γ) set equal to the standard maximum likelihood estimates based on complete-cases in Phase II. Estimated covariance is calculated numerically after the final Newton-Raphson iteration.

4. Simulation Study

4.1. Description of Simulation Settings

We compared our proposed designs under different simulation scenarios with two alternative sampling schemes, outcome dependent sampling based on OLS estimates from simple linear regressions using single subject data [12], and its extension that additionally enriches exposed subjects in the sample selection. For OLS-based design, we used same sampling variables as described in Schildcrout et al., Q_i = η̂_i, where E[Y_ij] = η_0i + η_1iT_ij = Z_iη_i, i = 1, …,N, and j = 1, …, r_i. For exposure enriched plus OLS-based design, we specified the sampling variable Q_i = (E_i, η̂_i)′. Note that subjects with only one observation do not have OLS estimates from simple linear regressions. Let I be the set of all indices i such that subject i has at least two repeated measures. For subjects i^* with only one observation, we have now assigned η̂_0i^* = y_i^*1 and fixed η̂_1i^* at the mean of the set {η̂_1i : i ∈ I}.

Furthermore, we investigated the performance of our FCL in comparison with three existing complete-case analyses: unweighted uncorrected likelihood (UUL) that handles subjects in Phase II as from a standard prospective cohort, inverse probability weighted likelihood (IPWL) that adjusts for selection bias by weighting subjects by the inverse of their sampling probabilities [14], as well as the CCL of Schildcrout et al. that accounts for the sampling mechanism by conditioning on inclusion in Phase II [12]. Likelihood functions and estimation of UUL, IPWL, and CCL are provided in extended methods of supplementary materials.

We generated individual level data under a balanced design that responses were repeatedly measured at r_i = 5 equally spaced observation times Ti = {T_i1, …, T_i5} = {−1,−0.5, …, 1} for subject i = 1, …,N. We also examined an unbalanced design with a monotone missing pattern such that 10% of remaining subjects were randomly selected to drop out at each follow-up time so that r_i ranged from 1 to 5, and about 65% of subjects in the original cohort were observed at all five follow-up times.

Following the general form of linear mixed model in (1), the marginal mean for subject i is given by:

$$X_i\beta ={\beta }_0+{\beta }_T{T}_i+{\beta }_E{E}_i+{\beta }_{ET}{E}_i{T}_i+{\beta }_G{G}_i+{\beta }_{GE}{G}_i{E}_i+{\beta }_{GT}{G}_i{T}_i+{\beta }_{\mathit{GET}}{G}_i{E}_i{T}_i.$$ (9)

We considered a binary genotype with a minor allele frequency of P(G_i = 1) = 0.1. We examined over a range of combinations for different exposure types (binary/continuous), genotype-environment associations (independent/associated), and interaction models (GxE interaction/ GxExT interaction). We set a prevalence of P(E_i = 1) = 0.2 for binary exposure and a standard normal distribution E_i ~ 𝒩(0, 1) for continuous exposure. When exposure was associated with genotype, we defined the strength of association by a logistic regression model logit{P(G_i = 1|E_i; γ)} = γ₀ + γ_EE_i, where the association parameter γ_E = 0.2 represents an odds ratio of 1.22. To maintain comparability across simulation settings, parameters of fixed effects were selected to explain the contribution of time (10–20%), exposure (5%), genotype (1%), and GxE interaction (0.5–1%) in the variance of outcome. Confounding factors were not considered in our simulation scenarios. We considered a random intercept and a random slope of time Z_i = (1, T_i) for subject i, and set b_i = (b_0i, b_1i)′ ~ 𝒩(0,D), where the variance components ${\sigma }_0^2={\sigma }_1^2=1$ and ρ = 0. The error term ${\epsilon }_i~\mathcal{N}(0,{\sigma }_e^2{I}_{r_i})$ with σ_e = 2.

For simulations with a two-way interaction model, we assumed genotype modifies exposure effect (GxE) that is constant over time, so parameters of fixed effects were set (β₀, β_T, β_E, β_G, β_GE) = (10,−2,−1.5,−1,−1.5) and (β_ET, β_GT, β_GET) = (0, 0, 0). Suppose that only n = 250 subjects from the original cohort of N = 1000 can be sampled in Phase II due to a budgetary constraint. Given the rare binary exposure, exposed subjects were enriched to have λ = 0.5 in Phase II sample. In terms of univariate Q_i, for example, â_0i (or η̂_0i) in BLUP-based (or OLS-based) sampling, we specified stratum size (N₁,N₂,N₃) = (100, 800, 100) and selection probability (π(R¹), π(R²), π(R³)) = (1.0, 1/16, 1.0). For bivariate Q_i, such as (E_i, â_0i)′ (or (E_i, η̂_0i)′), we chose (N_1,E,N_2,E,N_3,E;N_{1, Ē},N_{2, Ē},N_{3, Ē}) = (50, 100, 50; 50, 700, 50) and (π(R^1,E), π(R^2,E), π(R^3,E); π(R^{1, Ē} ), π(R^{2, Ē}), π(R^{3, Ē})) = (1.0, 0.25, 1.0; 1.0, 1/28, 1.0) in exposure enriched plus outcome dependent sampling.

We acknowledge there is the risk of increasing uncertainty when using quantiles of the empirical distribution of â_0i (or â_1i) in the cohort as cutpoints for subject stratification, relative to fixed values from population distribution. However, we want to be realistic in our simulation since the population distribution of â_0i (or â_1i) is unknown in data analysis. We also compared estimates/variance estimates when fixing the cutpoints (see supplemental Table 1) as opposed to quantiles determined from the cohort (supplemental Table 2) and found no qualitative difference, indicating that consequences of ignoring uncertainty in estimation of the cutpoints are negligible in our simulation.

In the three-way interaction model, we assumed a time-varying interaction between genotype and exposure (GxExT) and specified fixed effects parameters as (β₀, β_T, β_E, β_ET, β_G, β_GT, β_GE, β_GET) = (10,−0.7,−1,−1,−0.6,−1,−1,−1.5). Considering the statistical challenge of detecting a three-way interaction, n = 500 subjects from the cohort of N = 5000 were sampled in Phase II for retrospective genotyping. We defined sampling strata using personal exposure and/or BLUP of random effects (or OLS estimates from OLS). While the same exposure enrichment proportion λ = 0.5 was used, we adjusted the stratum size and selection probability in alignment with the genotyping capacity. For example, when Q_i = â_1i or η̂_1i, (N₁,N₂,N₃) = (200, 4600, 200) and (π(R¹), π(R²), π(R³)) = (1.0, 1/46, 1.0); and when Q_i = (E_i, â_0i)′ or (E_i, η̂_0i)′, (N_1,E,N_2,E,N_3,E;N_{1, Ē},N_{2, Ē},N_{3, Ē}) = (100, 800, 100; 100, 3800, 100) and (π(R^1,E), π(R^2,E), π(R^3,E); π(R^{1, Ē}), π(R^{2, Ē}), π(R^{3, Ē})) = (1.0, 1/16, 1.0; 1.0, 1/76, 1.0).

Evaluation metrics

For each examined simulation setting, we generated M = 1000 replicates and evaluated the performance of our proposed sampling designs and analysis approaches by three metrics: bias, relative efficiency, and detection power. Let ${\widehat{\beta }}_{GE}^{(m)}$ and se(β̂_GE)(^m) denote the estimate and standard error of GxE interaction effect, for instance, from replication m, m = 1, …,M. Bias is calculated as the average difference between the estimate and parameter over all replications, $\frac{1}{M}{\sum }_{m=1}^M{\widehat{\beta }}_{GE}^{(m)}-{\beta }_{GE}$. Relative efficiency is estimated as the ratio of mean squared error (MSE) from random sampling with UUL to the MSE from a two-phase design with one of the analyses (UUL, IPWL, CCML, and FCL), say, MSE(β̂_GE)_RS+UUL/MSE(β̂_GE)_BLUP+FCL, where $\mathit{MSE}({\widehat{\beta }}_{GE})=\frac{1}{M}{\sum }_{m=1}^M{\left({\widehat{\beta }}_{GE}^{(m)}-{\beta }_{GE}\right)}^2$. Power quantifies the proportion of correctly rejecting a non-zero effect using a two-sided Wald test at a significance level of 0.05. We also considered additional measures, average standard error $\frac{1}{M}{\sum }_{m=1}^{M}se{({\widehat{\beta }}_{GE})}^{(m)}$, and empirical standard error $\sqrt{\frac{1}{M-1}{\sum }_{m=1}^M{({\widehat{\beta }}_{GE}^{(m)}-{\overline{\widehat{\beta }}}_{GE})}^2}$, where ${\overline{\widehat{\beta }}}_{GE}=\frac{1}{M}{\sum }_{m=1}^M{\widehat{\beta }}_{GE}^{(m)}$, to help assess the validity of our designs and analyses.

4.2. Summary of Simulation Results

We are interested in the modification of exposure effect by genetic subgroups, so we focused results on the detection and estimation of two particular effects: GxE interaction β_GE (or GxExT interaction β_GET given a three-way interaction), and joint exposure effect β_E + β_GE (or β_E + β_ET + β_GE + β_GET given a three-way interaction) among carriers of the risk allele (G_i = 1).

As a validation to previous findings [12, 17], we find that sampling subjects based on estimated intercept (â_0i or η̂_0i) improves estimation precision for β_GE, whereas sampling based on estimated slope (â_1i or η̂_1i) improves estimation precision for β_GET. Therefore, we present here simulation results when Q_i is related to the targeted interaction.

Bias

Table 1 provides estimated bias for GxE interaction and joint exposure effect when the data were generated from a two-way GxE interaction model with a rare exposure and unbalanced data. We find that estimates using CCL and FCL are close to the true parameters in all considered designs, with the largest bias relative to the parameter no greater than 9%. The UUL yields severely biased estimates for β_GE (44% – 149%) when the sampling variable is related to individual mean of the outcome vector (η̂_0i or â_0i), while bias for the joint exposure effect β_E + β_GE appears to be smaller. This is because bias for β_E and β_GE using UUL are always in opposite directions, leading to the estimate for the joint effect of both less biased. IPWL produces modestly biased estimates provided limited sample size in Phase II. For example, under exposure enriched plus BLUP-based sampling, estimated bias of β_GE and β_E + β_GE using UUL are 1.29 and 1.15, as compared to 0.17 and 0.17 using IPWL, respectively. No significant bias was observed under exposure enriched design with the UUL estimates.

Table 1.

Estimated bias for GxE interaction and joint exposure effects using different sampling designs and likelihood approaches. Results are based on 1000 replicates, each including a cohort of 1000 subjects from which 250 are selected for retrospective genotyping. Unbalanced longitudinal outcome is considered, with a monotone missing pattern of 10% random dropouts at each follow-up visit and up to 5 measurements for each subject. Genotype assumed to be independent of personal exposure, with a prevalence of 0.2. β_E = −1.5 and β_GE = −1.5. Estimates biased by at least 10% in bold.

Sampling scheme	Sampling variable	UUL		IPWL		CCL		FCL
		βGE	βE + βGE	βGE	βE + βGE	βGE	βE + βGE	βGE	βE + βGE
Random	-	0.00	0.00	-	-	-	-	-	-
E-enriched	Ei	0.02	0.02	-	-	-	-	0.03	0.02
OLS-based	η̂0i	1.82	−0.31	−0.32	−0.39	0.09	0.06	0.07	0.06
E + OLS	(Ei, η̂0i)	2.23	0.78	0.17	0.15	0.03	0.15	0.05	0.04
BLUP-based	â0i	−0.66	−0.41	−0.67	−0.64	−0.13	−0.13	−0.11	−0.12
E + BLUP	(Ei, â0i)	1.29	1.15	0.17	0.17	0.10	0.09	0.04	0.04

We also examine the impact of sampling designs and likelihood approaches on bias for β_GET and joint exposure effect under a three-way GxExT interaction model (see supplemental Table 3). Likewise, FCL and CCL yield nearly unbiased estimates with small differences to the true parameters, followed by IPWL. Substantial bias for β_ET and β_GET has been observed in the UUL estimates when sampling based on individual slope of time (η̂_1i or â_1i), because subjects with greater temporal variation in the outcome are sampled, bringing bias to the estimated time-varying effects. In other settings not reported in this paper, the benefits of using FCL and CCL are preserved regardless of the exposure type, G-E association, and longitudinal data structure.

Relative efficiency

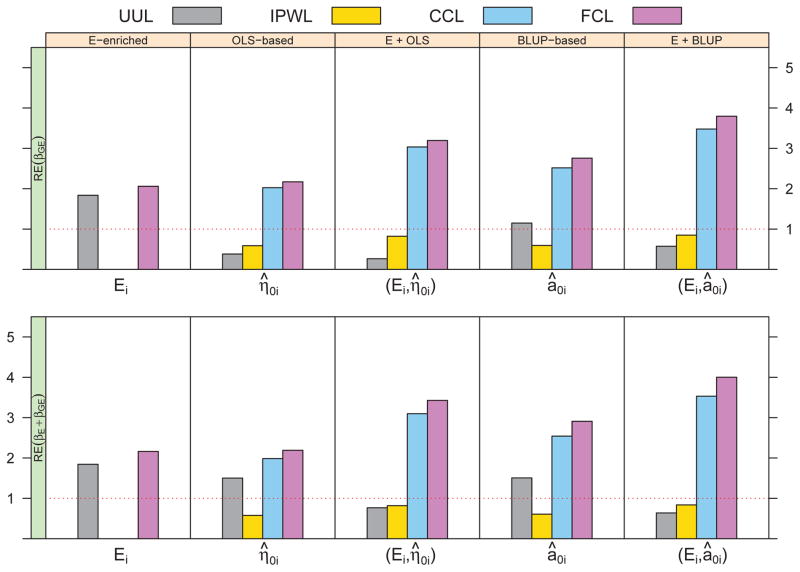
Figure 2 illustrates the estimation efficiency of β_GE and β_E + β_GE under our considered two-phase designs and likelihood approaches, relative to random sampling with the UUL, given rare exposure and unbalanced longitudinal data. We observe that estimation efficiency for β_GE, as well as β_E + β_GE, can be improved via increasing variability of the GxE interaction among sampled subjects by exposure enrichment, or increasing variability of the outcome by sampling towards extreme random intercept â_0i. For example, in the analysis of FCL, relative efficiency for β_GE under exposure enriched and BLUP-based sampling are 2.06 and 2.74, respectively. When considering both exposure and random intercept in the sample selection, a further efficiency gain can be obtained such that the relative efficiency for β_GE and β_E + β_GE exceeds 3.80. In addition, we see more efficient estimates if the sampling variable is related to BLUPs instead of OLS estimates, reflected by 26% (2.74/2.17=1.26) increased efficiency for β_GE using BLUP-based sampling, and 19% (3.80/3.19=1.19) increased efficiency using exposure enriched plus BLUP-based sampling. In simulation settings with balanced outcome, there is little difference in the estimation efficiency between BLUP-based and OLS-based sampling designs (see supplemental Figure 1), indicating BLUPs as shrinkage estimates can better characterize individual outcome trajectory given unbalanced longitudinal data and hence lead to efficiency gains. Similar results have been observed in scenarios with a GxExT interaction using sampling designs based on personal exposure and random slope of time (see supplemental Figure 2).

Figure 2.

Relative efficiency of parameter estimates for G × E interaction and joint exposure effects using different sampling designs and likelihood approaches. Results are based on 1000 replicates, each including a cohort of 1000 subjects from which 250 are selected for retrospective genotyping. Unbalanced longitudinal outcome is considered, with a monotone missing pattern of 10% random dropouts at each follow-up visit and up to 5 measurements for each subject. Genotype assumed to be independent of personal exposure, with a prevalence of 0.2. βE = −1.5 and βGE = −1.5.

It has been reported that the G-E independence assumption can improve estimation efficiency of odds ratio between genotype and exposure in case-control studies [20]. However, in longitudinal studies with continuous outcome, we see no appreciable difference in the relative efficiency of GxE interaction when this independence assumption is violated by a moderate G-E association (results not shown). Moreover, due to increased resolution and biased sampling at two tails, continuous exposure under examined designs shows a similar trend but larger efficiency gains compared to binary exposure. For instance, relative efficiency for β_GE using exposure enrichment with the FCL is 2.06 given a binary exposure, but increases to 2.86 given a continuous exposure.

Using data from unsampled subjects, FCL provides most efficient estimate. While the efficiency improvement of FCL over UUL is modest under exposure enriched sampling (2.06/1.84 = 1.12 for β_GE), it becomes substantial when sampling based on exposure and BLUPs (3.80/0.58 = 6.55 for β_GE). Between two conditional likelihood analyses, FCL increases estimation efficiency over CCL by an additional 5% - 15% under outcome dependent sampling designs. Due to the sandwich-type variance estimate, IPWL is less efficient than CCL, and the naive UUL consistently produces severely biased and insufficient estimate. In addition, we note the impact of sampling design outweighs the impact of analysis provided that sampling bias is appropriately corrected.

Detection power

Table 2 shows the power of detecting a non-zero GxE interaction and joint exposure effect under a two-way GxE interaction model with a rare exposure and unbalanced data. When testing β_GE, oversampling subjects by exposure or random intercept are approximately 50% more powerful than a random selection (~ 0.33/0.22 = 1.50), given appropriate analysis. Moreover, sampling based on exposure and random intercept combined leads to increased power gain that is 1.9 — 2.2 times the power from random sampling. All considered sampling designs with FCL or CCL are adequately powered (> 90%) to detect the joint exposure effect, compared to the 70% power from random sampling. No significant difference has been observed between BLUP-based and OLS-based sampling designs in terms of detection of β_GE and β_E + β_GE using the FCL.

Table 2.

The power (%) of detecting a non-zero GxE interaction or joint exposure effect using different sampling designs and likelihood approaches. Results are based on 1000 replicates, each including a cohort of 1000 subjects from which 250 are selected for retrospective genotyping. Unbalanced longitudinal outcome is considered, with a monotone missing pattern of 10% random dropouts at each follow-up visit and up to 5 measurements for each subject. Genotype assumed to be independent of personal exposure, with a prevalence of 0.2. β_E = −1.5 and β_GE = −1.5.

Sampling scheme	Sampling variable	UUL		IPWL		CCL		FCL
		βGE	βE + βGE	βGE	βE + βGE	βGE	βE + βGE	βGE	βE + βGE
Random	-	22	70	-	-	-	-	-	-
E-enriched	Ei	33	89	-	-	-	-	35	94
OLS-based	η̂0i	2	80	56	81	25	90	34	92
E + OLS	(Ei, η̂0i)	7	42	34	75	29	97	46	98
BLUP-based	â0i	18	69	55	84	32	95	33	95
E + BLUP	(Ei, â0i)	2	25	36	77	41	95	48	96

Comparison among different likelihood approaches suggests that FCL is most powerful at detecting both the GxE interaction and joint exposure effect. We find that the power gain for β_GE from using (exposure enriched plus) BLUP-based sampling over OLS-based sampling is larger in the analysis of CCL (7% from Q_i = â_0i over η̂_0i, and 12% from Q_i = (E_i, â_0i)′ over (E_i, η̂_0i)′) than in the analysis of FCL (1% and 2%), indicating complete-case analysis is more sensitive to the specification of sampling variable in terms of detection power. We note that IPWL tends to have inflated detection power at the cost of reduced efficiency due to the use of sandwich variance estimate. Again, the UUL gives the lowest detection power. We also examined various sampling designs and likelihood approaches under other simulation settings and found no qualitative differences in the operating characteristics.

5. Data Example: the Normative Aging Study

Since year 1991, participants of the NAS were invited to a bone lead assessment using a K-x-ray fluorescence instrument, which provides an index of cumulative lead exposure. The outcome of interest is the difference between systolic blood pressure and diastolic blood pressure (pulse pressure, PP), which was measured at the time of bone lead assessment (baseline, 1991–2002) and followed up every three years until 2013, with a median follow-up of 12.1 years. Indeed, lead exposure has been associated with increased PP [18]. Zhang et al. observed a significant GxE interaction between polymorphisms in the HFE gene and cumulative lead exposure on PP [19]. In this example, we aim to illustrate the utility of exposure enriched outcome trajectory dependent sampling and FCL approach in the analysis of HFE by lead interaction.

We focused on 720 subjects from the NAS cohort who were successfully assessed for cumulative lead exposure at the patella bone and genotyped for the HFE gene. Subjects with compound heterozygotes were excluded because, between two major HFE variant alleles (C282Y and H63D) the association between lead exposure and PP was found to be exclusive among H63D variant carriers (having one or two H63D variant alleles but no C282Y variant allele) [21]. This results in a full cohort of 706 subjects (descriptive characteristics see in Table 3), of whom more than 96% had at least two outcome measurements, contributing to a total of 3265 observations. The majority (97%) of the subjects were Caucasian, with an average age of 66.3 ± 7.2 at the baseline measurement and a risk allele frequency of 21.8%. Patella bone lead concentration was measured continuously, but dichotomized to reflect a relatively rare binary exposure with a prevalence of 0.1 (High: ≥52 μg/g; Low: <52 μg/g).

Table 3.

Baseline characteristics of 706 participants in the Normative Aging Study (NAS)

Variable	Mean ± SD, N (percent)
Baseline age (years)	66.3 ± 7.2
Body Mass Index (kg/m2)	27.9 ± 3.7
Pulse pressure (mmHg)	55.3 ± 15.1
Cumulative patella lead (μg/g)	26.5 [20.8]*
Race (white)	683 (97%)
Education (>12 years)	396 (56%)
Type II diabetes	72 (10%)
Hypertension	447 (63%)
Number of repeated measures on pulse pressure per subject
1–2	137 (19%)
3–4	221 (31%)
5–6	202 (29%)
7–8	146 (20%)

^*Median [interquartile range] for lead exposure whose distribution is right skewed.

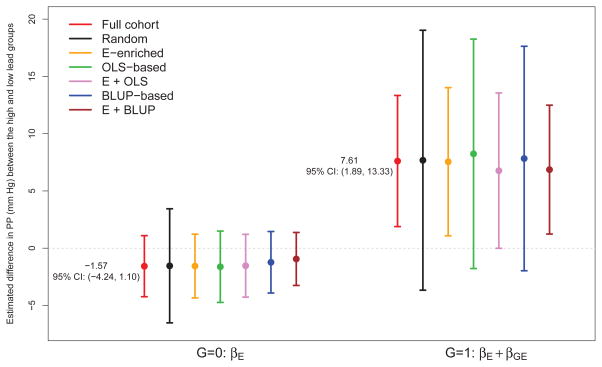
For illustration purposes, we assume that personal genotype data were not available by the end of longitudinal follow-up, and the budget allows retrospective genotyping for only 200 subjects. Full cohort analysis aligned with the findings in Zhang et al. [19] that the mean PP was estimated to be 7.61 mm Hg (95% CI: [1.89, 13.33]) higher for the high patella lead group than the low patella lead group among the H63D variant carriers. For wild types, the difference in the mean PP between the high and low exposure groups was estimated to be −1.57 mm Hg (95% CI: [−4.24, 1.10]). Supported by the the Akaike information criterion (AIC), this analysis used a mixed effects model with random intercept and random slope of time, adjusted for baseline age, body mass index, education level, hypertension, and Type II diabetes in fixed effects.

Besides random selection, we examined five sampling designs. We initially included a lead by time interaction, a H63D by time interaction, and a H63D by lead by time interaction in the mixed model, and found none of these interactions significant in the full cohort analysis, therefore we considered designs that based on random intercept (or OLS estimated intercept) in addition to the exposure enrichment. In particular, we specified stratum sizes (N1;N2;N3) = (71; 564; 71) for outcome trajectory dependent designs (Q_i = â_0i or η̂_0i), and (N_1,E,N_2,E,N_3,E;N_{1, Ē},N_{2, Ē},N_{3, Ē}) = (7, 57, 7; 58, 519, 58) for exposure enriched plus outcome trajectory dependent designs (Q_i = (E_i, â_0i)′ or (E_i, η̂_0i)′). Due to the low exposure prevalence, the maximum stratum size for exposed subjects is N_E = 71 (≈ 706 × 0.1), leading to the proportion of high patella lead subjects in Phase II no greater than λ = 71/200. We used stratum-specific selection probabilities (π(R¹), π(R²), π(R³)) = (1.0, 29/282, 1.0) for univariate Q_i and (π(R^1,E), π(R^2,E), π(R^3,E); π(R^{1, Ē}), π(R^{2, Ē}), π(R^{3, Ē})) = (1.0, 1.0, 1.0; 1.0, 13/519, 1.0) for bivariate Q_i. Because of the superior performance shown in the simulation, we used FCL for the estimation of regression coefficients.

Figure 3 shows average estimated exposure effects among subjects who are carriers of the H63D variant or wild types under different designs based upon 500 replicated Phase II samples. Consistent with simulation studies, we found that point estimates of β_E and β_E + β_GE using FCL were close to results from the full cohort analysis, and estimated efficiency of β_E and β_E + β_GE was considerably improved by our examined designs. For example, we observe that outcome trajectory dependent designs had an estimated relative efficiency of 1.2–1.3 for β_E + β_GE when compared to random sampling with standard analysis, whereas exposure enriched designs were approximately 1.6–2.6 times more efficient than random sampling, given the rare exposure in this example. More importantly, we highlight that incorporation of the exposure enrichment strategy enables detection of the deleterious exposure effect among H63D variant carriers under all three exposure enriched designs. Specifically, the expected PP was estimated to be 7.55 mm Hg (95% CI: [1.08, 14.02]) higher for the high patella lead group among the H63D variant carriers using Q_i = E_i, 6.77mmHg (95% CI: [0.00, 13.55]) higher using Q_i = (E_i, η̂_0i)′, and 6.86 mm Hg (95% CI: [1.43, 12.29]) higher using Q_i = (E_i, â_0i)′. However, this exposure effect, also seen in the full cohort analysis, was considered to be statistically not significant under random sampling or outcome dependent sampling (Q_i = â_0i or η̂_0i). We realize that there could be unmeasured confounders in the NAS cohort, yet their potential influence on the GxE interaction was not addressed in our data analysis.

Figure 3.

NAS results: average estimated exposure effects on the pulse pressure among carriers of the H63D variant (G = 1) or subjects with wild types (G = 0), under different study designs using the FCL (n = 200, N = 706). Personal cumulative lead exposure was measured at patella bone on a continuous scale, and then dichotomized to reflect a rare exposure with a prevalence of 0.1 (High: ≥ 52μ g/g). The numbers on the graph show estimated and corresponding 95% confidence interval of exposure effects by genetic subgroups in a full cohort analysis using linear mixed model with random intercept and random slope of time.

6. Discussion

While novel analysis and powerful tests have been proposed to enhance the detection of multiplicative GxE interaction with repeated measures data [21, 22], it remains relatively less addressed as to how sampling designs affect statistical inference about the GxE interaction in a longitudinal cohort study. In this paper, we described three study designs that prioritize subjects for retrospective genotyping by leveraging environmental exposure information and individual outcome trajectory during the sample selection. We found sampling based upon personal exposure and BLUP of random effect combined can improve estimation efficiency and detection power of the GxE interaction given unbalanced longitudinal data.

We also derived a FCL using data from both phases and compared it with three complete-case analyses. Our results indicate that FCL provides nearly unbiased estimation and enhanced precision (5% – 665% gain in relative efficiency) over complete-case analyses. As an alternative, Schildcrout et al. developed multiple imputation approaches that exploited unsampled subjects in the analysis of two-phase design. Compared to our FCL that marginalizes over the missing genotype on unsampled subjects by a nuisance covariate model, imputation approaches treat missing data as random variables and make random draws from the conditional distribution of the missing data. Our simulation results have shown the benefit of FCL over CCL by 5% – 15% increased estimation efficiency under different simulation setups, which is similar to incremental improvements (2.7% – 20%) provided by imputation approach relative to the CCL in the work of Schildcrout et al. [12]. In addition, imputation based upon observed genotype from a small exposure enriched sample may be hard, and the use of a reference sample (like 1000 Genomes or HapMap) with data on other genes that are potentially correlated with the variant under consideration may improve this imputation.

To characterize individual outcome trajectory, we examined two classes of regression estimates: OLS estimates for intercept and slope of time from simple linear regressions, and BLUPs for random intercept and random slope of time from a linear mixed model. Both classes applied dimension reduction in constructing summary features of the longitudinal outcome, and shared the property that analytical distribution of these features can be derived in a closed form. However, we emphasize that BLUPs can be advantageous, with a 19% – 27% gain in the relative efficiency for the GxE interaction over the OLS estimates when accommodating unbalanced data. This is because OLS estimates use subject-specific information, while BLUPs as shrinkage estimate between the population average and subject-specific mean can borrow strength from other subjects given limited number of measurements, and thus making its estimates more robust to the missing data.

We acknowledge this study has several limitations that could be addressed in the future. First, we focus on a time-stationary environmental exposure, but many such exposures change over time in practice [23]. For cohort studies that collect longitudinal exposure data, it would be helpful to utilize the time-varying exposure to guide the sample selection in Phase II. Inspired by a recent discovery of gene-by-longitudinal environmental exposure interaction in a case-control study [24], one may consider decomposing the time-varying exposure trajectory into a few unrelated components via the functional principal component analysis and explore sampling designs in terms of these components. Secondly, we consider only a linear time trend in the longitudinal outcome with a random intercept and random slope in the sampling model. To handle the possible non-linear time effect, one may regress the outcome on multiple functions of time such as polynomial terms or more general parametric spline basis, and then incorporate these complex smooth features of the outcome trajectory into the sampling mechanism.