Mechanical Trapping of DNA in a Double-Nanopore System

Abstract

Nanopores have become ubiquitous components of systems for single-molecule manipulation and detection, in particular DNA sequencing where electric field-driven translocation of DNA through a nanopore is used to read out the DNA molecule. Here, we present a double-pore system where two nanopores are drilled in parallel through the same solid-state membrane, which offers new opportunities for DNA manipulation. Our experiments and molecular dynamics simulations show that simultaneous electrophoretic capture of a DNA molecule by the two nanopores mechanically traps the molecule, increasing its residence time within the nanopores by orders of magnitude. Remarkably, by using two unequal-sized nanopores, the pore of DNA entry and exit can be discerned from the ionic current blockades and the translocation direction can be precisely controlled by small differences in the effective force applied to DNA. The mechanical arrest of DNA translocation using a double-pore system can be straightforwardly integrated into any solid-state nanopore platform, including those using optical or transverse-current read-outs.

The physical properties of biopolymers like DNA are of fundamental interest as these long molecules are the principal information carriers in all living systems^1,2. Single-molecule force spectroscopy techniques such as optical and magnetic tweezers have been the tool of choice for investigating the mechanical properties of polymers, and their interaction with molecular motors at the single-molecule level.^3–5 These techniques allow for exquisite control over the tension and extension of the biopolymers, but do require handles and anchor points to be chemically engineered onto the biomolecules, increasing complexity and limiting the versatility of these techniques.⁶ Alternative label-free methods to manipulate biopolymers in novel ways at the single-molecule level would be much welcome.

Nanopores are single-molecule force manipulators that not only can exert controlled forces onto biopolymers without the need for handles or labels, but also provide read-out of the biological information encoded in the sequence^7,8. The principle of nanopore sequencing⁹, where an individual DNA molecule is passed in a head-to-tail fashion through a pore while its sequence is locally read, allows for long uninterrupted read-lengths at low copy number and its feasibility has recently been demonstrated by the introduction of a commercial sequencer based on protein nanopores¹⁰. Solid-state nanopores¹¹ are promising for improving such sequencing technology, as they offer benefits in robustness, manufacturing, parallelization, and device integration^12,13. However, the typical residence time of a DNA molecule in a solid-state nanopore is too short to be used for force manipulation studies, let alone to sequence DNA. Although salt gradients¹⁴, unconventional electrolyte conditions^15–17, DNA-nanopore interactions ^18,19, opto-electronic surface-charge modulation²⁰ and plasmonic excitations^21,22 have been shown to increase the residence time of DNA in a solid-state nanopore, there is a clear need for a more radical approach to control the DNA in the nanopore. Previous studies have attempted to achieve this goal with some success. For example, attaching a molecular roadblock to the DNA polymer was shown to transiently halt nanopore translocation^23,24 whereas single-molecule force probes, such as single-molecule tweezers and scanning probes, could balance the force driving the DNA translocation and move the DNA through a nanopore at arbitrary low speed^25–29. However, these techniques for controlling DNA in a nanopore lack throughput, do not allow parallelization, and require DNA labelling, eliminating the advantage the nanopore force spectroscopy techniques has over other conventional techniques.

Here, we present a novel and label-free mechanistic approach for DNA manipulation based on a double-nanopore system, that can slow down and even fully arrest the motion of a single DNA molecule. The key element of our system is two parallel nanopores that are drilled in close proximity (less than 1μm) from each other within the same solid-state membrane (Figure 1a,b). During the electrophoretically driven passage of a DNA molecule through one of the nanopores, the untranslocated part of that molecule can be captured by the second nanopore, leading to mechanical entrapment of the molecule, see Figure 1. The two nanopores exert opposite forces on the DNA that connects them and thus perform a nanoscale tug-of-war on the molecule. This tug-of-war vastly increases the molecule’s residence time within the nanopore sensor, with some molecules being trapped indefinitely (i.e. escaping only when the bias voltage is reversed). Furthermore, by using nanopores of unequal size, we show that the pore of DNA entry and exit can be experimentally discerned, unveiling new insights into the physics of DNA transport.

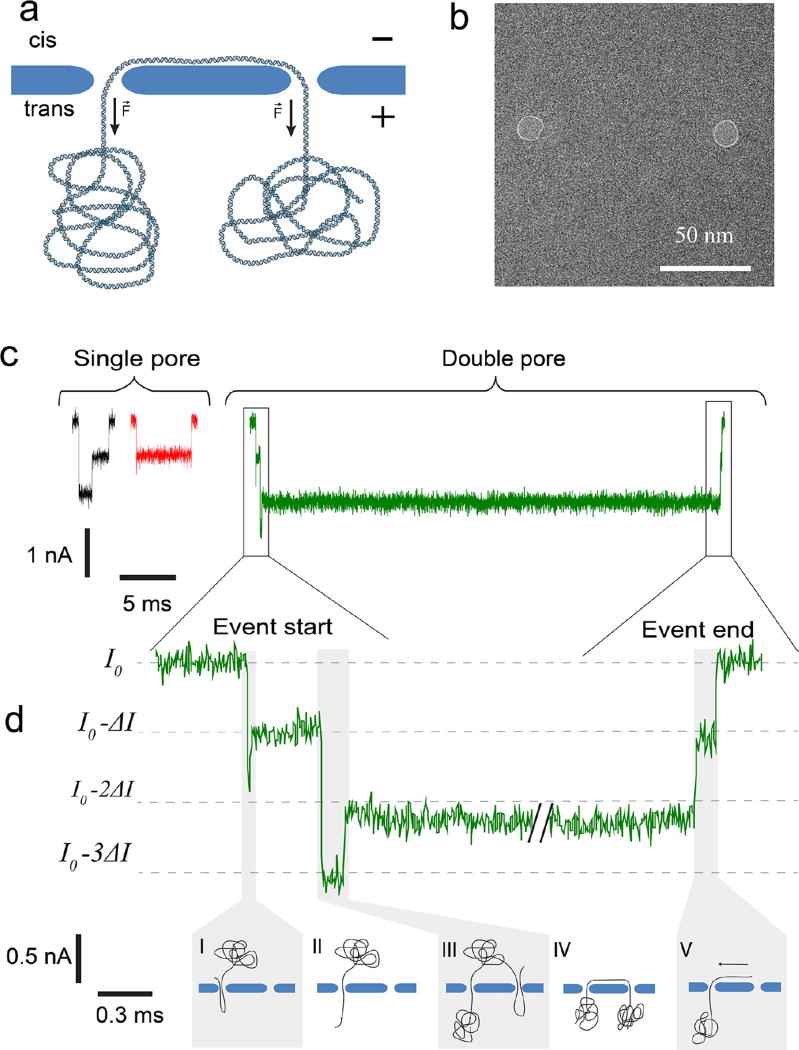
Figure 1.

Concept of trapping DNA in a double-nanopore system. (a) Side-view sketch of a single DNA molecule that is trapped in two nanopores. In a tug-of-war fashion, the forces in the two nanopores cancel out, thus arresting the translocation of the DNA. (b) TEM image of two 10 nm nanopores drilled in a freestanding SiN membrane, separated by 100 nm. (c) Typical examples of single-nanopore and double-nanopore events at a bias voltage of 300 mV, pore diameter of 15 nm, and the pore-to-pore distance of 550 nm. (d) Expanded view of the beginning and ending of the double-pore event. The DNA molecule enters the first nanopore in a folded conformation (I), subsequently traverses it in single-file fashion (II), whereupon a different part of the molecule is captured by the second pore (III) in a folded fashion. Finally, the DNA reaches the trapped state (IV), and eventually slides out (V).

Upon application of a transmembrane bias, an ionic current flows through both nanopores, which permits detection of DNA inside the pores³⁰. Figure 1c illustrates typical DNA translocation events recorded using a double-pore system containing two 15 nm pores separated by 550 nm. Almost without exception, double-pore events last much longer, from 10 ms to 10⁴ ms or even longer than regular DNA translocations (1–3 ms). The double-pore events can be discriminated from regular translocations by the pattern of the ionic current trace at the beginning of the event, the level of the long-duration blockade and, most distinctively, the event ending. A double-pore event begins with multiple changes of a baseline current as the DNA enters each of the nanopores, see the example trace in Figure 1d. (For additional examples see Figures S1 and S2 of Supporting Information.) First, the DNA molecule enters one of the nanopores with its leading end folded (Figure 1d I), as is common for large pores (>5 nm), resulting in two strands of DNA residing in one of the nanopores, whilst the other pore remains open. This produces a double blockade of the current compared to the single blockade level. Subsequently, the DNA fold is pulled through (Figure 1d II), similar to normal DNA translocation. Then, however, the lagging end of the DNA polymer blob is captured into the other nanopore in a folded conformation (Figure 1d III), temporarily leading to a triple blockade level until also this fold is pulled through (Figure 1d IV) resulting in a double current blockade. At this stage, the DNA becomes trapped between the two nanopores, which is topologically similar to the type of stalling that a long DNA molecule experiences during gel electrophoresis³¹. In this phase, the DNA folds are pulled out until the DNA is stretched taut between the two pores, and consequently a tug-of-war is set up between the two nanopores. Eventually one of the nanopores wins the nanoscale tug-of-war and DNA escapes from both nanopores sequentially. After escaping from the first nanopore, there is a short period where DNA resides in only one of the nanopores. The current trace reflects this in a brief single-level blockade (see Figure 1d V), after which the current value reaches the baseline again. The duration of this ending was found to increase with nanopore distance (see Figure S3 of Supporting Information), as expected. The presence of this brief single-blockade-level end signature serves as perhaps the clearest identifier of double-pore events.

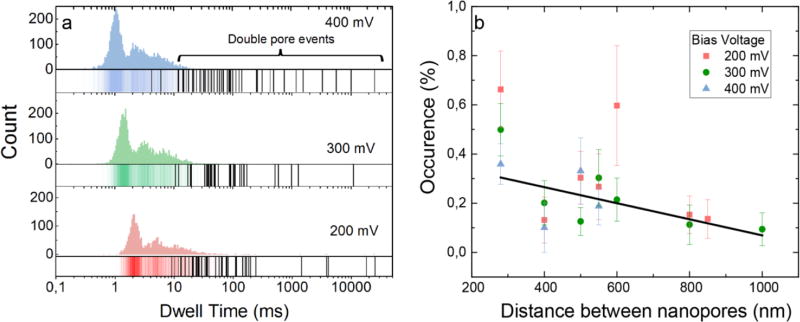
Figure 2a shows the dwell time distribution of all events recorded using a double-nanopore setup, where the double-pore events are highlighted as black lines underneath the histogram. Long events are found to be almost exclusively associated with double-pore events. Note also the occurrence of very long events, lasting several seconds, which were only released upon switching off the bias voltage and hence can be considered as indications of indefinitely trapped DNA molecules. The contribution of double-pore events to the total number of observed events is small, about 0.5%, showing that regular translocations make up the vast majority of the population of events. Although the occurrence of double-pore trapping events is very low, one can still conveniently record tens of such events within half an hour of measurements. The likelihood of observing double-nanopore events decreases with the distance between the pores, see Figure 2b. A control measurement performed using 5 μm-spaced nanopores did not show any double-pore events within the observation time of 30 minutes, during which over 10000 free translocations were registered. The escape velocity of the DNA molecule, deduced from the duration of the end signatures (see Figure S3 from Supporting Information), is in agreement with measurements of DNA translocation velocity reported previously in literature³². The end velocity is found to decrease with increasing distance between the nanopores (see Figure S4 of Supporting Information), which suggests that interactions between DNA and the membrane surface influence the escape speed.

Figure 2.

Experimental event characteristics of the double-pore events. (a) Dwell time distribution of DNA translocations in two 15 nm pores separated by 280 nm. The black lines in the histogram represent the double-pore events. (b) Occurrence rate of double-pore events as a function of distance between nanopores. The black line is a linear fit to the data. Error bars are standard errors.

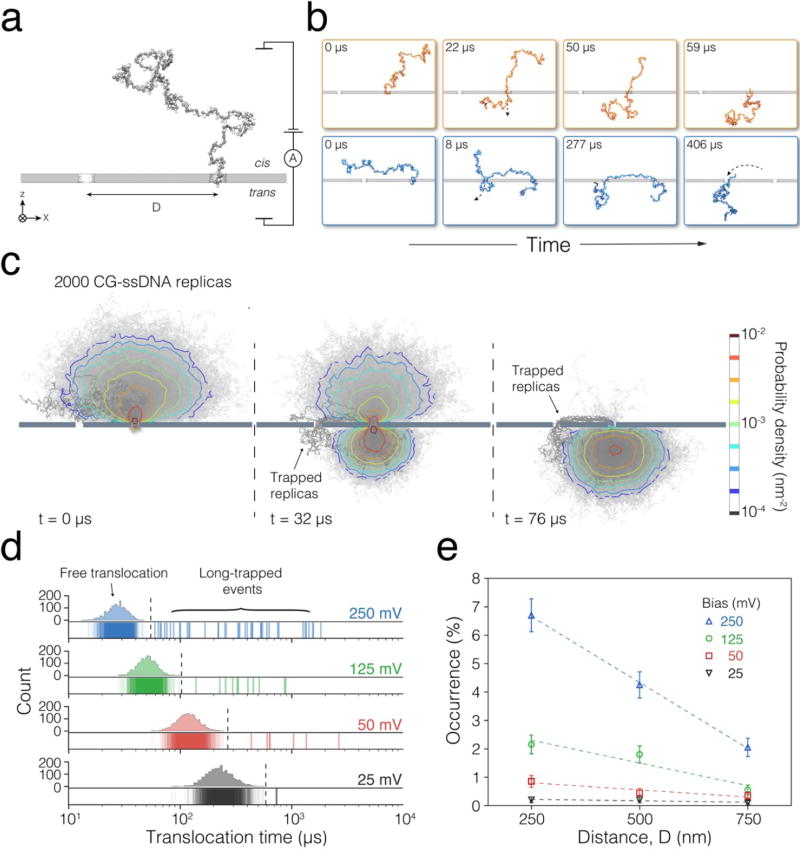
Coarse-grained (CG) molecular dynamics (MD) simulations provided insights into the mechanics of double-pore trapping. In our CG simulations, a single DNA molecule was initially placed at one side (cis) of a solid-state membrane that contained two circular nanopores, with one of the DNA ends entering one of the nanopores (Figure 3a). 2000 independent simulations were run for 2400 μs each in the absence of a transmembrane bias to produce 2000 random DNA conformations. Subsequently, transmembrane bias was turned on and each system was simulated until the entire DNA molecule escaped to the trans side of the membrane (see Methods for a complete description of the MD simulation protocols.)

Figure 3.

Coarse-grained molecular dynamics simulations of DNA capture and translocation in a double-pore system. (a) Setup of the CG simulation. The system consists of two compartments (cis and trans) divided by a solid-state membrane (grey). Two nanopores of equal dimensions are separated by a distance D. A DNA molecule (dark grey) is initially placed in the cis compartment, with one of its ends entering one of the nanopores. A voltage bias is applied across the membrane. (b) Snapshots from two CG MD simulations illustrating a typical single-pore translocation event (top, orange) and a double-pore capture (bottom, blue). (c) Ensemble of DNA conformations observed in double-pore capture and translocation simulations. Shown in grey are the 2000 instantaneous conformations of DNA overlaid with each other. The DNA molecules simultaneously captured by the two pores are highlighted using a darker shade of grey. The color contours specify the density of the CG beads at several stages of the DNA translocation process averaged over the 2,000 replica systems. The density was computed by projecting the DNA beads coordinates onto the XZ plane (the plain passing through both pores normal to the membrane) over 1 nm² grid. (d) Simulated distributions of the DNA translocation time. The DNA translocation time was defined as the time elapsed from the beginning of the simulation (when one end of the DNA was already threaded through one of the pores) until the entire DNA molecule moved to the trans compartment. The translocation times from individual replicas are shown as overlaid vertical bars. The histograms illustrate the distribution of the single-pore translocation times; each histogram contains 40 bins. Dashed lines indicate the time threshold for distinguishing long-lasting events, which is defined as the average translocation time plus 5-fold of the standard deviation of the single-pore translocation durations. The duration of the long-lasting events is show using darker colors. In this particular set of simulations, the scaled-up distance between the nanopores D = 750 nm. (e) Occurrence of the long-lasting events under different pore separations and transmembrane biases. The occurrence is defined as the percentage of long-trapped events among all 2,000 replicas for each simulation condition.

In the large majority of the simulations, the DNA molecules were observed to translocate in the normal fashion where they moved through the nanopore that they were initially threaded in, without having any of the coil interacting with the other nanopore (Figure 3b, top). Double-nanopore events were however observed in a small number of cases, where a part of the DNA molecule was seen to enter the second nanopore, leading to the threading of the lagging part of the DNA into the second nanopore, thus causing the double-pore trapping (Figure 3b, bottom). Supporting Information Movies 1 and 2 illustrate the typical MD trajectories of each type. Plots of the local density of the DNA as a function of the simulation time characterize the ensemble of conformations explored by DNA in the 2,000 independent translocation simulations, see Figure 3c and Supporting Information Movie 3. At the beginning, the DNA conformations form the expected mushroom-like average configuration centered at the nanopore that contains one end of the DNA.³³ As the simulations progress, a mushroom-like cloud of DNA conformations grows at the trans side as the one at the cis side shrinks. Eventually, most of the DNA exits to the trans side while a small number of DNA molecules remain trapped with their two ends threaded through the two nanopores.

The distributions of the simulated DNA translocation times, Figure 3d, exhibit features that are remarkably close to those measured in experiments, cf. Figure 2a. At each transmembrane bias, the individual DNA translocation times histogram form a well-defined cluster, where the cluster’s center shifts toward longer translocation times as the bias decreases, which is the expected behavior for single pore translocations. At the same time, a small but significant number of translocation events last considerably longer than the average. To quantitatively assess the occurrence rate of long-lasting DNA translocation events, we computed the mean and the standard deviation of the single-pore events histograms and defined the long-lasting events as those exceeding the mean single pore translocation time plus five times the standard deviation (see Supporting Information Figure S5 for details). Analysis of the DNA translocation trajectories confirmed that double-pore trapping occurred in all of the long-lasting events. The occurrence of the long-lasting events, Figure 3e, is found to be of order a few percent, to increase with the transmembrane bias, and to decrease with distance between the nanopores, similar to the trends observed in experiments. The numerical difference between the simulated and experimentally measured occurrence can be attributed to the differences between the initial conformations realized in the simulations and experiments, the length of the DNA fragments, and approximations that went into the construction of the CG model (see Methods). Overall, MD simulations verify that double-pore trapping can increase the dwell time of DNA in the nanopore by at least two orders of magnitude in comparison to that produced by single-nanopore translocations.

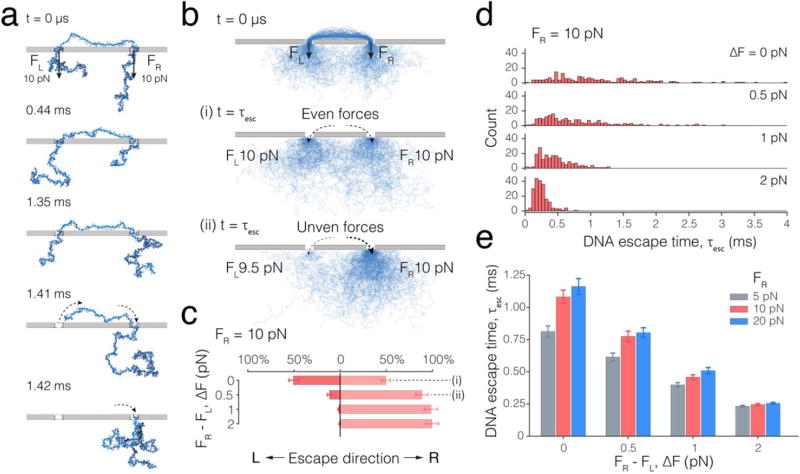
The tug-of-war produced by the double-pore capture of DNA not only slows down the overall DNA translocation process but also offers a means to control the direction of DNA translocation. To demonstrate such control, we considered a situation where a DNA molecule is symmetrically partitioned between the two nanopores, Figure 4a. In contrast to our previous simulations of DNA translocation (Figure 3), the effective forces applied to DNA in the left and right nanopores, F_L and F_R, are now independently controlled. Experimentally, such a force differential can arise from the differences in the nanopore geometry^34,35 and/or surface charge^36,37, and can potentially be externally controlled by optical^20,22 or electrical³⁸ means. When the forces in the two nanopores are exactly equal, the DNA escape process is determined by the diffusive motion of the DNA (Figure 4a), and the differential entropic forces of the two polymer coils^39,40 that develop when the symmetric partitioning of the DNA in the double-pore trap is broken. Hence, the likelihood of DNA exiting from the left or the right nanopore is equal (Figure 4b,i). However, we find that even a very small (0.5 pN) imbalance of the forces considerably affects the direction of the overall DNA motion within the double-pore trap and thus determines the pore from which the DNA exits (Figure 4b,ii). Increasing the force imbalance makes the DNA motion through the double-pore system more unidirectional (Figure 4c) and the DNA escapes faster (Figure 4d). At a 2 pN force differential, which corresponds to only a 20% change of the 10 pN force acting on the DNA in each pore, the DNA was observed to exit through the nanopore of the higher effective force in 199 out of the 200 independent simulations.

Figure 4.

Force-differential control over DNA escape from a double-pore trap. (a) Sequence of snapshots illustrating escape of a DNA molecule from a symmetric double-pore-trapped conformation. At t = 0, a DNA molecule (blue) is threaded through both pores such that the DNA fragments that extend from the two pores to the trans side are of equal length. The backbone beads of the DNA residing within the left and right nanopores experience total net forces F_L and F_R, respectively, directed from cis to trans side, normal to the membrane. In this particular simulation, F_L = F_R = 10 pN. (b) Ensembles of DNA conformations observed during CG MD simulations of DNA escape from a double-pore trap. Shown in blue are 200 instantaneous conformations of DNA overlaid with each other. At t = 0, the DNA molecules are symmetrically threaded through the two pores, similar to the conformation shown in the top snapshot in panel a. (i) Ensemble of conformations adopted by DNA right after escaping (at t = t_esc) to the trans compartment in the case the driving forces in the two nanopores are equal (F_L = F_R = 10 pN). Note that individual escape times vary from one replica to the other, see panel d. DNA escape through either left or right nanopore is equally likely. (ii) Same as above, except that the driving force in the right nanopore is 0.5pN larger than in the left nanopore. The majority of the DNA now escapes through the right pore. (c) The percentage of 200 replica simulations where DNA is seen to escape through either right or left nanopore as a function of the nanopore force differential, ΔF. The force at the right pore was fixed to 10 pN. (d) Distribution of the DNA escape times. The DNA escape time is defined as the time elapsed from the beginning of the simulation until the moment the entire DNA molecule moves to the trans side of the system. The force at the right pore was 10 pN. Bin size of the histograms is 50 μs. (e) Average DNA escape time versus the force differential. The force at the right pore equals 5 pN (grey bar), 10 pN (red bar), and 20 pN (blue bar).

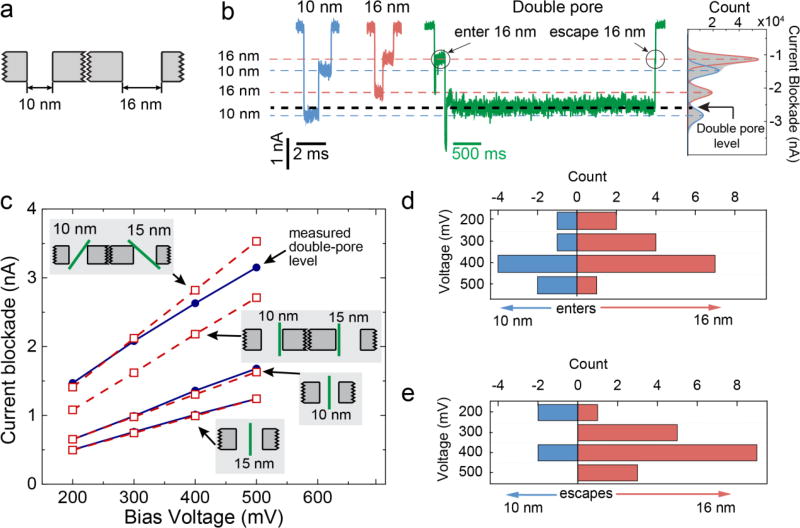
We experimentally created a force imbalance in a double-nanopore system by fabricating two nanopores of different diameters: 10 nm and 16 nm, see Figure 5a (see Supplementary Information Figure S6 for a TEM image). As there is a weak dependence of the electrophoretic force and electroosmotic drag on the pore diameter^34,35,41, we expect the trapped events to end with DNA escaping preferentially from one of the two nanopores. In such an asymmetric double-pore system, double-pore events are clearly observed and constitute about 0.4% of all recorded translocations. Figure 5b shows examples of single and double-pore events and the current blockade histogram of all, single and double-pore, translocations taken at 400 mV (for the histograms of current blockades at other voltages, see Supporting Information Figure S7). Interestingly, the difference between current blockades produced by DNA in either 10 nm or 16 nm nanopores can clearly be distinguished, since the DNA current blockade has a weak dependence on the nanopore size⁴². The DNA current blockade in a 10 nm nanopore is higher than in a 16 nm nanopore and this difference increases linearly with bias voltage. These current blockade differences enable us to discriminate whether DNA is translocating through either the 10 nm or 16 nm nanopore (Figure 5b). Notably, the DNA captured simultaneously by both nanopores produces a current blockade, which is not equal to the doubled blockades produced by DNA in either the 10 or the 16 nm pore. The double-pore current blockade is found to be systematically larger than the sum of the current blockades from the single-pore translocations. We can attribute this effect to a difference in the orientation of the DNA helix within the nanopore. As a DNA molecule trapped in the double-pore is pulled taut onto the membrane and because of its high stiffness (with a persistence length of about 50 nm), we expect it to adopt a tilted orientation in the nanopores, which is different from the freely translocating molecule (see the top inset in Figure 5c). To investigate this, we developed a theoretical model that describes the conductance blockades without any adjustable fit parameters (see Supporting Information Section 7) and explicitly accounts for the orientation of the DNA molecule in the nanopore. Note that our theoretical model does not take into account the surface charge of the nanopore as its effect on the conductance blockade amplitude is minimal in the case of a high-ionic strength electrolyte used in this work. For freely translocating molecules, the model is in excellent agreement with the measured current blockades in both nanopores (bottom 2 lines in Figure 5c), assuming the DNA molecules translocate through the center of the nanopores. Figure 5c shows upper (maximally inclined) and lower (straight hugging of the pore wall) bound estimates for the double-pore blockade level as predicted by the model. At bias voltages below 300 mV, the measured double-pore blockade level is consistent with the resident DNA maximally inclined, as expected. Interestingly however, above 300 mV the observed double-pore level starts to deviate from the model’s predictions, implying a voltage-mediated change in DNA orientation inside the pores. The lower observed double-pore current blockade level indicates a less tilted conformation of the DNA inside the pore, which can be interpreted as voltage-induced bending of DNA that aligns the molecule with the pore axis.

Figure 5.

DNA translocations through asymmetric double nanopores. (a) Schematic of an asymmetric double-nanopore system with two pores of 10 and 16 nm diameters. (b) Example events at 400 mV of freely translocating DNA molecules through the 10 nm and 16 nm nanopores, and a double-pore event. The average current blockade levels (dashed lines) are derived from the peaks in the current histogram of all events, displayed on the far right. (c) Experimental (blue) and theoretical (red) ionic current blockades as a function of bias voltage of the free translocations (bottom two curves) and double-nanopore events (top curves), indicating a voltage-dependent tilted conformation of the DNA when DNA is trapped in the double nanopore. The schematics indicate the orientation of the DNA inside the nanopore for each respective theoretical prediction. (d) Histogram of pore of entry for double-nanopore events. (e) Histogram of the escape directions for double-pore events, showing a clear bias for escape from the larger pore.

The current signatures produced by DNA translocating through differently sized pores allowed us to determine the order in which the DNA entered and escaped during the double-pore events (see Supporting Information Section 8). In most cases, DNA molecules first entered the 16 nm nanopore (roughly 60 % of observed double-nanopore events, see also Figure S10 of Supporting Information for an independent second experiment), as is shown in Figure 5d, which is the expected behavior⁴³. Interestingly, we also observed the DNA molecule to preferentially escape from the 16 nm nanopore (Figure 5e). This is a nontrivial result that, at first sight, appears to contradict the expectation that the larger electrophoretic force inside the 10 nm pore would force the DNA to exit through the smaller pore. A careful consideration of the forces on the DNA in the double-pore system explains the result however. The critical point is that the electric field distribution in the access region near a 10 nm nanopore is different from that of a 16 nm nanopore (See Supporting Information Figure S11). For these relatively large nanopores, the potential drop over the access region can dominate the potential drop over the nanopore itself (see Supporting Information Section 10). Hence, even though the electric field and thus the electrophoretic force inside the 10 nm nanopore is larger compared to the 16 nm one³⁴, the forces exerted on the DNA by the electric field in the access region are significantly larger for the 16 nm nanopore (see Supporting Information Section 11), such that the force differential pushes the DNA towards the 16 nm pore. Note that, because DNA is highly bent in the double-pore-trapped conformation, the total force on the DNA molecule is not solely determined by the transmembrane bias²⁵. For the asymmetric double-pore system, our observations (Figure 5e) indicate that such force imbalance indeed determines the tug of war and results in preferred escape through the 16 nm nanopore. The asymmetric double nanopore system thus enabled us to determine and control the entry and escape direction of a DNA molecule trapped in a double nanopore.

To conclude, we developed a novel approach to mechanical trapping of DNA in solid-state nanopores, which can vastly increase the residence times of the molecules, with some molecules being trapped indefinitely. The double nanopore platform not only allows for slowing down DNA molecule translocations, but also unveils interesting physics of this nanoscale tug-of-war on DNA, that we corroborate with MD simulations and theoretical modelling. We show that, for differently sized nanopores, we can monitor the entry and escape direction of the stalled DNA molecule, which are dictated by the size asymmetry between the two pores. The purely mechanical stalling of the DNA translocation with the double-pore approach holds great potential for future biophysics experiments and nanopore applications. The approach is straightforward to upscale and is easily incorporated in any solid-state nanopore platform, where the slowed down molecule allows the long integration times required for optical²² or transverse⁴⁴ read-out of its sequence. The control over the translocation direction by applying minute force differences between the pores may permit re-addressing the same DNA fragment multiple times, for example for re-sequencing when generalized to single-stranded DNA. Ultimately, the sliding speed of the DNA molecule past the nanosensor can be controlled at will by the experimenter by addressing each of the nanopores independently, which will be the focus of our future work.

Methods

Double-pore experiments

Double nanopores were fabricated by drilling two nanopores in close proximity within the same freestanding membrane, made of 20 nm-thick low-stress SiN. A TEM image of the typical double-pore device is shown in Figure 1(b). During the experiments DNA is placed into the cis compartment and it is dragged through the nanopore by biasing the Ag/AgCl electrode on the trans side. Throughout all the experiments we used λ-DNA (48kbp, contour length 16.3 μm) in 2M LiCl buffers with 20mM Tris and 2mM EDTA. Most of the experiments were carried out using 15 nm nanopores, unless specified otherwise. The distances between the nanopores were chosen to be roughly smaller than the diameter of gyration of the λ-DNA coil, which is approximately 800 nm³⁹. The double-pore events were extracted from ionic current traces using Tranzalyser⁴⁵ and analysed using a custom-made software.

Coarse-grained MD simulations

All CG MD simulations were performed using a previously described custom CG model⁴⁶. Although this CG model was originally developed to describe the behaviour of unstructured single-stranded DNA, it can also describe the behaviour of much larger dsDNA molecules through scaling of the simulation length scales with the ratio of the persistence lengths of the molecules, i.e., by a factor of 50. The time scale of the CG simulations was calibrated by matching the experimental⁴⁷ and simulated electrophoretic mobility of DNA. The electrolyte conditions were taken into account implicitly through calibration of the CG model to MD simulations and experiments.⁴⁶ All distances and time intervals reported in the manuscript have been scaled to describe the behavior of dsDNA. The steric forces from the inorganic membrane and the forces produced by the transmembrane bias were applied through grid-force potentials⁴⁸ using a method described previously²² and the solvent was modelled implicitly via a Langevin thermostat. Supporting Information provides a complete description of the simulation protocols.

Theoretical model of the conductance blockade

To theoretically compute the blockade-current amplitude for a given orientation of the DNA in a nanopore, the nanopore volume was divided into cylindrical slabs of the same height arranged perpendicular to the nanopore axis. The resistance of each slab was computed by integrating the local resistance of the solution within the slab, which in turn was computed using a previously established dependence of the ion mobility and ion number density on the distance from the DNA molecule⁴⁹. The total resistance of the nanopore volume was computed by summing up the resistances of all slabs. The ionic current blockades were computed by taking into account both the resistance of the nanopore volume and the access resistance of the solution. Supplementary Information provides a complete description of the theoretical model.