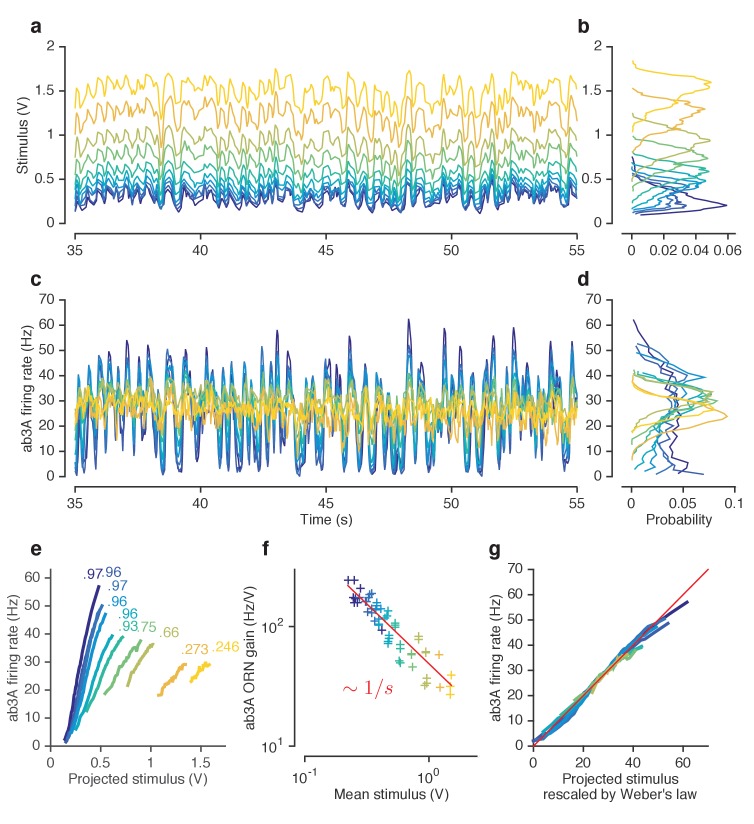
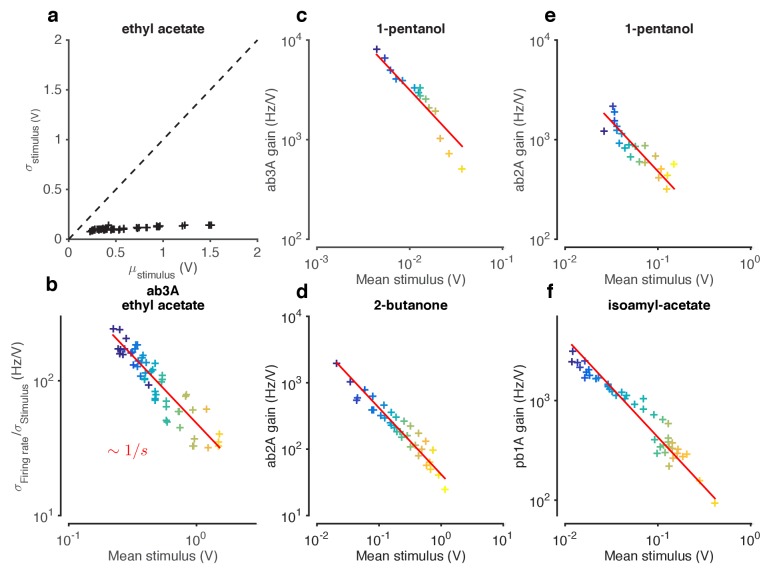
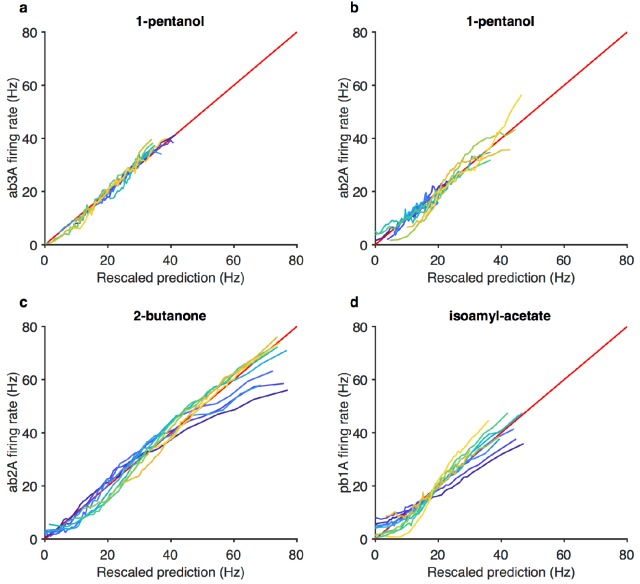
Figure 3. ORNs decrease gain with stimulus mean, consistent with the Weber-Fechner Law.

(a) Ethyl acetate stimuli with different mean intensities but similar variances. Stimulus intensity measured using a Photo-Ionization Detector (PID), units in Volts (V). Colors indicate mean stimulus intensity. (b) Corresponding stimulus distributions. (c) ab3A firing rate responses to these stimuli. (d) Corresponding response distributions. (e) ORN responses vs. stimulus projected through linear filters. Colored numbers indicate $r^2$ between linear projections and ORN response. (f) ORN gain vs. mean stimulus for each trial. Red line is the Weber-Fechner prediction (${\displaystyle \mathrm{\Delta }R/\mathrm{\Delta }S\sim 1/S}$) (g) After rescaling the projected stimulus by the gain predicted by the red curve in (f), and correcting for an offset, ORN responses collapse onto one line. n = 55 trials from 7 ORNs in 3 flies. All plots except (f) show means across all trials. (f) shows individual trials.

DOI: http://dx.doi.org/10.7554/eLife.27670.010

Figure 3—figure supplement 1. Weber-Fechner Law broadly observed across odor-receptor combinations.

(a) Standard deviation vs. mean of ethyl acetate stimulus in Figure 1. (b) ORN gain estimated by the ratio of standard deviation of firing rate to standard deviation of stimulus, vs. mean stimulus in each trial. This model-free estimate of ORN gain ignores kinetics of response, but returns similar estimates of the gain (cf. Figure 3f). Note that the units of gain estimated this way are the same. (c–f) ORN gain as a function of mean stimulus for various odor-receptor combinations. In all plots, the red line is a power law with slope −1 (the Weber-Fechner Law). Data in panel a and b is the same as in Figure 3. n = 121 trials from 16 ORNs in 6 flies.

DOI: http://dx.doi.org/10.7554/eLife.27670.011

Figure 3—figure supplement 2. Ability of NL models to reproduce observed change in input-output curves.

(a–c) Static NL model responses. (a) The input nonlinearity of NL model is chosen to be a Hill function with n = 1. (b) Filter of NL model, measured directly from the data. (c) NL model responses vs. projected stimulus. While these curves appear to change slope with increasing mean stimulus, mean responses also tend to increase (purple … yellow). (d–f) Varying NL model responses, where the K_D of the input nonlinearity is allowed to vary with the mean stimulus. (d) Input nonlinearities for stimuli with different mean (colors). The K_D of each curve is set to the mean stimulus of that trial. (e) Filter of NL model, same as in (b). (f) Model responses vs. projected stimulus. Note that, like in the data (cf. Figure 2e), the mean response remains relatively invariant with mean stimulus, and that curves get shallower with increasing mean stimulus. (g) Comparison of steady state gain (slope of functions shown in (a) and (d)) when K_D is fixed (black) and when K_D is allowed to vary with the mean stimulus (red). When K_D is fixed, the the relationship between gain and mean stimulus approaches a power law with exponent 2 (gain ~ $\frac{K_D}{{(S+K_D)}^2}$). However, when $K_D$ varies with the mean stimulus, the steady state gain ~ $\frac{1}{S}$, which is the Weber-Fechner Law.

DOI: http://dx.doi.org/10.7554/eLife.27670.012

Figure 3—figure supplement 3. Projected stimulus rescaled by Weber-Fechner relation correlate with firing rates.

(a–d) Firing rate vs. projected stimulus rescaled by Weber-Fechner relation (as in Figure 3g) for four additional odorant-receptor combinations. Red line is the line of unity. Same data asin Figure 3—figure supplement 1c–f.

DOI: http://dx.doi.org/10.7554/eLife.27670.013