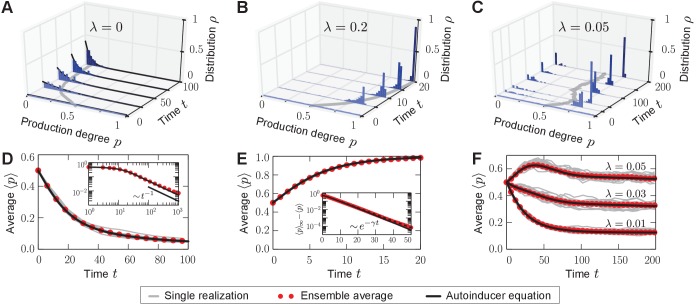
Figure 2. Homogeneous and heterogeneous production of autoinducers in the quorum-sensing model.

Temporal evolution of autoinducer production in the quorum-sensing model depicted as histograms of production degrees (normalized values), (A–C); and average production level of autoinducers in the population (D–F); see also Videos 1–3. (A) In the absence of sense-and-response (${\displaystyle \lambda =0}$), only non-producers proliferate. The approach to stationarity is asymptotically algebraically slow for a quasi-continuous initial distribution of production degrees (D). The black line $⟨p⟩\sim t^{-1}$ serves as a guide for the eye. (B) Sense-and-response through quorum sensing ($\lambda =0.2$ here) promotes autoinducer production, and the population becomes homogeneous (ultimately, fixation at a single production degree, data not shown). The response function used here, $R(⟨p⟩)=⟨p⟩+0.2\cdot \sin (\pi ⟨p⟩)$, was chosen such that an individual’s production degree is always up-regulated through quorum sensing (see Figure 1B). Approach to stationarity is exponentially fast (E), but timescales may diverge at bifurcations of the response function (see Appendix 1—figure 3). The dashed line in (E) shows fit to an exponential decay. (C) When $\lambda$ is small ($\lambda =0.05$ here), the population becomes heterogeneous: quasi-stationary states arise in which the population splits into two subpopulations, one of which does not produce autoinducers, while the other does. The same monostable response function was chosen as in (B). Therefore, heterogeneity may arise without bistable response. For very long times, one of the two absorbing states (A, B) is reached, data not shown (see Figure 3A). Heterogeneous, quasi-stationary states arise for a broad class of initial distributions (see Appendix 1—figure 1 and our mathematical analysis). At the same time, the average production level of autoinducers in the population is adjusted by the response probability $\lambda$ if $s$ is fixed (F) or vice versa (data not shown). Bimodal, quasi-stationary states also arise when noisy inheritance, noisy perception, and noisy response are included in the model set-up (see Appendix 1—figure 2). Mean-field theory agrees with all observations (autoinducer equation (1)). The time unit $\mathrm{\Delta }t=1$ means that in a population consisting solely of non-producers, each individual will have reproduced once on average. Ensemble size $M=100$, $s=0.2$, $N={10}^4$.

DOI: http://dx.doi.org/10.7554/eLife.25773.006