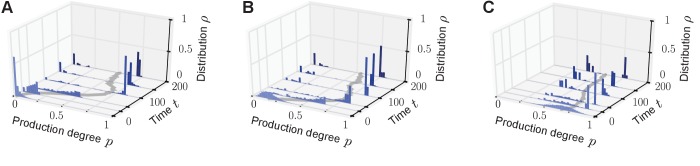
Appendix 1—figure 1. Phenotypic heterogeneity in the quorum-sensing model arises for diverse initial distributions.

Bimodal quasi-stationary states arise for a broad class of initial distributions if the value of the response probability $\lambda$ is small and an individual’s production degree is upregulated by the sense-and-response mechanism through quorum sensing (${\displaystyle R(p)>p}$ for some $p\in [0,1]$). Depicted is the temporal evolution of the histograms of production degrees (normalized values) as in Figure 2 of the main text. The monostable response function $R(p)=p+0.2\cdot \sin (\pi p)$ was chosen (see Figure 1B). (A, B) $\lambda =0.05$. Initially, the population consists of mainly non-producers (in (A) initial distribution ${\displaystyle p_i\sim \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(0.5,20)}$ i.i.d. and in (B) initial distribution ${\displaystyle p_i\sim \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(4,20)}$ i.i.d.). Due to the balance of fitness differences and sense-and-response through quorum sensing, the population splits into a heterogeneous population with producers and non-producers coexisting for long times. (C) $\lambda =0.02$. If the initial distribution of production degrees is centered around high production degrees (initial distribution ${\displaystyle p_i\sim \mathrm{B}\mathrm{e}\mathrm{t}\mathrm{a}(10,5)}$ i.i.d.), the population may still evolve in time into a heterogeneous quasi-stationary state. However, the peak at the low-producing degree is typically located away from 0, that is, ${\displaystyle p_{\mathrm{l}\mathrm{o}\mathrm{w}}>0}$. These exemplary numerical results (A–C) are confirmed by the results of our mean-field theory: heterogeneous stationary distributions are the attractor of the mean-field dynamics (autoinducer equation (1) in the main text) for a broad range of initial distributions if conditions (i) ${\displaystyle R({\overline{p}}_{\mathrm{\infty }})=p_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}>{\overline{p}}_{\mathrm{\infty }}}$ and (ii) ${\displaystyle \lambda <{\lambda }_{\text{up}}=s/2}$ are fulfilled (see main text). Note that ‘i.i.d.’ abbreviates ‘independent and identically distributed’. Parameters: selection strength $s=0.2$ and population size $N={10}^4$.

DOI: http://dx.doi.org/10.7554/eLife.25773.013