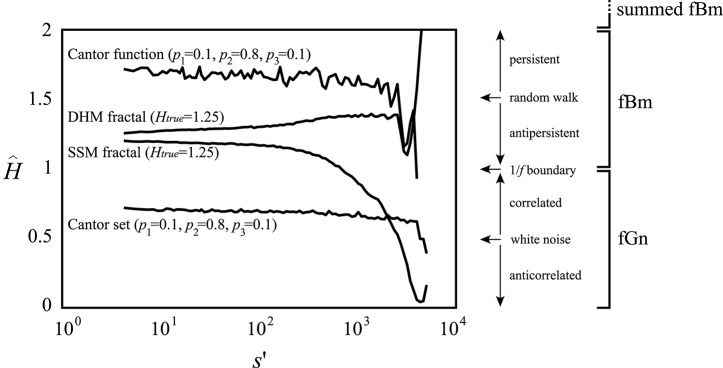
Figure 1.

Scale-invariance cannot be revealed within inadequate scaling ranges. On synthesized monofractal signals of length N = 2¹⁴, the Hurst exponent as the measure of monofractality was estimated by the SSC method (Eke et al., 2000) within a temporal window with a lower boundary, s′, and an upper boundary set to N/2. The estimate of the generalized Hurst exponent at q = 2 [H(2)] was obtained on multifractal signals by the FMF-SSC method (Mukli et al., 2015) within the same range of scales. DHM fractal: synthesized by the method of Davies and Harte (DHM; Davies and Harte, 1987) at H_true = 1.25; SSM fractal: synthesized by the SSM method (Saupe, 1988); Cantor set and function generated at appropriate weight factors p₁, p₂, p₃ (Cantor, 1883; Mandelbrot, 1982). Estimated Hurst and generalized Hurst exponents are displayed on an extended scale within the range of [0, 2]. Signal classes based on the extended H and H(2) are shown to the right for reference. Contracting scaling range—by increasing s′—will render the information remaining in the signal for its analysis inadequate to demonstrate its scale-invariance (see the bias in reference of H_true progressively increasing with s′). A standard treatment of scaling function multimodality typically results in contracted scaling ranges and thus results in a loss of valuable information on fractal scaling.