Figure 2.

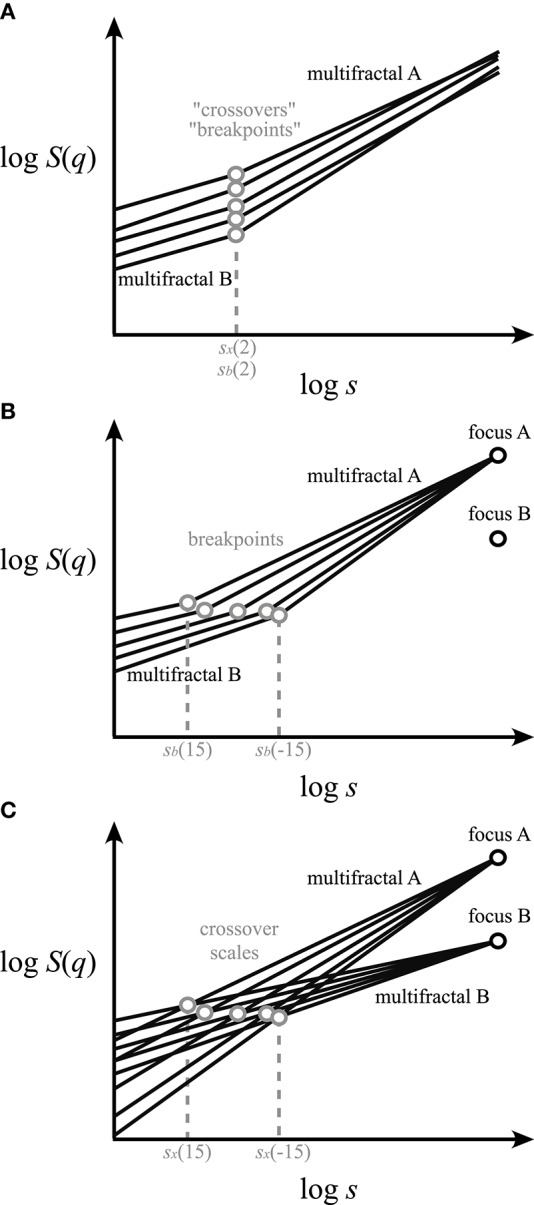
Different concepts for handling multifractal crossover. Exact scaling functions (solid lines) for a range of qs are shown in log-log plots. The components (multifractals A,B) separated by breakpoints—at the scale s_b—and by crossovers—at the scale s_x—are marked as gray circles. (A) Approaches in the literature for finding “crossovers” or “breakpoints” of bimodal multifractals along a single scaling function [i.e., log S(2)] should be regarded as vaguely defined (Schumann and Kantelhardt, 2011). (B) Our concept of q-wise scaling range adaptive focus-based multifractal formalism. This approach employs iterative fitting for q-dependent crossover scales by enforcing the focus (black circle) of the scaling functions found at maximum signal length. Note that the point-like q-wise breakpoints separate two adjacent SRs occupied by distinct scale-invariant components of the multifractal scaling functions. (C) Scaling function decomposition with focus-based multifractal formalism utilizing an extended version of the iterative approach shown in (B). It yields a complete decomposition of the overlapping scaling functions of the merging fractals/multifractals coexisting within the same SR.