Martini Coarse-Grained Force Field: Extension to RNA

Abstract

RNA has an important role not only as the messenger of genetic information but also as a regulator of gene expression. Given its central role in cell biology, there is significant interest in studying the structural and dynamic behavior of RNA in relation to other biomolecules. Coarse-grain molecular dynamics simulations are a key tool to that end. Here, we have extended the coarse-grain Martini force field to include RNA after our recent extension to DNA. In the same way DNA was modeled, the tertiary structure of RNA is constrained using an elastic network. This model, therefore, is not designed for applications involving RNA folding but rather offers a stable RNA structure for studying RNA interactions with other (bio)molecules. The RNA model is compatible with all other Martini models and opens the way to large-scale explicit-solvent molecular dynamics simulations of complex systems involving RNA.

Introduction

Ribonucleic acid (RNA) plays a crucial role in gene expression by actively regulating protein synthesis. Both the sequence and tertiary structure of RNA molecules are important in determining how RNA interacts with other biomolecules and influences, e.g., gene expression. Genome-wide studies of transcriptomes have shown that RNA tertiary structure can affect protein expression and RNA stability (1). Noncoding RNAs, for example, can be recognized by proteins or large RNA molecules through molecular interactions involving short nucleotide sequences (2, 3, 4). To study RNA-protein structural assemblies and RNA complexes like the ribosome requires computational tools that are capable of efficiently modeling large length- and timescales. The challenges in dealing with the complex and diverse structural motifs of RNA are big and require multiresolution models (5).

Atomistic molecular dynamics (MD) simulations are currently the method of choice for computational studies of protein-DNA/RNA complexes. Recent developments in DNA and RNA force fields have improved their capabilities in the description of sequence-dependent structural variability (6, 7, 8, 9, 10, 11). Atomistic MD simulations are limited, however, by their computational cost and sufficient sampling of systems larger than a few tens of basepairs. Proper use of enhanced sampling methods can help extend the reach of atomistic nucleotide simulations, but they are not generically applicable for all RNA systems or do not offer the required increase in computational efficiency.

Coarse-grain (CG) methodologies have emerged as an alternative solution to accelerate the conformational sampling and convergence. The drastic reduction in number of particles and interactions in CG models makes simulations of significantly larger systems possible (12, 13, 14, 15). Concerning CG models for RNA, existing models describe each RNA nucleotide with varying numbers of particles, depending on the specific purpose of the CG model. Some CG models for RNA are very coarse, and use just one (16, 17) or three (18, 19, 20, 21) pseudo-atoms or CG beads to describe each RNA nucleotide, following the pioneering work of Thirumalai and co-workers a decade ago (22). These highly simplified models have been created mainly for the prediction of 3D RNA structures, using experimental information as external constraints. More recently, less coarse models, like the HiRE-RNA from Pasquale and Derreumaux (23, 24, 25), the SimRNA model from Boniecki et al. (26), the oxRNA model from Šulc and co-workers (27), or the model of Ren and co-workers (28, 29), have been developed. These more detailed CG models show that the inclusion of higher resolution in the backbone and/or bases improves the overall behavior of RNA molecules, allowing realistic simulation of processes such as hybridization, supercoiling, and quadruplex formation.

Although many of the specialized RNA models are very good at what they were designed for, there is a clear need to develop a CG RNA model that can be incorporated into complex biological systems. To our knowledge, only the RNA model from Hori and Takada (19) is transferable to systems including other (nonnucleic acid) biomolecules. In addition, many of the aforementioned CG RNA models are implicit-solvent models, which limits the range of applications. Therefore, we have developed an RNA model within the Martini force field framework (30) that can be used in combination with other Martini models, such as the existing models for proteins (31, 32), DNA (33), carbohydrates (34), and lipids (35, 36, 37, 38, 39) at a wide range of solvent conditions.

In the Martini model, on average, four heavy atoms plus associated hydrogens are represented by a CG bead. Small ring-like fragments or molecules (e.g., the nucleobases) are mapped at higher resolution. The CG beads interact via standard interaction potentials for covalent bonds, bond angles and dihedral rotations, a Coulomb potential for charged sites (e.g., phosphate groups or ions), and a modified Lennard-Jones (LJ) potential for short-range van der Waals interactions. In the Martini DNA model (33), special LJ interactions are used to reproduce correct base-base stacking, and to mimic the relative strength of the basepairing. In the parameterization process of the Martini model, top-down and bottom-up approaches are combined. The main targets are experimental data like densities of liquids and transfer free energies of small solutes partitioning between polar and nonpolar solvents, which are used to determine nonbonded interaction parameters, and atomistic reference simulations, which are primarily used to extract bonded interaction parameters. A detailed description of the Martini force field can be found elsewhere (30).

Here, we developed the RNA parameters according to the general strategy for Martini parameterization, i.e., combining a top-down and bottom-up approach. The bead-type selection was done based on the Martini DNA model (33), aimed at reproducing experimental partitioning free energies. The bonded interactions were fitted to bond, angle, and dihedral distributions derived from state-of-the-art atomistic simulations of short single-stranded RNAs (ssRNAs). Our model uses an elastic network for keeping the tertiary structure of RNA and thus is not capable of folding RNA. Performance of the single-stranded and double-stranded RNA (ssRNA and dsRNA, respectively) CG models was tested with respect to all-atom models, focusing on local and global flexibility and ion-RNA interactions. Finally, we assessed the stability and reliability of the new RNA parameters in a number of protein-RNA complexes, including the ribosome.

Materials and Methods

Reference atomistic simulation protocol

A set of short ssRNA sequences (4-mers) was selected that included the GNRA, CUUG, and UNCG tetramers (where N and R stand for any nucleotide and any purine, respectively), which correspond to >70% of the hairpin loops commonly present in ribosomal and signal-recognition particle RNAs (40, 41). Initial structures were generated using the Nucleic Acids Builder module available in the AmberTools package (42). Besides the 4-mers, a set of other atomistic simulations was carried out to validate the CG RNA force field (see below).

In all cases, the structures were immersed in a box of water molecules and the minimal number of sodium ions necessary to neutralize the system. The starting structures were minimized, heated, and equilibrated for 1.1 ns by releasing the harmonic restraints applied to the RNA molecules to avoid any artifact during the system equilibration, as explained elsewhere (43). After full relaxation, MD production runs were performed in the NPT ensemble with pressure set to 1 bar and temperature to 300 K using the Berendsen temperature coupling scheme and isotropic scaling for the pressure and a relaxation time of 5 ps. Periodic boundary conditions and the particle-mesh Ewald algorithm (44, 45) were used to account for the long-range electrostatic effects. All bonds were constrained at their reference distances using the SHAKE algorithm (46), which allowed the use of a time step of 2 fs.

For the simulation of RNA molecules, we used the AMBER99 force field (47) in combination with the parmbsc0 (10) and the parmchiOL3 (48) corrections to improve the description of the α/γ backbone dihedral angles and the χ dihedral angle, respectively. For comparisons of RNA and DNA, ssDNA simulations of the corresponding sequences were performed. For the DNA systems, we used the recent parmbsc1 (49) correction for DNA, which includes the parmbsc0 and other corrections on the sugar puckering, ε, ζ, and χ dihedral angles. The TIP3P rigid model (50) was used for water and the parameters from Joung and Cheatham (51) for the sodium ions. All atomistic simulations were carried out using the pmemd module included in the AMBER 12.0 MD package (42).

CG simulation protocol

CG simulations of RNA were based on the Martini force field developed for DNA (33) which includes the tiny beads and special bead types for the hydrogen-bonding beads of nucleotide bases, as explained in Uusitalo et al. (33). The CG simulations used a shifted van der Waals potential with parameters $r_{\text{vdw}\_\text{shift}}=0.9\text{nm}$ and $r_{\text{vdw}}=1.2\text{nm}$ and a shifted Coulomb potential with an $r_{\text{c}}=1.2\text{nm}$ cutoff and the shift starting from 0 nm. The relative permittivity was set to ${\epsilon }_{\text{r}}=15$ and the neighbor list cutoff was $1.4\text{nm}$. This setup corresponds to the “common” set of parameters (52). Temperature was coupled to 310 K using the Berendsen thermostat (53) with time constant ${\tau }_{\text{T}}=2.0$ while the pressure was maintained near 1 bar using the Berendsen barostat (53) with time constant ${\tau }_{\text{p}}=3.0$ and compressibility of $3.0\times {10}^{-4}{\text{bar}}^{-1}$. Constraints were solved using the LINCS algorithm (54) with parameters $\text{lincs}\_\text{order}=8$ and $\text{lincs}\_\text{iter}=2$. All production runs were performed using a time step of $10\text{fs}$, although shorter time steps were used in equilibration.

To obtain the bonded parameters, a set of short ssRNA strands, listed in Table S1, was simulated with Martini and the distributions of the bonded terms were compared to the reference atomistic simulations. Each ssRNA was simulated in a dodecahedron box where the minimum distance between periodic images was no smaller than $2.5\text{nm}$ with ∼300 water beads and counterions. The CG bonded parameters were then adjusted to improve the overlap of the CG and reference distributions and the simulations were repeated with the new parameters. This process was iterated until a good correspondence between the CG and the atomistic distributions was found. Systems with the final parameters were simulated for 1 μs and the last $500\text{ns}$ were used for analysis.

For modeling dsRNA structures, both a stiff and a soft elastic network were used. For the stiff model, a $1.0\text{nm}$ cutoff and a $500\text{kJ}{\text{nm}}^{-2}$ force constant were used (all CG beads within a distance of 1.0 nm from each other are connected through a harmonic potential constraining their relative positions in the starting structure with the given force constant). For the soft model, a cutoff of 1.2 nm and a force constant of $13\text{kJ}{\text{nm}}^{-2}$ were used instead. The elastic network is required as the Martini model does not consider directional hydrogen bonding and follows the use of similar elastic networks in the Martini protein (55) and DNA (33) force fields. All CG simulations were performed with GROMACS 4.5 (56).

Test systems

To evaluate the performance of the Martini RNA model, several test systems were examined. The flexibility of single-strand molecules was studied by simulating polyU and polyT oligonucleotides with lengths varying from 10 to 40 bases at different NaCl concentrations (50, 200, and 800 mM). For comparison, the same systems were simulated at atomistic resolution. CG and atomistic simulations were run for 1 μs and 100 ns, respectively.

We also evaluated the structural stability and local flexibility properties of dsRNA structures. To this end, we used two dsRNA structures (PDB: 1RNA and 1QC0) and a DNA:RNA hybrid (PDB: 1FIX) to evaluate the behavior of the soft and the stiff models compared to atomistic MD simulations. CG simulations were run for 1 μs of simulation time and atomistic simulations were run for 100 ns.

The ion atmosphere around the Martini RNA was also examined. Ion distributions were obtained around the 1RNA dsRNA structure at $10,100$ and $1000\text{mM}$ NaCl concentrations with both the standard Martini water model and the polarizable water model (57). Simulations with the polarizable water used particle mesh Ewald (44, 45) for electrostatics and had a relative electric permittivity set to ${\epsilon }_{\text{r}}=2.5$. To minimize finite-size effects (58) in our calculations, we used a large simulation cubic cell employing a 190 Å box. CG simulations were run for 1 μs and atomistic simulations for 100 ns.

To test the structural stability of larger RNA and RNA/protein complexes, we selected six systems: an RNA-containing a long internal loop (PDB: 4FNJ) (59), a 14-mer cUUCGg tetraloop hairpin RNA (PDB: 2KOC) (60), the HuD protein bound to a short AU-rich ssRNA (PDB: 1FXL) (61), protein 19 of the human signal recognition particle (SRP19) in complex with helix 6 of the human SRP RNA (PDB: 1JID) (62), the SRP19 protein with the 7S.S RNA from the thermophilic methanogenic archaea (Methanocaldococcus jannaschii) (PDB: 1LNG) (63), and the Thermus thermophilus 70S ribosome (PDB: 4V42) (64). Each system was coarse-grained using the scripts martinize.py and martinize-nucleotide.py and subsequently solvated (water and 150 mM NaCl) and simulated for 100 ns at the CG Martini level using the same parameters as described above, i.e., including the stiff elastic network. For the protein structure, we used the ElNeDyn elastic network (55) that allows changes in the orientation of the secondary elements while keeping the secondary structure of the protein motifs. No intermolecular elastic network was applied between RNA and protein molecules. Nonbonded interactions between RNA and protein were calculated based on the Martini interaction matrix, which can be found in the original publication (36).

To assess the conformational stability of these systems, we backmapped the final configurations of the RNA and protein−RNA complexes (except for the ribosome) from the Martini CG scale to the AMBER all-atom scale using backward (65). After the resolution transformation, an equilibration run was done with initram.sh using the default settings (500 step energy minimizations followed by short MD simulations using 0.2, 0.5, 1.0, and 2.0 fs time steps) (65). Mapping files for the Martini RNA nucleotides were created according to AMBER and CHARMM atom definitions and based on the Martini to CHARMM DNA mapping files (33). The martinize-nucleotide.py script used to coarse-grain RNA and DNA structures is available at http://cgmartini.nl together with files for backmapping the CG structures to atomistic resolution.

Analysis details

To analyze the flexibility of the CG ssRNA, the radii of gyration and the end-to-end distances were calculated for polyU and polyT single-stranded oligonucleotides. The second half (500 ns) of the trajectories was used for analysis. For CG trajectories, we used the polystat tool included in the GROMACS 4.5 package, whereas the AMBER trajectories were analyzed using the cpptraj module included in the AmberTools package (42).

We calculated the helical parameters of dsRNA molecules with CURVES+ (66) for atomistic MD simulations. For CG RNA molecules, the helical descriptors were calculated using an in-house software tool cgHeliParm.py (based on the same reference frames as atomistic methods (67) and available at the http://cgmartini.nl website). We also calculated the persistence length of long dsDNA and dsRNA molecules. The persistence length was calculated using the time-averaged angle between the end-to-end vector of the polymer and the vector between the first two monomers, which is used as a reference (33, 68). The estimate for persistence length is obtained by placing the reference vector in 10 separate positions and fitting the equation to the averaged data (33). The errors are estimated as the standard deviation after doing block averaging with five blocks on the data.

The accumulation and depletion of ions around dsRNA was quantified by calculating the preferential interaction coefficients, Γ_i (where i is the ion) for Na⁺ and Cl⁻ ions. Using the formalism from Smith (69), the preferential interaction coefficient of a cosolute (either the cation or the anion) is calculated as follows:

$${\text{Γ}}_i=N_i-\frac{{\rho }_i}{{\rho }_{\text{water}}}{N}_{\text{water}},$$

where N_i denotes net excess or net deficit of cosolute particles, i, in a local region surrounding the dsRNA molecule compared to a homogeneous solution of the same volume without solute, and ρ_i corresponds to the density of particle i (58).

Results and Discussion

Mapping of RNA bases and backbone

In the standard Martini model, on average, four heavy atoms plus associated hydrogens are represented by a single CG bead (36). For ring-like fragments, a higher-resolution mapping is used. Based on the chemical nature of the underlying structure, the CG beads are assigned a specific particle type with more or less polar character. The Martini model has four main types of particle: polar (P), nonpolar (N), apolar (C), and charged (Q). Within each type, subtypes are distinguished either by a letter denoting the hydrogen-bonding capabilities (d, donor; a, acceptor; da, both; 0, none) or by a number indicating the degree of polarity (from 1 = low polarity to 5 = high polarity), giving a total of 18 particle types or “building blocks.” Nonbonded interactions are described by an LJ 12-6 potential. The strength of the interaction is determined by the value of the LJ well depth, ε, which depends on the interacting particle types. The effective size of the particles is governed by the LJ parameter σ = 0.47 nm for all normal particle types. For the special class of particles in ring-like molecules (denoted with prefix “S” for small), slightly reduced parameters are defined. In the case of DNA, another class of particles with σ = 0.32 nm (prefix “T” for tiny) has been introduced to allow for optimal base-base stacking. In addition, special bead types for the hydrogen-bonding particles of the nucleobases were introduced to mimic the relative strength of base-base pairing. The DNA bead types were optimized based on free energies of partitioning and dimerization free energies of the bases. For details, we refer to the publication of the original DNA model (33).

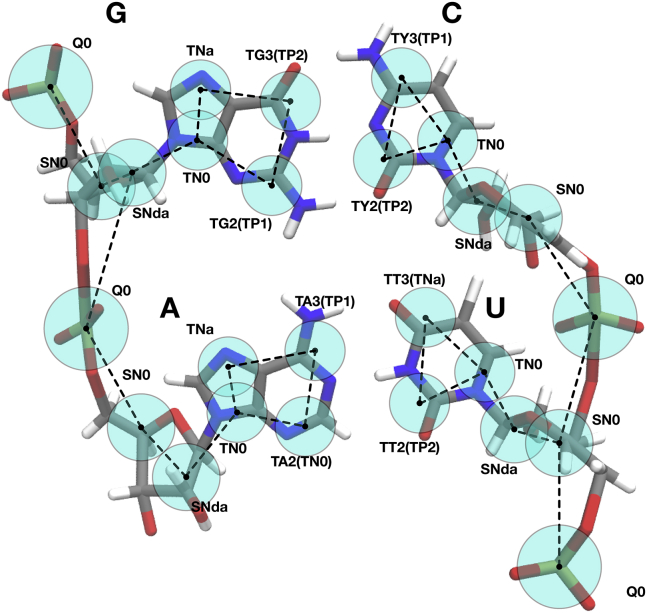
The mapping of the Martini RNA nucleotides closely follows that of the Martini DNA model. The complete mapping of RNA is shown in Fig. 1 (see also Table S2 for exact atoms-to-beads mappings). Compared to DNA, there are two important changes. First, the hydroxyl group in the ribose moves the position of the BB3 bead in RNA, and also the bead type is different; for RNA, BB3 is modeled as an $SNda$ bead type compared to $SC2$ in DNA. The choice of $SNda$ bead type reflects the more polar character of the ribose, as well as its hydrogen-bonding capabilities. Second, the uracil base is modeled with three beads that have the same bead types as thymine to retain its hydrogen-bond acceptor property; however, the position of the uracil SC3 bead is changed due to the methyl group that is not present in uracil but is part of thymine. The same bead-type names as in thymine are used for uracil to avoid unnecessary duplication of bead types in the topology.

Figure 1.

CG Martini mapping of RNA residues. The RNA backbone is modeled with one bead describing the phosphate (carrying a -e charge) and two beads describing the sugar. The pyrimidines are modeled with three beads and the purines with four beads. The Martini bead type of each bead is shown; the S- or T-prefix marks the beads that use the small/tiny bead type. For the basepairing beads, the special hydrogen-bonding bead types are shown together with the bead type describing their interactions with all other beads (in parentheses). Compared to DNA, the bead type and position of the backbone bead BB3 (type SNda) and the position of SC3 (type TT3) in uracil have changed. Uracil uses the same TT-type hydrogen-bonding beads as thymine since their parameters are the same, and addition of a TU-type would unnecessarily complicate the topology files. To see this figure in color, go online.

Optimization of bonded parameters

Bonded interactions in Martini are typically obtained from reference atomistic simulations of the target molecules in solvents representative of their natural surrounding (36). For the DNA model, the bonded interactions were fitted to reproduce bond, angle, and dihedral distributions obtained from atomistic simulations of short ssDNAs in aqueous environment (33). The bonded parameters are optimized using an iterative procedure described in Materials and Methods.

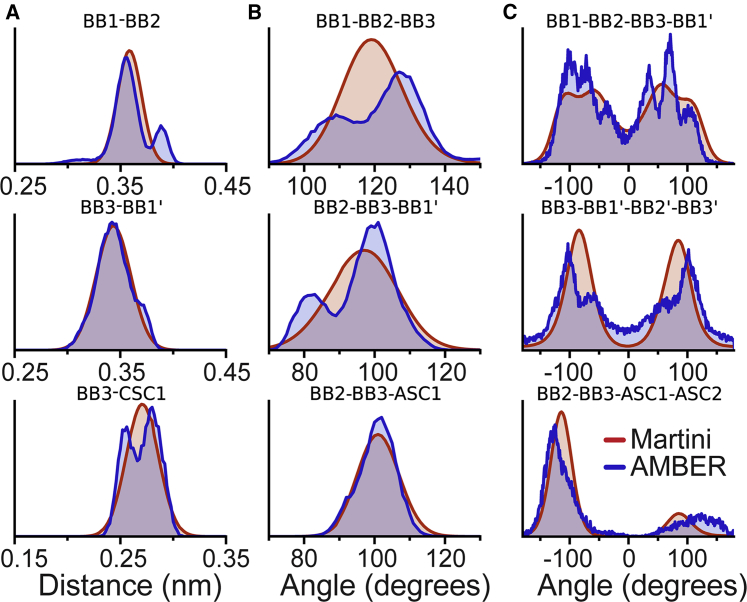
The bonded parameters of RNA necessarily differ from those of DNA, since the differences in atomistic structure shift the positions of the CG beads and change the flexibility of the molecule. Fig. 2 shows examples of the correspondence between the CG distributions obtained using the final CG parameters and the reference atomistic simulations of a set of short (four bases) ssRNA fragments (Table S1). A full list of all the distributions can be found in Fig. S1. The CG distributions match the atomistic distributions well, although with less detailed surfaces. The main target, that similar regions of the distance or angle space are sampled with comparable probabilities, is achieved well. Some compromises had to be made in the accuracy of the dihedral distributions to avoid stability issues that arise in Martini when an angle that is part of a dihedral can reach $180°$. For a more complete explanation of this issue, see Bulacu et al. (70). The improved angle potential of Bulacu et al. (70) was, however, not used for RNA to make sure the model is compatible with simulation codes other than GROMACS 5 (71). The full parameter set for Martini RNA is presented in Table S3.

Figure 2.

Validation of bonded interactions. Example comparisons of bonded distributions from atomistic AMBER simulations (trajectories mapped to CG resolution to calculate the distributions), shown in blue, and from CG Martini simulations, shown in red. (A) Three different bond distributions are shown. (B and C) Three angle distributions (B) and three dihedral distributions (C) are shown. The beads from the following residue are marked with an apostrophe. For a comparison of AA versus CG distributions for all bonded terms, see Fig. S1. To see this figure in color, go online.

Validating the ssRNA model

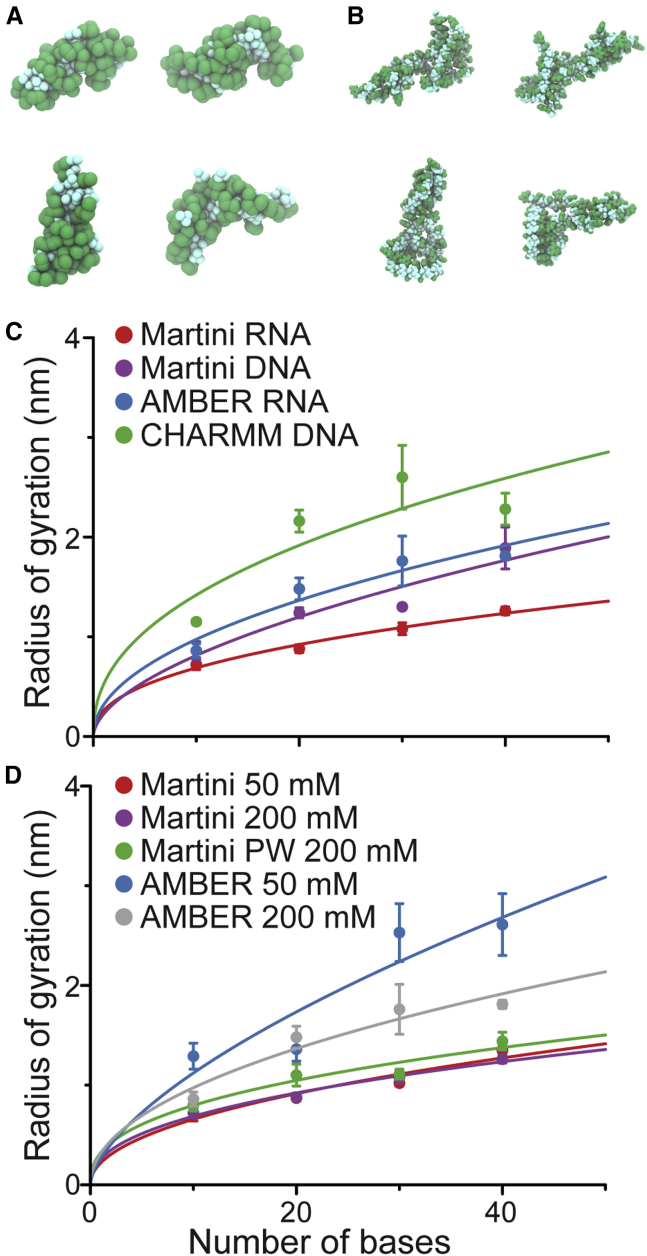
As a first test of the RNA model, we studied the flexibility of ssRNA by calculating the radius of gyration of ssRNAs of varying lengths consisting solely of uracil bases. We compared these results with atomistic simulations of the same systems. We also studied the differences with ssDNA by simulating polyT strands both at CG and at atomistic resolutions. The results, which are presented in Fig. 3, show that the CG model predicts a lower radius of gyration for both ssRNA and ssDNA. Interestingly, for both atomistic and CG simulations, ssRNAs have a smaller radius of gyration than their ssDNA counterparts. However, single-molecule Förster resonance energy transfer (smFRET) measurements of 40-base-long polyT and polyU strands point to an opposite behavior (72). These results indicate that the computational models are consistent with each other in behavior but contradict the experimentally observed behavior. Visual inspection of the simulations confirmed that CG strands form tighter structures compared to the atomistic models (see Fig. 3, A and B). In interpreting these results, though, a word of caution regarding the difference in sampling times: 1 μs of CG simulations compared to $150\text{ns}$ of atomistic simulations. Nevertheless, the RNA Martini model appears to be somewhat softer than the atomistic model.

Figure 3.

Flexibility of ssRNA. Differently long single-stranded polyU RNAs and polyT DNAs were simulated at both the atomistic (AMBER or CHARMM) and CG Martini levels and their flexibility assessed. Representative snapshots from 40-bp long polyU RNA simulations with Martini (A) and AMBER (B) are shown. The radius of gyration was compared between RNA and DNA at 200 mM NaCl concentration (C) and ionic strength dependence of ssRNA is shown (D). The lines are a fit to the measurements to clarify the differences between the models. The error bars show the standard deviation of the measured values. To see this figure in color, go online.

Furthermore, we explored the effect of NaCl concentration on the flexibility properties of ssRNAs. We measured both the radius of gyration and the end-to-end distances for polyT and polyU sequences of 40 nucleotides long in 50, 200, and 800 mM NaCl solutions. It is expected that the increase of cations reduces the repulsion along the negatively charged backbone, favoring the formation of more compact conformations. Contrary to atomistic simulations and previous experimental data (72), however, the end-to-end distance values for CG ssRNA molecules (Fig. S2) do not exhibit a clear dependence on the NaCl concentration. This behavior was already observed in the previous Martini DNA work (33) and was therefore expected for the Martini RNA model. As for the Martini DNA model, the use of the more accurate polarizable water slightly improved the treatment of electrostatics in Martini at increased salt concentration (Fig. 3 D).

Validation of dsRNA

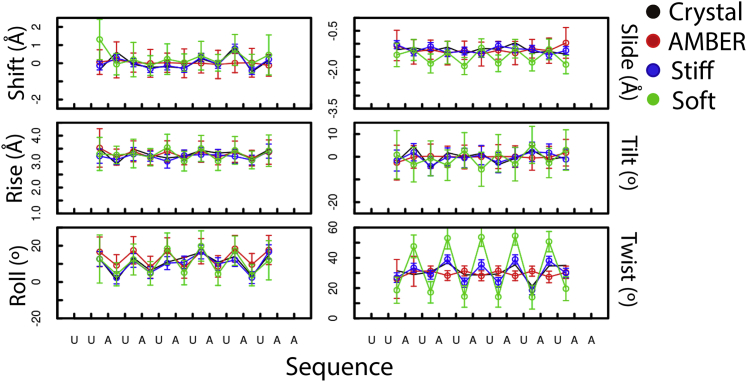
To determine how well Martini RNA retains the dsRNA structural characteristics, we simulated three dsRNA x-ray structures (73, 74, 75) using both soft and stiff elastic networks (see Materials and Methods). To assess the stability at the basepair level, we compared the helical parameters (76) with the values obtained from the initial crystal structures as well as in atomistic simulations. As an example, the calculated values for the 6 bp step helical parameters for PDB: 1RNA (73) are shown in Fig. 4 (results for PDB: 1FIX and 1QC0 are shown in Figs. S3 and S4, respectively). As expected of an elastic network, the helical parameters for the Martini RNA model show that the original structure of the dsRNA is closely maintained. Both soft and stiff elastic networks follow similar values, but the soft model shows higher local flexibility (bigger standard deviations) than the stiff model. The atomistic model also tracks closely the crystal structure, behaving similarly to the soft model.

Figure 4.

Basepair-step helical parameters. Values obtained from 100 ns simulation of a PDB: 1RNA dsRNA molecule in 150 mM NaCl. The values from the crystal structure are in black, atomistic AMBER simulations in red, stiff RNA Martini model in blue, and soft RNA Martini model in green. To see this figure in color, go online.

As we did for the Martini DNA model, we paid particular attention to validate the Martini RNA model in terms of the mechanical properties. We considered that one duplex is more flexible than another when the persistence length is lower. We previously showed that the Martini DNA model is able to replicate the experimental persistence length at physiological ion concentration (150 mM NaCl) (33). Under the same conditions, the experimental persistence length values for dsDNA are ∼45–50 nm (77, 78) whereas for dsRNA they are between 58 and 80 nm (79, 80). To measure the persistence length, we simulated two double-stranded molecules (dsDNA and dsRNA) of 100 bp length of a random sequence (Table S4) at the CG resolution. The simulations were run using the stiff and the soft models for 1 μs. The analysis of the persistence length values for molecules of the same sequence (changing T to U in the dsRNA) showed that dsDNA is more flexible than dsRNA (Table 1). The persistence length values for dsDNA and dsRNA with the soft model were ∼50 ± 6 nm and ∼62 ± 10 nm. Although our results are restricted to a single sequence, they are in agreement not only with experimental results of longer sequences but also with previous theoretical calculations (81).

Table 1.

Persistence Length Values of dsDNA and dsRNA

	Persistence Length (Soft) (nm)	Persistence Length (Stiff) (nm)
dsDNA	50 ± 6	206 ± 53
dsRNA	62 ± 10	208 ± 52

Comparison of the values obtained using the soft and the stiff CG models for 100-bp-long dsDNA and dsRNA. The sequence is included in Table S4.

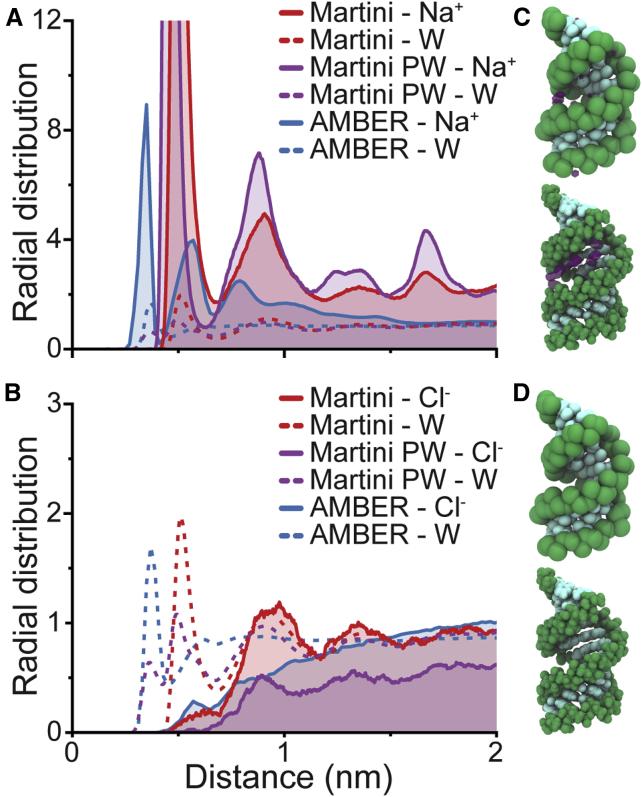
The interaction of ions with DNA and RNA critically affects biological and physical processes. The negatively charged backbone of nucleic acids leads to condensation of positive ions from solution. To test how well the Martini RNA model describes these interactions, we studied the ion distributions around the PDB: 1RNA dsRNA molecule at 10, 100, and 1000 mM NaCl solutions and compared those to ion distributions from atomistic simulations. Given the implicit electrostatic screening of the standard Martini water model, we also tested the polarizable water model. The results with $100\text{mM}$ NaCl solution are presented in Fig. 5, and the higher ion concentration results are presented in Fig. S5. The radial distribution functions (RDFs) of ions around RNA phosphates showed a slightly higher sodium concentration around the CG model compared with the atomistic simulations. The overall location and periodicity was similar and well captured but shifted 0.1–0.15 nm, as the atomistic sodium ions are able to approach closer to the phosphates. This is expected because of the larger size of the CG beads that prevent the access of ions and water closer than 0.5 nm to the CG RNA model. On the other hand, chloride ions were only visible after the first solvation shell of the RNA molecule in both atomistic and coarse-grain simulations. The chloride ions were thus expelled from the first solvation shell but sensed no strong effect of the DNA beyond the first shell. The screening effect was reduced with polarizable water and PME (Fig. S5), bringing the atomistic and CG results into closer agreement. If compared to the results obtained with the DNA model in Uusitalo et al. (33), ion behavior around the RNA model is consistent with those results.

Figure 5.

Ion distribution around dsRNA. A comparison of sodium (A) and chloride (B) RDFs around RNA phosphates in 100 mM NaCl. The atomistic RDF is shown in blue, Martini with standard water in red, and Martini with polarizable water in purple. Dashed lines present the water RDF as a reference. Snapshots including the most commonly occupied volume for sodium (C) and chloride (D) ions around the RNA structure are shown in CG (top) and in an atomistic simulation (bottom). The snapshots of CG systems are from simulations with standard Martini water. Ion distributions from simulations with 1000 mM NaCl are shown in Fig. S5. To see this figure in color, go online.

In addition to the specific binding of ions to the RNA, the presence of a less site-specific ion atmosphere around nucleic acids is well established (82, 83, 84). For decades, a major challenge was the lack of rigorous experimental data to characterize the ion environment. In the last decade, direct quantification of ions associated with DNA and RNA has been possible by using buffer equilibration atomic emission spectroscopy (BE-AES) measurements (82). Experimental data have shown that counterions locate in a smaller volume around the DNA or RNA and that the local environment together with the macroion is charge neutral (82). Comparisons with experimental data have shown that MD simulations provide a faithful representation of the local atmosphere (85). In these calculations, the accumulation of counterions and the depletion of coions around nucleic acids can be quantified using the preferential interaction coefficients, Γ_i (see Materials and Methods). We measured the coefficients for Na⁺ and Cl⁻ ions for a wide range of concentrations (10, 100, and 1000 mM). As shown in Fig. 5, Na⁺ ions accumulate preferentially around RNA phosphate groups, whereas Cl⁻ ions are depleted. This leads to positive values of Γ₊ and negative values of Γ₋ (see Table 2). We also note that the change in the number of ions associated is small over the wide range of concentrations studied. This is expected given the fixed number of phosphate groups in the RNA molecule. However, previous BE-AES measurements showed that there is a systematic decrease of the number of Na⁺ ions and a corresponding increase of Cl⁻ ions as the bulk ion concentration increases (82). From our simulations, this is unclear, since the values at 1000 mM NaCl solution have a big error associated. In addition, the total charge of the ion atmosphere showed that the associated Na⁺ ions plus the excluded anions (Γ₊ + |Γ₋| in Table 2) compensated the net charge of the RNA molecule within error (RNA charge is −26e) for concentrations ≥100 mM. Electroneutrality was not achieved in our calculations in 10 mM NaCl solution, but this is consistent with previous experimental and all-atom MD studies (86).

Table 2.

Values of Preferential Interaction Coefficients for Na⁺ and Cl⁻ Ions around the PDB: 1RNA Structure in Different NaCl Concentrations

NaCl Concentration (mM)	Γ+	Γ−	Γ+ + |Γ−|
10	15.8 ± 2.0	−1.0 ± 0.8	16.9 ± 2.1
100	19.8 ± 3.1	−3.9 ± 2.9	23.9 ± 3.0
1000	20.8 ± 7.5	−4.4 ± 7.4	27.9 ± 7.0

Values averaged over the last 200 ns of 1 μs simulation time. The local region around the RNA was defined as a sphere of 4 nm radius. The radius was chosen according to the RDF analysis (Fig. S6).

RNA tertiary stability and RNA-protein interactions

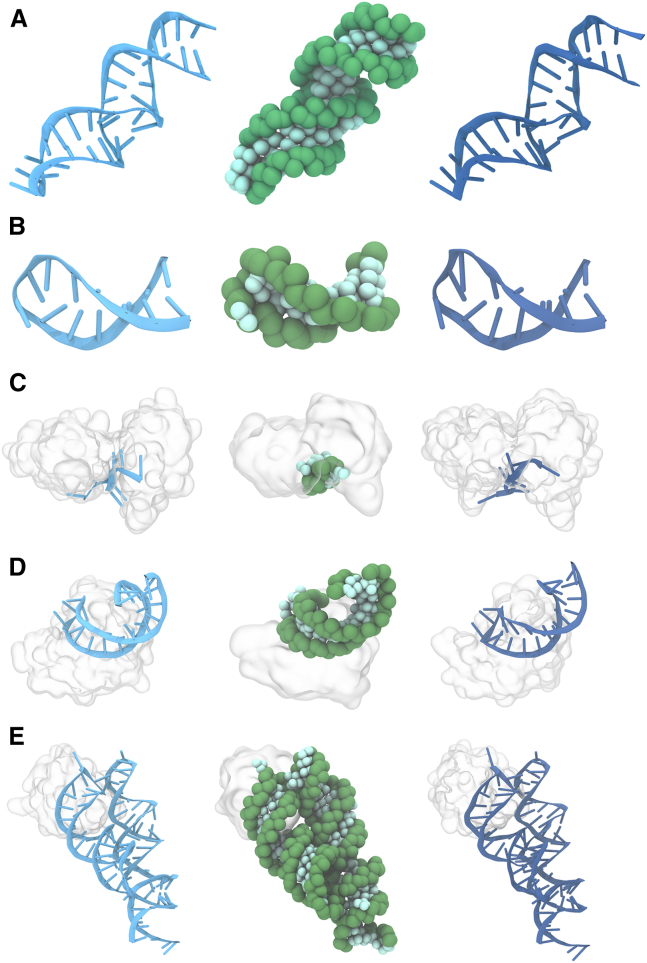
We studied the ability of the Martini RNA model to describe tertiary RNA structures and RNA-protein interactions using six example systems as test cases. The systems studied were a 14-mer cUUCGg tetraloop hairpin RNA, an RNA containing a long internal loop, the HuD protein bound to a short AU-rich single stranded RNA, protein 19 of the human signal recognition particle (SRP19) in a complex with helix 6 of the human SRP RNA, the SRP19 protein with the 7S.S RNA from the thermophilic methanogenic archaea (M. jannaschii) and the bacterial (T. thermophilus) 70S ribosome. The first two systems were chosen since they contain common RNA motifs such as apical and internal loops. Despite the stiff elastic network applied around the loop residues, the differences in flexibility between the helix and the loop motifs were visible and agree reasonably with atomistic simulations (Fig. S7). The remaining systems represent only a small part of the large pool of RNA-protein complexes in structural databases. In all cases, the final CG structures remained close to both the atomistic and crystal structures, implying that the CG RNA model performed well in terms of stability (Fig. 6). In addition, the RNA-protein complexes stay bound to each other during the simulations showing that the Martini model can be straightforwardly used to study RNA in complex with other biomolecules.

Figure 6.

RNA and protein/RNA stability. Shown are the starting configuration, i.e., crystal structure (left), the final CG configuration (middle), and the atomistic structure obtained after backmapping (right). Studied systems were PDB: 4FNJ (59) (A), 2KOC (60) (B), 1FXL (93) (C), 1JID (62) (D), and 1LNG (63) (E). To see this figure in color, go online.

The simulation of the ribosome is a further proof of concept that big complexes involving multiple RNA strands and proteins can be straightforwardly simulated using the new Martini model. The final snapshot of the complex, after 100 ns of simulation performed overnight on a local desktop machine, is shown in Fig. 7.

Figure 7.

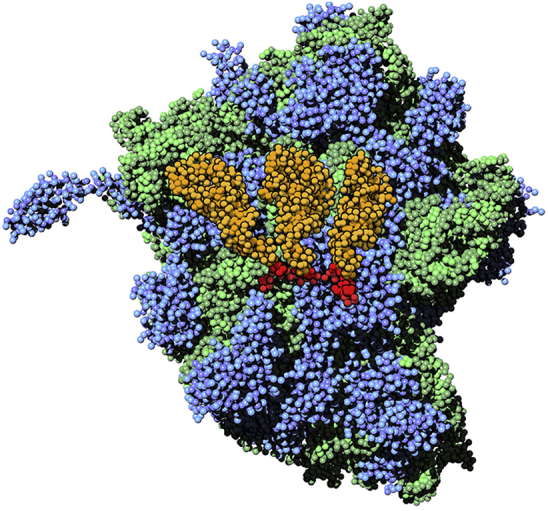
The Martini ribosome. Martini CG structure of the ribosome (PDB: 4V42) after 100 ns of simulation using the stiff elastic network for the RNAs and ElneDyn (55) for the proteins. RNAs of the ribosome complex are in green and the protein molecules are in blue. In the center, messenger RNA (red) and the three transfer RNAs (orange) are highlighted. To see this figure in color, go online.

To provide insights into the ability of our Martini RNA model to predict the formation of protein/RNA complexes, we have performed additional simulations on the RNA-protein systems in Fig. 6, D and E with the protein and the RNA molecules initially separated by 1 nm. In these simulations, we observed reassociation after a few nanoseconds, but only a limited fraction of the native interactions was actually recovered (see Fig. S8). We believe that by extending the simulations (currently 1 μs) we could increase the number of native interactions, but rearrangements in the bound state are slow, and full recovery of the final complex might require several microseconds. To investigate this in more detail, a high-throughput association study should be performed, with enhanced sampling methods. That is beyond the scope of this study, but certainly of interest for future work.

Limitations of the Martini RNA model

For proper use of the Martini RNA model, it is important to discuss the limitations. Three of the key limitations of the Martini model, inherent to the loss of resolution, are relevant to the RNA model as well. The first generic limitation is the entropy-enthalpy compensation, due to the replacement of entropic degrees of freedom by effective pairwise interactions. Because of this, care has to be taken when considering the driving forces of processes, or the temperature dependency. Second, due to missing atomic interactions, the potential energy landscape is smoothened and the system dynamics becomes artificially enhanced. The timescale should therefore be considered as qualitative only. Third, because of the reliance of Martini on an atomistic force field for parameterization of the bonded interaction terms, any inaccuracies of the atomistic force fields are inherited. In case of RNA, atomistic force fields are still considered to be problematic and in need of improvement (5).

Furthermore, our RNA model shares two of the main limitations of the DNA model: 1) the reduced strength of the base-pairing interactions due to the inability of Martini to model directional hydrogen bonds, and 2) the use of an elastic network to constrain the RNA structural arrangement. Consequently, Martini RNA cannot be used to study RNA hybridization, melting, hairpin formation, or intercalation. The explicit solvent limits some applications that require length- and timescales that can be achieved only with even faster implicit-solvent models that have drastically fewer degrees of freedom.

We foresee the model to be used mostly in intermolecular applications where RNA plays its own role in a complex environment composed of other biomolecules such as RNA−RNA interactions between long-noncoding RNAs, RNA-protein interactions as in the ribosome, and RNA-lipid interactions in RNA viruses and within drug-delivery systems for antisense therapies or in other nanotechnology applications.

Conclusions

We developed a model for RNA that is compatible with the Martini force field. We followed the same parameterization methodology used for other Martini molecules and specifically the same procedures as for the recent Martini DNA model (33). The mapping of RNA was made as similar as possible to the mapping of the DNA model while making the differences between RNA and DNA visible in both bead-type assignment and position of CG beads. The bonded interactions were parameterized against atomistic reference simulations performed with the AMBER99 force field, including the latest modifications for RNA molecules (10, 47, 48).

The CG RNA model was tested for both in ssRNA and dsRNA forms. The flexibility of ssRNA was compared to both atomistic reference simulations and to ssDNA. The CG ssRNA was found to be softer than the CG ssDNA model while both models were softer than their reference atomistic simulations. The dsRNA was tested with two modes; featuring a soft or a stiff elastic network. The stiff model showed a significantly higher persistence length compared to experimental numbers. This is in line with the main purpose of the stiff elastic network, which is to closely retain RNA tertiary structure. Consequently, the dsRNA model was found to reproduce well the helical parameters of dsRNA molecules with small variation in the helical parameters. The soft model showed agreement with the generally accepted experimental persistence length for dsRNA molecules and its relative value compared to DNA molecules. The ion distributions around dsRNA were found to compare favorably with atomistic reference distributions, with small packing differences arising from the larger size of CG ions. The preferential interaction coefficients from large-size simulation boxes showed also good agreement with experimental data on ion atmosphere around nucleic acids. Finally, the RNA model was used to simulate RNA-protein structures, which were successfully backmapped afterward to atomistic resolution, allowing simulation of such systems across different resolutions depending on the required level of detail.

Although the stability of the RNA model is improved from the DNA model, the recommended maximum time step is still 10 fs, and smaller time steps are sometimes necessary. This, together with improved base-base interactions will be a major target for the next-generation Martini DNA and RNA model development. Another major target will be improving the ssRNA flexibility based on the radius-of-gyration results.

With the Martini RNA model, all major classes of biomolecules are now represented in the Martini force field. This opens up numerous possibilities for CG simulations, as demonstrated by recent applications of our nucleotide force fields in complex biological settings (87, 88, 89). The ease of backmapping the Martini model to atomistic resolution furthermore allows its use in various hybrid multiscale setups (90, 91, 92).

Author Contributions

J.J.U., I.F., H.I.I., and S.J.M. designed the research and wrote the manuscript. J.J.U. and I.F. performed the parameter development and J.J.U., I.F., and H.I.I. performed the validation and analysis.

Editor: Tamar Schlick.