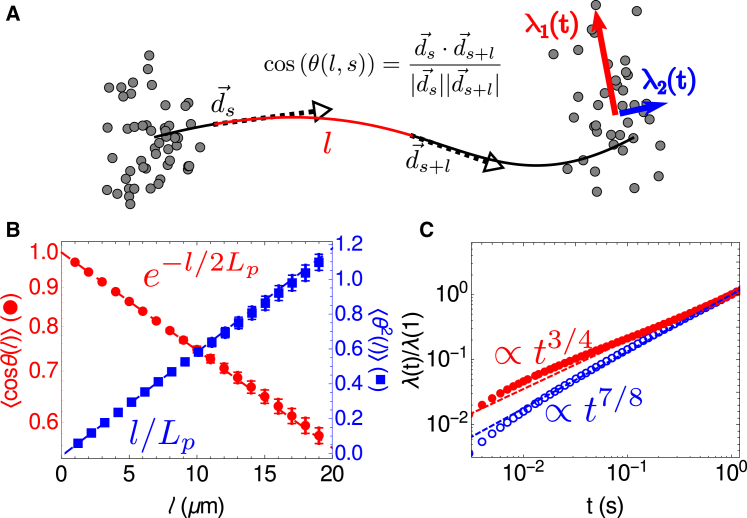
Figure 3.

Spatial and temporal fluctuations of the bead-spring WLC. (A) Shown here is a schematic of a filament and the order parameters that characterize its fluctuations. Spatial fluctuations are characterized by the angle between two tangent vectors ${\overrightarrow{d}}_s$ and ${\overrightarrow{d}}_{s+l}$ along the filament as a function of the contour length between them, l. Temporal fluctuations are characterized by the eigenvalues λ_1,2(t) of the covariance matrix of filament endpoint positions as a function of time. The red arrow indicates the larger moment (λ₁, measuring transverse fluctuations) whereas the blue arrow indicates the smaller moment (λ₂, measuring longitudinal fluctuations). (B) Given here is the decorrelation of tangent vectors (red circles) and fluctuations in angles between links (blue squares) as a function of the arc length between them. For the N = 20 filaments analyzed, the red circles (blue squares) show the mean of 〈cos(θ(l))〉 (〈θ(l)²〉) and the error bars show their standard errors, $\sigma /\sqrt{N}$, where σ is their SD. Dashed lines show expected behavior for κ_B = 0.068 pNμm². (C) Given here are eigenvalues of covariance matrices for the positions of endpoints of filaments as a function of time. Red filled circles show λ₁(t), which is expected to be proportional to t^3/4 (red line) whereas blue open circles show λ₂(t), which is expected to be proportional to t^7/8 (blue line). SE is smaller than the size of the data points. To see this figure in color, go online.