Translational Modeling to Guide Study Design and Dose Choice in Obesity Exemplified by AZD1979, a Melanin‐concentrating Hormone Receptor 1 Antagonist

Abstract

In this study, we present the translational modeling used in the discovery of AZD1979, a melanin‐concentrating hormone receptor 1 (MCHr1) antagonist aimed for treatment of obesity. The model quantitatively connects the relevant biomarkers and thereby closes the scaling path from rodent to man, as well as from dose to effect level. The complexity of individual modeling steps depends on the quality and quantity of data as well as the prior information; from semimechanistic body‐composition models to standard linear regression. Key predictions are obtained by standard forward simulation (e.g., predicting effect from exposure), as well as non‐parametric input estimation (e.g., predicting energy intake from longitudinal body‐weight data), across species. The work illustrates how modeling integrates data from several species, fills critical gaps between biomarkers, and supports experimental design and human dose‐prediction. We believe this approach can be of general interest for translation in the obesity field, and might inspire translational reasoning more broadly.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Quantitative relationships between obesity biomarkers are generally scarce in the literature. One exception is emerging semimechanistic body‐composition models. MCHr1 antagonists are well known to decrease body weight in rodents but very limited clinical data are reported.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ How can reported body‐composition models together with biomarker data from cells, animals, and humans guide study design and dose prediction for an MCHr1 antagonist?

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ The study specifically reports the quantitative relationships between MCHr1 antagonist biomarkers, how nonparametric input estimation infers energy‐intake trajectories from longitudinal body‐weight observations using a body‐composition model, and more generally how data from various sources can be integrated using different modeling techniques across species.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ The translational reasoning might be directly applicable to other drug‐discovery programs on MCHr1 antagonists or metabolic‐syndrome targets, and might more broadly inspire modeling efforts in drug‐discovery programs across disease areas.

Key modeling tasks in preclinical drug discovery are to predict the human pharmacokinetics (PKs) and pharmacodynamics (PDs), as well as the human dose. These predictions are essential for compound selection, cost‐of‐goods estimation, design of early clinical studies, and safety assessment. Typically, the preclinical modelers integrate in vitro cellular, animal, and potential human data, as well as literature data for relevant in‐house or competitor compounds into a mathematical model that predicts temporal profiles of key biomarkers and endpoints. Important means to advance this research field of translational modeling are to present general strategies1, 2, 3, 4 and to share specific examples.5, 6, 7, 8 This contribution belongs to the second category.

Our main objective is to present the translational reasoning used in the preclinical drug‐discovery program of AZD1979, a novel potent small molecule melanin‐concentrating hormone receptor 1 (MCHr1) antagonist.9 AZD1979 binds to MCHr1 in the central nervous system and affects energy intake (EI) leading to body weight (BW) loss in diet‐induced obese mice as well as in dogs.10 Dogs and humans, in contrast with rodents, express two melanin‐concentrating hormone receptors (MCHrs; MCHr1 and MCHr2). Except for desire‐to‐eat questionnaire data from one study,11 very limited clinical data are reported on MCHr1 antagonists,12 and, therefore, prediction to man is challenging. The preclinical data package9, 10 gave support for clinical testing as a candidate drug for the treatment of obesity and its comorbidities, but the study was terminated after the study‐stopping criteria relating to safety were reached (ClinicalTrials.gov Identifier: NCT02072993).

In our analysis, a causal map of the observed biomarkers formed the basis for translational reasoning (Figure 1).13, 14 The PK/PD model mirrors this map and quantitatively relates the biomarkers. Specifically, the PK/PD model contains the following main variables: dose, drug exposure, receptor occupancy (RO), target activation, EI, and BW. The complexity of individual steps of the translational model differs, and depends on the quality and quantity of available data as well as prior information. On the one extreme, semimechanistic body‐composition models available for rodents15, 16, 17 and humans,18, 19 were used to connect EI and body composition. Here, clinical data collected from obesity drugs targeting other receptors than the MCHr1 were used to inform about the human model. On the other extreme, simple linear regression was used to connect RO and EI.

Figure 1.

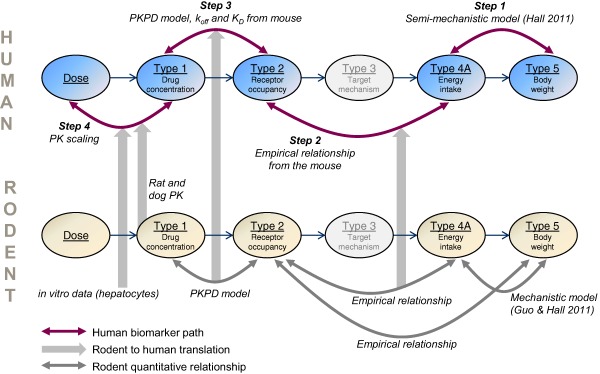
Key components of the pharmacokinetic/pharmacodynamic (PK/PD) model and scaling path. The human biomarker path is indicated by purple arrows, the rodent to human translation is indicated by thick gray arrows, and supporting quantitative relationships in rodents are depicted by gray arrows. Steps 1–4 include both empirical and mechanistic models. Target‐mechanism data were lacking in the melanin‐concentrating hormone receptor 1 program, and this is indicated by the gray color of that biomarker.

This biomarker‐centered approach allows for easy integration of human, animal, and cell‐assay data into one framework. When a relationship between two human biomarkers is missing, the data gap is filled with complementary data from cell assays and animal experiments. In addition, data from other MCHr1 antagonists than AZD1979 are occasionally used to support translation. Traditional forward simulation is complemented with input estimation (commonly referred to as deconvolution for linear systems). In this way, a biomarker (e.g., EI) that causally precedes another biomarker (e.g., BW) can be estimated from the dependent biomarker if a mathematical model that bridges the two biomarkers is available.

The paper is divided into four parts; each describing a fundamental modeling task along the causal pathway that drives AZD1979‐induced body‐composition changes (denoted by steps 1–4 in Figure 1). Throughout this analysis, each modeling step is thoroughly described and supported by literature findings or experimental data, or both.

METHODS

Considered melanin‐concentrating hormone receptor 1 antagonists

Besides AZD1979, data from the following MCHr1 antagonists were used in the analyses: example 88 (analogue to AZD1979; AstraZeneca) in patent WO2012/004588, here referred to as compound 88; compound 99 (analogue to AZD1979; AstraZeneca)9 and ALB‐127158(a) (Albany Molecular Research Inc.),11 here referred to as ALB.

Step 1. Predicting energy intake in human by nonparametric input estimation

Input estimation recovers the form of an input function, which cannot be directly observed. Step 1 recovers EI profiles from BW observations (Figure 2).

Figure 2.

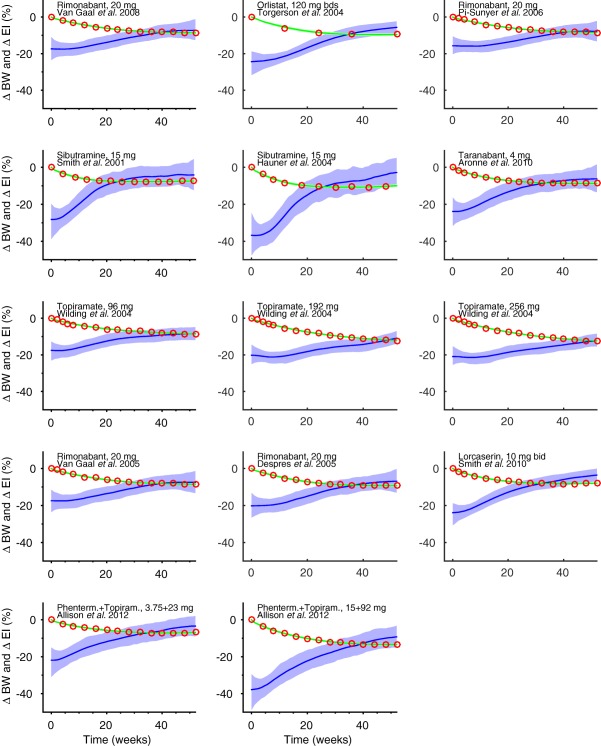
Body weight (BW) to energy intake (EI) in humans (step 1). BW data (red circles) from 14 key studies with rimonabant, orlistat, sibutramine, taranabant, topiramate, lorcaserin, and phentermine. During treatment, BW decreases initially but then tends to plateau. Plausible reasons include compensatory mechanisms increasing appetite, low compliance, or drug tolerance development, or a combination of those. Nonparametric input‐estimation was used to predict EI (blue line) by regressing Hall's body‐composition model on BW observations. The predicted EI drops initially and then returns to a level close to the initial baseline. The predicted BW curves are indicated by green lines. A 1% (peak) drug‐induced energy‐expenditure effect was assumed. The shaded areas are 95% credible intervals of EI and BW.

Average data from 14 clinical obesity studies20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 were retrieved from the literature and data were digitized. The following inclusion criteria were applied: studies with <30% of patients with diabetes; not using a very low‐calorie diet; BW decrease >7%; >4 sampled time‐points; the first sampling point before week 10; the second sampling point before week 26; and the last sampling point after week 51. The main mechanism of actions of the considered drugs is reduced EI.31, 32 For lorcaserin, there is even direct evidence that energy expenditure (EE) is not influenced.33 Therefore, <1% drug‐induced effect of EE was assumed.

A five‐state (lean tissue, body fat, glycogen, extracellular fluid, and adaptive thermogenesis) human body‐composition model, that takes EE adaptations during weight loss into account, was used to model BW data.18 Temporal EI was estimated using a nonparametric method (Supplementary Text).34 To elucidate the typical form of EI and BW time‐profiles resulting in 10% BW decrease after 1 year of treatment, the measurements from the literature were shifted (BW measurement at $t=0$ unchanged, whereas other measurements were shifted proportionally to time) so that they would reach 10% after 1 year, and EI was re‐estimated. The resulting curves gave an idea of the range of curvatures one could expect in clinical studies reaching 10% BW reduction in 1 year. First, data from only the active arms were analyzed, and then placebo‐corrected data were analyzed in the same way.

Step 2. Body weight, energy intake, and receptor occupancy in rodents

To quantitatively explore translation of EI and BW between rodents and humans, time‐series of EI and BW, or at least BW, in rodents upon treatment with the drugs considered in step 1 were retrieved from the literature and digitized (Figure 3 a–c). Specifically, data on EI and BW in the mouse are reported for rimonabant 10 mg/kg/day,35 sibutramine 10 mg/kg/day,36 and topiramate 66 mg/kg/day (only BW; Figure 3 a,c). Data on EI and BW in the rat are reported for rimonabant 10 mg/kg/day,37 taranabant 3 mg/kg/day,37 sibutramine 5 mg/kg/day,38 and lorcaserin 4 mg/kg/day39 (Figure 3 b,d).

Figure 3.

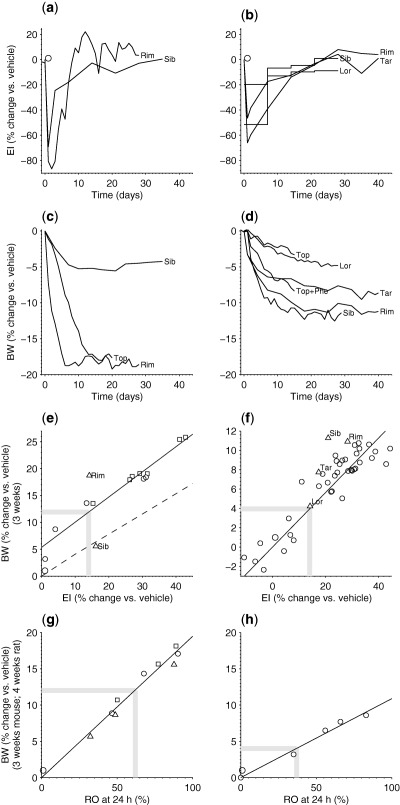
Energy intake (EI) to receptor occupancy (RO) in rodents (step 2). The left column shows data for the mouse and the right column shows data for the rat. (a) Mouse EI and (c) body weight (BW) data for rimonabant (Rim) 10 mg/kg/day, and sibutramine (Sib) 10 mg/kg/day. Mouse BW data for topiramate (Top) was 66 mg/kg/day. (b) Rat EI and (d) BW data for Rim 10 mg/kg/day, taranabant (Tar) 3 mg/kg/day, Sib 5 mg/kg/day, and lorcaserin (Lor) 4 mg/kg/day. (e) BW reduction vs. EI reduction in the mouse. AZD1979 observations (squares = female and circles = males) indicate a linear relationship (solid line). The triangles indicate corresponding data for Rim and Sib. The model15, 16 prediction (dashed line) is based on the assumption that the drug mainly targets EI and not energy expenditure. The parallel shift indicates a minor effect of AZD1979 on energy expenditure. (f) BW reduction vs. EI reduction in the rat. AZD1979 observations (circles) indicate a linear relationship (solid line). The triangles denote corresponding data for Lor, Tar, Sib, and Rim. (g) BW reduction vs. RO at 24 h in the mouse. Data for AZD1979 and other compounds of the same chemical series indicate a linear relationship (circles represent AZD1979, squares represent compound 99, and triangles represent compound 88). (h) BW reduction vs. RO at 24 h in the rat. Data from the melanin‐concentrating hormone receptor 1 antagonist ALB indicate a linear relationship as for the mouse. (e–h) The thick gray lines indicate the point estimates that give the RO‐to‐EI relationships, one for the mouse and one for the rat.

For AZD1979, the relationship between BW and EI reduction in the mouse was inferred from data collected from the control group of wild‐type mice in an MCHr1 knock‐out study.10 The mouse body‐composition model proposed by Guo and Hall,15 with parameters from Figure 7 of Gennemark et al.,16 was used to compare the BW‐EI relationship to previous data. The data on AZD1979 relating EI reduction and RO in the mouse were generated from 3‐week BW studies in diet‐induced obese mice exposed to compound 88, compound 99, or AZD1979.

The MCHr1‐specific relationship between reduction of BW and EI in the rat was based on data from rats exposed to compound 99 or vehicle for 3 weeks. The data relating BW reduction and RO in the rat were collected from ALB‐exposed animals.11

The Supplementary Text gives further details of those studies.

Step 3. Exposure and receptor occupancy in the mouse

Exposure and ex vivo RO were measured, as described in Johansson et al.9 In Figure 4, the upper row reports data from a single‐dose acute experiment on lean C57BL/6 mice, whereas the bottom row reports data from an experiment in diet‐induced obese mice using the same setup as described in Johansson et al.9 but running only over 4 days.

Figure 4.

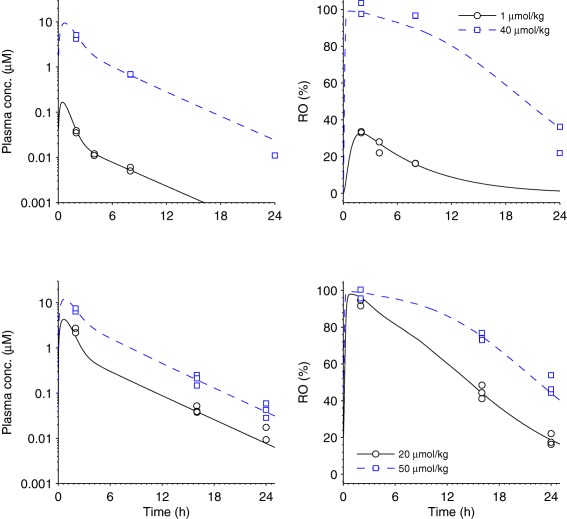
Receptor occupancy (RO) in humans to exposure in humans (step 3). Mouse exposure and RO data and model fit. Each row represents one experiment. The left column reports exposure data (squares and circles) and pharmacokinetic (PK) model fit (solid and dashed lines) for various doses indicated by the legends. The PK model was defined by the absorption rate k_a = 1.93 (1.6, 2.4) h⁻¹, the volume of distribution of the first compartment V₁ = 2.02 (1.6, 2.4) L × kg⁻¹, the maximum elimination rate V_max = 8.19 (7.6, 9.0) µmol × h⁻¹ × kg⁻¹, the Michaelis‐Menten constant K_m = 2.44 (2.3, 2.8) µmol, the intercompartmental clearance Q = 1.54 (1.3, 1.8) L × h⁻¹ × kg⁻¹, the volume of distribution of the second compartment V₂ = 5.01 (4.4, 5.7) L × kg⁻¹, and σ² = 0.104 (0.051, 0.15) µmol2 × L⁻², whereas the 5th and 95th percentiles are given within brackets. The right column gives RO data (squares and circles) and pharmacodynamic (PD) model fit (solid and dashed lines) for the corresponding doses. In the PD model, the total receptor concentration (R_tot) was fixed on a relative scale at 100%, the rate constant k_off = 0.210 (0.18, 0.25) h⁻¹, the dissociation constant K_D = 0.0837 (0.078, 0.091) µmol × L⁻¹, and σ² = 18.8 (8.9, 29) µmol2 × L⁻². The upper row represents a single‐dose acute experiment on lean mice, whereas the bottom row represents an experiment with chronic twice daily dosing on diet‐induced obese mice.

The system was modeled with a PK/PD‐link model, consisting of a two‐compartment PK model, with first order absorption and saturated elimination, and an RO PD model with elementary kinetics (Supplementary Text). Estimation was performed according to a maximum‐likelihood approach with a multiplicative log‐normal error model for exposure data and multiplicative normal error model for RO data, and using naïve‐pooled data for both cases. Uncertainty of parameter estimates was determined by bootstrapping, sampling single measurements randomly with replacement within each experiment (N = 300).

Software

Code for step 1 was written in Python version 2.7 software, using CasADi version 2.4.40 Other code was written in MATLAB (R2014a; The MathWorks, Natick, MA). The MATLAB function “grabit” was used for digitization in step 1 and 2, and “fminsearch” was used for the optimization problems of step 3. The code is provided in the Supplementary Code Files.

RESULTS

The objective of the MCHr1 antagonist drug‐discovery program was to devise a safe and efficient drug candidate with a competitive predicted clinical BW decrease of 10% over 1 year. Translation was divided into four parts, starting from the desired BW loss and going back to the predicted dose of AZD1979 (Figure 1).

Step 1. What reduction in energy intake leads to 10% body‐weight reduction over 1 year in humans?

We first wanted to predict the required EI decrease in humans resulting in a 1‐year BW loss of 10%. Data from several pharmacological studies indicate that BW first decreases and then plateaus after roughly 1 year (Figure 2). The corresponding inferred EI profiles typically display an initial drop followed by a return to levels close to the untreated levels (Figure 2).

The curves of Figure 2 reach an average BW loss of 9.4% after 1 year of treatment. Using slightly shifted curves, we next elucidated the typical forms of EI and BW time profiles resulting in exactly the targeted 10% BW decrease (Supplementary Figure S1). Over the 14 studies, the average EI reduction required over 1 year was 14% with an SE of 0.7%. Hence, regardless of EI and BW curvature, the required reduction was relatively stable.

The nonplacebo‐corrected BW curves analyzed hitherto approximately reach the desired level of 10% loss over 1 year, but may be confounded by drug‐independent weight changes. Placebo‐corrected curves measure drug‐dependent weight changes, but greater curve‐shifts are needed to obtain the desired levels of 10%. Hence, there is a balance between using only drug‐related weight‐change curves and the need for extrapolation. Repeating the analysis with placebo‐corrected data (reaching on average 6.2% BW loss over 1 year before the curve shift) gave, however, the same result – about 14% EI reduction over 1 year is required to decrease BW by 10% (Supplementary Figures S2 and S3, Supplementary Table S1, and Supplementary Text).

Step 1 was pivotal as a starting point for the human biomarker path, but also useful in isolation to inform the clinical design. Predictions of the required EI decrease and corresponding BW decrease for prespecified study durations were useful when defining stop‐go criteria for clinical studies (Table 1).

Table 1.

Predicted decrease of body weight and energy intake when targeting 10% body‐weight decrease in 1 year

Time	BW decrease, %	EI decrease, %
1 week	1.0	22
2 weeks	1.4	22
1 month	2.4	22
3 months	5.4	21
6 months	8.2	18
12 months	10	14

BW, body weight; EI, energy intake.

Predicted decrease in BW and EI (mean over the time period) when targeting 10% BW decrease in 1 year (reported values are the medians from the 14 considered clinical studies). For example, a 2‐week study with an EI decrease of 22% and BW reduction of 1.4% is expected to lead to 10% BW loss over 1 year.

Step 2. What receptor occupancy is required for a sufficient energy‐intake reduction?

There is no clinical data connecting MCHr1 occupancy to EI in humans. Therefore, we quantified this relationship in rodents and then translated it to humans.

The time period to study the average relative EI reduction of 1 year in humans was assumed to correspond to 3 weeks in rodents. This assumption is supported by the fact that a 3‐week time span in rodents compares reasonably well with a 1‐year life span in humans, adjusting for average life expectancy of the species.41 It is further supported by the similarity between drug‐induced rodent BW profiles over 3 weeks (Figure 3 C,D) and corresponding human profiles over 1 year (Figure 2 , Supplementary Figure S2), and between observed rodent EI profiles over 3 weeks (Figure 3 A,B) and the corresponding predicted human profiles over 1 year (Figure 2 , Supplementary Figure S2). Furthermore, at least for the rat, the relationship obtained between BW and EI reductions for drugs evaluated in step 1 agrees reasonably well with the inferred relationship for AZD1979 (Figure 3 F). For the mouse, corresponding data are too sparse to draw any conclusions (Figure 3 E).

The receptor occupancy to energy‐intake relationship in rodents

We established what RO is required to achieve on average 14% EI reduction (corresponding to 10% BW reduction in humans according to step 1) in rodents.

For the mouse, data on BW reduction vs. EI reduction indicated a linear relationship (Figure 3 E). Specifically, an average EI reduction of 14% over 3 weeks resulted in a BW reduction of about 12% (thick gray lines in Figure 3 E). Furthermore, based on the assumption that AZD1979 mainly targets EI and not EE, the mathematical model15, 16 also predicted a linear relationship (dashed line in Figure 3 E). The shift of the observed data compared to the model prediction (dashed line in Figure 3 E) indicates a minor drug effect on EE in line with previously reported data.10, 42, 43

Data on BW reduction vs. trough RO (24 h) from several compounds of the chemical series indicated a linear relationship (Figure 3 G; Supplementary Figure S4 for model choice). A BW reduction of about 12% required RO of 62% at 24 h in the mouse (thick gray lines in Figure 3 G). The sought relationship between EI reduction and RO at 24 h directly followed from the two above relationships: an average EI reduction of 14% over 3 weeks gave a BW reduction of about 12% and required RO of 62% at 24 h in the mouse.

For the rat, data on BW reduction vs. EI reduction indicated a linear relationship (Figure 3 F). Specifically, an average EI reduction of 14% over 3 weeks gave a BW reduction of about 4% (thick gray lines in Figure 3 F). It was not possible to judge a potential drug‐induced effect on EE from these data. Rat pair‐feeding data on MCHr1 antagonists are sparse in the literature; however, one 7‐day study suggests a minor effect on EE.44

Data from ALB on 4‐week BW reduction vs. RO at 24 h indicate a linear relationship as for the mouse (Figure 3 H). Specifically, a BW reduction of about 4% requires an RO of 37% at 24 h in the rat (thick gray lines in Figure 3 H). Similar to the mouse, the relationship between EI reduction and RO at 24 h was obtained from the two above relationships: an average EI reduction of 14% over 3 weeks gave a BW reduction of about 4% and required RO of 37% at 24 h in the rat.

Translating the receptor occupancy to energy‐intake relationship from rodent to human

The required RO level (point estimate 50%, range 37–62% for mouse and rat) at trough (24 h) was translated to the same level, 50%, but at 16 h in humans. The difference in coverage (24 h in rodents to 16 h in humans) was motivated by fundamentally different feeding behaviors in the two species. Humans typically have a prolonged period of fasting during the night45 when a drug effect would not be needed. Potential patients with significant nocturnal eating habits may be filtered out from clinical trials and future clinical use by using a questionnaire. In mouse, it is well established that ∼30% EI takes place during the (12 h) rest period.46 In the rat, the corresponding figure is 20–30%.47, 48

Step 3. What exposure is required to induce sufficient receptor occupancy?

We assumed that the RO parameters (K_D and k_off) scale from mouse to human (K_D is protein‐binding corrected). Fundamental for this assumption is central nervous system exposure in man. AZD1979 shows appropriate physicochemical properties for a central nervous system indication and excellent permeability without active efflux,9 hence supporting this assumption.

To estimate K_D and k_off we fitted a PK/PD‐link model to exposure and RO data from AZD1979‐treated mice (Figure 4). The model fits reasonably well to data and key parameters were determined with relatively high precision (Figure 4 ; residual plots in Supplementary Figure S5). Specifically, k_off was estimated to 0.210 (0.18, 0.25; 5th and 95th percentiles) h⁻¹, and K_D to 0.0837 (0.078, 0.091) µmol × L⁻¹.

Step 4. Prediction of the human pharmacokinetics

The human PKs were obtained by scaling using standard methods and data (Supplementary Table S2). The volume of distribution at steady‐state (V_ss) was predicted to 4.0 L/kg based on Oie‐Tozer's method using dog and rat PK data. The prediction of V_ss to man is likely to be good, because: (i) the compound shows a consistent free V_ss across species (i.e., the slope of a simple unbound allometric plot is 0.93 and, hence, between 0.8 and 1.2); and (ii) the apparent V_ss measured in preclinical species was broadly consistent with expectations for the chemical class and physicochemical properties of the compound (Rodger's and Rowland's tissue composition measure49, 50).

AZD1979 was found to be mainly eliminated by metabolism, and metabolic clearance (CL) was estimated to 8.6 mL/min/kg based on the mean of the in vitro‐in vivo extrapolation method (from repeated estimates of intrinsic CL in hepatocytes51) and the Liver Blood Flow method.52 There was good agreement between observed CL and predicted CL based on hepatic intrinsic CL, both in the rat and dog (roughly correct prediction in the rat and 1.3‐fold underprediction in the dog). Besides, other methods predicted similar CL, making our dose prediction robust. The bioavailability was predicted to 60% (first passage and liver blood flow = 20 mL/min/kg).

The predicted human PK was represented by a one‐compartment PK model with first order absorption and linear elimination.

Integrating steps 1–4 into a human dose‐prediction

Based on the target of 10% BW loss, and following the scaling path as depicted in Figure 1, the predicted human dose was 35 mg b.i.d. (Figure 5). The uncertainty in the human prediction was mainly influenced by the assumptions of each step in the scaling path. A sensitivity analysis illustrates that the human dose‐prediction was most sensitive to uncertainties in CL on the PK side, and to uncertainty in required RO and K_D on the PD side (Table 2). Naturally, the nonquantifiable translational assumptions cannot be captured in this analysis.

Figure 5.

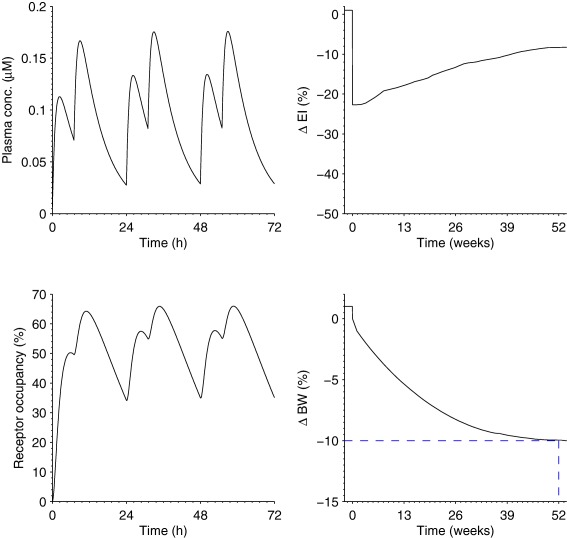
Human dose‐prediction of AZD1979. Predicted plasma‐concentration (upper left), receptor occupancy (RO; lower left) that is >50% during 16 h of the day, energy‐intake (EI) profile (upper right) with a 1‐year average of −14%, and body‐weight (BW; lower right) profile reaching a 10% decrease in 1 year. The EI profile is a nonparametric curve obtained from the average of the inferred curves of the 14 drugs of step 1.

Table 2.

Sensitivity of the predicted human dose to changes in key input parameters

	Factor change in CL/Vss/KD/koff
	0.5	0.67	1	1.5	2
Sensitivity of dose to CL	0.32	0.49	1	2.8	11
Sensitivity of dose to Vss	1.4	1.2	1	0.91	0.87
Sensitivity of dose to KD	0.5	0.67	1	1.5	2
Sensitivity of dose to koff	0.91	0.95	1	1.04	1.07
	Length of rodent EI‐BW studies, weeks
		2	3	4a
Sensitivity of dose to rodent EI‐BW study length		0.58	1	1.2
	Required change in EI, %
	10%	12%	14%	16%	18%
Sensitivity of dose to change in EI	0.62	0.81	1	1.2	1.5
	Required RO
	30%	40%	50%	60%	70%
Sensitivity of dose to RO	0.41	0.63	1	1.5	2.4
	Required RO coverage
	8 h	12 h	16 h	20 h	24 h
Sensitivity of dose to RO coverage	0.72	0.80	1	1.4	2.1

BW, body weight; CL, clearance; EI, energy intake; K_D, dissociation constant; k_off, dissociation rate; RO, receptor occupancy; V_ss, volume of distribution at steady‐state.

Sensitivity of the predicted human dose (expressed as a factor change; the point prediction is 1) to changes in key input parameters. The column of the point prediction is shaded in gray.

^aThe 4‐week data were extrapolated assuming that BW had reached steady‐state at 3 weeks, and that the EI of each day of the fourth week was the same as the EI of the last observed day (at 3 weeks).

DISCUSSION

The biomarker map formed the basis for the translational reasoning of AZD1979. The map generally facilitates communication of the mathematical model and interpretation of biomarker responses across species. It is moreover useful for the design of studies (e.g., concerning stop/go‐criteria), for forward (e.g., rat to human) and backward (e.g., rat to mouse) translation (c.f. Supplementary Figure S6), for identifying potential gaps in the data, and for investigating competitor compound characteristics or safety aspects in various species (e.g., predicting RO in dog safety studies10). Low confidence in one relationship can be compensated for by many alternative routes between biomarkers in different species. The prediction reliability critically depends on the most uncertain part of the biomarker path. The use of a mixture of modeling techniques is not atypical in translational modeling. Focus should be on finding the most appropriate model for each individual step based on the amount and quality of data and prior information.

Step 1 translated BW to EI based on semimechanistic body‐composition models and input estimation. A main alternative to the input‐estimation approach is to use a parametric analysis.53 The inferred average EI reduction of 14% over 1 year is in agreement with predictions by Rahmandad19 who expressed BW loss in terms of body mass index units (11–14% EI reduction required; assuming body mass index of 35 kg/m2, and interpolating between reported body mass index changes of 1 and 5 units). Furthermore, the relationship between BW loss after 4 weeks with BW loss after 23–26 weeks presented in the meta‐analysis of obesity studies by Plock et al.54 compares reasonably well with the inferred relationship in our analysis mainly concerning patients with diabetes, given that different patient populations were considered.

Both the analysis on the active arms and the analysis on placebo‐corrected data suggested the same required EI reduction of 14% for a 10% BW loss over 1 year, adding confidence to the derived estimate. Moreover, the dose prediction is not highly sensitive to required EI reductions in the interval 14 ± 2% (Table 2). The main uncertainty is likely that no clinical MCH‐antagonist data were available for the analysis. However, corresponding rat data do not suggest that MCH antagonists should deviate from other mechanisms with respect to the EI‐BW relationship (Figure 3 F).

It cannot be excluded that an initial large reduction in EI is required for an average EI decrease of 14%, and the desired BW loss. When comparing data from rodents and humans, we note that the BW decreases tend to plateau at the end of the respective studies, giving us confidence that steady‐states had been reached within the study periods of 3 weeks and 1 year. It seems that the initial EI decline is more pronounced in rodents compared with humans. The development of translational temporal models (c.f., Gennemark et al.41) would benefit from EI and BW data for individuals in time series for several compounds in both rodents and humans. This is an area of future research.

Step 2 empirically related RO and EI in rodents by linear regression of mostly 3‐week data. The relatively modest sensitivity of the predicted human dose to an increasing study length confirms that the chosen length was reasonable (Table 2). For the rat, we made one comparison of 3‐week and 4‐week BW decreases (Figure 3 F,H), which may be misleading. However, as less BW reduction typically occurs the last week compared to the earlier weeks (c.f., Figure 3 D), we judged this error as small compared with other sources of errors.

Initial AZD1979‐mediated BW loss in diet‐induced obese mice is driven by decreased EI, but an additional component of preserved EE is apparent in pair‐feeding and indirect calorimetry studies.10 Therefore, the model‐predicted relationship (the dotted line in Figure 3 E) may predict the EI‐driven effect on BW loss more reliably compared to the inferred relationship from observed data (the solid line in Figure 3 E). However, a similar rescaling of the BW axis would then be necessary to the BW‐RO relationship (Figure 3 G). These two operations would cancel each other out, and the sought after RO to EI relationship would not change.

The translation of RO to EI between rodents and humans is probably the most uncertain step in the human dose prediction. First, rodent obesity models may not translate perfectly to humans, as reported by Vickers et al.55 However, some of the observed variation may be due to the fact that Vickers' comparison is based on dose‐to‐effect and not on free concentration to effect. Second, translation of MCHr1 antagonists may be affected by the different number of receptor isoforms: two MCH receptor isoforms in humans compared to one in rodents. Mouse knock‐in experiments indicate that MCHr2 may counter drug‐induced appetite suppression by the MCHr1 path.56 On the other hand, AZD1979 reduced BW in dogs, which have two receptor isoforms like humans.10 Additionally, the sensitivities of the human dose to the required RO and to the RO coverage were relatively large (Table 2). Generally, step 2 could be improved by generating data from additional species, and by consistently using the same study length and only administer AZD1979.

Step 3 predicted the PK to RO relationship by PK/PD modeling. The human dose was largely insensitive to the prediction of k_off, but proportional to the K_D estimate (Table 2). For AZD1979, it was possible to observe RO in the mouse, but there was no target‐mechanism biomarker. The RO method led to efficient compound screening, as previously reported,9 and it was used in steps 2 and 3 in the dose prediction. In general, RO data may be lacking, and one must cope with significantly reduced biomarker information (e.g., only observations of dose and EI57). This increases the complexity and cost of compound screening, and animal proof‐of‐mechanism studies. For the AZD1979 prediction, one could alternatively have relied on exposure‐EI data for several species (e.g., mouse, rat, and non‐human primate). Taking many species into account may increase translational robustness, but sparse biomarker information may increase the risk of data misinterpretation.

Step 4 scaled the human PK by standard empirical methods based on cellular data and animal PK data. The dose prediction is relatively insensitive to the volume of distribution prediction, whereas there is greater sensitivity to the clearance prediction (Table 2). An alternative approach would be to use a physiologically based PK model.

Ideally, one would like to combine in vitro cellular data with a human systems‐pharmacology model, and avoid animal experiments. However, a full in vitro and in silico approach is difficult to achieve for new targets or compound classes, or both. For MCHr1 antagonists, the pharmacological system and full biomarker path are currently not sufficiently well characterized to allow such models. Besides, animal safety studies have to be interpreted in the right context. Therefore, focus has been to integrate animal and human data, both from AZD1979 and other MCHr1 antagonists, into a consistent framework to improve overall confidence in individual relationships by cross‐species validation.

CONCLUSIONS

In summary, the translational modeling used in the discovery of AZD1979 closes the scaling path from rodent to man, as well as from dose to effect level, and thereby allows forward simulation and input estimation across species. The work illustrates how modeling integrates data from several species and supports experimental design and human dose‐prediction. The approach might be of general interest for translation in the obesity field, and might inspire translational reasoning more broadly.

Supporting information

Supplementary Text. Further details on steps 1–3.

Supplementary Figure S1 Body weight to energy intake in human (step 1). Transformed summary curves of the 14 clinical studies reported in Figure 2.

Supplementary Figure S2 Body weight to energy intake in human for placebo‐corrected data (step 1).

Supplementary Figure S3 Body weight to energy intake in human for placebo‐corrected data (step 1). Transformed summary curves of the 14 clinical studies reported in Supplementary Figure S2.

Supplementary Figure S4 Model selection for body‐weight reduction to receptor occupancy in the mouse (step 2).

Supplementary Figure S5 Residual plots corresponding to the model fit in Figure 4.

Supplementary Figure S6 Fundamental operations on model representations of the biomarker chain.

Supporting Information Table 1

Supporting Information Table 2