Figure 2. A high critical phosphorylation for detachment creates a delay before detachment to solve the IPBO in a multisite phosphorylation model.
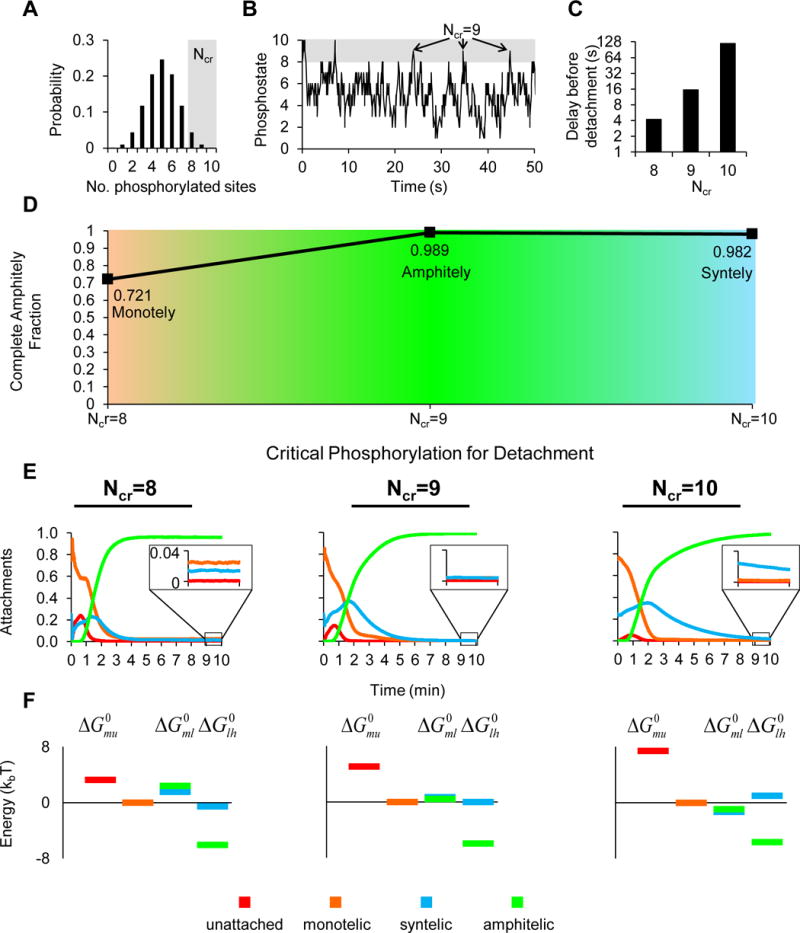
(A) When chromatin lacks tension, the number of sites phosphorylated follows a binomial distribution with N=10 sites and p=0.5 (probability of phosphorylation of each site). A high critical phosphorylation for detachment Ncr in the right tail of the distribution ensures a delay before detachment.
(B) A simulated kinetochore pair under low chromatin tension subject to kinase-mediated phosphorylation and phosphatase-mediated dephosphorylation demonstrates that the phosphostate of the kinetochore is on average 5 but reaches Ncr=8 infrequently, Ncr=9 very infrequently, and Ncr=10 extremely infrequently.
(C) As Ncr increases, the delay before detachment increases monotonically.
(D) Increasing the critical phosphorylation for detachment Ncr results in the emergence of an optimum in complete amphitely fraction (n=1000, 3600, 2800 simulated spindles for each Ncr =8,9,10; X2=1300, df=2, p<10−100; complete amphitely fractions for Ncr=8 and Ncr=9 were statistically significant, X2=20, df=1, p<10−5).
(E) The average attachments through time for the first ten minutes revealed how kinetochore attachments were obtained. Although the differences appear modest, amphitelic attachments rose more slowly and monotelic and syntelic attachments fell more slowly, as the delay before detachment increased. Insets between 9 and 10 minutes indicate that incorrect attachments were low for the intermediate delay before detachment but higher for the shortest and longest delays before detachment.
(F) The energy diagrams show that the energy change from low-tension amphitely to high-tension amphitely was most favorable in all cases. Although the differences were modest, as the delay before detachment increased, the energy change of monotelic to low-tension attachments decreased, facilitating passage to high-tension amphitely for the intermediate detachment time (when Ncr=9) and became negative for the longest detachment time (Ncr=10) which stabilized syntelic attachments and accounts for the small drop in complete amphitely over all spindles (Ncr=10, Figure 2D).
