Patient-Specific Simulations Reveal Significant Differences in Mechanical Stimuli in Venous and Arterial Coronary Grafts

Abstract

Mechanical stimuli are key to understanding disease progression and clinically observed differences in failure rates between arterial and venous grafts following coronary artery bypass graft surgery. We quantify biologically relevant mechanical stimuli, not available from standard imaging, in patient-specific simulations incorporating non-invasive clinical data. We couple CFD with closed-loop circulatory physiology models to quantify biologically relevant indices, including wall shear, oscillatory shear, and wall strain. We account for vessel-specific material properties in simulating vessel wall deformation. Wall shear was significantly lower (p = 0.014*) and atheroprone area significantly higher (p = 0.040*) in venous compared to arterial grafts. Wall strain in venous grafts was significantly lower (p = 0.003*) than in arterial grafts while no significant difference was observed in oscillatory shear index. Simulations demonstrate significant differences in mechanical stimuli acting on venous vs. arterial grafts, in line with clinically observed graft failure rates, offering a promising avenue for stratifying patients at risk for graft failure.

Introduction

Coronary artery bypass graft (CABG) surgery is performed in approximately 400,000 patients every year in the USA to revascularize ischemic myocardium [1]. Most patients undergoing CABG surgery require multivessel revascularization, and while arterial grafts offer superior patency rates, they are limited in availability. Hence, more than 70 % of CABG surgeries use autologous venous grafts. Despite advances in surgical techniques and post-surgical management, only 60 % of vein grafts remain patent and 50 % remain free of significant stenosis after 10 years, and event-free survival is as low as 40 % after 12 years [2] [3]. Late stenosis and vein graft occlusion, which account for the majority of adverse events, are primarily due to recurrent atherosclerosis [2]. Vein graft occlusion is associated with worse long-term outcomes [4, 5], and once grafts become completely occluded, they typically are not amenable to percutaneous intervention. In addition, repeat revascularization with percutaneous and surgical methods is associated with increased morbidity and mortality [6]. Thus, vein graft failure continues to pose a significant clinical challenge and economic healthcare burden.

Hemodynamics and wall biomechanics, influencing the behavior of the endothelial lining and regulation, as well as turnover and degradation of wall constituents such as fibroblasts and smooth muscle, play a key role as mechanobiological stimuli contributing to vein graft failure and disease progression [7, 8]. However, biologically relevant indices, including wall shear stress (WSS), oscillatory shear index (OSI), and wall strain, are not currently attainable via standard clinical measurement modalities. In addition, the prediction of post-surgical disease progression using vascular growth and remodeling (G&R) methods [9, 10] will require these mechanical stimuli as inputs. Without these data, it will likely be impossible to make patient-specific simulation-based predictions of risk of graft failure to risk stratify patients. Non-invasive quantification of mechanical stimuli is therefore a crucial first step towards improved understanding of the differential success rates of arterial vs. venous grafts. Image-based patient-specific computational fluid dynamic (CFD) simulations now offer a non-invasive means to quantify temporally and spatially resolved hemodynamics and wall mechanics quantities of clinical relevance.

We present a novel closed-loop multiscale CABG simulation framework that can predict local hemodynamics and wall mechanics using non-invasive clinical data. This framework includes fluid-structure interaction with appropriate arterial and graft material properties. The major objective of this work is to apply this framework to simulate graft hemodynamics and wall mechanics in patient-specific CABG geometries, and characterize differences in indices of mechanical stimuli between arterial and venous grafts. We hypothesized that patient-specific simulations would reveal significant differences in key mechanical stimuli that may predispose vein grafts to increased atherosclerosis progression. Specifically, motivated by clinical observations that venous grafts fail more often than arterial grafts, and that low shear and high oscillatory flow are correlated with atheroprone regions, we hypothesized that shear would be lower in venous grafts while atheroprone area would be larger than in arterial grafts. We also hypothesized that wall strain in venous and arterial grafts would be significantly different.

Methods

Patient Population

We identified five patients for this study who had previously undergone coronary artery bypass graft surgery and echocardiography, had no stents in the native coronaries or grafts, had undergone clinically indicated CT angiography, and were free of graft stenoses.

Clinical Data

CT angiography (CTA) was performed using a 64-slice Discovery CT750 HD scanner (GE Healthcare, Milwaukee, WI) according to clinical protocol. Subjects received beta blocking medication as needed to reduce heart rates to less than 65 beats per minute, and nitroglycerin (0.4 mg sublingual) was administered prior to scanning. All scans were performed using padded prospective gating centered at 75 % of the R-R interval with a slice thickness of 0.625 mm.

Echocardiograms were performed on four patients in accordance with standard guidelines [11]. Heart rates and blood pressures were measured at the time of echocardiography. Stroke volume was calculated from echocardiographic data as the product of the left ventricular outflow tract (LVOT) area and the velocity-time-integral of the Doppler measurement of flow through the LVOT [12]. Cardiac output was then calculated as the product of stroke volume and heart rate. For one patient (patient 3) with no available echocardiographic data, a body mass index-based population averaged cardiac output was used [13].

Simulation Methodology

The simulation methodology for each patient in the study, following prior patient-specific modeling approaches [14], consists of the following:

1. Construction of patient-specific models from CT images, including the aorta with branch vessels, coronary arteries, and grafts.

2. Formulation of mathematical models to mimic physiology, and tuning to determine model parameters that match clinical and literature data.

3. Solution of the governing equations of blood and vessel wall biomechanics and their interaction, to obtain primary time and spatially resolved flow and deformation fields in the 3D domain.

4. Post-processing to compute biologically relevant indices from the primary variables, including WSS, OSI, and wall strain.

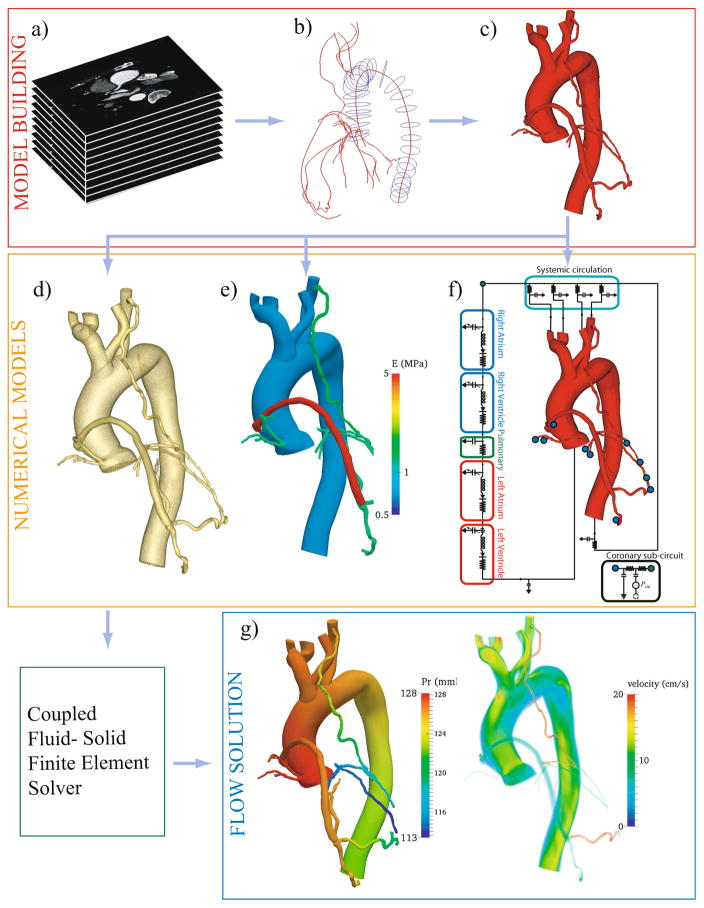
Each of these steps is illustrated in Fig. 1 and is explained in detail in the paragraphs below.

Fig. 1.

Simulation methodology for coronary artery bypass graft (CABG) patients in SimVascular (www.simvascular.org). Major steps in the pipeline are (a) acquire CT image of a CABG patient, (b) create centerline paths and segment the lumen, (c) loft the segmentations to form a 3D model, (d) discretize the 3D model into a finite element mesh, (e) assign material properties, (f) tune lumped parameter network to match clinical and literature targets, (g) solve governing equations on patient-specific models. Analyze and post-process results to determine clinically relevant quantities

Anatomic Model Construction

The 3D patient-specific anatomic CABG models were segmented from CT axial images (Fig. 1(a)) using the open source SimVascular software (www.simvascular.org). Models included the coronary arteries, aorta, aortic arch branch vessels, and bypass grafts. Paths were constructed along the vessel centerlines to the limits of CT resolution. Vessel lumens were then segmented on 2D slices perpendicular to the paths (Fig. 1(b)). The segmentations were lofted together to produce a patient-specific 3D model (Fig. 1(c)).

Numerical Models: Preprocessing

3D patient-specific models require a series of preprocessing steps to render them suitable for simulation. Steps involved in preprocessing are (a) discretization (meshing) of the 3D model, (b) assignment of material properties to vessel walls, and (c) determination of boundary conditions to mimic the circulatory and coronary physiology.

All models are discretized into linear tetrahedral finite elements to make them suitable for finite element simulation using the commercial package MeshSim (Simmetrix Inc., Clifton Park, NY). Mesh independence is guaranteed by successive mesh adaptation [15], resulting in meshes of approximately 4 million elements for each model (Fig. 1(d)).

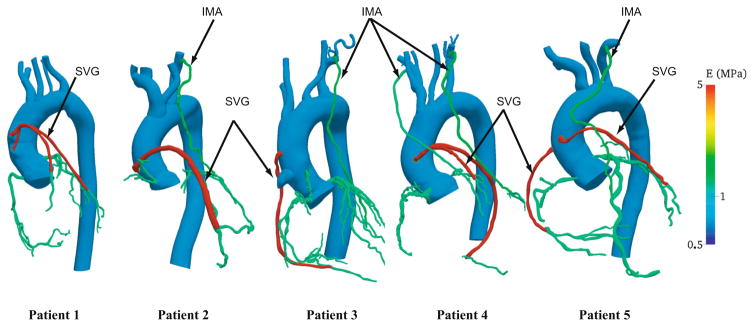
Fluid-structure interaction studies require vessel wall thickness and material properties as inputs, which are usually unattainable by non-invasive CT imaging. While some recent studies have obtained thickness values from intravascular ultrasound (IVUS) or optical coherence tomography (OCT), we chose to restrict this study to data commonly available from standard of care non-invasive clinical measurements. Hence material properties are assigned based on literature values (Fig. 2) [16–18]. Thickness values of the coronary arteries are assigned based on morphometric measurements from the literature [19]. For the aorta, arch branches, and grafts, motivated by a constant homeostatic circumferential stress hypothesis, thickness is calculated from radius-thickness ratios in the literature [16, 20]. The thickness and material properties are then propagated over the patient-specific geometry by solving a homogenous Laplace partial differential equation, with prescribed values at the inlets and outlets [21]. This method accounts for local curvature, vessel branching, and change in vessel properties across branches and anastomoses. This results in a smooth distribution, which is computationally convenient and requires minimal user input (Fig. 1(e)).

Fig. 2.

Young’s modulus (MPa) distribution in a cohort of patient-specific coronary artery bypass graft (CABG) models. The following material property values were assigned based on literature data: Aorta and the arch walls—0.7 MPa, left and right coronaries—1.15 MPa, left internal mammary artery—1.4 MPa, right internal mammary artery—1.15 MPa, vein grafts—5 MPa

To model the circulation outside of the 3D domain, including the heart, systemic circulation, and microcirculation, we make use of a circuit analogy, in which pressure drop is analogous to voltage and flow is analogous to current, thereby relating compliance to capacitance, viscous dissipation to resistance, diodes to valves, etc. We use a closed-loop lumped parameter network (LPN), with circuit blocks representing the four chambers of the heart, systemic and coronary circulations (Fig. 1(f)). The LPN is coupled to the 3D model using an implicit, modular coupling algorithm with excellent stability properties [22]. While a standard RCR circuit (Windkessel) is sufficient to model the systemic circulation, the coupling between the myocardium and the coronary arteries poses additional challenges and standard boundary conditions are not sufficient. Ventricular contraction exerts extravascular forces on the coronary arteries, causing increased resistance during ventricular contraction and causing the coronary flow to be out of phase with the systemic circulation. Hence, coronary specific boundary conditions [23, 24] coupled to the intramyocardial pressure are used at all coronary artery outlets in the model. We use an elastance function to model the ventricular pressure-volume relationship [23, 24] with an activation function to model the atria [25]. The LPN parameters are tuned to match standard-of-care non-invasive clinical measurements. The following data were used for tuning: cardiac output (CO), heart rate (HR), systolic and diastolic blood pressure, and literature data to provide additional targets, as summarized in Table 2. We assumed 4 % of the total cardiac output was distributed to the coronary arteries [26]. Motivated by Murray’s law, a mathematical relationship between vessel size and flow, an area-based approach was used to assign capacitance and resistance values at the outlets. Capacitance values were chosen to be proportional to outlet area, and resistances values were determined according to a modified Murray’s law using an exponent of 2.0 for the aortic branches and 2.6 for the coronary branches [27, 28]. The equations governing the LPN, and methods for their solution, follow our previous work [24].

Table 2.

Summary of tuned targets

Patient ID	BP-clinic (mmHg)	BP-sim (mmHg)	SV-clinic (ml/cycle)	SV-sim (ml/cycle)	%CO to Cor-lit	%CO to Cor-sim	L-R flow-sim in %
Patient 1	124/73	118/74.5	60.9	63.5	4.0	4.0	65.7–34.3
Patient 2	133/85	133/85.5	80.4	84.7	4.0	3.9	82.0–18.0
Patient 3	135/78	133/78	78.1a	75.8	4.0	4.0	52.5–47.5
Patient 4	115/74	117/74	115.1	114.8	4.0	4.1	56.4–43.6
Patient 5	113/69	115/68	70.5	70.6	4.0	4.1	74.0–26.0

Summary of non-invasive clinical measurements, population averaged targets from literature and respective quantities from simulations. The LPN was tuned to match, within 10 % error, a combination of non-invasive clinical measurements for the patient and population averaged values from literature

BP blood pressure (mmHg), SV stroke volume (ml/cardiac cycle), % CO to Cor percentage of cardiac output perfusing the coronaries, L-R left-right coronary flow expressed in percentage, -clinic value from clinic, -sim value from simulation, -lit value from literature

^aNo echocardiogram data for patient, body mass index-based population average was used

Computational Simulations

Quantification of pressure, velocity, and displacement fields require numerical solution of a coupled system of equations to model wall deformation and blood flow. We use SimVascular to solve the time-dependent incompressible Navier-Stokes equations for the fluid domain and Cauchy’s equations of linear elasticity for the vessel wall using a stabilized finite element method [29]. An efficient resistance-based preconditioner is used to solve the linear system in the SimVascular flow solver [30].

For fluid-structure interaction, we employ the coupled momentum method (CMM) [29], which has been verified and validated previously against analytic and in vitro experimental data with excellent agreement [31], and is computationally less expensive than standard arbitrary Eulerian Lagrangian (ALE) approaches because it relies on a fixed-mesh, small deformation assumption. The fluid and solid systems couple and interact at the surface of the vessel, where the wall imposes tractions on the fluid domain, translating to deformations and velocities on the fluid mesh and fluid imparts forces on the wall, resulting in displacements.

Blood is modeled as an incompressible Newtonian fluid, with density 1.06 g/cm³ and viscosity 0.04 dyn/cm²-s. Walls are modeled as a linear elastic material with Poisson ratio of 0.5.

The simulations were run on XSEDE NICS resource-Darter which is a Cray XC30 system with the compute nodes made of two 2.6 GHz 64 bit Intel 8-Core XEON processors. One cardiac cycle on a mesh of approximately 4 million elements required about 10 h on 96 processors. The entire simulation process, from image data to model construction and deformable simulation on a 4-million-element model, took approximately 3 weeks for each subject.

Calculation of Mechanical Stimuli and Geometry

We post-processed simulation results to compute indices of presumed biological relevance, specifically time averaged wall shear stress (TAWSS), OSI, percentage of graft surface area where WSS was less than a pathological value (which we refer to as atheroprone area, A_athero), and wall strain quantified through a scalar measure—Green Strain Invariant (GSI1) (see Appendix for mathematical details). These quantities were spatially and temporally averaged over each graft over one cardiac cycle. For statistical analysis, TAWSS in each graft was normalized by the aortic value of TAWSS in the same patient to normalize for patient variability. Every simulation was run for at least six cardiac cycles and these quantities were computed for the final cycle after initial transients had died out. In addition to mechanical stimuli, we also quantified graft diameter and tortuosity and quantified the differences between the two graft types. Methods for diameter and tortuosity calculations are described in the appendix.

Statistical Analysis

The graft population was small and statistical distributions were not known a priori; hence, we used a Wilcoxon Rank Sum test from the SciPy library (v0.13.3) in Python [32] to determine statistical significance among the parameters investigated, with p values <0.05 considered to be statistically significant. Mean values of the following indices were compared for venous vs. arterial grafts: (1) WSS, (2) OSI, (3) A_athero, and (4) wall strain. Since WSS and OSI are directional in nature, p values for quantities 1–3 above are reported for one-tailed tests only. For wall strain, two-tailed tests were used. Mean values of diameter and tortuosity were also compared for venous vs. arterial grafts.

Results

Demographics of patients selected for this study, along with number of grafts and target vessels, are summarized in Table 1. We report results for 13 grafts (n = 5 arterial, n = 8 venous) from five subjects.

Table 1.

Patient demographic data and patent grafts

Patient ID	Gender	Age	Interval between CABG and CTA (years)	Patent grafts
Patient 1	F	48	13	SVG to LAD, SVG to OM
Patient 2	F	69	11	LIMA to OM1, SVG to LAD
Patient 3	M	72	17	LIMA to OM, SVG to distal RCA
Patient 4	M	61	1	RIMA to LAD, LIMA to OM, SVG Y graft—high DIAG and PDA
Patient 5	F	43	4	LIMA to LAD, SVG to OM, SVG to RCA

Summary of patient demographics and the grafts in each. The total number of grafts in the population was 13 (8 venous and 5 arterial)

SVG saphenous vein graft, LIMA left internal mammary artery, RIMA right internal mammary artery, OM obtuse marginal, RCA right coronary artery, LAD left anterior descending

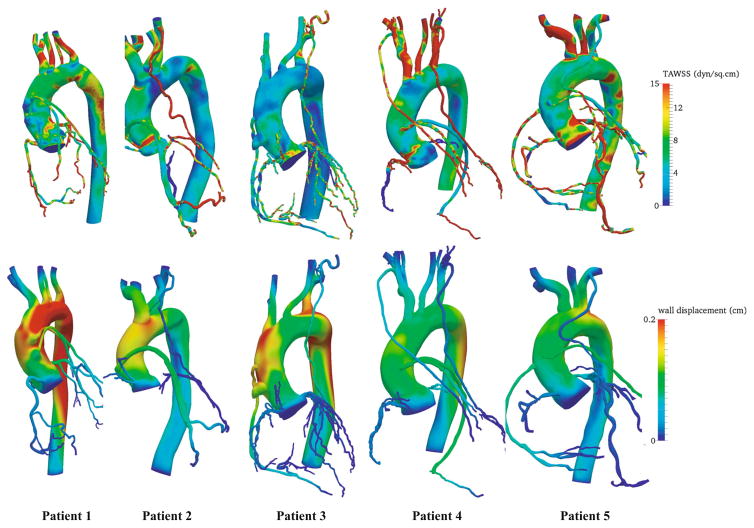
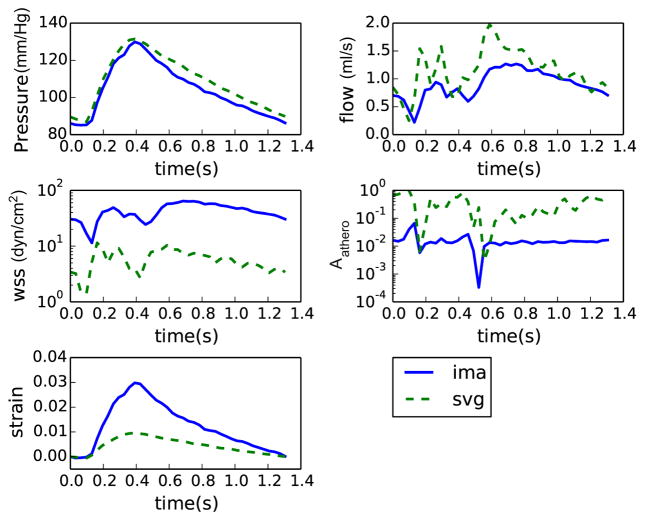
The LPN was tuned to match clinical and literature targets within 10 % error (Table 2). Contours of wall shear stress and wall displacements from the simulations are shown in Fig. 3 for all patients. The model captured the expected out of phase behavior of coronary and systemic flow and pressure waveforms. Representative comparisons of time-dependent quantities in venous and arterial grafts are shown in Fig. 4 for patient 2. Flow in the grafts was dominant during diastole, while pressure and strain were in phase with the systemic circulation (Fig. 4) as expected. In line with previous invasive measurements [26], the tuned LPN produced a high variability in the left-right flow split in coronaries (Table 2).

Fig. 3.

Representative solution fields in the patient-specific cohort. Top—time averaged wall shear stress (dyn/cm²), bottom—displacement (cm) field near peak systole

Fig. 4.

Representative pressure, flow, wall shear stress, A_athero, and strain values during a cardiac cycle in a venous and an arterial graft from patient 2. Note the flow and wall shear is dominant during diastole in these grafts, primarily because majority of flow in coronary occurs during diastole. Also note the WSS is higher and A_athero is lower in the arterial graft

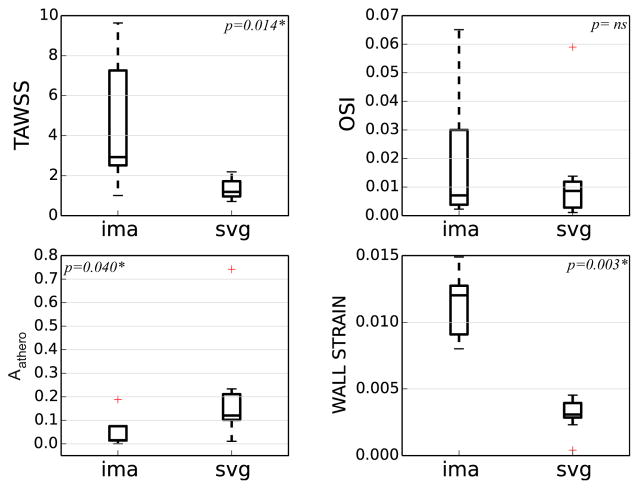
TAWSS was significantly lower (7.5 ± 3.2 dyn/cm² in venous grafts vs. 23.2 ± 15.9 dyn/cm² in arterial grafts, p = 0.014), and A_athero was significantly higher (0.20 ± 0.21 in venous grafts vs. 0.06 ± 0.07 in arterial grafts, p = 0.040) in venous grafts compared to arterial (Fig. 5). Wall strain was significantly higher in arterial grafts (0.003 ± 0.001 in venous grafts vs. 0.011 ± 0.002 in arterial grafts, p = 0.003). No significant difference in OSI was found between arterial and venous grafts (0.022 ± 0.024 in venous grafts vs. 0.013 ± 0.018 in arterial grafts, p = NS). Conclusions on significance remained unchanged when statistics were recomputed with log transforms and without aortic WSS normalization.

Fig. 5.

Box plot summary of normalized time averaged wall shear stress (TAWSS), oscillatory shear index (OSI), atheroprone area (A_athero), and wall strain in the arterial and venous grafts. Differences in TAWSS, A_athero, and wall strain between graft types were significant while differences in OSI were not (p < 0.05 is significant). Reported statistics are for five patients with a total of 13, arterial (n = 5) and venous (n = 8), grafts

Uncertainty associated with the value of threshold TAWSS motivated us to quantify the distribution of A_athero for different values of TAWSS threshold (Fig. 6). Regardless of the threshold value for critical wall shear stress, venous grafts consistently had a higher region of atheroprone area than arterial grafts, with the difference increasing and converging towards a constant value at higher threshold values.

Fig. 6.

Frequency distribution of A_athero by different WSS thresholds, averaged across all venous and arterial grafts in the cohort. The averaged A_athero regions in arterial grafts are consistently lower than the venous values, regardless of the WSS cutoff value

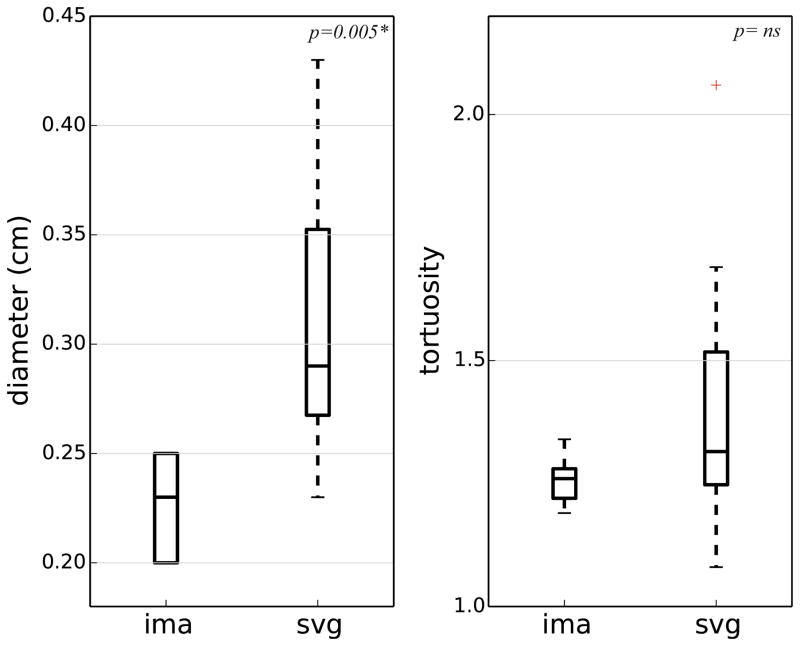
Mean venous graft diameter was significantly larger than arterial graft diameter (0.31 ± 0.06 in venous grafts vs. 0.23 ± 0.02 in arterial grafts, p = 0.005) and there was no significant difference in tortuosity (1.43 ± 0.29 in venous grafts vs. 1.26 ± 0.05 in arterial grafts, p = ns) (Fig. 7).

Fig. 7.

Summary of diameter and tortuosity of grafts in the cohort. The venous graft diameters were significantly larger than the arterial graft diameters (p = 0.005^*). The differences in tortuosity were not significant (p = ns). SVG—saphenous vein graft, IMA—internal mammary artery

Discussion

This study produced several major findings. First, the proposed framework successfully integrates patient-specific image-based models with fluid-structure interaction and closed-loop boundary conditions tuned to match non-invasively measured patient-specific clinical targets. Second, simulations predict significant differences in time averaged wall shear stress, area prone to atherosclerosis, wall strain, and graft diameter between arterial and venous grafts. Third, there were no significant differences in oscillatory shear index or graft tortuosity between arterial and venous grafts. Finally, we have quantified clinically and biologically relevant mechanical stimuli in coronary grafts that could guide the design of experiments in vascular biology.

Augmenting Clinical Practice with Non-invasive Modeling Tools

CABG remains an effective and widely used treatment for patients with multivessel coronary disease [33, 34]. While it is well-established that arterial grafts offer superior clinical performance, the necessity for vein grafts in the majority of CABG surgeries persists, and the mechanisms of vein graft failure remain poorly understood. There is a pressing need for earlier identification of patients at risk for graft failure. While CT imaging provides detailed coronary anatomy, it does not directly provide hemodynamics or biomechanics data. It is therefore likely that imaging alone is insufficient for early diagnosis of impending graft failure and patient risk stratification. Quantifying the mechanical stimuli acting on grafts in patient-specific models is a necessary precursor to understanding and predicting the complex mechanobiological process of graft failure.

The links between graft failure and mechanics have been challenging to isolate from myriad influencing factors including patient variability, clinical risk factors, differing clinical and surgical strategies, graft wall compositions, and adaptation in health and disease. The primary goal of this study was to quantify differences in mechanical stimuli between venous and arterial grafts with high fidelity patient-specific models of hemodynamics and physiology that account for patient variability and differing graft structural properties. These quantities are necessary inputs for future risk stratification metrics, vascular biology experiments, and growth and remodeling predictions.

Quantification and Role of Mechanical Stimuli

Recent advances in multiscale modeling [22–24, 29, 35] now permit physiologically realistic simulations in patient-specific coronary geometries, overcoming prior limitations of idealized geometries, rigid walls, and non-physiologic boundary conditions. The closed-loop boundary condition formulation we employ enables dynamic prediction of inlet and outlet pressure and flow waveforms, avoiding the need to directly prescribe these as in open-loop simulations. This is important since these data are typically not available from standard-of-care CT measurements. Rigid wall simulations must assume infinite wave propagation speed, which significantly alters low and pressure waveforms, and over-predicts pressure amplitudes. Hence deformable wall simulations are essential to accurately predict physiologic pressure levels. Also, material properties and wall thickness vary across the vasculature to withstand local loads [16, 17]. Integration of closed-loop boundary conditions, appropriate assignment of wall properties, and fluid-structure interaction are necessary for accurate prediction of mechanical stimuli in CABG simulations.

Wall Shear Stress

Wall shear stress in grafts was previously investigated invasively using Doppler flow wire velocimetry, area measurements from angiography, and wall shear computed with a Poiseuille flow assumption [36]. Results confirmed elevated shear stress of 16 ± 4 dyn/cm² for an IMA compared to 4.8 ± 1.6 dyn/cm² for an SVG, in patients with low-grade stenosis (50–75 %) in the native coronary arteries. The respective values for high-grade stenosis (>75 %) were 13.7 ± 4.9 dyn/cm² for an IMA and 4.6 ± 2.0 dyn/cm² [36]. Mean values of shear stress from our simulations not only mimic the observed qualitative trend of lower shear stress in SVGs compared to IMAs, but are comparable quantitatively. Low wall shear is also known to correlate with atheroprone regions in blood vessels [8]. Our findings agree with these observations, revealing that venous grafts have larger regions (with higher A_athero) where the graft is exposed to pathologically low WSS (<4 dyn/cm²) compared to arterial grafts. This conclusion did not change with different cutoff values for low WSS. Notwithstanding the absence of heart wall motion in our simulations, our findings are consistent with previous invasive measurements, clinical observations, and long-term outcomes on venous grafts. The large difference in WSS between arterial and venous grafts suggests that WSS may be a primary indicator of differential risk for vein graft failure that should be correlated with long-term clinical outcomes in future studies. While there are significant differences in both TAWSS and graft diameter, the increase in diameter alone is not sufficient to predict the difference in TAWSS between arterial and venous grafts. A larger study with outcome data will be necessary to determine any correlation between graft diameter, flow, material property, and measured outcomes.

Oscillatory Shear Index

Oscillatory shear index is a measure of oscillatory component in the flow. Regions of disturbed and recirculating flow, which have high oscillatory flow components, are known to disturb the endothelial lining, upregulate inflammatory pathways, and cause intimal hyperplasia in the vessel wall, which in turn creates conditions conducive to long-term atherosclerosis [37]. The venous and arterial grafts in our study did not exhibit significantly different OSI values. This is unsurprising when considering the similarity in curvature in both graft types, and the similarity in imposed pressure differences (systemic minus coronary) driving flow through the graft, which is the primary determinant of oscillatory flow.

Wall Strain

It is known that circumferential stress plays a primary role and WSS plays a secondary role in graft remodeling [38]. Mechanical stress/strain are known to alter the structure and function of wall constituents such as smooth muscle and reprogram gene expression, differentiation, migration, proliferation, and apoptosis [39]. Due to its influence on multiple functions, the role of strain and its underlying molecular mechanisms have been hard to elucidate in normal and pathological conditions. Nonetheless, our finding that strain is significantly lower in venous grafts compared to arterial grafts (Fig. 5) emphasizes the need to probe the role of circumferential strain in future studies on the long-term adaptation of grafts. We note that it is the structural stiffness (combined effect of Young’s modulus and thickness), and not material stiffness (Young’s modulus) alone, that determines the final strain state and hemodynamics in a vessel.

Furthering Models to Incorporate Biological Response

Venous coronary bypass grafts experience pressures of approximately 20 times and flows of 4 times their native environment, often leading to maladaptive response. While CFD tools enable quantification of the mechanical environment, one needs models of growth and remodeling to understand the underlying pathophysiology of maladaptation and correlate directly with clinical outcomes data on graft failure rates. Current efforts are directed towards incorporating cellular level details into mechanics-based models to capture growth and remodeling behavior of grafts in the presence of altered hemodynamics [10, 40]. Translation of these models requires patient-specific inputs from CFD simulations. Towards this end, we envision an integrated fluid-structure-growth model spanning scales from the cellular to vessel level, which would enable prediction of graft mechanics together with long-term adaptive response in individual patients. These combined models could also inform future vascular biology experiments, guide clinical data collection and outcomes correlations, and ultimately aid clinical decision-making.

Limitations

We recognize several limitations to our study. First, coronary wall motion is a superposition of radial motion due to pressure changes and translational motion imposed by the moving heart wall [41]. Effects of translational motion were not considered and would require more computationally expensive methods, as well as time-resolved CT data with increased radiation doses. Because the majority of coronary flow occurs during diastole, when wall motion is minimal, we felt justified in this assumption. Second, although the pathophysiological mechanisms of graft failure are not fully understood, it is known that the interplay between local hemodynamics and vascular biology determines long-term outcome of the graft. Our models lack the cellular and subcellular details required to capture the evolving nature of graft adaptation and subsequent disease progression. Current efforts are directed towards development of mechanics-based models of vascular growth and remodeling [40]. Recent efforts have also been directed towards systematic parameter estimation and uncertainty quantification, which could streamline the tuning process in CABG simulations [42]. Third, while the boundary conditions were tuned to patient-specific data, material properties and blood viscosity were not patient specific. These limitations could potentially be overcome in future work through the incorporation of IVUS or OCT data and patient-specific hematocrit measurements. Finally, the number of subjects and grafts studied in this pilot study was relatively small. This was in large part due to the significant time currently required for model construction and simulation. Current efforts are geared towards accelerating the model building and simulation processes through integration of machine learning and automation algorithms [43].

Translational Outlook

Computational simulations of coronary flow have gained recent attention with the FDA approval of HeartFlow’s FFR_CT (fractional flow reserve derived from CT) technology, with recent clinical trials demonstrating that simulations can reliably provide data previously only available via invasive catheterization procedures [44]. In addition, simulations have led to clinical translation of novel surgical methods in congenital heart disease with promising results [45, 46]. Development of simulation tools to predict venous graft failure poses additional challenges of incorporating long-term mechanobiological responses, and correlation with intermediate-long-term clinical outcomes.

Validation against clinical data is one of the major challenges in translation. Our solvers and boundary conditions have been validated against in vitro experiments, and against in vivo data in other clinical scenarios, but direct comparisons to patient-specific in vivo data in coronary arteries are still underway. These validations require in vivo measurements of flow, pressure, and wall displacements. However, these efforts are limited by challenges of small size, cardiac motion, and risks associated with invasive measurements in the coronary arteries.

The mechanical stimuli quantified in our study are motivated by biological experiments and are surrogates of cellular mechanobiologic response. Demonstration of the clinical utility of these indices will require larger patient cohorts and longitudinal data.

Conclusion

We presented a quantitative comparison of multiple hemodynamic and biomechanical indices in venous and arterial coronary bypass grafts. We found significant differences in mechanical stimuli with decreased wall stress and circumferential strain and increased atheroprone area in venous grafts. This work constitutes an essential step towards correlating these quantities with subsequent disease progression and clinical outcomes. Such correlations could enable early identification of patients at risk for graft failure, leading to improved medical management and closer follow-up in high-risk patient groups. In addition, simulations may yield insights to help optimize surgical techniques and hence decrease graft failure rates.

Abbreviation

CABG

Coronary artery bypass graft

CAD

Coronary artery disease

CFD

Computational fluid dynamics

CT

Computed tomography

GSI1

Green Strain Invariant1

IMA

Internal mammary artery

LPN

Lumped parameter network

OSI

Oscillatory shear index

SVG

Saphenous vein graft

WSS

Wall shear stress

Appendix

The following paragraphs elaborate the computation of mechanical stimuli indices from primary mechanics quantities such as velocity and displacements.

Time averaged wall shear stress (TAWSS) is computed as,

$$\text{TASWSS}=\frac{\text{mag}\left({\int }_0^{T_{\text{CC}}}\left(\overrightarrow{\text{WSS}}\right)dt\right)}{T_{\text{CC}}}$$

where $\left(\overrightarrow{\text{WSS}}\right)$ is the wall shear stress vector, the tangential traction force produced by blood moving across the endothelial surface, T_CC is the duration of one cardiac cycle, and mag indicates magnitude. For statistical analysis, TAWSS in each graft was normalized by the aortic value of TAWSS in the same patient to normalize for patient variability.

Oscillatory shear index, a measure of oscillatory component of the flow, is computed as,

$$\text{OSI}=\frac{1}{2}\left(1-\frac{\left|{\int }_0^{T_{\text{CC}}}\left(\overrightarrow{\text{WSS}}\right)dt\right|}{{\int }_0^{T_{\text{CC}}}\left|\left(\overrightarrow{\text{WSS}}\right)\right|dt}\right).$$

Atheroprone area (A_athero), a measure of the area of the graft prone to atherosclerosis, is computed as,

$$A_{\text{athero}}=\left(\frac{{\int }_{A_{\text{graft}}}\mathit{fdA}}{{\int }_{A_{\text{graft}}}\mathit{fdA}}\right),f=\{\begin{array}{l}1,\left|\overrightarrow{\text{WSS}}\right|<4\frac{\text{dyn}}{{\text{cm}}^2}\hfill \\ 0,\text{otherwise}\hfill \end{array},$$

with the threshold for low WSS set to 4 dyn/cm² based on literature data [47].

Amongst several potential measures of vessel wall strain, we chose to quantify Green Strain Invariant 1 (GSI1), a scalar measure of strain that is insensitive to rigid body motions, measured with respect to diastolic configuration [48]. This is calculated as

$$\text{GSI}1=tr\left(\frac{1}{2}\left(\overline{\overline{F}}{\overline{\overline{F}}}^T-\overline{\overline{I}}\right)\right),$$

Where $\overline{\overline{F}}$ is a tensor defined as the gradient of displacement vector, $\overline{\overline{I}}$ is an identity tensor and tr is the matrix trace operator.

Diameter was computed from lumen area by approximating the lumen area to be a circle. Lumen area was measured perpendicular to the vessel centerline and averaged across the length of the vessel. Tortuosity was defined as distance between points along the length of centerline divided by the distance between first and last point on the centerline and is a measure of deviation of centerline from a straight line.