Measurement of the distribution of ventilation-perfusion ratios in the human lung with proton MRI: comparison with the multiple inert-gas elimination technique

We report a comparison of a new proton MRI technique to measure regional V̇_A/Q̇ ratio against the multiple inert gas elimination technique (MIGET). The study reports good relationships between measures of heterogeneity derived from MIGET and those derived from MRI. Although currently limited to a single slice acquisition, these data suggest that single sagittal slice measures of V̇_A/Q̇ ratio provide an adequate means to assess heterogeneity in the normal lung.

Abstract

We have developed a novel functional proton magnetic resonance imaging (MRI) technique to measure regional ventilation-perfusion (V̇_A/Q̇) ratio in the lung. We conducted a comparison study of this technique in healthy subjects (n = 7, age = 42 ± 16 yr, Forced expiratory volume in 1 s = 94% predicted), by comparing data measured using MRI to that obtained from the multiple inert gas elimination technique (MIGET). Regional ventilation measured in a sagittal lung slice using Specific Ventilation Imaging was combined with proton density measured using a fast gradient-echo sequence to calculate regional alveolar ventilation, registered with perfusion images acquired using arterial spin labeling, and divided on a voxel-by-voxel basis to obtain regional V̇_A/Q̇ ratio. LogSDV̇ and LogSDQ̇, measures of heterogeneity derived from the standard deviation (log scale) of the ventilation and perfusion vs. V̇_A/Q̇ ratio histograms respectively, were calculated. On a separate day, subjects underwent study with MIGET and LogSDV̇ and LogSDQ̇ were calculated from MIGET data using the 50-compartment model. MIGET LogSDV̇ and LogSDQ̇ were normal in all subjects. LogSDQ̇ was highly correlated between MRI and MIGET (R = 0.89, P = 0.007); the intercept was not significantly different from zero (−0.062, P = 0.65) and the slope did not significantly differ from identity (1.29, P = 0.34). MIGET and MRI measures of LogSDV̇ were well correlated (R = 0.83, P = 0.02); the intercept differed from zero (0.20, P = 0.04) and the slope deviated from the line of identity (0.52, P = 0.01). We conclude that in normal subjects, there is a reasonable agreement between MIGET measures of heterogeneity and those from proton MRI measured in a single slice of lung.

NEW & NOTEWORTHY We report a comparison of a new proton MRI technique to measure regional V̇_A/Q̇ ratio against the multiple inert gas elimination technique (MIGET). The study reports good relationships between measures of heterogeneity derived from MIGET and those derived from MRI. Although currently limited to a single slice acquisition, these data suggest that single sagittal slice measures of V̇_A/Q̇ ratio provide an adequate means to assess heterogeneity in the normal lung.

ventilation-perfusion (V̇_A/Q̇) matching is the most important mechanism determining gas exchange efficiency (40) both in health and in disease. The ability to characterize V̇_A/Q̇ distributions allows important insights into lung physiology and pathophysiology (18, 35). We previously reported a new technique for measuring regional V̇_A/Q̇ matching using proton magnetic resonance imaging (MRI) (17). This technique combines arterial spin labeling (ASL) measures of regional pulmonary blood flow (5) with oxygen enhanced measures of regional specific ventilation (32) and fast gradient echo measures of regional proton density (20, 34) to quantify the regional distribution of V̇_A/Q̇ ratios. The technique has several advantages: it provides spatial data on the distribution of V̇_A/Q̇ ratios, is noninvasive, does not require ionizing radiation, and can be potentially implemented on any 1.5 T MR scanner without hardware modification.

As currently implemented, our technique for measuring V̇_A/Q̇ matching with proton MRI acquires data in a single 15 mm sagittal slice of lung, representing ~8% of lung volume. This is because the measures of regional specific ventilation use voxel-by-voxel measures of the regional MR signal intensity resulting from a change in inspired O₂ concentration in order to construct maps of regional specific ventilation, requiring 220 image acquisitions (32). Twenty images are acquired with the subject inspiring air and 20 images while inspiring 100% O₂. This cycle is repeated 5 times and an additional 20 breaths of 100% oxygen are added at the end of the cycle, taking ~18 min. In patients where a heterogeneous pattern of disease is expected, data from a single lung slice are likely not adequate to evaluate the pattern of V̇_A/Q̇ distributions. Although, modifications to the technique designed to address the single slice limitation are in development, given the advantages of the technique, we wished to determine if data from a single representative slice could accurately characterize the V̇_A/Q̇ distribution in normal subjects where the lung is expected to be more uniform, thus facilitating studies of normal pulmonary physiology.

The multiple inert gas elimination technique, MIGET, is a fully quantitative technique to directly measure V̇_A/Q̇ matching in humans (18, 19, 30, 38) and is widely used to characterize V̇_A/Q̇ mismatch (30, 35, 36). MIGET uses relationships between arterial, expired and mixed venous concentrations of trace amounts of marker gases dissolved in saline and infused intravenously, to solve for the distribution of V̇_A/Q̇ ratio in multiple gas exchange units. MIGET allows the distribution of ventilation, and perfusion to be expressed as a function of V̇_A/Q̇ ratio and provides an index of overall V̇_A/Q̇ mismatch as identified by the standard deviation of the distributions of ventilation and perfusion. This is calculated exclusive of shunt (considered to be V̇_A/Q̇ ratio < 0.005) and deadspace (V̇_A/Q̇ ratio > 100) with LogSDQ̇ designating heterogeneity in the perfusion vs. V̇_A/Q̇ ratio (log scale) and LogSDV̇ designating heterogeneity in the ventilation vs. V̇_A/Q̇ ratio (log scale).

Here, we evaluated the ability of single slice MRI measurements to characterize the V̇_A/Q̇ distribution in normal subjects by comparing MRI measures to those derived from MIGET. In addition, in this manuscript we report the implementation of measures applied to the imaging data that are expected to improve the measurement of regional V̇_A/Q̇ ratio in a single lung slice, including cross modality image registration and removal of large, conduit, vessels in perfusion images using a statistical clustering approach (39). The results of this study show that in healthy subjects MRI measures of V̇_A/Q̇ heterogeneity are closely related to those derived from MIGET.

METHODS

Subjects

The Human Subjects Research Protection Program of the University of California, San Diego, approved this study. A priori power calculations showed that given the expected variance in MIGET (8, 36) and MRI (17) the study of six subjects was expected to give a power of 0.8 to detect a significant relationship between MRI and MIGET measures of heterogeneity at P < 0.05, 2 tailed. Seven healthy volunteers (3 men, 4 women aged 23–63 yr) were recruited by advertisement and participated in this study after giving written informed consent. Each subject was screened using an MRI safety questionnaire and a medical history was taken. All subjects denied a history of significant illness, and in particular denied a history of pulmonary or cardiovascular disease. Spirometry was performed in the seated position using an EasyOne spirometer (NDD Medical Technologies. Zurich, Switzerland) to characterize pulmonary function to ensure that only those subjects with normal spirometry were included into the study. After undergoing the previously described preliminary screening, subjects underwent characterization of V̇_A/Q̇ distributions in supine posture on two separate days, approximately one week apart: one day using MIGET and another using proton MRI.

MIGET Study

Experimental setup.

The subjects were supine for the duration of the study. A radial artery cannula (20 gauge) was inserted under local anesthesia in the non-dominant arm for collection of arterial blood samples for measurement of respiratory gases and inert gas samples. In these resting studies blood temperature was estimated from the measured oral temperature. A peripheral venous cannula (20 gauge) was inserted in a forearm vein of the contralateral arm for infusion of the inert gas mixture (described below).

The subjects breathed through a mouthpiece connected to a Hans Rudolph (Shawnee, KS) non-rebreathing valve (model 2700), which in turn was connected to a heated (to prevent soluble gas loss) expiratory line and then to a heated mixing box. Expiratory ventilation and oxygen consumption were measured with a metabolic cart (Parvomedics Truemax; Parvo, UT). Subjects breathed through the mouthpiece for at least 10 min before inert gas sampling. For EKG monitoring and measurement of cardiac output, subjects were instrumented with a tetrapolar impedance cardiograph (model BioZ ICG; CardioDynamics, San Diego, CA). This device has been previously validated against direct Fick measures of cardiac output (42).

MIGET.

MIGET has been described many times in the literature and is only briefly outlined here (7). The six inert gases (sulfur hexafluoride, ethane, cyclopropane, enflurane, ether, and acetone) were placed into solution in sterile 0.9% sodium chloride solution and infused at a rate of 2–3 ml/min intravenously for 45 min before collection of the first samples. Mixed expired gas samples collected in duplicate, and a 6 ml arterial blood sample obtained in gas-tight glass syringes comprised a measurement set. Four such sets, i.e., 2 sets of duplicate pairs, were obtained. The concentrations of the inert gases in the gas and blood samples were measured using gas chromatography (model 5890A; Hewlett-Packard, Wilmington, DE) (27). Using the cardiac output measurements from the impedance cardiography and the arterial and mixed expired inert gas concentrations, mixed venous concentrations were calculated by the Fick principle. V̇_A/Q̇ distributions were obtained as follows: solubilities, retentions, and excretions for the inert gases were calculated and corrected for body temperature, before V̇_A/Q̇ distributions were calculated (22, 23). The standard deviation (log scale) of the perfusion distribution (the second moment, LogSDQ̇) excluding the shunt compartment and the second moment of the ventilation distribution, exclusive of dead space [LogSD of the ventilation distribution (LogSDV̇)] were used to quantify the extent of V̇_A/Q̇ mismatch. The residual sum of squares was used as an indicator of the adequacy of fit of the data to the 50-compartment model of the lung. The data derived from each of the 4 MIGET measurements (i.e., LogSDQ̇, LogSDV̇, residual sum of squares etc) were averaged after calculation for comparison with the MRI data.

Arterial sampling, blood gas measurements, metabolic data.

After each arterial blood sample used for the inert gas analysis, 2 ml of arterial blood was obtained, stored on ice and then analyzed with IL Synthesis-45 blood gas analyzer (Instrumentation Laboratories, Lexington, MA). Blood gas values were corrected to the body temperature. Arterial oxygen saturation was measured on the same samples using co-oximetry (IL682, Instrumentation Laboratories). The resulting data (i.e., Po_2, Pco₂, pH, and calculated AaDO₂) derived from each of the four arterial blood gas samples were averaged. Values of ventilation, oxygen consumption and carbon dioxide production were averaged over stable 2-min periods just before the inert gas sampling.

MRI Study

Experimental setup.

Subjects were positioned in the scanner in supine posture and MRI-compatible ECG electrodes (Invivo ECG Quadtrodes) were placed on the left chest. Subjects wore a facemask (7600 series Oro-nasal Mask, Hans-Rudolph) equipped with a non-rebreathing valve (2600 series, Hans Rudolph). Metabolic and ventilatory data were collected by connecting the expired side of the valve to a metabolic cart, identical to that used in the MIGET studies, located in the console room (Truemax 2400; Parvomedics, Sandy, UT).

A 1.5 Tesla Signa HDx TwinSpeed MRI system (General Electric Medical Systems, Milwaukee, WI) was used for image acquisition. Reference phantoms (silicone) were placed on the subject’s chest within the field of view providing a reference standard with known signal characteristics for absolute quantification of perfusion and lung density (see below). An eight-element torso coil (GE 8 channel cardiac array coil, General Electric Medical Systems) was then placed around the subject’s chest for acquisition of the pulmonary blood flow and specific ventilation images. Proton density images were collected using both the body coil built into the scanner and the torso coil. This dual acquisition of density scans allowed construction of a coil sensitivity profile, as described below. Data were acquired in a 15 mm sagittal slice located in the mid-clavicular line of the right lung thus providing the greatest AP distance and the maximum volume of lung. The subject was trained to gate respiration for pulmonary blood flow and specific ventilation images (described below) so that each image was acquired at functional residual capacity (FRC).

Proton density imaging.

Regional proton density was measured during a 9-s breath-hold at FRC using a fast gradient echo sequence developed in house as reported in (34). This sequence acquires multiple single echo acquisitions consisting of 12 images alternating between two echo times in a single 9-s breath-hold. These twelve images are comprised of six “even” images (i.e., images 2, 4, 6, 8, 10, 12) acquired at a short echo time of 1.1 ms and six “odd” images (images 1, 3, 5, 7, 9, 11) at a longer echo time of 1.8 msec. The short echo time of 1.1 ms is the minimum permitted by the sequence parameters which were TR = 10 msec, flip angle = 10 degrees, slice thickness = 15 mm, field of view = 40 cm, receiver bandwidth = 125 kHz, and a full acquisition matrix of 64 × 64. The first 4 images are discarded because they have been previously determined to not represent steady state (34). A proton density image is then constructed by fitting a single exponential on a voxel-by-voxel basis from the last eight images, four for each of the two different echo times, and back-extrapolating to determine the magnetization at time zero (34). Absolute quantification is obtained by comparing the result against a reference phantom of known properties. This technique for quantifying regional lung water content/proton density has been validated, showing a high correlation between measured MRI water content and gravimetric water content with R² = 0.95, P < 0.0001 and excellent reliability (20). A second set of proton density images were collected with the torso coil to create a coil sensitivity profile used in quantification of the perfusion images (16) as briefly outlined below.

Specific ventilation imaging.

Oxygen delivered to and dissolved into lung tissues shortens the longitudinal relaxation time (T₁) (9, 11), increasing the local MRI signal intensity in a T₁-weighted inversion recovery image. Specific ventilation imaging (SVI) takes advantage of this to measure the wash-in/wash-out time constant, on a voxel-by-voxel basis, following a sudden change in inspired oxygen concentration (fractional inspired oxygen, or $\mathrm{F}{\mathrm{I}}_{{\mathrm{O}}_{\mathrm{2}}}$). The amount of locally dissolved oxygen depends on local availability, which in turn is determined by specific ventilation—the ratio of fresh gas entering a lung region divided by its end-expiratory volume. Following a sudden change of inspired $\mathrm{F}{\mathrm{I}}_{{\mathrm{O}}_{\mathrm{2}}}$, voxels that have a high specific ventilation reach the new equilibrium quickly whereas regions with a low specific ventilation take more time. Thus, the time delay between the change in inspired gas concentration and the response of a particular voxel showing the increase and decrease in signal intensity is uniquely determined by specific ventilation (32). To translate the time for the change in the MRI signal into a specific ventilation we previously constructed a model of a lung unit corresponding to the voxel size measured during the MRI imaging as reported in (32).

Regional specific ventilation was measured as described in (32) by acquiring T₁-weighted images at FRC while the subject was breathing air, followed by breathing 100% oxygen, in alternating 20 breath cycles; five air-oxygen cycles were acquired for robustness; an additional block of 20 breaths while breathing 100% oxygen is added at the end, to increase the ability to quantify slower equilibrating units.

The two-dimensional T₁-weighted images required for SVI were acquired with an inversion recovery single-shot fast spin echo (SSFSE) sequence with a 40 × 40-cm field of view, echo time of ∼30 ms, and a 15-mm image slice thickness. A TI of 1,100 ms was chosen because it maximizes the sensitivity (contrast) to changes between air and oxygen breaths (9). A half-Fourier single-shot turbo spin echo (HASTE) acquisition of a 256 × 128 Fourier space was used for data acquisition. A homodyne reconstruction algorithm was then applied to reconstruct the data to a 256 × 256 matrix, resulting in a voxel size of ∼1.6 × 1.6 × 15 mm (∼40 mm³). The specific ventilation imaging technique shows good test-retest reliability and has been recently validated against a multiple breath washout technique with good results (31).

Measuring pulmonary blood flow using ASL.

Regional pulmonary blood flow was assessed using 2D arterial spin labeling (ASL) with a flow-sensitive alternating inversion recovery with an extra radiofrequency pulse (FAIRER) imaging sequence and a Half-Fourier Acquisition Single-shot Turbo spin-Echo (HASTE) data collection schema (4, 25). This has been described in detail (4, 21) and used in a number of studies by our group (15, 21) and is only briefly described here.

Arterial spin labeling “tags” protons using radiofrequency and spatial magnetic field gradient pulses (4, 25, 26) and allows those in flowing blood to be used as endogenous tracer. An ASL measurement consists of pairs of images in a lung slice acquired at FRC. The pairs differ in how the pulses are applied: in one, a spatially selective inversion (180°) pulse is applied to the section being imaged during diastole. This means that protons outside the imaged section are not affected. This is the “control” image, acquired after a delay of 80% of one R-R interval (the time interval from R wave from one QRS complex to the R wave of the next), so that a single systolic cycle has taken place. When tipped over to create an image, the longitudinal magnetization of the protons outside the image generate a magnetic resonance signal in the image if they are transported to the image plane in flowing arterial blood during the systolic cycle. In the second image, a spatially non-selective inversion (180°) pulse is applied to the whole lung, and all the protons in the thorax both intravascular and extravascular are affected. This is the “tagged” image. As for the “control” image, the “tagged” image is subsequently acquired after a delay of 80% of one R-R interval. During this delay, blood flows into the imaged slice, with strong signal in the case of the control image and little signal in the case of the tag image, with relaxation of the magnetization in both. The two images are then subtracted and the difference between the two for each voxel reflects the amount of blood delivered during the delay between application of the inversion and acquisition of the image, weighted by a decay factor due to the relaxation of the blood magnetization during that interval (16). This technique has been validated in a lung phantom model (22) and shows excellent reliability (24).

Imaging sequence parameters were as follows: TI = 600–800 ms (based on subject’s heart rate), TE = 21.3 ms, field of view = 40 cm, slice thickness = 15 mm. The collected image matrix size was 256 × 128 (reconstructed by scanner to 256 × 256) giving voxels of 0.156 × 0.156 × 1.5 cm, or ~0.037 cm³. The HASTE imaging sequence had an inter-echo time of 4.5 ms and 70 lines of phase encoding, resulting in a data acquisition time of 324 ms.

Combined ASL-SVI sequence.

For one subject, the ASL and SVI images were acquired in succession. In the remaining 6 subjects we took advantage of a pulse sequence modification that allowed the measurements of regional pulmonary blood flow and specific ventilation (as described above) to be merged into a single imaging sequence to facilitate imaging of ventilation and blood flow in a single acquisition. It should be noted that the underlying data acquisition was not significantly modified with this change. Subjects performed the same 5 cycles alternating between 20 breaths of room air and 20 breaths of 100% oxygen as part of specific ventilation imaging. In each block of 20 breaths, 18 inversion recovery images were acquired (for specific ventilation imaging) and a pair of ASL images was acquired on breaths 17 and 18 for measurement of pulmonary blood flow, a position in the O₂/Air cycle shown to minimize the error of measurement of specific ventilation. The entire combined measurement took ~18 min to complete. To prevent an effect on the perfusion distribution from the hyperoxia used in the ventilation part of the combined sequence, only the 5 tag/control pairs of ASL images acquired during the normoxic portion of the combined sequence were used for quantification of perfusion.

Image Processing

Creation of coil sensitivity profiles.

To determine the spatial inhomogeneity of the coil sensitivity, the proton density images acquired using both the torso coil and the body coil were used (16). The two average torso and body coil short echo time original magnitude images were spatially smoothed by applying a 2D Gaussian low-pass filter in frequency space, equivalent to convolving with a 2D Gaussian in image space with standard deviation of 3.4 voxels (2.1 cm) and full width at half maximum of 8 voxels (5 cm). The resultant smoothed images were divided (torso/body) to define the individual coil sensitivity map for each subject.

Regional lung density.

Typically, three body coil density maps were acquired for each subject; images were displayed side by side, and a representative image selected, as judged by consistent lung volume (number of voxels). The proton density image collected using the body coil was normalized to the signal derived from the silicone phantom to obtain regional lung proton (water) density in units of grams H₂O per milliliter of lung (34).

Quantification of ventilation.

Specific ventilation image analysis was performed as previously described (32) with some small differences. The time series of 220 images corresponding to the SVI or SVI/ASL sequence was imported into Matlab (Mathworks, Natick, MA), visually inspected and images where the subject was clearly not at FRC were discarded. To ensure optimum data quality, images were registered using a custom designed image registration algorithm, using a projective transformation based on the boundaries of the lung ROI (1). Any image that required deformation greater than 10% (area change) was eliminated from the analysis as our registration algorithm was shown to be accurate up to ~10–12% lung deformation (2), typically resulting in the elimination of fewer than 5 images out of the 220. ASL tag and control pairs were removed for separate analysis. Those images and discarded SVI images were replaced by the average of the previous and following available SVI images. SVI quantification was performed as described in full in (31). In short, the time series of each voxel in the lung ROI was compared with a library of simulated responses for 50 idealized lung units with specific ventilation in the range 0.01 to 10, when presented with the imposed $\mathrm{F}{\mathrm{I}}_{{\mathrm{O}}_{\mathrm{2}}}$ driving function. The correlation between individual voxels time course in response to the challenge and the 50 simulated SV was used to determine the specific ventilation of each voxel. The null hypothesis of no correlation was rejected at a P < 0.05. Voxels for which the null hypothesis was not rejected, and SV quantification was not possible, were treated as missing data (typically ~1% of voxels in the ROI). The ability of specific ventilation imaging to quantify SV > 1 is limited (31, 32), and these regions likely correspond to airways or well ventilated spaces. Therefore, similarly to what was performed for large conduit vessels, a binary mask was applied to exclude regions with SV > 1, from further analysis (ventilation and ventilation-perfusion images).

To calculate alveolar ventilation from specific ventilation, the ratio of the delivery of fresh air (alveolar ventilation) to resident air (local FRC) in a voxel, voxels were assumed to be composed of two binary compartments of air elements and non-air elements. Furthermore, we assumed that the proton density measurements accurately captured the non-air compartment. Following registration of the specific ventilation and lung density images using normalized cross-correlation in MATLAB, alveolar ventilation in ml/min/ml was calculated on a voxel-by-voxel basis as the product of specific ventilation, the volume fraction of air (1 – lung density), and the frequency of breathing.

Regional blood flow.

The ASL image pairs acquired while breathing air were registered as above, subtracted and inspected for image quality, consisting of absence of mis-registration between images, diaphragm movement or artifacts related to improper cardiac gating. The first image of those that met the criteria was selected. This image was quantified by referencing the signal to the mean signal in the calibration phantom (T₁ 620 ms, T₂ of 160 ms) and the T₁ and T₂ of the phantom relative to assumed values for human pulmonary arterial blood (33). From this, blood delivered in units of milliliters per minute per millilter of lung (averaged over one cardiac cycle) was calculated (16) for each ASL image. These ASL images, which were obtained using the torso coil were then divided by the coil sensitivity profile for each subject, on a voxel-by-voxel basis (16) in order to obtain a quantitative map of blood delivered to the image, independent of the spatial variations in coil sensitivity. This image contains signal from both perfusion and also from large “conduit” vessels (see below).

Quantification of regional perfusion.

In an ASL image acquisition in the lung, all protons delivered from outside the tagging band into the imaging slice in one R-R interval contribute to the measured signal. This is not true perfusion since it includes blood flow in larger “conduit” vessels that do not feed the local capillary beds (6). To deal with this issue, we applied a statistical clustering approach to discriminate between perfusion and conduit vessels as we have recently described (39). The data-driven clustering technique is based on a Gaussian mixed model approach, applied to voxel-by-voxel 2-dimensional X-Y scatter plot of the ASL data, coil sensitivity corrected, blood-dark (x-axis) and blood-bright (y-axis) image pairs. The coil corrected blood-dark and blood-bright images are, for the sake of clustering, treated as independent measurements. Large, conduit vessels and perfused lung regions show distinct, separable behaviors, when analyzed as a Gaussian mixture model. In a log-log X-Y plot, this is reflected as follows: the large vessel (conduit vessel) cluster has a higher slope (higher signal increase from the blood-dark to blood-bright image) than the perfusion cluster. Clustering is done by identifying two log-normal voxel clusters, corresponding to perfusion and large vessels using an iterative expectation maximization algorithm. Each voxel is attributed a posterior probability of belonging to each cluster. The binary mask associated with large vessels was created by setting a conservative threshold, assigning voxels with P > 0.2 likelihood of being large vessels (<0.8 of being perfusion) to the large vessel category. Voxels assigned to the perfusion cluster were retained and analyzed, while voxels contained in the binary mask of the lung region of interest corresponding to larger conduit vessels were excluded from the perfusion analysis. Voxels containing larger conduit blood vessels were also excluded from calculated ventilation-perfusion images.

Blood flow and ventilation image registration, smoothing and quantification of V̇_A/Q̇ ratio.

Alveolar ventilation and perfusion images were co-registered using deformable image registration (projective deformation, based on the lung boundary (2) in MATLAB. Using the set of density images as the basis for registration, a region of interest (ROI) identifying the lung was drawn, and the density images were registered, if required. Typically, as the density images are acquired during a breath hold at FRC, no registration is required within the 12 images acquired in a density set, or across repetitions of the density scan. The selected ROI is then used as an input (reference ROI) in the registration of the SVI-ASL image set; the advantage of this approach is that it will result in co-registration across modalities, bringing all the images, quantitative maps and coil sensitivity profile into a common space.

Images were smoothed by convolving them with a Gaussian kernel low pass filter (with a full width half maximum of 5 voxels), applied in the frequency domain, effectively giving the smoothed lung density, ventilation, perfusion, and V̇_A/Q̇ ratio images a resolution of ~1 cm³. The smoothing algorithm used the lung mask, excluding voxels outside the lung, voxels identified as large conduit vessels, and voxels with high specific ventilation. The Gaussian weights for averaging the lung voxels were adjusted to account for removal of the masked voxels, treating them as missing data. Regional V̇_A/Q̇ ratio was defined as the ratio of the smoothed ventilation (calculated from the specific ventilation and density images, ml/min/ml) and smoothed perfusion (ml/min/ml) images on a voxel-by-voxel basis.

Data Analysis

The mean and standard deviation of smoothed regional density (g/ml), ventilation (ml/min/ml), perfusion (ml/min/ml), and V̇_A/Q̇ ratio (dimensionless) were calculated for a region of interest encompassing the lung in the sagittal image. The total ventilation and perfusion to the imaged slice was calculated as the sum of the individual voxel values for the retained alveolar ventilation and perfusion.

The second moments (on a log scale) of the ventilation (LogSDV̇) and perfusion (LogSDQ̇) vs. V̇_A/Q̇ ratio distributions, which are both measures of the extent of V̇_A/Q̇ heterogeneity and analogous to those derived from the multiple inert gas elimination technique (37), were also calculated as described in Henderson et al. (17). Essentially a cumulative plot of V̇ (or Q̇) vs. V̇_A/Q̇ ratio was sampled at 50 compartments, equally spaced on a logarithmic scale. The 50 compartments spanned V̇_A/Q̇ ratios of 0.005 to 100, with compartment 1 including all voxels with V̇_A/Q̇ <0.005 and compartment 50 those voxels with V̇_A/Q̇ ratio >100, as for MIGET. From these histograms, the second moments V_A2 and Q₂ were calculated as:

$${\dot{V}}_{A2}=\frac{{\displaystyle \sum \left({\dot{V}}_A\cdot {\left[\ln ({\dot{V}}_{A1})-\ln \left(\frac{{\dot{V}}_A}{\dot{Q}}\right)\right]}^2\right)}}{{\displaystyle \sum {\dot{V}}_A}}$$

$${\dot{Q}}_2=\frac{{\displaystyle \sum \left(\dot{Q}\dot{}{\left[\ln ({\dot{Q}}_1)-\ln \left(\frac{{\dot{V}}_A}{\dot{Q}}\right)\right]}^2\right)}}{{\displaystyle \sum \dot{Q}}}$$

LogSDV̇ and LogSDQ̇ were then calculated as the square root of V̇_A2 and Q̇₂.

Statistical Analysis

The researchers analyzing the MIGET data (H. Wagner, A. C. Henderson) and the researcher analyzing the MRI data (R. C. Sá) were each blinded to the other data set during data analysis. Data were tested for normality using a Shapiro-Wilk Test, and were not significantly different from a normal distribution. Metabolic and ventilatory data were compared between the two study days using a paired t-test. We compared V̇_A/Q̇ heterogeneity measured by MRI to that measured using MIGET using linear regression (Statview 5.0, SAS, Cary, NC). A Bland-Altman analysis (3) was used to determine bias [or mean error; calculated as (value MRI- value MIGET)/n-1] and the confidence interval (SD of value MRI-value MIGET; the smaller the SD, the greater the agreement between the two techniques) were calculated for LogSDV̇ and LogSD Q̇. Prediction limits of 95% for the MRI LogSDV̇ and LogSDQ̇ as a function of MIGET measured LogSDV̇ and LogSDQ̇ were generated. All data are presented as means ± SD, the null-hypothesis (no effect) was rejected for P < 0.05, two tailed.

RESULTS

All subjects tolerated the study well. Subject physical characteristics and spirometry data are given in Table 1. All subjects had spirometry that was within normal limits. Metabolic data obtained during MRI and MIGET are given in Table 2. There were no significant differences between measurement days for oxygen consumption, carbon dioxide production or respiratory exchange ratio indicating similar conditions of measurement between the two study days (Table 2). Arterial oxygen saturation was normal, but was significantly different between the two measurement days (P = 0.04), This likely represents differences between pulse oximetry (used in the MRI studies) and the saturation measured with co-oximetry.

Table 1.

Subject demographics

Subject	Sex	Age, yr	Height, cm	Weight, kg	FVC, liters	FVC, %	FEV1, liters	FEV1,%
1	F	55	173	81.8	3.82	97	3.12	101
2	F	55	180	88.2	4.46	88	3.16	81
3	M	24	185	90.9	5.28	87	4.57	92
4	F	63	163	52.7	2.49	82	2.1	88
5	M	23	175	65.9	5.72	106	4.21	94
6	F	42	160	54.5	3.06	86	2.72	94
7	M	31	170	63.6	5.27	105	4.42	107
Mean		42	172	71.1	4.30	93	3.47	94
± SD		16	9	15.8	1.22	10	0.94	8

FVC , forced vital capacity; FVC %, percent of predicted forced vital capacity; FEV₁, forced expiratory volume in 1 s; FEV₁%,  percent of predicted forced expiratory volume in 1 s.

Table 2.

Metabolic data (mean ± SD) during the multiple inert gas elimination technique (MIGET) and magnetic resonance imaging (MRI) experiments

	MIGET	MRI	P
V̇E, l/min BTPS	7.92 ± 0.88	7.16 ± 1.00	0.08
V̇o2, l/min STPD	0.24 ± 0.04	0.24 ± 0.03	1.00
V̇o2, ml/kg/min	3.5 ± 0.8	3.5 ± 0.4	0.81
V̇co2, l/min STPD	0.21 ± 0.03	0.20 ± 0.03	0.70
RER	0.87 ± 0.05	0.84 ± 0.05	0.26
$\mathrm{S}{\mathrm{a}}_{{\mathrm{O}}_{\mathrm{2}}}$, %	98.3 ± 0.8	97.1 ± 1.4	0.04

V̇E, minute ventilation; V̇o₂, oxygen consumption; V̇co₂, carbon dioxide production; RER, respiratory exchange ratio; $\mathrm{S}{\mathrm{a}}_{{\mathrm{O}}_{\mathrm{2}}}$, arterial oxygen saturation measured by pulse oximeter (MRI) or co-oximeter (MIGET); STPD, standard temperature pressure dry; BTPS, body temperature pressure saturated.

Arterial Blood Gases

Arterial blood gas data and the calculated ideal alveolar-arterial partial pressure difference for oxygen (AaDO₂) for each subject is given in Table 3. Six of the seven subjects had a normal A-aDO₂ for their age, indicating normal gas exchange (8). However, one subject, Subject 2, had a larger than normal AaDO₂. This was because of a ~6% shunt measured by MIGET (See below, Table 4). One subject, Subject 4, hyperventilated markedly during the MIGET study and had low Paco₂ and alkaline blood pH during the study. This acute alteration in ventilation is not expected to substantially affect measures of V̇_A/Q̇ heterogeneity, either from MRI or MIGET.

Table 3.

Arterial blood gas data during the MIGET experiments

Subject	$\mathrm{P}{\mathrm{A}}_{{\mathrm{O}}_{\mathrm{2}}}$,Torr	$\mathrm{P}{\mathrm{a}}_{\mathrm{O}}{}_{{}_{\mathrm{2}}}$, Torr	AaDO2, Torr	$\mathrm{P}{\mathrm{a}}_{\mathrm{C}\mathrm{O}}{}_{{}_{\mathrm{2}}}$, Torr	pHa
1	101	82	19	42.6	7.39
2	107	80	27	33.5	7.42
3	109	109	0	36.7	7.43
4	119	104	15	25.5	7.51
5	106	97	9	38.3	7.41
6	113	111	2	33.3	7.44
7	104	96	8	41.9	7.37
Mean	108	97	11	35.9	7.42
± SD	6	12	10	5.9	0.05

$\mathrm{P}{\mathrm{A}}_{{\mathrm{O}}_{\mathrm{2}}}$, calculated ideal alveolar partial pressure of oxygen; $\mathrm{P}{\mathrm{a}}_{\mathrm{O}}{}_{{}_{\mathrm{2}}}$, arterial partial pressure of oxygen; AaDO₂, alveolar-arterial difference for oxygen; $\mathrm{P}{\mathrm{a}}_{\mathrm{C}\mathrm{O}}{}_{{}_{\mathrm{2}}}$,  arterial partial pressure of carbon dioxide; pHa , arterial pH.

Table 4.

MIGET data

Subject	RSS	Q̇ Shunt, %	V̇ Dead	Mean Q̇	LogSDQ̇	Mean V̇	LogSDV̇
1	6.06	0.50	0.41	0.78	0.51	1.04	0.57
2	6.33	6.38	0.42	0.58	0.54	0.78	0.53
3	7.07	0.00	0.42	0.89	0.34	1.00	0.34
4	9.01	0.68	0.33	1.16	0.41	1.38	0.41
5	8.21	0.33	0.43	0.86	0.32	0.96	0.32
6	5.30	0.40	0.28	0.90	0.50	1.15	0.51
7	7.78	0.35	0.41	0.82	0.39	0.96	0.39
Mean	7.11	1.23	0.38	0.86	0.43	1.04	0.44
± SD	1.30	2.28	0.06	0.17	0.09	0.19	0.10

RRS, residual sum of squares; Q̇ shunt, percent of cardiac output to regions of shunt (V̇_A/Q̇ < 0.005); V̇ Dead, fraction of ventilation to dead space (V̇_A/Q̇ > 100); mean Q̇, the mean of the perfusion distribution; LogSDQ̇, the standard deviation log scale of the perfusion vs. V̇_A/Q̇ distribution, an index of V̇_A/Q̇ heterogeneity; mean V̇ the mean of the ventilation distribution, LogSDV̇ the standard deviation log scale of the ventilation vs. V̇_A/Q̇ distribution, an index of V̇_A/Q̇ heterogeneity.

MIGET Data

Data from the MIGET experiment are given in Table 4. The residual sum of squares averaged 7.11 ± 1.30 indicating adequate fit of the data to the 50-compartment model. All of the subjects had a normal amount of deadspace (38 ± 6%) (29). It should be noted that the deadspace measured by MIGET includes not only physiologic deadspace (i.e., anatomic deadspace and alveolar deadspace) but also deadspace in the body of the Hans-Rudolph non-rebreathing valve. The subjects had V̇_A/Q̇ distributions that were unimodal and the measures of V̇_A/Q̇ heterogeneity, the LogSDQ̇ and LogSDV̇ were within normal limits for the subject’s ages (8). The MIGET data were highly reliable with a correlation between duplicate pairs of 0.94 for LogSDQ̇ and 0.87 for LogSDV̇, consistent with previously published data (36). As mentioned above, Subject 2 had an elevated shunt fraction, consistent with the lower than normal Pao₂ and elevated A-aDO₂ seen in the arterial blood gas data.

MRI Data and MIGET MRI Comparison

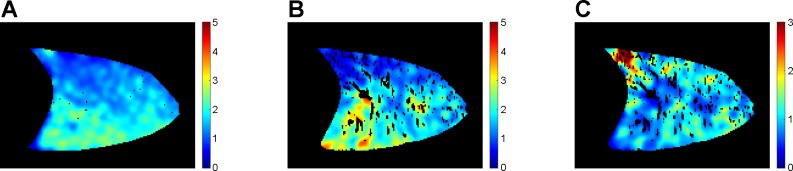
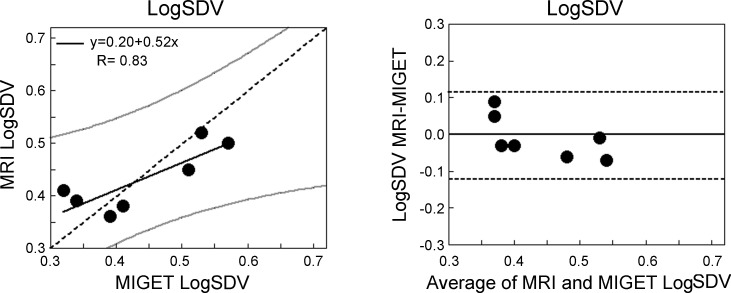
Example images of density, alveolar ventilation, perfusion, and V̇_A/Q̇ ratio for a subject are shown in Fig. 1, and a comparison of the recovered distributions from MRI and MIGET for this subject is given in Fig. 2. Figure 3 shows MRI/MIGET comparisons for the remaining six subjects. Figure 4A shows the regression of the LogSDV̇ derived from MRI compared with that from MIGET, and Fig. 4B shows the Bland-Altman plot. The MRI LogSDV̇ was closely correlated with MIGET (R = 0.83, P = 0.02) but the intercept differed significantly from zero (intercept = 0.20, P = 0.04) and the slope deviated significantly from identity (slope = 0.52, P = 0.01). Averaged over the subject group, the MRI LogSDV̇ was not significantly different than the MIGET value (MRI = 0.43 ± 0.06, MIGET = 0.44 ± 0.10, P = 0.70) with an average bias of −0.01 and a precision of 0.03.

Fig. 1.

Example images of alveolar ventilation (A), perfusion (B), and V̇ _A/Q̇. ratio (C) in a sagittal slice of the right lung in a normal subject (subject 7) in the supine posture. Color scale for ventilation and perfusion in A and B is in units of ml/min/ml of lung. For C it is the dimensionless V̇_A/Q̇ ratio. Dark areas within the images correspond to voxels that do not correlate with the driving function or have a specific ventilation > 1 in image A, to regions of the lung corresponding to large vessels in B, and to both uncorrelated voxels and large vessels in image C.

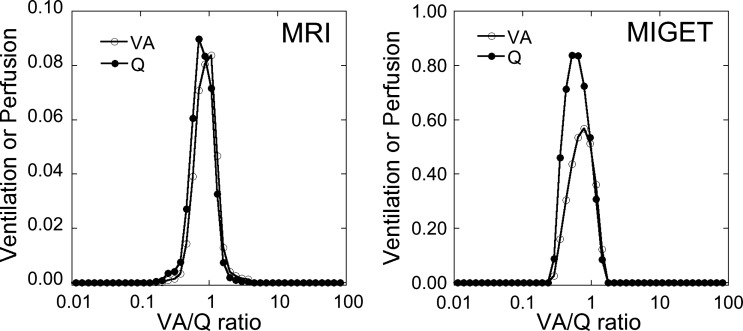
Fig. 2.

Recovered V̇_A/Q̇ distributions from MRI (A) and MIGET (B) from the subject shown in Fig. 1. The scale for the y-axis for MRI data is ~10% that of MIGET because MIGET data are for the whole lung whereas the MRI data are for a single slice only.

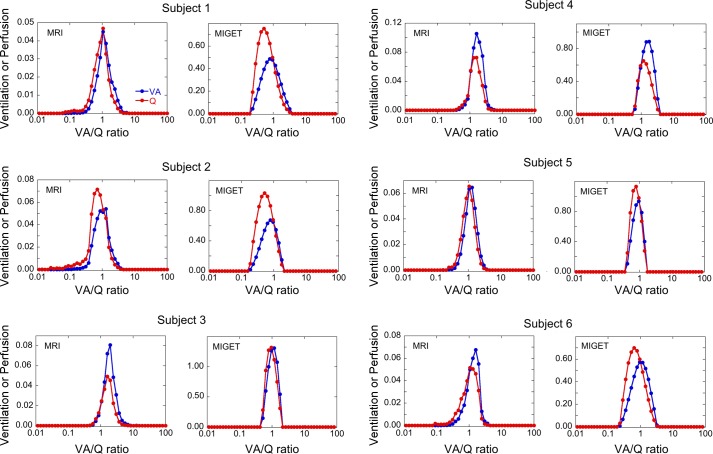
Fig. 3.

Recovered V̇_A/Q̇ distributions from MRI and MIGET from six subjects with MRI on the left and MIGET on the right of each pair. The scale of the y-axis varies between individuals and between MRI and MIGET because it is dependent on total alveolar ventilation and cardiac output for the individual subject as well as the volume of lung sampled in MRI. The volume of lung in the MRI images is ~8% of the total lung.

Fig. 4.

Left: the regression of the LogSDV̇ derived from MRI compared with that from MIGET. The two measures were well correlated (R = 0.83, P = 0.02). Dotted line is the line of identity, gray lines are the 95% confidence limits for the relationship. The slope of the relationship was significantly different from the line of identity (P = 0.01) and the intercept was also significantly different from zero (P = 0.02). Right: the corresponding Bland-Altman plot. Dotted lines are the 95% confidence limits. The average bias between techniques was −0.01.

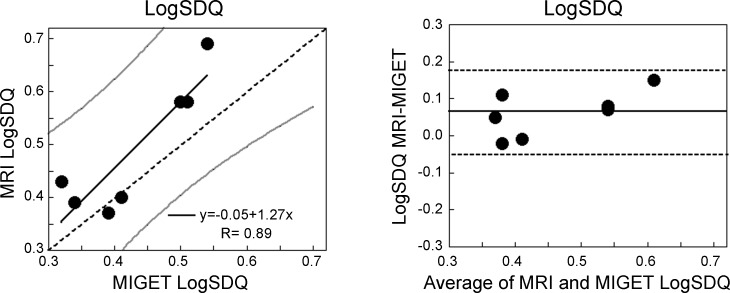
Figure 5A shows the regression of the LogSDQ̇ derived from MRI to that from MIGET, and Fig. 5B shows the Bland-Altman plot. The MRI LogSDQ̇ was highly correlated with the MIGET value (R 0.89, P = 0.007) and the slope was not significantly different from the line of identity (slope = 1.29, P = 0.34) nor did the intercept differ significantly from zero (intercept = −0.062, P = 0.65). Averaged over the seven subjects the MRI LogSDQ̇ was significantly greater than the MIGET value (MRI = 0.49 ± 0.12, MIGET = 0.43 ± 0.09, P = 0.04) with an average bias of 0.06 and a precision of 0.05.

Fig. 5.

Left: the regression of the LogSDQ̇ derived from MRI compared with that from MIGET. The two measures were well correlated (R = 0.89, P = 0.007). Dotted line is the line of identity, gray lines are the 95% confidence limits for the relationship. The slope of the relationship is not significantly different from the line of identity (P = 0.34) and the intercept is also not significantly different from zero (P = 0.65). Right: the corresponding Bland-Altman plot. Dotted lines are the 95% confidence limits. The average bias between the techniques was 0.06.

DISCUSSION

The results of the current study show that in these 7 normal subjects, MRI measures of V̇_A/Q̇ heterogeneity closely correspond to those derived from MIGET and the degree of association between MRI and MIGET measures of LogSDV̇ and LogSDQ̇ are similar to the strength of association between duplicate pairs of MIGET measurements (36). MIGET (18, 19, 30, 38) is a useful quantitative technique that evaluates pulmonary gas exchange, by measuring the concentrations of trace amounts of six inert gases physically dissolved in saline and infused intravenously, in arterial, expired and mixed venous blood. The relative amount of gas retained in blood and excreted in expired gas is used to solve for the distribution of V̇_A/Q̇ ratio in multiple gas exchange units. MIGET quantifies the distributions of ventilation and perfusion to be expressed as a function of V̇_A/Q̇ ratio (see Fig. 2). Despite being well established, and widely used in research for measuring ventilation-perfusion inequality, MIGET has never been broadly clinically implemented. This is likely because MIGET is time consuming, technically difficult, and invasive, limiting the application of MIGET.

Recently, our group reported the use of functional lung imaging with proton MRI to quantify regional V̇_A/Q̇ ratio (17). This MRI method combines lung density and specific ventilation measurement to calculate regional alveolar ventilation, which combined with regional blood flow measurements allows local V̇_A/Q̇ ratio to be measured in a single lung slice. In this prior study (17), LogSDQ̇ and LogSDV̇ were calculated from the second moments (on a log scale) of the perfusion and ventilation vs. V̇_A/Q̇ ratio distributions generated from the ventilation, perfusion, and regional V̇_A/Q̇ ratio images, and were remarkably similar to the values reported for similar populations of young subjects measured using the multiple inert gas elimination technique (37). In the present manuscript we have extended this work to compare the MRI measures of V̇_A/Q̇ heterogeneity against MIGET in a small population of normal subjects, and the data show that, in this limited volumetric interrogation of the lung with our imaging technique, that MRI measures of LogSDV̇ and LogSDQ̇ correlate well with those derived from MIGET. However, the MRI measures of LogSDQ̇ were significantly greater than those derived from MIGET (on average by 0.06) whereas the MRI measures of LogSDV̇ had a slope significantly different from the line of identity, and a non-zero intercept but with no net bias. As discussed below this may be related to the small number of subjects studied, or may indicate a limited sensitivity of the MRI technique to evaluate the LogSDV̇.

Our study population spanned age ranges from 23 to 63 and all of our subjects had V̇_A/Q̇ heterogeneity that was within the normal physiological range (8) when the subject’s age was taken into account. V̇_A/Q̇ heterogeneity is known to increase with age, albeit with substantial variability and there is a modest correlation between LogSDQ̇ and LogSDV̇ and age (R = 0.25 and 0.35 respectively) (8). Consistent with this, we found relationships between both LogSDQ̇ and LogSDV̇ from both MRI and MIGET and subject age in our subject population, but these did not reach statistical significance, likely because of the small number of subjects. Correlations were R = 0.73 and 0.72 for MIGET LogSDQ̇ and LogSDV̇ (P = 0.06 and 0.07) and 0.51 and 0.48 for MRI LogSDQ̇ and LogSDV̇ (P = 0.25 and 0.27).

For reasons that are unclear, one subject had an abnormal amount of shunt which was ~6% of cardiac output. This subject had a normal medical history and spirometry. Since the shunt compartment (as is the deadspace compartment) is separate from the remaining V̇_A/Q̇ ratio compartments used in calculations of LogSDV̇ and LogSDQ̇, we elected to retain these data. The source of this individual’s shunt may have arisen from a right to left intracardiac or an intrapulmonary shunt. At the present time we are not able to quantify the extent of shunt with MRI and the reasons for this are discussed below.

Possible Reasons for Discrepancies Between MRI and MIGET

Small sample size.

It is important to note that overall the correspondence between the two techniques was significant indicating good agreement. However, we found a systematic bias in the LogSDQ̇ data, whereby the numbers derived from MRI indicated more heterogeneity than MIGET. Additionally, for LogSDV̇ the slope of the relationship was such that MRI tended to overestimate LogSDV̇ relative to MIGET at low values and underestimate it at higher values. Given the small number of subjects studied it is important not to over interpret the differences or similarities between measures of V̇_A/Q̇ heterogeneity from MRI and MIGET. Random experimental noise in both techniques combined with a small number of subjects could in part explain the discrepancy, or alternately explain the extent of agreement between the two techniques that we found.

Smoothing and assumptions.

The two techniques in the present study use vastly different approaches to derive metrics that reflect V̇_A/Q̇ matching. MIGET uses data derived from gas exchange that is fit to a 50 compartment model with a number of imposed constraints on the model fitting, based on reasonable assumptions about gas exchange. In particular, the smoothing factor Z, imposes constraints on MIGET that differ from those imposed on MRI. Smoothing stabilizes the recovered V̇_A/Q̇ distribution in the presence of random experimental errors for both MRI and MIGET. In MIGET, the smoothing factor Z is applied to MIGET data as part of deriving the 50 compartment model; this constraint limits the number of modes that can be recovered (three) and imposes a lower limit of heterogeneity that can be resolved (LogSDQ̇ ~0.3) (13).

The MRI measures of V̇_A/Q̇ heterogeneity are subject to an entirely different set of assumptions that are largely related to the physics of image acquisition, and other assumptions related to image processing. These assumptions include those made to eliminate large, conduit vessels (not representing blood flow, see below) in the perfusion images and to eliminating voxels that either do not correlate or correspond perfectly with the driving function in the specific ventilation images. For the MRI data smoothing is applied before the individual images that form the composite V_A and V̇_A/Q̇ map are combined. Once the composite V̇_A/Q̇ image is obtained this is output as a histogram with 50 equally spaced compartments, and the second moment of the distribution computed, like MIGET, excluding the deadspace (V̇_A/Q̇ ratio >100) and shunt (V̇_A/Q̇ ratio <0.005) compartment. Thus differences in assumptions might play a role in the discrepancies: Since smoothing dictates the number of modes that can be distinguished with MIGET (maximum of three modes) and spatial smoothing in MRI has the effect of reducing apparent heterogeneity, this may bias the results from the two techniques in a complex manner. This effect is expected to be small in normal lungs, where the distribution is expected to be relatively uniform and unimodal, but may be more important in the abnormal lung.

Spatial scale.

Heterogeneity is a function of the scale at which it is measured: Under a microscope, the colors of individual grains of sand can be discerned; at 10,000 feet the beach may appear a uniform color. The functional resolution that corresponds to the 50 compartment model of gas exchange that is used in MIGET is one acini (41). MRI data have a known spatial resolution that is to a large extent fixed: coarser resolution is possible but finer resolution is not. As currently implemented the spatial resolution of our MRI technique after processing roughly corresponds to ~1 cm³ or ~5–6 acini. The resolution of our measurements may cause an underestimation of the extent of heterogeneity compared with MIGET. Whether this is the explanation for the underestimation of LogSDV̇ measured by MRI compared to MIGET at the lower end of the range of values is unknown. Since ventilation, perfusion and V̇_A/Q̇ ratio are spatially clustered (14) the functional resolution of our MRI technique is likely adequate to reflect the heterogeneity present in the normal lung.

Effects of random experimental noise.

No experimental technique is without noise and random experimental noise affects the two techniques differently. As discussed above the smoothing factor, Z, stabilizes the recovered V̇_A/Q̇ distributions from MIGET, albeit at the expense of not being able to discriminate distributions with very low heterogeneity and distributions with multiple modes close together in the V̇_A/Q̇ range. In MIGET, each compartment is weighted by its V̇_A/Q̇ ratio. This is because when blood flow to a compartment is low, small differences in flow result in large differences in the associated V̇_A vs. V̇_A/Q̇ ratio, and this is not the case in the MRI data. This may in part explain some of the differences we observed in the slope of the relationship between LogSDV̇ derived from MRI and that from MIGET. The effect of noise on our MRI measure of regional specific ventilation is more likely to broaden the specific ventilation distribution than make it narrower, by lowering the correlation with all modeled responses and thus potentially erroneously assigning a voxel response to a different modeled time course. Increasing the heterogeneity of specific ventilation, and consequently of alveolar ventilation, will broaden LogSDQ̇. This may in part explain why MRI tended to overestimate LogSDQ̇ relative to MIGET.

Lastly, MIGET measures of LogSDV̇ are inherently more variable than those derived from LogSDQ̇. In our data, the correlation between paired measurements of LogSDQ̇ averaged 0.93, whereas for LogSDV̇ it was 0.81. We obtained two sets of duplicate inert gas measurements and averaged the results to minimize the contributions of random experimental error to our findings. However, this may have had some small effect on our findings especially given the number of subjects studied, where experimental noise may affect one subject more than another subject and affect the slope of the relationship.

Assumptions and Limitations Associated With MRI Quantification of Regional V̇_A/Q̇ Ratio

Measurement of alveolar ventilation.

Specific ventilation (32) measures the ratio of the delivery of fresh gas to resident gas and uses the lung proton density images to estimate the amount of resident gas. The assumption made is that proton density is a valid measure of all non-gas components such as plasma, alveolar fluid, blood and other intra/extra-cellular water. However there is a small non-water component that does not show up in the magnetic resonance signal (less than 10% of the water fraction) (23). We have previously estimated (17) that this may induce an error of measurement of 3–5% of ventilation.

While specific ventilation imaging does not depend on the magnitude of the signal change produced as the inspired Po₂ changes, the technique is subject to several assumptions. These include the assumption of uniformity of Po₂ in a voxel at end expiration, that the rate of equilibration of Po₂ between alveoli and lung water (thus changing the local MR signal properties) occurs much faster than one breath and a single ventilatory unit with a unique specific ventilation corresponds to a voxel. These assumptions are likely justified based on theory (10, 12, 28) and are also supported by validation studies of the SVI technique (31).

Use of hyperoxia to measure specific ventilation.

A potential confounding issue is that specific ventilation imaging uses oxygen as a contrast agent, which could affect blood flow in regions of the lung affected by hypoxic pulmonary vasoconstriction. The duration of the exposure is short, and for this reason we expect the effect, if any, to be small (27). Nonetheless for this reason, perfusion was measured during the air breathing portions of the experiment only.

Measurement of perfusion and elimination of large vessels.

In an ideal experiment one would tag the blood at some proximal location and image it on arrival in the distal capillary bed. However, in conducting an ASL experiment in the lung, the short T2* combined with the relatively long distances that blood has to travel to the capillary bed means that this is not possible because all of the signal would have decayed away by the time it was imaged. For this reason the ASL technique that we use in the lung has a tag location that encompasses the imaging plane. This presents some challenges in quantifying perfusion and the images contain large blood vessels that do not represent perfusion for three reasons. First, some are completely full of tagged blood and thus reflect blood volume rather than blood flow (7). Second, the blood contained in these large vessels may be destined for a distal capillary bed, not located in the slice of interest. Finally, these larger vessels may be on either the arterial or the venous side of the circulation. Another problem for quantifying regional V̇_A/Q̇ ratio is that a voxel entirely contained within a large vessel would be identified as a region of shunt (i.e., perfused but not ventilated), but this is incorrect, because large vessels are part of the “plumbing” and not of the gas-exchanging portion of the lung. For all of these reasons, these large vessels must be eliminated from the images before incorporation into the final V̇_A/Q̇ quantification.

Modeling work has shown that implementing a threshold corresponding to 35% of maximum blood delivered in ml/min/ml ensures that the contribution of perfusion to the total ASL signal is at least 80% (6). We have previously implemented this by identifying voxels containing the top 1% of signal, and retaining all voxels with perfusion below 35% of this value. While appropriate in noise-free model data, this approach may be problematic in the presence of experimental error, because it relies on a small amount of information to define the threshold and thus may be skewed by a very small number of voxels with extremely high signal. For this reason we implemented a recent technique (39) based on statistical spatial clustering. Large vessel maps are created based not on the ASL difference image, but on the 2-dimensional histogram of ‘tagged’ and ‘control’ images, and two classes are separated using a bivariate mix-model (39) identifying two sub-distributions corresponding to perfusion and large vessels. This technique does not depend on an operator set threshold, and is less sensitive to noise as it bases separation not on 1% of the data, but on the entirety of the data.

Registration effects of smoothing of images.

In order to quantify regional V̇_A/Q̇ ratios the images obtained during the SVI acquisition must be registered to allow for inconsistencies in breathhold volume and then registered to density images to provide regional alveolar ventilation. Finally, the ventilation images must be registered with perfusion images to provide the final V̇_A/Q̇ image. To minimize the effect of small errors in registration, the final V̇_A/Q̇ image is smoothed to ~1 cm³. The extent of smoothing is critical for comparison against MIGET, as too little smoothing may lead to errors and act to increase the measured heterogeneity in the MRI images. Conversely too much smoothing reduces the ability of the MRI technique to discriminate small regions of altered V̇_A/Q̇ ratio and is expected to reduce the heterogeneity and the values of LogSDV̇ and LogSDQ̇. The choice to smooth in-plane to ~5 voxels (~8 mm) resolution was driven by the need to minimize the inevitable small misalignment across techniques, multiple-end expiration imaging, and the range of validity of the registration technique.

Single slice image acquisition.

We imaged a single slice because the current acquisition time for the specific ventilation measurement is ~18 min for each slice imaged. We imaged in the sagittal plane, thus capturing gravitational effects in the lung, and with the maximal anterior-posterior dimension to maximize the amount of lung sampled. The image represented ~8% of the lung. In healthy subjects it is reasonable to expect that the lung is relatively uniform. However, in patients with focal lung disease it is probable that the entire lung will need to be measured to adequately capture the V̇_A/Q̇ distribution, although this has not been established.

Measurement of dead space and shunt.

We are unable to quantify either dead space or shunt with our MRI technique. Specific ventilation imaging measures the rate of change in the MRI signal intensity following a change in the $\mathrm{F}{\mathrm{I}}_{{\mathrm{O}}_{\mathrm{2}}}$ (32). In very well ventilated lung regions (specific ventilation >1) the equilibration is so rapid that it takes place within a single breath. Thus all specific ventilation values above that threshold are binned together, and this limits sensitivity to high V̇_A/Q̇ regions. Very rapidly equilibrating regions that show perfect correlation with the driving function and thus are consistent with dead space, but which are not separable from high specific ventilation regions, are eliminated from the analysis.

The limited ability to resolve high V̇_A/Q̇ ratios and deadspace may be of limited importance in most individuals because high V̇_A/Q̇ regions and deadspace represent “wasted” ventilation- they have minimal effect on oxygenation. However, regions of the lung corresponding to low V̇_A/Q̇ ratios or shunt are of much more importance for gas exchange. Voxels that do not show any correlation with the driving function in SVI imaging are also eliminated (specific ventilation < 0.05). These voxels may have poor signal intensity for several reasons: the voxels are entirely within large blood vessels, they have low signal to noise ratio, or they represent unventilated regions. Large vessels are eliminated from the analysis as previously described, but at this stage we cannot distinguish between voxels that are high in noise or voxels that are unventilated. For this reason, we do not have the ability to resolve shunt.

In conclusion, using a new proton MRI technique to measure regional V̇_A/Q̇ ratio we have found good to excellent relationships between measures of heterogeneity derived from MIGET and those derived from MRI. Although limited to a single slice acquisition, these data suggest that single slice measures of V̇_A/Q̇ ratio provides an adequate means to assess the normal lung.

GRANTS

This work was supported by the National Space Biomedical Research Institute through NASA NCC 9-58, and by National Heart, Lung, and Blood Institute Grants K99/R00 HL-093064, R01 HL-104118, R01 HL-119263, R21 HL-118539, and R21 HL-122753.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

R.C.S., A.C.H., P.D.W., G.K.P., and S.R.H. conceived and designed research; R.C.S., A.C.H., T.S.S., T.J.A., H.W., R.J.T., P.D.W., and S.R.H. performed experiments; R.C.S., A.C.H., T.J.A., H.W., R.J.T., P.D.W., and S.R.H. analyzed data; R.C.S., A.C.H., P.D.W., G.K.P., and S.R.H. interpreted results of experiments; R.C.S., A.C.H., and S.R.H. prepared figures; R.C.S., A.C.H., and S.R.H. drafted manuscript; R.C.S., A.C.H., T.S.S., T.J.A., H.W., R.J.T., P.D.W., G.K.P., and S.R.H. edited and revised manuscript; R.C.S., A.C.H., T.S.S., T.J.A., H.W., R.J.T., P.D.W., G.K.P., and S.R.H. approved final version of manuscript.