Fig. 8.
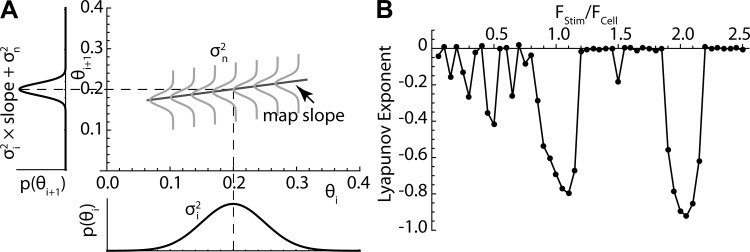
Slope of the iterative map determines accumulation of error. A: at phase lock in the presence of noise, the phase of the ith spike is described as a probability distribution with variance σi2. During the interspike interval, exposure to noise introduces additional variability with variance σn2. If the slope of the map is larger than zero, some of the variance of the ith interspike interval will propagate to the next, and errors will accumulate. The rate of accumulation is equal to the slope of the map. B: the Lyapunov exponent is the mean value of log of the slopes of all visited points on the map. It predicts the frequencies at which errors will accumulate, with a value of zero meaning summation of errors over time and with negative values associated with small values of slope and frequencies at which error accumulation will be minimal. Note the similarity between the graph in B and the mean errors shown in Fig. 7.