Mechanical strain-sensing implicated in cell shape recovery in Escherichia coli

Abstract

The shapes of most bacteria are imparted by the structures of their peptidoglycan cell walls, which are determined by many dynamic processes that can be described on various length-scales ranging from short-range glycan insertions to cellular-scale elasticity.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} Understanding the mechanisms that maintain stable, rod-like morphologies in certain bacteria has proved to be challenging due to an incomplete understanding of the feedback between growth and the elastic and geometric properties of the cell wall.^{3, 4, 12, 13, 14} Here we probe the effects of mechanical strain on cell shape by modeling the mechanical strains caused by bending and differential growth of the cell wall. We show that the spatial coupling of growth to regions of high mechanical strain can explain the plastic response of cells to bending⁴ and quantitatively predict the rate at which bent cells straighten. By growing filamentous E. coli cells in donut-shaped microchambers, we find that the cells recovered their straight, native rod-shaped morphologies when released from captivity at a rate consistent with the theoretical prediction. We then measure the localization of MreB, an actin homolog crucial to cell wall synthesis, inside confinement and during the straightening process and find that it cannot explain the plastic response to bending or the observed straightening rate. Our results implicate mechanical strain-sensing, implemented by components of the elongasome yet to be fully characterized, as an important component of robust shape regulation in E. coli.

Cell shape, which in many types of bacteria is determined by a mechanically rigid peptidoglycan (PG) cell wall, is crucial for bacterial motility, proliferation, adhesion, and survival.^{1, 2, 3} Rod-like bacteria maintain their shapes at a fixed diameter with extraordinary precision during growth and elongate by the action of the peptidoglycan elongation machinery (PGEM), a multi-enzyme complex consisting of penicillin binding proteins (PBPs) and conserved membrane proteins (MreC, MreD, RodA, RodZ, and other shape, elongation, division, sporulation (SEDS)-family proteins).^{5, 6, 15, 16} Recent experimental studies have led to a qualitative description of cell wall growth on a molecular level: the PGEM interacts with the actin homolog MreB to direct the local, circumferential insertion of new glycan strands into the existing PG structure. Although the general roles of PGEM enzymes in cell wall elongation are well-studied,^{5, 6, 7, 8, 9, 17} the feedback mechanism between cell shape—as determined by the geometric and elastic properties of the cell wall—and PGEM-related subcellular components is not understood. It is unclear whether the mechanisms needed to maintain robust cellular morphology detect cellular geometry^{12, 18} or mechanical stresses.^{3, 4, 13, 14}

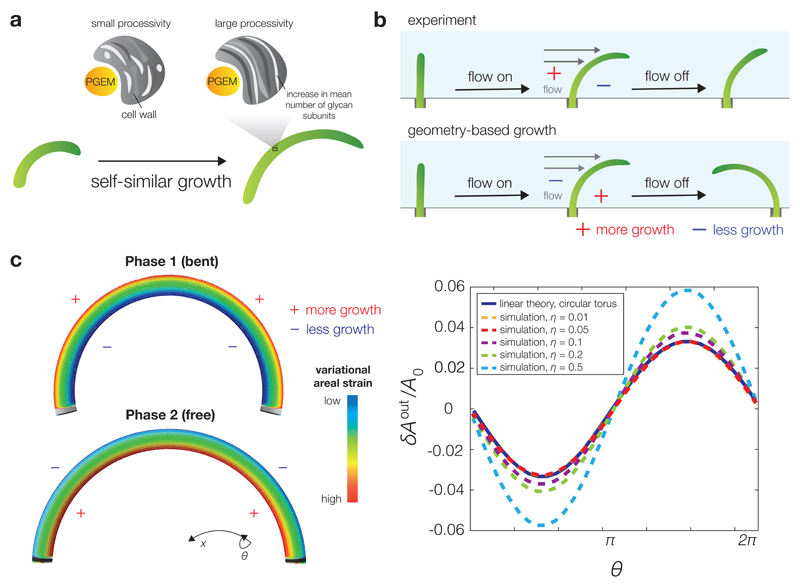
Recent progress has been made toward understanding the regulatory mechanisms controlling rod-like cell shape by mechanically perturbing PG, which can be modeled as a partially ordered elastic sheet subject to both plastic and elastic deformations.^{3, 4, 14, 19} E. coli cells adapt their growing morphologies to confining environments^{20, 21} or applied hydrodynamic drag forces^{4, 19} by elongating in a manner which results in bending. In several experiments, E. coli cells recovered their straight, native rod-like morphologies upon release from confining environments^{4, 19, 20, 21} or disruption of an induced crescentin structure²² after sufficient growth. This striking robustness has led to three prevalent theories of shape regulation: (1) a large processivity—the mean number of subunits incorporated into a glycan strand from initiation to termination of the elongation step—provides a built-in mechanism for straightening;²³ (2) PGEM-related molecules such as MreB localize, according to cell wall geometry, to regions of negative Gaussian curvature;^{12, 18} and (3) new glycan strands are preferentially inserted at regions of high mechanical stress in a manner that straightens the cell.^{4, 13, 22, 23}

By itself, the processivity of PG synthesis cannot explain cell straightening. Although processive glycan insertions into the PG mesh have been shown to yield an exponential decay of curvature,²³ an exponential increase in length due to growth counteracts the straightening and leads to a self-similar, scale-invariant shape even in the limit of infinite processivity.^{3, 24} The local curvature of a growing, self-similar crescent-shaped cell decays, but in the absence of cell division the cell is always bent and not truly rod-like (Fig. 1a). Similarly, the possible curvature-sensing abilities of PGEM-related subcellular components have been interpreted as a geometry-based feedback mechanism for shape regulation.^{12, 18} Such mechanisms would allow the cell to preferentially grow at regions of negative Gaussian curvature and thus result in straightening. However, such a mechanism cannot explain experiments subjecting E. coli and Bacillus subtilis cells to hydrodynamic drag.^{4, 19} If the local growth of PG were biased towards regions of negative Gaussian curvature, then more growth would occur along the edge facing away from the flow. Upon extinguishing the flow, the cells would bend in the direction opposite the flow because of the stored, anisotropic growth (Fig. 1b). It was observed, on the contrary, that the equilibrated, bent conformations were in the same direction of the flow.

Figure 1. Three theories for cellular shape regulation.

a, The processivity of glycan insertions provides a robust, built-in mechanism for curvature decay, but even in the infinitely processive limit a cell remains self-similar. b, A geometry-dependent growth mechanism predicts an oppositely-bent shape once an applied hydrodynamic drag force is extinguished, which was not observed in previous experiments. c, A mechanical strain-dependent growth rate can explain both the elastic snapback shown in b and straightening, and the straightening rate can be quantitatively predicted. (Left) Simulated equilibrium configurations of a bent cylinder (top) and a toroidal shell (bottom) subject to an internal pressure, which respectively describe the cell states under a bending force (Phase 1) and in the absence of a bending force (Phase 2). The mesh, processed using finite-element software, is colored by the variational areal strain δA. Like the differential growth, δA flips signs between the two phases. (Right) The simulated, normalized variational areal strain for c = 0.1 and varying values of dimensionless pressure η are plotted against the azimuthal angle θ, along with the linear theory prediction, for a Phase 2 cell. Values of η are calculated using the radii of deformed states. The Poisson ratio is taken to be ν = 0.3 and the remaining simulation parameters are detailed in the Supplementary Methods.

We therefore hypothesized that a mechanical strain-based, as opposed to geometry-based, pattern of preferential PG elongation could reconcile the aforementioned observations and robustly straighten a cell. The elastic quantity that we examine is the areal strain, which measures the local stretching of PG and is defined in terms of the axial and circumferential components of the strain tensor u_xx and u_yy, respectively, as A = (1 + u_xx)(1 + u_yy) − 1. A molecular mechanism which couples growth to PG pore size, for instance, may sense areal strain. As we discuss below, the key assumptions of our model are that (1) the elastic properties of the cell wall are unaltered by growth; and (2) the number of glycan strand initiations per unit area is modulated by areal strain. With these assumptions, we will show that strain-dependent PG elongation is quantitatively consistent with both the earlier flow-based experiments⁴ and novel experimental measurements of the straightening rate.

To test our hypothesis of strain-dependent PG elongation, we designed an experiment consisting of two phases: in Phase 1, filamentous cells are confined and uniformly bent in curved microchambers. In Phase 2, the cells are released from captivity and their straightening rates are measured. Before reporting our experimental results, we discuss the theoretical predictions of our model.

As discussed in detail in the Methods, using linear elasticity theory we determined the areal strain experienced by the cell wall at an angle θ and time t in both Phases 1 (“in”) and 2 (“out”) as

$$A^{\text{in}}(\theta ,t)\approx A_0+A_1^{\text{in}}(B_0-c_0)\text{sin}\theta ,A^{\text{out}}(\theta ,t)\approx A_0-A_1^{\text{out}}c(t)\text{sin}\theta ,$$ (1)

where A₀ is a constant, B₀ is the ratio of the cell radius, r, to the radius of curvature of a bent cell in Phase 1, which is assumed small compared to unity and partially relieved by a smaller, constant differential growth parameter c₀ < B₀, and both $A_1^{\text{in}}=1+\eta -\nu -\eta \nu +\eta {\nu }^2$ and $A_1^{\text{out}}=\frac{\eta }{4}(2+\eta -2\nu -4\eta \nu +\eta {\nu }^2)$ are positive for the parameter values relevant to E. coli (Supplementary Table 1). Here η = pr/Y is a dimensionless pressure, p is the turgor pressure, Y and ν are respectively the two-dimensional elastic modulus and Poisson ratio of the cell wall, and θ = π/2 and θ = −π/2 specify respectively the outer and inner edges of the cell. The differential growth parameter is defined so that the arclengths of the inner and outer edges differ by 2c₀L, where L is the length along the cellular midline, and the assertion that c₀ < B₀ is consistent with an elastic snapback wherein removing the bending force results in a sudden decline of curvature from B₀/r to c₀/r. The variational component $\delta A^{\text{out}}=-A_1^{\text{out}}c(t)\text{sin}\theta$ is opposite in sign to $\delta A^{\text{in}}=A_1^{\text{in}}(B_0-c_0)\text{sin}\theta$ and expressed as a function of a time-dependent differential growth parameter c(t). Importantly, the variational components in both Phases 1 and 2 agree in sign with the differential growth profiles (Fig. 1c).

Given the variational areal strains, we modeled areal strain-dependent growth by assuming that the number of glycan strand initiations γ per unit area can be decomposed into strain-independent and strain-dependent components:

$$\gamma (\theta ,t)=k+\alpha \delta A(\theta ,t),$$ (2)

where k is a constant, strain-independent rate, δA(θ, t) is the variational areal strain as a function of angle θ and time t, and the parameter α quantifies the intensity of growth-strain coupling. The average initiation rate k can be determined by factors other than strain and need not depend on mechanical stress or turgor pressure.²⁵ For instance, a growth mechanism may depend only on the abundance of PGEM constitutents in maintaining an average initiation rate over the entire cell, but be biased towards regions of high strain in a manner that does not increase the average initiation rate.

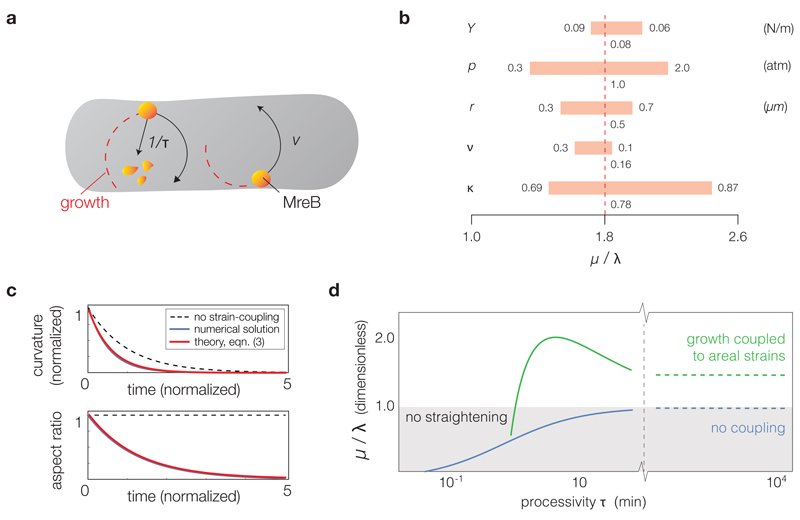
To quantify the straightening rate arising from areal strain-dependent growth, we coarse-grained E. coli’s growth dynamics by first assuming MreB filaments, which are spatially correlated with new glycan insertions,²⁶ to correspond to PG growth sites. This is consistent with a growth scheme in which MreB filaments orchestrate persistent motion of the PGEM, but differential glycan strand initiation depends on strain-sensitive elongasome components. Although MreB filaments have been observed to move at a helical pitch angle,²⁶ the small pitch allows us to model them as point molecules moving circumferentially along the inner membrane with a spot velocity of v = 5 nm/s, corresponding to experimentally observed values^{27, 28, 29} (Fig. 2a). We further modeled the decay of an MreB filament as a Poisson process with rate 1/τ, where τ ≈ 5 min is the spatial persistence time of membrane-bound MreB,¹² a value that is consistent with our snapback measurements (Supplementary Discussion). Convolving γ with the width of PG inserted per growth site then yields an integro-differential growth equation describing the pole-to-pole cell length L(θ, t) at any angle θ and time t (see Supplementary Note 2 for a derivation and solution of this equation). As the pole-to-pole lengths determine the midline curvature C(t) at any point in time, solving the growth equation results in a theoretical prediction of the straightening rate. In the limit of large processivity, we found an approximate relation between the normalized straightening rate µ = −dC/(Cdt), the normalized growth rate λ = dL/(Ldt), and the snapback ratio κ = c₀/B₀ as

$$\mu \approx \lambda \left(1+\frac{\kappa A_1^{\text{out}}}{(1-\kappa )A_1^{\text{in}}}\right).$$ (3)

Figs. 2b-c illustrate the prediction of equation (3), which varies depending on processivity (Fig. 2d), for the parameter values of E. coli summarized in Supplementary Table 1 and a snapback ratio obtained from the experiments described below.

Figure 2. Areal strain-dependent PG elongation quantitatively predicts shape recovery dynamics.

a, MreB molecules are modeled as points that move circumferentially along the PG mesh with a spot velocity v and unbind as a Poisson process with rate 1/τ. The growth at an angle θ at a given time depends on the number of initiated glycan strands also at θ, which in turn depends on the strain profile of the cell in the past (see also the growth equation in Supplementary Note 2). b, A sensitivity analysis of the theoretically predicted straightening rate for several material properties, assuming a large MreB processivity of M τ = 6 radians. The elastic snapback and material parameters determine the value of the areal strain-coupling parameter α self-consistently, as discussed in Supplementary Note 2. The predicted straightening rate is consistent with the experimental data shown in Fig. 3c. c, Numerical solutions of the growth equation agree with the theoretical prediction for the straightening rate. Here the aspect ratio is defined as the product of arclength and curvature, L(t)C(t), which does not decay without areal strain-coupling in the limit of infinite processivity (dashed lines; see also Supplementary Video 11). The normalized time is defined with units of 1/λ = t_d/ ln(2). d, There is an intermediate value of the processivity, measured in units of time for a constant rate of PG subunit insertion, for which mechanical strain-sensing confers the largest effect on straightening. Empirical values of MreB processivity, intriguingly, lie close to the optimal value at which a cell straightens fastest.

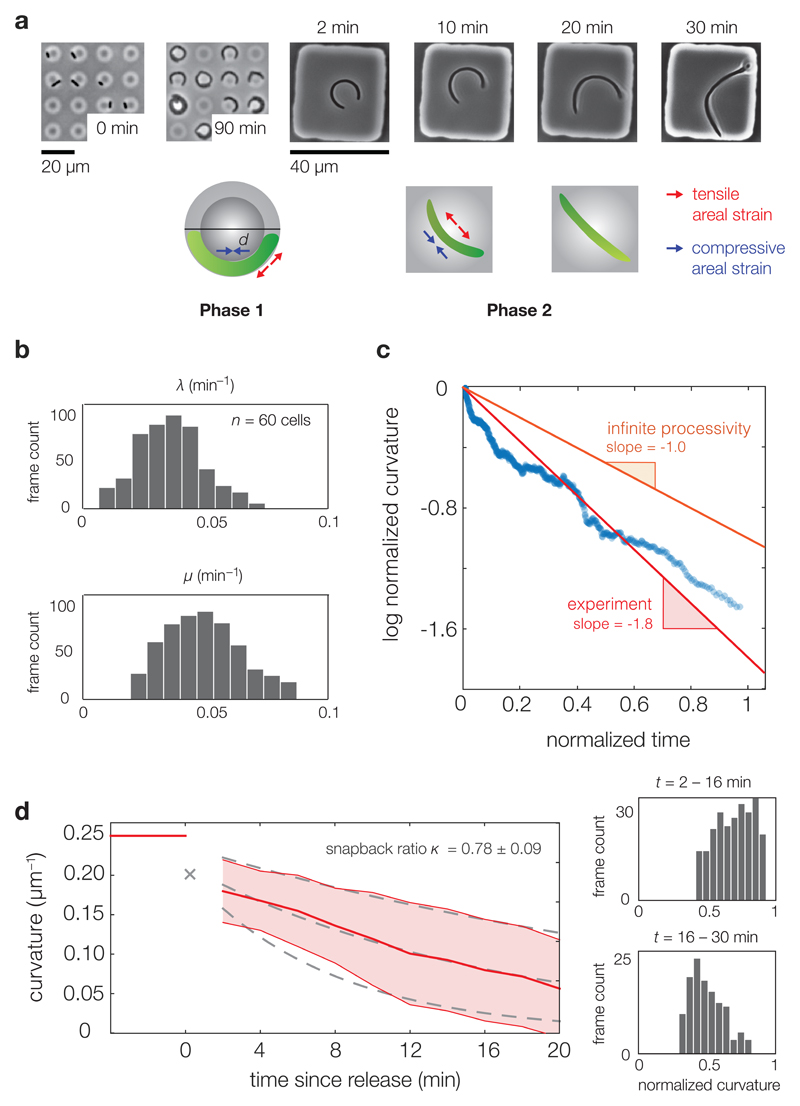
While previous studies examined the plastic deformation of E. coli cells under flow,^{4, 19} these experiments were limited to several cells and the areal strains were nonuniform in the axial directions of the cells. To test our theory of strain-dependent growth, we therefore conducted experiments following the two phases described above. In Phase 1, filamentous E. coli cells grew in toroidal microchambers with constant diameters of d = 8 µm (Fig. 3a). The cells were confined to the microchambers during growth and extracted into a larger, square-shaped microchamber once they filled over 90% of the microchamber circumference. Elastic snapbacks of the cells were observed after extraction, in agreement with flow-based experiments⁴ (Supplementary Discussion). In Phase 2, we imaged the shape recovery process of unconfined cells in two minute intervals for over 40 minutes (Supplementary Videos 1-10).

Figure 3. Quantitative analysis of cellular straightening dynamics.

a, In our experiments, filamentous E. coli cells were grown in confined, toroidal microchambers of diameter d = 8 μm. An elastic snapback was observed upon removal, after which the cells recovered their straight, rod-like morphologies over time. Images shown correspond to before (0 min and 90 min) and after (2 min, 10 min, 20 min, and 30 min) microchamber release. b, Histograms for the instantaneous growth rate λ = dL/(Ldt) and instantaneous straightening rate μ = −dC/(Cdt) for 60 E. coli cells. c, A plot of the log normalized curvature, defined as ln(C(t)/C(2 min)), as a function of time since release (in units of t_d/ ln(2)) for all 60 cells in Phase 2. A 50-point moving average filter along the temporal direction was applied to smooth out the data. The population-averaged straightening-to-growth ratio is 〈μ〉/〈λ〉 = 1.8, which cannot be explained by an infinite processivity of PG synthesis. The slower rate of decrease of the log normalized curvature for large times may be an artifact of substrate pinning for large cells. d, (Left) Extrapolating the population-averaged curvature to the time of microchamber release at t = 0 yields a mean elastic snapback ratio of κ = 0.78 ± 0.09. Shaded areas denote values within one standard deviation of the population mean. The gray dashed lines denote exponential fits to values which are one standard deviation away from the population average. (Right) The distributions of aggregated normalized curvatures C(t)/C(0) at times t = 2–16 min and t = 16–30 min.

Upon imaging the recovery process, we quantitatively analyzed the straightening dynamics of unconfined Phase 2 cells (the methodology and results are detailed in the Supplementary Methods and Supplementary Fig. 7). We extracted the normalized growth rate λ from the arclengths of the resulting fits for 60 cells and found a population-averaged value of 〈λ〉 = 0.021 min⁻¹ (Figs. 3b-c and Supplementary Fig. 8). This value of 〈λ〉 reflects a doubling time of t_d = 33 min, in agreement with bulk culture growth measurements.^{30, 31} Similarly, we extracted the normalized straightening rate µ from the curvatures of the fits and found a population-averaged value of 〈µ〉 = 0.038 min⁻¹, 1.8 times larger than the growth rate. Extrapolating the population-averaged curvature to the time of release, two minutes before the first frame, yields a mean elastic snapback ratio of κ = 78%, with an extrapolated standard deviation of 9% (Fig. 3d). The observed straightening rate and snapback ratio are consistent with equation (3) (Figs. 2b-c) and numerical simulations of the growth process (Supplementary Figs. 5-6 and Supplementary Video 11) for the material values of E. coli summarized in Supplementary Table 1.

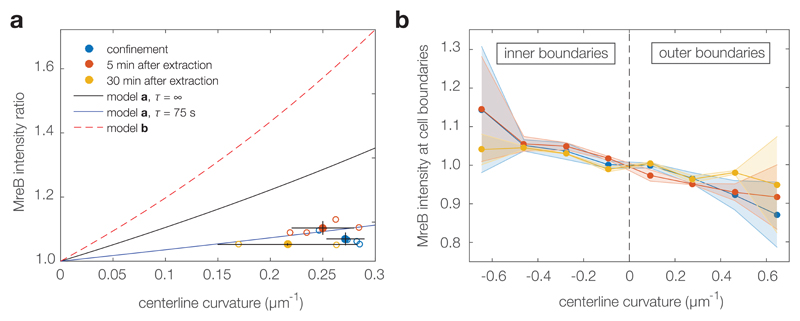
We next wondered whether MreB—which is believed to localize to regions of negative Gaussian curvature in cells with submicron-scale indentations¹²—-could also sense strain or otherwise account for straightening by localizing to the inner edge in unconfined Phase 2 cells. To test the possibility that MreB localization could explain cell straightening, we repeated the foregoing experiments with a fully functional and complementing MreB-msfGFP fusion expressed from the native mreB locus.³² We measured MreB fluorescence intensities at the inner and outer edges of both Phase 1 and 2 cells using an approach similar to previous work¹² (see Supplementary Methods and Supplementary Figs. 9-10 for details). In qualitative agreement with previous work,¹² we found increased MreB-msfGFP intensities at the inner edges of confined Phase 1 cells (Fig. 4a), with an enrichment positively correlated with the centerline curvature (Fig. 4b), indicating that MreB localization alone cannot account for growth inside confinement in Phase 1. We also found an increased MreB-msfGFP intensity at the inner edges of recovering Phase 2 cells. However, the MreB enrichment is not sufficient to explain a straightening ratio of 1.8 based on a model in which cell elongation is proportional to MreB density (Fig. 4a). Together, these results indicate that MreB localization cannot explain differential growth in both Phases 1 and 2. Furthermore, while we do not rule out an active mechanism for curvature-sensing in submicron-scale indentations, the observed MreB localization between the inner and outer edges of bent cells does not require an active sensing mechanism but can be explained by constant initiation and persistent circumferential motion alone (Fig. 4a).

Figure 4. MreB-msfGFP fusion cells exhibit MreB enrichment at negative Gaussian curvature, but MreB enrichment alone cannot explain straightening.

a, MreB is predominantly localized at the inner edges of filamentous MreB-msfGFP E. coli cells. Shown is the MreB-msfGFP intensity ratio between the inner and outer cell edges, measured in confinement, after release from confinement, and 30 minutes into recovery. For each condition, open circles indicate averages obtained from at least 15 cells per replicate experiment, as detailed in the Methods section. Filled circles indicated averages over replicates and error bars indicate standard deviations between replicates. The solid curves indicate the predicted MreB intensity ratio for a model of constant MreB initiation rate and different processivity times τ, assuming a spot velocity of v = 5 nm/s (model a in the legend; for details, see Supplementary Note 2). The dashed line indicates the MreB intensity ratio that would be required to account for the observed straightening ratio of 1.8 within a model where cell-wall synthesis depends only on MreB localization (model b in the legend). Thus, MreB localization is consistent with a model of constant initiation and finite processivity, and the observed intensity ratio is not sufficient to account for cell straightening. b, The MreB-msfGFP intensities decrease as a function of signed centerline curvature where the inner and outer edges of a cell correspond to negative and positive values of centerline curvature, respectively. Error bars denote standard deviations, as in a.

The consistency of our strain-based model with experimental results suggests that mechanical strains arising from differential growth can act as a sensory cue for robust shape regulation. Subsequent simulations and stress analyses indicate that other sources of variation in elastic quantities, particularly nonuniform crosslinking of glycan strands or cleavage of peptide bonds, cannot explain the observed straightening rate (Supplementary Note 1 and Supplementary Figs. 3 and 4). However, while our results constrain models which can explain straightening, further work will be needed to experimentally demonstrate that mechanical strain mediates PG elongation and uncover the molecular mechanisms responsible for mechanical strain-sensing. One intriguing possibility for such a mechanism is the lipoprotein-PBP interaction, which may be sensitive to PG pore size.^{9, 33, 34, 35} We anticipate future experiments to determine possible effects of the lipoprotein-PBP interaction and other perturbations, such as osmotic shock (Supplementary Discussion and Supplementary Fig. 11), on straightening.

In summary, we have used a combination of theory and experiment to quantitatively reveal and explain shape recovery in cells that have been released after growing in a confined environment. Our findings underscore how perturbing cells using physical, in contrast to biological, approaches can uncover how cells function in their native conformations. Because cell wall strains are determined by the entire deformation history of the cell, strain-sensitive growth can enable the robust recovery of native rod shape,^{3, 4, 13, 14} in addition to allowing cells to adapt to growth in various geometries by relieving cell wall stresses and regulating cell wall thickness by localizing growth to thinner regions of PG, where the areal strains are larger. By showing that coupling growth to mechanical strain can quantitatively explain shape recovery, our analysis contributes to our understanding of the possible biophysical mechanisms that underlie the remarkable diversity and robustness of cellular morphology.

Methods

Areal strain profiles of a cell in Phases 1 and 2

To quantify the areal strain incurred by a bent, filamentous cell due to nonuniform growth, we modeled the bacterial cell wall as a homogeneous, isotropic, linear-elastic shell under pressure. For the spatial coupling of growth to regions of high areal strain to be consistent with the elastic snapback observed in previous flow-based experiments (Fig. 1b), it is necessary that a bending force makes the areal strain larger on the outer edge of the cell. It is also necessary that the residual stresses caused by turgor pressure and anisotropic growth during bending make the areal strain smaller on the outer edge once the bending force is removed. A mechanical strain-dependent growth rate, in which the initiation rate of new glycan strands quantitatively depends on the areal strain, would then explain the ability of the cell to both plastically adapt to a bending force and straighten in the absence of external forces.

When a cell is bent uniformly by an external force (Phase 1), the areal strain, which is sinusoidally varying in the azimuthal coordinate θ and constant in the axial direction, is readily determined by elasticity theory and is larger on the outer edge due to the axial stresses incurred by bending (Supplementary Note 1 and Supplementary Fig. 1). Determining the areal strain once the bending force is removed (Phase 2) requires consideration of growth as the cell is bent. It is convenient to model growth by changing the intrinsic geometry of the cell, which is the shape a cell would assume in the absence of external forces such as pressure.^{36, 37} Any growth in the axial direction that couples to a sinusoidally varying areal strain profile is also sinusoidally varying, so the intrinsic pole-to-pole PG length becomes larger at the outer edge and smaller at the inner edge in Phase 1 (Fig. 1c). As a result of this differential growth, the intrinsic geometry of the cell evolves from that of a cylinder to that of a torus, a geometry for which the pole-to-pole lengths are sinusoidally varying. The toroidal geometry is described by the cell radius r and a differential growth parameter c, which quantifies the cellular growth asymmetry.

Assuming that growth does not change the elastic properties of a cell, the areal strain of a Phase 2 cell can be determined. Although the shape of a circular torus would exactly realize the intrinsic geometry resulting from differential growth, the presence of a turgor pressure can result in a different geometry and stress state. We therefore undertook finite-element stress analyses of a closed, circular toroidal shell section subject to internal pressure (see Supplementary Methods for a detailed discussion of the simulation methodology and results). We found that, for both infinitesimal and moderate strains, the stress profiles were well-approximated by the linear theory result in which the deformed geometry remains that of a circular torus (Fig. 1c and Supplementary Fig. 2), with a circumferential stress component that is larger on the inner edge. Interestingly, the sources of the variational terms δAⁱⁿ and δA^out are the axial and circumferential components of the stress tensor, respectively, and neither one of the variational stress components alone flips signs between Phases 1 and 2 (Supplementary Note 1).

Equilibrium simulations of an elastic shell

Stress analyses of closed cylindrical and toroidal shells subject to internal pressure were computationally undertaken with finite-element simulations using Abaqus FEA (Dassault Systems, Providence, RI). Explicit details of these simulations are discussed in the Supplementary Methods. Abaqus input files were created with MATLAB, with shells being discretized uniformly into approximately 10,000 S4R elements, assigned material properties faithful to that of the E. coli cell wall, and equilibrated with respect to a range of internal pressures and material parameters. The axial and circumferential stress resultants were then extracted from the deformed state and used to compute the areal strain.

Numerical solutions of the growth equation

Numerical solutions of the growth equation were found in MATLAB by discretizing the integral as a Riemann sum and subjecting two time series, one for each of the lengths of the inner and outer edges of the cell, to the specified difference equation. The curvature along the midline is obtained as $C(t)=\frac{L(\pi /2,t)-L(-\pi /2,t)}{r(L(\pi /2,t)+L(-\pi /2,t))},$ where L(θ, t) is the pole-to-pole length at angle θ and time t and r is the cell radius. Discrete simulations of the growth process were also undertaken, as discussed in the Supplementary Methods, and are summarized in Supplementary Fig. 5 and Supplementary Video 11.

Microfabrication

We designed patterns of microchambers in donut-shaped designs in CleWin (Delta Mask, The Netherlands) and square-shaped designs in Adobe Illustrator (Adobe Systems, San Jose, CA). The design of the donut-shaped microchambers was inspired by previous work.²⁰ We made designs of donuts with outer diameters of 8 µm (channel width 2 µm), corresponding to circumferences of approximately 25 µm (Fig. 2a). The number of donut-shaped microchambers is about 40,000 per array. The microfabrication process has been reviewed in detail³⁸ and previously described for microchannels and microchambers.^{18, 39} Pristine silicon dioxide wafers were cleaned in isopropanol and ddH₂O repeatedly. For donut-shaped microchambers, we used positive photoresist Shipley 1813 (MicroChem, Newton, MA). Prior to spincoating, a vapour of hexamethyldisilazane (HDMS) is deposited on the clean silicon dioxide wafer substrate to prime for adhesion of the photoresist. The spincoating results in approximately 1.3 µm thick layers of photoresist. For square-shaped microchambers, we used negative photoresist SU8-3010 (MicroChem, Newton, MA) directly spincoated onto clean silicon dioxide wafers to produce approximately 20 µm thick polymer layers. Layer thicknesses were confirmed using a surface profilometer (Tencor AlphaStep 200, Milpitas, CA). Donutshaped microchambers were directly written onto the photoresists via laser lithography (µPG 101, Heidelberg Instruments, Heidelberg, Germany). Photomasks (CAD/Art Services, Inc., Bandon, OR) were used for the transfer of square-shaped microchambers onto the photoresist using UV-lithography. The patterns were developed with MF-321 and SU-8 developer (MicroChem, Newton, MA), respectively. We silanized the resulting photoresist master overnight using a vapour of (tridecafluoro-1,1,2,2-tetrahydrooctyl)trichlorosilane (Gelest, Inc., Morrisville, PA). Applying soft lithography,⁴⁰ we transferred the pattern into polydimethylsiloxane (PDMS) (Sylgard 184, Dow Corning) using a ratio of 10:1 (base to curing agent), and cured the polymer overnight at 60°C. The resulting PDMS layer contained patterns of microchambers in bas-relief and was used as a stamp to emboss a layer of agarose or agar²⁰ for bacteria cell growth. We poured a hot solution (65°C) of 4% lysogeny broth (LB)-agarose (EM-2120, Omni-pur, EM Biosciences) containing IPTG and antibiotics (if required) on PDMS stamps oriented with the features facing up, and cooled them to room temperature to gel the agarose. We cut out the layer of LB-agarose embossed with microchambers using a scalpel and prepared the microchambers for growth experiments.

Bacterial strains and growth

We used E. coli MG1655 with plasmid encoding SulA (a cell division inhibitor^{41, 42}) under an inducible lac promoter to induce filamentation with 1mM isopropyl β-d-1-thiogalactopyranoside (IPTG, Sigma Aldrich, St Louis). Bacteria were grown in liquid LB^{43, 44} (LB: 10g/L tryptone, 5g/L yeast extract, 10g/L NaCl), and, if required, supplemented with appropriate antibiotics. LB media containing 1.5% Difco agar (w/v) was used to grow individual colonies. Tryptone, yeast extract, peptone, Petri dishes, and bacteriological agar were from Becton Dickinson (Sparks, MD) and sodium chloride was from Fisher Scientific (Fairlawn, NJ). We grew bacteria from a single colony in LB at 30°C overnight and supplemented the media with 100 µg/mL ampicillin (Sigma Alrich, St Louis) for plasmid selection. We used a 1:1,000 dilution to inoculate fresh liquid LB media. The culture was grown at 30°C with shaking at 200 rpm to an absorbance of approximately 0.6 (λ = 600 nm). At this point, we added IPTG to a final concentration of 1 mM and incubated the solution for another 5 minutes to initiate filamentation (expression of SulA) under shaking at 30°C. Subsequently, we added approximately 3-5 µL of the bacterial culture to the top of the donut-shaped microchambers (embossed in LB agarose with 1 mM IPTG, no antibiotics), incubated the agarose slab for 30 seconds, and sealed the microchambers with a #1.5 cover slip (12-548-5 g, Fisher Scientific). The microchambers were incubated in a static incubator at 30°C for at least 2 hours and the progress of filamentation was monitored every 20 minutes thereafter. Once the majority of cells were sufficiently filamented, we cut out the donut-shaped microchambers from the LB-agarose slab with a scalpel. We placed a 10 µL drop of LB-IPTG solution on a clean glass cover slip, used tweezers to hold the LB-agarose slab, and lifted the microchambers in and out of the drop to release the cells from the microchambers. We repeated this step at least 20 times. The remaining drop was pipetted carefully, added on top of the square-shaped microchambers, and sealed with a cover slip. We then immediately started imaging of the recovery process. Note that we also used E. coli MG1655 with the addition of 20 µg/mL cephalexin as we have done successfully before for spheroplast formation.³⁹ However, genetic manipulation generated less perturbations during the filamentation process, and we observed frequent cell lysis under antibiotic pressure even at low cephalexin concentrations.

The MreB-msfGFP strain used for MreB localization experiments carries a functional MreB-msfGFP translational sandwich fusion in the native mreB locus (MG1655, mreB′-msfGFP^SW-mreB′) previously described and characterized³² and the same pSulA plasmid described above to inhibit cell division. For MreB localization experiments, the MreB-msfGFP strain was grown overnight from a frozen stock at 37°C in LB plus ampicillin (100 µg/mL) in a shaking incubator. The overnight culture was washed and diluted 1:500 in M63 minimal media⁴⁵ containing glucose (0.4% wt/vol), NH₄ (20 mM), casamino acids (0.2% wt/vol), and ampicillin (100 µg/mL). M63 media was used during MreB localization experiments for enhanced fluorescence, while liquid LB, as described above, was used otherwise. The difference in media is not expected to affect our results, as elastic snapback measurements and MreB motion are robust over a range of growth conditions.^{4, 27} The culture was grown at either 37°C or 30°C as indicated to OD₆₀₀ ~ 0.1 in the shaker. Then, 1 mM IPTG was added to induce SulA expression, and cells were grown for approximately half a doubling time (~20 minutes at 37°C or ~40 minutes at 30°C) in the shaker before being harvested for microchamber confinement and microscopy. MreB-msfGFP intensity measurements were performed on cells grown in minimal media for reduced autofluorescence and at 37°C for increased growth rates. We confirmed that cells grown at 30°C behave quantitatively similar, in terms of their average curvature and MreB enrichment, during confinement and after release from the microchambers (Supplementary Table 2).

Microscopy

We used a Zeiss Axiovert 200 (Zeiss, Jena, Germany) inverted microscope with an enclosing custom-made incubation chamber (at 30 and 37°C) equipped with an Axiocam 503 mono CCD (Zeiss, Jena, Germany) and a 40x objective (EC Plan-neofluar, NA 0.75). The imaging was confined to square microchambers of length 40 µm. The time between each frame during timelapse measurements is 2 minutes. Images were recorded using AxioVision (v. 4.8, Zeiss, Germany). We used ImageJ (NIH, Bethesda, MD) for cropping raw timelapse images and exported the files as image sequences.

MreB-msfGFP cells were confined in toroidal microchambers of 8 µm outer diameter and 2 µm inner diameter, similar to the experiments described above (but with a smaller inner diameter). In contrast, the agarose microchambers used were made from M63 minimal media containing IPTG. To study MreB localization in confinement, cells were grown in microchambers for approximately two doubling times (~80 min at 37°C or ~160 min at 30°C) before imaging. At this time, cells had an average length of ~10 µm (Supplementary Table 2). Subsequently, cells were extracted in the same way as described above. Extracted cells were sandwiched between a flat 1% M63 agarose pad and a cover glass for cell immobilization and microscopy. During the time from cell extraction to imaging (~5 min), cells were maintained at room temperature to minimize elongation. To study MreB localization during recovery, extracted cells were incubated in M63 minimal media for the indicated time in PCR tubes at 37°C before being placed and imaged on M63 agarose pads in the same manner as immediately after extraction. MreB-msfGFP cells were imaged by phase-contrast and epifluorescence microscopy using an inverted microscope (TI-E, Nikon Inc., Melville, NY) equipped with a 100x phase contrast objective (CFI Plan Apo Lambda DM 100x 1.4NA, Nikon Inc., Melville, NY), a solid-state light source (Spectra X, Lumencor Inc., Beaverton, OR), a multiband dichroic (69002bs, Chroma Technology Corp., Bellows Falls, VT), and excitation (485/25) and emission (535/50) filters. Images were acquired using a sCMOS camera (Orca Flash 4.0, Hamamatsu, Japan) with an effective pixel size of 65 nm.

We acquired imaging data for 132 non-fusion cells over 24 replicate experiments, out of which 60 were analyzed (Fig. 3), and approximately 70 cells under osmotic shock over 6 replicate experiments, out of which 49 were analyzed (Supplementary Fig. 11). As discussed below, the cells which were analyzed were selected because their curvatures were quantified accurately by our image analysis. We performed 4 experiments with 34, 18, 48, and 19 MreB-msfGFP cells, 4 experiments with 33, 34, 30, and 35 MreB-msfGFP cells, and 2 experiments with 17 and 15 MreB-msfGFP cells for the confinement, 5 min after extraction, and 30 min after extraction cases, respectively, in Fig. 4.

Shape analysis

Cell identification, outlining, and skeleton detection for the length and curvature measurements was performed using a custom-made, MATLAB-based software package called CurvatureTracker, which is available upon request. We found pre-existing software, such as MicrobeTracker,⁴⁶ to not provide adequate tools for automating the collection of curvature data required in this work. CurvatureTracker uses Sobel edge detection, morphological opening, cluster analysis, and thresholding for an initial guess, followed by a custom optical flow algorithm for detecting the cell in subsequent frames. An orientation for the skeleton, required for a parametric fit, was induced using a nearest-neighbors algorithm and connecting disparate connected components according to local orientation and distance. A sweepline algorithm was used to determine the overall orientation. To measure the straightening rate, we analyzed a total of 60 cells which CurvatureTracker was able to track perfectly. CurvatureTracker oftentimes failed to track image sequences with multiple cells, excessive noise, poor resolution, or cells growing out-of-plane. By parametrically fitting the set of points T lying on the midline to a ninth-degree polynomial (x(t), y(t)) using MATLAB’s native fit function, we calculated the cell length using MATLAB’s native hypot function and the curvature according to $C={\displaystyle {\sum }_{t\prime \in T}|\frac{x^{\prime }(t)y^{″}(t)-y^{\prime }(t)x^{″}(t)}{{(x^{\prime }{(t)}^2+y^{\prime }{(t)}^2)}^{3/2}}{|}_{t=t^{\prime }}.}$ Since the ninth-degree polynomial fit may capture excessive curvature fluctuations within the mid-section of a cell, we repeated our analysis with a global arc fit to the midline. We found similar results for the global fit, which suggests a lack of substantial cell-substrate pinning or single-cell curvature fluctuations (Supplementary Fig. 8). Details of analyzing the MreB fluorescence experiments are provided in the Supplementary Methods.