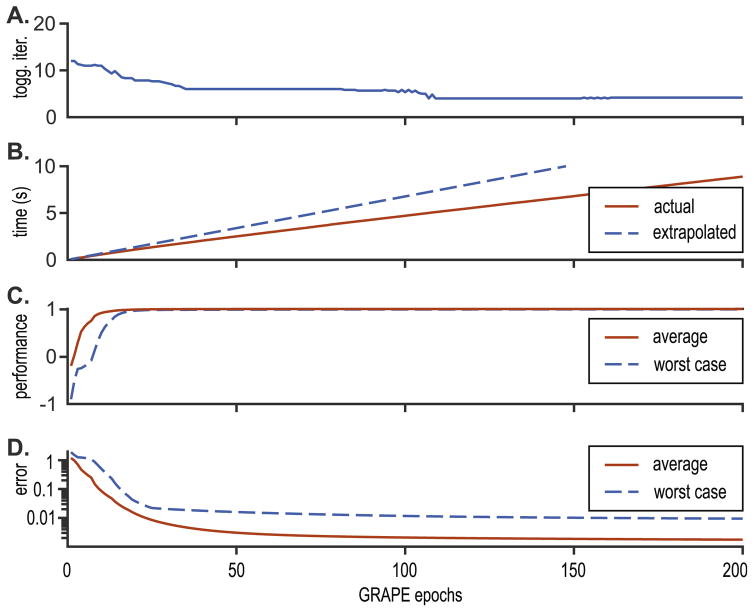
Fig. 2.

Grape in the toggling frame. A: The number of iterations of the toggling frame method that are needed to solve for the magnetization trajectory at each epoch of the GRAPE algorithm. This is the averaged over the 15 resonances in the computation. Clearly, near convergence, less computational effort is required. Note that only one toggling frame, q⃗(t), is stored for each of the 15 Hamiltonians, and it is being updated to remove time-varying terms introduced by Hamiltonian corrections. B: The time taken to find the pulse in terms of the number of epochs of GRAPE. If we extrapolate from the first few time points (dashed line) then the algorithm would take considerably longer. C: The performance metric ϕ converges to 1, both on average and for the worst performing resonance. D: The difference between ϕ and its theoretical maximum 1 tends towards zero, and all resonances are at least 99% aligned with the target state.