A test-retest study on Parkinson's PPMI dataset yields statistically significant white matter fascicles

Abstract

In this work, we propose a diffusion MRI protocol for mining Parkinson's disease diffusion MRI datasets and recover robust disease-specific biomarkers. Using advanced high angular resolution diffusion imaging (HARDI) crossing fiber modeling and tractography robust to partial volume effects, we automatically dissected 50 white matter (WM) fascicles. These fascicles connect deep nuclei (thalamus, putamen, pallidum) to different cortical functional areas (associative, motor, sensorimotor, limbic), basal forebrain and substantia nigra. Then, among these 50 candidate WM fascicles, only the ones that passed a test-retest reproducibility procedure qualified for further tractometry analysis. Leveraging the unique 2-timepoints test-retest Parkinson's Progression Markers Initiative (PPMI) dataset of over 600 subjects, we found statistically significant differences in tract profiles along the subcortico-cortical pathways between Parkinson's disease patients and healthy controls. In particular, significant increases in FA, apparent fiber density, tract-density and generalized FA were detected in some locations of the nigro-subthalamo-putaminal-thalamo-cortical pathway. This connection is one of the major motor circuits balancing the coordination of motor output. Detailed and quantifiable knowledge on WM fascicles in these areas is thus essential to improve the quality and outcome of Deep Brain Stimulation, and to target new WM locations for investigation.

Highlights

• •A diffusion MRI protocol to recover robust disease-specific biomarkers is proposed.
• •A test-retest reproducibility assessment is applied to 50 dissected WM fascicles.
• •Statistical analysis of tractometry results is performed on these robust fascicles.
• •Differences are found along the nigro-subthalamo-putaminal-thalamo-cortical pathway.
• •These results are crucial to improve existing treatments like Deep Brain Stimulation.

1. Introduction

The number of studies relying on tractography statistics has grown at a steady pace. While some are exploratory and use a single population dataset García-Gomar et al., 2016, Johnson et al., 2014, most compare healthy to non-healthy populations by either trying to find significant group differences Sharman et al., 2013, Yeatman et al., 2012, Dayan et al., 2016, Mole et al., 2016, Mezer et al., 2013, Son et al., 2016 or trying to classify subjects as being healthy or not through machine learning Kim and Park, 2016, Dyrba et al., 2015. These studies often focus on neurodegenerative diseases such as multiple sclerosis (MS) Dayan et al., 2016, Mezer et al., 2013, Alzheimer's disease (AD) Dyrba et al., 2015, Lo et al., 2010 or Parkinson's disease (PD) García-Gomar et al., 2016, Sharman et al., 2013, Mole et al., 2016, Kim and Park, 2016, Son et al., 2016.

One objective of such studies is to find a biomarker, i.e. a specific imaging signal characteristic whose presence is strongly correlated to a neurodegenerative disease. As such, several papers have shown that diffusion MRI (dMRI) and tractography can provide metrics sufficiently discriminative to be used as PD biomarkers Sharman et al., 2013, Ziegler et al., 2014, Mole et al., 2016, Son et al., 2016. Studies have looked at the effect of PD on motor pathways and the substantia nigra. Fractional anisotropy (FA) values were found to increase in the motor tracts (Mole et al., 2016) and decrease in the nigrostriatal and nigropallidal pathways (NSP) (Tan et al., 2015). Furthermore, increases in tract-density (Ziegler et al., 2014), free-water compartment (Ofori et al., 2015), mean diffusivity (MD) and radial diffusivity (RD) (Tan et al., 2015) were found around the substantia nigra. Some studies have tried to correct for free-water partial volume effect without identifying significant differences in free-water corrected FA in PD patients (Tan et al., 2015). Others have examined more closely sensorimotor connections within the cortico-basal ganglia thalamocortical system and found decreases of anatomical and functional connectivity in some of these regions (Sharman et al., 2013).

Unfortunately, many of these studies are based on small sample sizes, similar to AD studies before the creation of the ADNI (Alzheimer's Disease Neuroimaging Initiative) dataset.1 Another problem is that most existing studies are based on voxel-wise protocols and classical diffusion tensor imaging (DTI) metrics. Furthermore, studies all rely on the assumption that dMRI metrics as well as white matter (WM) fascicles are discriminant by nature. In other words, these studies assume that subjects of a homogeneous healthy group share a similar brain structure whose configuration is locally different from the brains of a group suffering from a neurodegenerative disease Sharman et al., 2013, Mole et al., 2016, Mezer et al., 2013. As a result, one usually concludes that a shift in the observed dMRI metrics is an indication of the disease. However, WM fascicles extracted from dMRI suffer from a certain level of noise and distortion as two tractography pipelines do not always produce the same results Wang et al., 2012, Kristo et al., 2013, Cousineau et al., 2016. This may be due to different preprocessing algorithms, different fiber tracking algorithms or hyperparameters, or simply the way the fascicles have been extracted (Côté et al., 2013). Also, dMRI is by nature a noisy and artefact-prone imaging modality (Descoteaux, 2015a). WM tracts and fascicles are thus vulnerable to accumulated noise and distortions in the many processing steps involved in population group analyses. Although this situation has been studied in the past, the fact that tractography results provide a distorted picture of the real anatomy of the brain has never been thoroughly investigated in applied WM studies. While some studies do integrate some sort of reliability assessment in their analysis Mezer et al., 2013, Mole et al., 2016, Yeatman et al., 2012, without state-of-the-art reliability measurements, one cannot disregard the hypothesis that statistically significant variations in diffusion measures may be due to the processing pipeline rather than an actual biological phenomenon.

In this paper, we propose a robust protocol for mining dMRI datasets and apply it to the Parkinson's Progression Markers Initiative (PPMI) (Marek et al., 2011) dataset. PPMI comes with a unique test-retest characteristic as subjects were scanned four times: twice initially, and twice one year later. This is a rare and a very powerful feature that can lead to more robust, reliable and reproducible tractometry and tract-based statistics.

Our approach involves a processing pipeline extracting dMRI metrics along WM fascicles. DTI- and HARDI-based metrics are extracted and projected on each fascicle to extract a vector of averaged metric values, sometimes called tract profile (Yeatman et al., 2012). We also propose a test-retest validation protocol to assess the reproducibility of these metrics and fascicles. While a simple procedure, we show that it is important to measure the inherent variability of the acquisition and processing pipelines, which directly affects the results of subsequent statistical analyses.

In this paper, we intend to answer the following questions:

• 1.How would one evaluate the test-retest reproducibility of dMRI metrics when projected to fascicles?
• 2.Can this serve to perform a tractometry population study on the PPMI dataset and are there any significant differences between the PD and healthy populations?

We found that not all of our extracted WM fascicles are reliable enough to be used in a population study. When comparing reliable fascicles of PD patients and healthy controls, we found statistically significant differences in regions located along the brainstem-substantia nigra-basal ganglia-motor cortex connections. Tract profiling reveals significant increases in FA, apparent fiber density, tract-density, and generalized FA detected for the nigro-subthalamo-putaminal-thalamo-cortical pathway. This connection is one of the major motor circuits balancing the coordination of motor output. In PD, overactivity of the striatum and subthalamic nucleus (STN) and pallidum due to striatal degeneration results in reduced activity of the motor cortex. Clinically, this phenomenon is reflected by hypokinesia, tremor and rigidity. Detailed anatomic knowledge and quantification of WM properties are of particular therapeutic importance for Deep Brain Stimulation (DBS), an invasive neuromodulatory therapy which aims to balance disorganized motor circuits by applying high-frequency current to a target nucleus within a motor circuit. In PD, the STN and GPi (globus pallidus internus) are most frequently targeted, and recent research from Vanegas-Arroyave et al. (2016) provides evidence for the involvement of WM fascicles in promoting the beneficial clinical effect. Thus, detailed and quantifiable knowledge of these WM fascicles is essential to improving DBS outcome.

2. Materials and methods

2.1. Tractometry processing pipeline

Our processing pipeline is illustrated in Fig. 1. At first, fiber ODFs are extracted with spherical harmonics of maximal order 8 using MRtrix 2 (a) (Tournier et al., 2012). DTI/HARDI metrics are then computed using the Dipy python package (Garyfallidis et al., 2014). These metrics are detailed in Table 2. Then, whole brain fODF deterministic tractography (b) is performed using MRtrix's streamtrack command with a step size of 0.5 mm and a total number of 500,000 streamlines. Seeding was performed with a WM mask coming from a T1 registered to the diffusion upsampled to 1 mm³. Next, WM pathways (c) are automatically dissected from the whole brain tractogram with TractQuerier (Wassermann et al., 2016) (queries available at https://github.com/martcous/ppmi-study). From this point on, each pathway is processed independently using our automated tractometry pipeline (d). Spurious streamlines (outliers) are removed using hierarchical QuickBundles (e) (Garyfallidis et al., 2017). As shown in Côté et al. (2015), outliers have a low density and are far in terms of shape distance from other streamlines in the fascicle. They can therefore be detected automatically, as detailed in 7.1 (Garyfallidis et al., 2012). Then, centroids are computed as a mean streamline of the pathway using the minimum-distance-flipped metric (f) (Garyfallidis et al., 2012). This centroid is subsampled to N = 20 equidistant points and every point of every streamline of the pathway is assigned to its closest centroid point (g). Metric values are then projected to these assignments masks and averaged in order to extract N averaged values along the pathway. Each voxel is weighted by its relative geodesic distance to the closest centroid point such that spurious streamlines far from the centroid do not affect the result as much. In the end, a tract profile is extracted for every combination of metrics and pathways (h).

Fig. 1.

Important steps of our processing pipeline illustrated on the corticospinal tract (CST). a) Raw dMRI images are processed. b) Whole brain deterministic tractography is performed. c) WM fascicles are extracted (CG in red, CST in blue, IFOF in green, SLF1 in yellow, UF in turquoise). d) Fascicles are processed independently (CST shown). e) Outliers are removed. f) Centroids are extracted. g) The fascicle is subsampled in 20 equidistant parts (colored independently). h) Tract profiles are computed (with standard deviation in gray). Note: In this example, the outlier removal threshold was slightly exaggerated in order to visually show its effect. In practice, the CST was not affected by the outlier removal. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Diffusion metrics included in this Parkinson study.

Type	Acronym	Metric	Description	Refs.
DTI	AD	Axial diffusivity	Diffusion rate along the principal diffusion axis (s/mm2).	Basser and Pierpaoli, 2011, Descoteaux, 2015b
	RD	Radial diffusivity	Average diffusion rate across radial axes (s/mm2).	Basser and Pierpaoli, 2011, Descoteaux, 2015b
	MD	Mean diffusivity	Average diffusion rate across every axis (s/mm2).	Basser and Pierpaoli, 2011, Descoteaux, 2015b
	FA	Fractional anisotropy	Anisotropy measure of the diffusion tensor.	Basser and Pierpaoli, 2011, Descoteaux, 2015b
	GA	Geodesic anisotropy	Geodesic anisotropy measure of diffusion.	Fletcher (2004)
	Mode	Tensor mode	Shape of the tensor (from planar to tubular [−1, 1]).	Kindlmann et al. (2007)
	Norm	Tensor norm	Norm of the diffusion tensor.	Kindlmann et al. (2007)
HARDI	GFA	Generalized fractional anisotropy	Generalized FA computed from the constant-solid angle q-ball reconstruction.	Aganj et al., 2010, Tuch, 2004
	AFD max	Maximal apparent fiber density	Maximal value of the fODF amplitudes.	Raffelt et al. (2012)
	AFD total	Total apparent fiber density	Spherical harmonic coefficient 0 of the fODF.	Raffelt et al. Raffelt et al., 2012, Raffelt et al., 2017
	NuFO	Number of fiber orientations	Number of local maxima of the fODF.	Dell’Acqua et al. (2013)
Tract-based	TDI	Tract-density imaging	Number of streamlines per voxel.	Calamante et al. (2010)

2.2. Reproducibility of white matter fascicles

As mentioned previously, dMRI is a noisy and artefact-prone modality. As such, tractography algorithms may return a distorted picture of the real WM anatomy. To produce meaningful statistics, one should take into consideration the level of distortion each fascicle is suffering from and use only pathways that are above a certain level of precision. Unfortunately, it is very difficult (if not impossible) to quantify to which extent a given WM fascicle (as well as its associated diffusion metrics) is distorted for a single subject. However, due to the multi-acquisition and multi-timepoint nature of PPMI, we can compute a test-retest score and measure the reproducibility of each fascicle. Although a reproducibility score does not explicitly account for tractography distortions per se, it nonetheless ensures the consistency of our dMRI pipeline. When a given subject undergoes two dMRI acquisitions within a short period of time with the same acquisition protocol, one can assume that tractography results should not vary much. The goal of our test-retest score is to measure the reproducibility of WM fascicles in terms of their shape and volume, as well as their tract profile. Following this test, we keep fascicles whose configuration is reproducible and thus reliable for a population study.

At first, our test-retest score measures the reproducibility of the fascicles' shape and volume. In that perspective, we compute the overlap of every fascicle extracted from each pair of acquisitions (two acquisitions at the baseline and two more one year later) both for healthy and PD subjects. To do so, we register the T1 of every subject to the MNI 2009 template (Fonov et al., 2009) using the ANTs non-linear registration software (Avants et al., 2008). The resulting registration function is applied to the WM fascicles obtained at step (e) of our processing pipeline (cf. Fig. 1) using TractQuerier's tract_math tool (Wassermann et al., 2016). Once every fascicle of every subject has been projected to the same space, we compute a slightly modified version of the Dice coefficient (Dice, 1945) which we call the weighted Dice coefficient. Let W_i be a fascicle extracted from a certain diffusion volume and W_j another fascicle extracted from another set of data. Note that in this study, W_i and W_j are the same fascicle but extracted from different diffusion data. The standard Dice coefficient between W_i and W_j is

$$D\left(W_i,W_j\right)=\frac{2{\sum }_v{\left(W_i\cap W_j\right)}_v}{{\sum }_v{W}_{i,v}+{\sum }_v{W}_{j,v}}$$ (1)

where W_i and W_j contain binary values (1 inside the fascicle and 0 otherwise) and v is a voxel index. As is, the Dice coefficient greatly penalizes for spurious streamlines that would be far from the core of the fascicle. Given that WM fascicles have more tracts in the middle than in their periphery, we propose a weighted Dice coefficient which accounts for the number of streamlines per voxel. In that perspective, each voxel in W_i and W_j contains a value between 0 and 1 expressing the fraction of tracts passing through that position. Our weighted Dice metric sums the voxels that overlap in W_i and W_j and divides by the total sum of voxels:

$$D\left(W_i,W_j\right)=\frac{{\sum }_{v^{\prime }}{W}_{i,v^{\prime }}+{\sum }_{v^{\prime }}{W}_{j,v^{\prime }}}{{\sum }_v{W}_{i,v}+{\sum }_v{W}_{j,v}},$$ (2)

where v′ stands for the voxels that are within the intersection of the W_i and W_j fascicles. Our weighted Dice gives more importance to areas with dense fibers.

We also quantify the test-retest reproducibility of the tract profiles. We assume that the tract profile of a given pathway should be closer to one from the same subject than one from any other subject. This procedure is illustrated in Fig. 2. Here, FA tract profiles of the corticospinal tract are shown in (a), and in (b), tract profiles of fascicle #2 described later as the connection between associative cortex and putamen. The first two profiles (green and blue) were extracted from two acquisitions of the same subject while the last one (in red) was extracted from another subject. In (a), we have the situation where the tract profiles of the first subject are more similar to each other than to the other subject chosen randomly. This is in line with intuition as the brain structure of an individual is more similar to itself than to that of another person. Conversely, in (b), we see that the tract profile of the first acquisition of the first subject is more similar to the tract profile of the other subject than to its second acquisition. In this case, the tractography pipeline induced a distortion to the fascicle that makes it unreliable for a population study. In this example, we would therefore remove fascicle #2 from the analysis.

Fig. 2.

Comparison of the FA tract profile of the corticospinal tract (CST) and fascicle #2, described in Table 1, from three different acquisitions: the first two from the same subject and the last one from a different subject. In (a), we have the desired case where the two intrasubject acquisitions are closer to each other than to the other subject's acquisitions, while in (b) we have the unfortunate case of the subject's first acquisition being closer to the other subject's acquisition than its second acquisition. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)

The goal of the test-retest tract profile score is to verify that intrasubject acquisitions are closer to each other than to other subjects' acquisitions. After z-score standardization using the mean and standard deviation of each point of each profile, an Euclidean distance is computed between all acquisition pairs of each subject. Since the PPMI dataset contains 179 healthy subjects and 412 PD all with 4 acquisitions (2 at the baseline and 2 one year later), we get to compute (412 + 179) * 4 − 1 = 2363 tract profile distances for each tract profile of each patient (more details on PPMI in Section 2.4). These distances were then averaged into two different values: (1) an intrasubject average distance, which includes distances of scan 1 of subject 1 vs scan 2–4 of subject 1, scan 2 of subject 1 vs scan 3–4 of subject 1, etc. and (2) an intersubject average distance, which included scan 1–4 of subject 1 vs scan 1–4 of subject 2–600, scan 1–4 of subject 2 vs scan 1–4 of subject 3–600, etc. Finally, these two values were subtracted from each other into what was called the average intersubject minus intrasubject tract profile distance. Thus, a single value for each fascicle studied was obtained. An ideal situation is where the difference would be high; then, the distance between same-subject tract profiles of this fascicle is much lower than the distance between different subjects. Should this difference be too small or even negative, the fascicle would be discarded from the study.

2.3. Statistical analysis

The tract profiles that passed the test-retest score are then applied to an hypothesis t-test. This is done to identify sections of the tract profiles that are significantly different between the PD and healthy controls. The Welch's unequal variances t-test (Zimmerman, 2004) was chosen to account for the difference in sample sizes between the two populations, as there were twice as many PD patients as healthy controls. To maximize the statistical robustness and account for multiple comparisons, each t-test was additionally performed in 10,000 permutations by sampling from the two populations. Furthermore, a corrected significance threshold was computed from the 10,000 permutation t-values (Nichols and Holmes, 2002). A t-test was considered statistically significant only if its p-value was lower than 0.05 and the absolute value of its t-value was higher than the computed threshold.

2.4. Parkinson's PPMI dataset

We used the T1 and diffusion-weighted images of the publicly-available Parkinson's Progression Marker Initiative (PPMI) dataset (Marek et al., 2011). This dataset contains 179 healthy control subjects and 412 patients recently diagnosed with PD. Note that for this study, we do not include the SWEDD (scans without evidence of dopaminergic deficit) and the prodromal subjects nor the genetic cohorts. PD and healthy patients have a mean age of 61 and 59 years respectively. More than 93% of the subjects are Caucasians, 71% of PD are male and 57% of healthy patients are male. PPMI dMRI data was acquired using a standardized protocol used on Siemens Tim Trio and Siemens Verio 3 Tesla MRI machines from 32 different international sites. Diffusion-weighted images were acquired along 64 uniformly distributed directions using a b-value of 1000 s/mm² and a single b = 0 image. Single shot echo-planar imaging (EPI) sequence was used (116 × 116 matrix, 2 mm isotropic resolution, TR/TE 900/88 ms, and twofold acceleration). An anatomical T1-weighted 1 mm³ MPRAGE image was also acquired. Each patient underwent two baseline acquisitions and two more one year later. The right and left-onset patients are distributed in proportions of 57% and 43%. More information on the MRI acquisition and processing can be found online: http://www.ppmi-info.org/.

2.4.1. Segmentation of white matter fascicles

Anatomical T1-weighted images are processed with the Biospective PIANO™ atlas-based segmentation tool. As illustrated in Fig. 3, cortical and subcortical areas can be automatically segmented, including the left and right substantia nigra (SN). Inspired by Sharman et al. (2013), we defined the WM fascicles in Table 1 and illustrated it in Fig. 4. In addition, we included the first parts of the corpus callosum (CC1-CC5) as well as the left-right cingulum and corticospinal tract. Note that this approach was also tried by Son et al. (2016) and the differences will be discussed later. The studied diffusion metrics are listed and briefly described in Table 2.

Fig. 3.

To extract specific WM fascicles, specific regions were segmented using an atlas, illustrated in (a) sagittal and (b) coronal view: , , , , 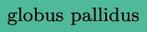and . Some fascicles extracted also connected various regions of the cortex which are illustrated in (c): , , , , and . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 1.

List of the 20 WM fascicles used for this study inspired from Sharman et al. (2013). All of these fascicles are in both left and right versions.

Fig. 4.

Some of the 20 specifically extracted WM fascicles in blue, named in Table 1. In (a), we have the fascicles connecting the cortex (fascicles #’s 1, 2, 3 and 18). In (b), we have the fascicles connecting the cortex (fascicles #’s 4, 5, 6 and 19). In (c), we have the fascicles connecting the cortex (fascicles #’s 7, 8, 9 and 20). Then, in the second row, we have the four fascicles connecting the 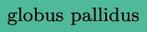(fascicles #’s 14 to 17). Fascicles #’s 10 to 13 are not shown because they were too short for proper visualization. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.5. Healthytest-retest dataset

Although PPMI images were acquired with the same acquisition protocol, the fact that they come from 32 different sites and MRI machines from different manufacturers creates unavoidably some distortions. To properly validate our test-retest protocol, we pre-acquired a test-retest dataset from 11 healthy subjects with 3 different timepoints (all within a week) at the same site, with the same technical team, and the same MRI machine. Diffusion-weighted images were acquired along 64 uniformly distributed directions using a b-value of 1000 s/mm² and a single b = 0 image. Single shot echo-planar imaging (EPI) sequence was used from a 1.5 Tesla SIEMENS Magnetom (128 × 128 matrix, 2 mm isotropic resolution, TR/TE 11,000/98 ms, and GRAPPA factor 2). An additional b = 0 image was acquired in reversed phase-encode direction to correct for susceptibility-induced distortions using FSL/TOPUP (Andersson et al., 2003). An anatomical T1-weighted 1 mm³ MPRAGE (TR/TE 6.57/2.52 ms) image was also acquired. Diffusion data was upsampled to 1 mm³ resolution using a trilinear interpolation and the T1-weighted image was registered to the upsampled b = 0 image. Quality control by manual inspection was used to verify the quality of the registration.

Major WM fascicles were segmented using Freesurfer (Fischl et al., 2004) and TractQuerier (Wassermann et al., 2016). Since these were extracted to validate our method, we report fascicles in common with the PPMI dataset namely, the arcuate fasciculus (AF), corpus callosum (CC), cingulum (CG), corticospinal tract (CST), inferior fronto-occipital fasciculus (IFOF), optic radiation (OR), and superior longitudinal fasciculus (SLF).

3. Results

3.1. Test-retest of the healthy dataset

The test-retest measures were first computed on our healthy dataset. Fig. 5 shows, in (a), a visual example of the overlap between two CST from different subjects (in red and blue), in (b), the volume overlap weighted Dice coefficient for all the fascicles, and in (c), the tract profile distance difference between intersubject and intrasubject. Note that these reproducibility results are considered optimal since they were computed from major WM fascicles on young, healthy subjects, acquired within the same week, with the same scanner, the same sequence, and the same technician. But despite this highly constrained acquisition protocol, some fascicles have a weighted Dice coefficient significantly lower than others (e.g. SLF1) while some have a tract profile distance that is suspiciously large. These observations highlight the fact that dMRI is by nature a noisy procedure that needs to be handled with care.

Fig. 5.

Our test-retest scores on our healthy dataset. In (a), the overlap of two CST from different subjects (in red and blue) are shown. Dice coefficient measures the overlap in purple. In (b), the average fascicle weighted Dice coefficient across all intrasubject and in (c) the average difference between the inter and intrasubject FA tract profile distance are plotted. The red line is the minimum value measured across all fascicles. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

According to these results, a threshold for a good weighted Dice coefficient can be set to 72% and a threshold for the tract profile distance intra and intersubject difference can be set to 3.2, two values corresponding to the lowest measured values (illustrated as the red lines in Fig. 5). In this study, we considered that a fascicle passed our test-retest reliability assessment when both their Dice coefficient and their tract profile distance difference were above these two thresholds.

3.2. Test-retest of the PPMI dataset

After having validated our test-retest procedure on the healthy dataset, we applied this methodology to the PPMI dataset on the fascicles of interest, namely the 20 identified in Table 1 as well as the corpus callosum (CC1-5), cingulum (CG left-right) and left-right corticospinal tracts (CST). Similar to Fig. 5, Fig. 6 shows the weighted Dice coefficient overlap in (a) and the distance difference between inter and intrasubject FA tract profiles in (b). First, we note the fairly good test-retest reproducibility of most large WM fascicles in common with the healthy dataset such as the CC1, CC2, CC4 and CST. However, Fig. 6 shows that more complex WM fascicles as defined in Table 1 are much less reproducible and this will be discussed later. When looking at both graphs of the figure, only fascicles #’s 14 to 16 seem reproducible out of the 20. Other fascicles were discarded from the tractometry analyses.

Fig. 6.

Our test-retest scores on the PPMI dataset. In (a), the average fascicle weighted Dice coefficient across all intrasubject and in (b) the average difference between the inter and intrasubject FA tract profile distance. The red line is the chosen threshold measured from the test-retest dataset in Fig. 5. Fascicles #1 to 20 refer to the fascicles introduced in Table 1. The bolded fascicles are the ones that are above both thresholds and therefore passed our test-retest assessment. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Moreover, we looked at the influence of volume reproducibility on the tract profiles inter and intrasubject distance difference. In other words, to what extent does fascicle overlap influence tract profiles specificity. The results and correlation are shown in Fig. 7. A clear linear correlation can be seen where fascicles with a good overlap have a higher chance of providing a better metric-based test-value score.

Fig. 7.

Average intra and intersubject tract profile distance difference given the average fascicle weighted Dice coefficient across all intrasubject acquisitions. A linear correlation is also shown.

3.3. Statistical analysis on segmented WM fascicles

Results of the permutation t-tests with significantly different regions are illustrated in Table 3. Recall that each fascicle was split in N = 20 different regions. Most significant regions had at least 2 or 3 direct neighbors significant as well. In Table 3, the arrows indicate whether PD patients metric values were higher (↑) or lower (↓) than healthy controls. Thicker arrows (⇑ and ⇓) signify that more than 25% of the 20 parts of the fascicle were significant. Among major trends, we found significant increases in fractional anisotropy (FA), generalized fractional anisotropy (GFA), geodesic anisotropy (GA), and maximal apparent fiber density (AFD max) for PD patients as compared with controls in pathways connecting the subsantia nigra. In these same pathways, we also found that these significant increases are driven by significant decreases in mean diffusivity (MD), radial diffusivity (RD) and tensor norm for PD patients. Finally, parts of the corpus callosum and corticospinal tracts had comparable trends in motor regions. While both hemispheres showed similar trends, statistically significant differences appeared more frequently in the left hemisphere.

Table 3.

Summary of the significant differences between populations. Only results with a p-value of <0.05 and a t-value bigger than the significance threshold are reported. The arrows indicate whether PD patients metric values were significantly higher (↑) or significantly lower (↓) than healthy controls. Thicker arrows (⇑ and ⇓) signify that more than 25% of the 20 parts of the fascicle were significant.

Type	Metric	Fascicles
DTI	AD	B15 ↓, CC1 ↓, CC2 ⇓, CC4 ↓, CST ↓
	FA	B14 ⇑, B15 ⇑, B16 ⇑, CC1 ↑, CC2 ↑, CC4 ↑, CST ⇑
	GA	B14 ⇑, B15 ⇑, B16 ⇑, CC1 ↑, CC2 ↑, CC4 ↑, CST ↑
	GFA	B14 ⇑, B15 ⇑, B16 ⇑, CC1 ↑, CC2 ↑, CC4 ↑, CST ⇑
	MD	B14 ⇓, B15 ⇓, B16 ⇓, CC1 ⇓, CC2 ⇓, CC4 ⇓, CST ⇓
	Mode	B14 ⇑, B15 ↑, B16 ↑, CC4 ↑, CST ↑
	Norm	B14 ⇓, B15 ⇓, CC1 ⇓, CC2 ⇓, CC4 ⇓, CST ↓
	RD	B14 ⇓, B15 ⇓, B16 ⇓, CC1 ⇓, CC2 ↓, CC4 ↓, CST ⇓
HARDI	AFD Max	B14 ⇑, B15 ⇑, B16 ⇑, CC1 ↓, CC2 ↓, CC4 ↓
	AFD Total	B14 ⇑, B15 ⇑, B16 ⇑, CC1 ⇓, CC2 ⇓, CC4 ⇓, CST ⇓
	NuFO	B14 ↓, B15 ↓, B16 ↓, CC1 ↓, CC2 ↓, CC4 ↓
Tract-based	TDI	B14 ⇑, B15 ⇑, B16 ↑, CST ↑

Selected combinations of fascicles and metric values with significant differences are shown in Fig. 8. These show representative results of most fascicles qualified by the test-retest and for at least one metric of interest. Yellow (p-value ≈ 0.10) to red (p-value ≈ 0.0001) regions indicate increases in PD populations (t-value > 0) while green (p-value ≈ 0.10) to pink (p-value ≈ 0.0001) regions indicate decreased values (t-value < 0). Smaller fascicles 14 to 16 have most of their regions significantly different between populations while bigger fascicles CC and CST have more localized differences.

Fig. 8.

Heatmap of p-values projected on different pathways of a specific subject. Yellow to red signifies higher metric values in PD subjects than controls, red values being the most significant (p-value very close to a perfect 0). Green to pink signifies lower metric values in PD subjects than controls, pink values being the most significant (p-value very close to a perfect 0). For the CC, the left of the figure signifies the left side of the patient. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.3.1. Studying the progression of the disease

Since the PPMI dataset contains two different timepoints, one at the baseline and another one year later, the progression of the disease was studied by separating the acquisitions in these two populations. The exact same metrics and fascicles were considered, and the same permutation t-test statistical analysis was performed. While similar trends as when comparing PD patients to healthy controls were found, none of them were statistically significant at p-value < 0.05.

4. Discussion

Our results are promising and confirm some existing trends Mole et al., 2016, Son et al., 2016. Significant differences between controls and PD groups are located along the brainstem, substantia nigra, basal ganglia and motor cortex connections. Tract profiling reveals that significant WM alterations between both groups appear within specific anatomic regions, namely the substantia nigra (SN), the striatum and subthalamic nucleus (STN), pallidum, putamen and thalamus. Here, we detect a significant increase in FA, apparent fiber density, tract-density, and generalized FA. These changes are also driven by a reduction in radial diffusivity and mean diffusivity. These phenomena are also present in the motor and premotor part of the CC and CST near the ends of the fascicles.

As mentioned earlier, the progression of the disease was also studied by comparing profiles of patients at the baseline timepoint and one year later. While nothing was statistically significant, similar trends than when comparing patients to healthy controls were found, which indicates that the disease indeed affects the regions highlighted in this paper. It is not significant perhaps because PD evolves slowly and one year is not enough to see major changes in specific regions. The PPMI dataset is planning to follow patients every year in order to acquire more timepoints. This will allow future studies to better research the progression of this disease.

4.1. Similarities with other processing pipelines

Our processing pipeline is quite similar to the automated fiber-tract quantification (AFQ) software (Yeatman et al., 2012). Both procedures extract tract profiles using the centroid of a fascicle. The main difference between the two, despite the fact that ours is written in Python and not in MATLAB, is that our pipeline does not require manual regions of interests (ROIs) nor a template for each WM fascicle to cut the extremities of fibers. Indeed, our pipeline keeps the WM tracts in the subjects native space, which means registration is not required once you have the fascicle extracted for computing tract profiles. In order to avoid any spurious parts not caught by our outlier removal processing step to affect the resulting profile, each voxel of the metrics are weighted by the geodesic distance to the closest centroid point and the number of streamlines that pass through this voxel. AFQ weighs instead at the fiber level by using the Mahalanobis of each fiber to the centroid.

4.2. Differences from similar Parkinson studies

The approach of comparing the tractography results extracted from the PPMI dataset using fascicles defined by Sharman et al. (2013) was also attempted in a paper by Son et al. (2016) published during the writing of this manuscript. That said, our approaches differ significantly, mainly on six aspects. First, as opposed to us, their analysis includes SPECT as well as dMRI images. Second, they correlated their results with a nonimaging metric/the clinical disease severity rating scale, namely MDS-UPDRS. Third, they used the older tractography method of FACT DTI as opposed to HARDI. This means that their tractography pipeline is less robust to fiber crossings and partial volume effects. Fourth, instead of using the entire PPMI dataset, they only used the baseline acquisition of 90 subjects. Fifth, while we studied many types of diffusion metrics, they only reported changes in the fiber density (FD), which is known to have several important limitations when considered as a quantitative measure (Calamante et al., 2015). This value was computed once per fascicle as opposed to a vector of values along the fascicle like our tract profiles. Finally, they have no test-retest validation protocol and, as such, of the 6 fascicles they found significant differences, 5 of them did not pass our test-retest analysis (namely fascicles 4, 5, 6, 11 and 12). This is not surprising since these fascicles are hard to define, have variable spatial extent and are hard to recover robustly. As more papers use dMRI tractometry to perform population statistics, it is important to remember that results are of value if the exact same regions of the brain are statistically compared. Given the strong anatomical priors injected in the segmentation of WM fascicles, test-retest is critical to assess the specificity and reproducibility of the extracted tracts.

However, similar to us, Son et al. did find significant differences for the putamen, globus pallidus and thalamus levels, which corresponds to 3 regions associated to our 3 most significant fascicles (fascicles 14, 15 and 16).

4.3. Limitations of the low b-value

In this study, acquisitions were done at a b-value of 1000 s/mm², which can be considered low. Higher b-values are usually recommended in high angular resolution diffusion imaging (HARDI) Tournier et al., 2007, Tuch et al., 2002. However, using spherical deconvolution with a properly data-driven response function Descoteaux et al., 2009, Tournier et al., 2007, high angular resolution and good fiber crossing reconstruction was achieved while maintaining a high signal to noise ratio of more classical DTI metrics derived from the b = 1000 data.

4.4. Choice of reproducibility metric

The Dice coefficient is a popular metric in the field of image segmentation Zijdenbos et al., 1994, Zou et al., 2004. To come up with a quantitative reproducibility assessment based on this coefficient, we had to choose a way to compare these different values among subjects. The first hurdle was that each subject did not have a consistent number of acquisitions. Some acquisitions failed our initial visual inspection because of excessive movement or major artifacts. Furthermore, most subjects had more than 2 acquisitions. This meant that many popular repeatability measures such as Bland and Altman's repeatability coefficient (Bland and Altman, 1986) or the intra-class correlation coefficient (Marenco et al., 2006) were not suited for this task. Instead, averaging all the combinations of intrasubject Dice coefficients proved to be the most versatile solution. The effect of multicenter acquisitions Friedman et al., 2008, Harrison et al., 2011 was not studied in the current work but would warrant a study of its own. In the end, we proposed a simple quality assessment criterion that could be easily implemented by a vast majority of population studies. The chosen Dice coefficient threshold was chosen empirically, but emphasis was not on the threshold itself but rather on the need to do such an assessment. The threshold can be adjusted to each study's needs.

4.5. Good reproducibility of major large WM fascicles

Due to the probabilistic nature of tractography, large and well-established WM fascicles in the literature are expected to be easier to extract from whole-brain tractograms, and therefore be more reproducible. Measuring the volume overlap of streamlines can result in dramatically low reproducibility in case the fascicle does not contain a minimum number of streamlines. It is nonetheless essential to assess streamline volumes, as tractometry projects metrics to volumes defined by these streamlines, and population statistics assume that we are comparing the exact same regions in the brain.

We first validated our reproducibility analysis using a dataset of healthy subjects and extracting major WM fascicles (Cousineau et al., 2016). We then replicated this analysis on the PPMI dataset, and got similar good results for the major WM fascicles included in this analysis. For example, the corticospinal tract (CST) scored a weighted Dice coefficient of over 90% in the healthy dataset and over 80% on the PPMI dataset. The difference can be explained by the fact that the PPMI dataset contains considerably older subjects and not all scanned within a few days like the healthy dataset. Despite being slightly lower, it remains a rather satisfactory reproducibility for the PPMI dataset. Generally, we considered Dice of over 70% satisfactory based on the lowest value obtained from the test-retest dataset.

4.6. Poorreproducibility ofsome WMfascicles

Several of the extracted fascicles based on Sharman et al. (2013) obtained quite poor reproducibility. For example, fascicle 7 connecting the sensorimotor cortex to the caudate got an overlap of under 20%. This can be explained by the fact that these fascicles connect small and deep nuclei (caudate, putamen, thalamus) to large functional cortical areas (associative, limbic, sensorimotor), which makes a good overlap very difficult to achieve. The poor reproducibility highlights a certain level of “ hardness to track” for these connections, even with advanced crossing fiber HARDI techniques. Furthermore, the regions they connect are quite complex such as the limbic cortical areas, the subcortical areas and the basal ganglia, and their area of termination depends on the quality of automatically segmented atlases. All of these factors are exacerbated by potential partial volume effects, motion, and poor resolution of acquisitions.

4.7. Clinical implications

Precise motor function relies on the balanced interplay of motor circuits, in which the basal ganglia plays a major coordinating role. The direct pathway, which facilitates movement by disinhibiting the thalamus, courses from the STN to the GPi (globus pallidus internus), the thalamus and to the cortex. The indirect pathway, on the other hand, inhibits movement by interposing the GPe (globus pallidus externus) as an additional relay station Alexander and Crutcher, 1990, Obeso et al., 2008a. The third, more recently discovered hyperdirect pathway, also inhibits movement along a direct connection from the STN to the cortex (Nambu et al., 2002).

The Parkinsonian state is characterized by neurodegeneration in the substantia nigra (SN), which leads to reduced dopaminergic input. As a result, overactivity of the STN and GPi enforces inhibition of thalamocortical motor pathways, which clinically presents as hypokinesia, tremor and rigidity (Obeso et al., 2008b).

Detailed knowledge of the WM changes in PD is essential in order to successfully modulate unbalanced motor circuits by Deep Brain Stimulation (DBS) (McIntyre et al., 2004). DBS is a gold standard therapy in drug refractory PD, which involves electrical stimulation of a target structure, most frequently the STN and GPi. There is evidence that the stimulation current not only affects the target structure, but spreads within adjacent axonal connections. Analysis of DBS electrodes in PD patients identified anatomic vicinity of clinically efficient electrodes and the substantia nigra, the thalamus and the brainstem (Vanegas-Arroyave et al., 2016). These regions correspond to the ones where we detect most significant FA changes in our study, implying the modulation of motor circuits. This finding is in accordance with previous studies, which detected alterations of diffusion parameters along the nigrostriatal circuit (Péran et al., 2010).

However, there remains some controversy concerning the role of striatal diffusion changes, in particular, FA changes in PD. Some studies detected a reduction in FA values Du et al., 2011, Péran et al., 2010, Vaillancourt et al., 2009, whereas others did not report on any significant FA alterations Esterhammer et al., 2015, Schwarz et al., 2013 or FA increases (Wang et al., 2011). A systematic review on all studies of FA changes revealed methodological differences as the main reason accounting for the divergent results, such as selection of ROI size, disease duration among patients and number of diffusion directions (Schwarz et al., 2013). In our study, these methodological differences are overcome by careful test-retest qualification of the fascicles of interest and tractometry of an extensive list of DTI, HARDI and tract-based metrics.

Pathophysiologically, PD is characterized by a progressive neurodegenerative process leading to nigral iron accumulation Lotfipour et al., 2012, Sian-Hülsmann et al., 2011, which was seen to increase FA values (Awasthi et al., 2010). Another possible mechanism of FA increase may be the progressive degeneration of the nucleus and subsequent invasion by adjacent fiber tracts (Lenfeldt et al., 2015). These effects could explain our significant increases and decreases observed in the diffusion metrics.

4.8. Interpretations of diffusion measure changes

The biological interpretation of diffusion measure changes is extremely challenging (Jones et al., 2013). While the trends of the changes can be understood and well explained in terms of the fundamentals of diffusion tensor modeling and other local reconstruction methods, such as the increased FA and apparent fiber density driven by reduction of radial and mean diffusivity, it is very hard to specifically apply a biological interpretation to these diffusion measure changes. Potential explanations for the increased FA in PD include: i) increased fiber density caused by axonal hypertrophy, ii) decreased fiber density on crossing pathways to the main motor connections from SN to motor cortex, and iii) alterations of the extra-cellular space (e.g. due to neuroinflammation).

In order to further probe these possibilities, it is necessary to go beyond single b-value high angular resolution diffusion imaging. Advanced diffusion imaging and sophisticated modeling with multiple shells and multiple diffusion times Burcaw et al., 2015, Fick et al., 2015, Nilsson et al., 2009, Nilsson et al., 2013, Szczepankiewicz et al., 2016, Zhang et al., 2012 may bring new answers in the near future and show the way to better interpretations. Further, imaging-pathologic correlations in appropriate animal models of PD would serve to further elucidate the biological underpinnings of the diffusion alterations.

5. Conclusion

We have established a reliable dMRI protocol for extracting robust disease-specific biomarkers. By taking advantage of the multi-timepoint aspect of the PPMI dataset and using state-of-the-art processing methods, we have computed reliable DTI and HARDI diffusion metrics along WM fascicles connecting motor and pre-motor regions from the basal ganglia, substantia nigra and brainstem. Using robust permutation statistics to compare healthy controls and PD populations, we have found statistically significant discriminant regions confirming existing literature. Tract profiling reveals that these changes do not appear everywhere along the WM fascicles, but are rather localized in precise and reproducible locations. There were significant increases in FA, apparent fiber density, tract-density, and generalized FA in the central part of connections between basal ganglia and substantia nigra as well as the extremities of the motor and premotor part of the corpus callosum and corticospinal tract. These WM integrity changes are driven by a reduction in radial diffusivity and mean diffusivity.

Our confidence in these findings was confirmed by our proposed test-retest reproducibility measures that assess the reliability of extracted WM fascicles, and we stress the importance of future tract-based population studies to perform a similar analysis before reporting any statistics. The design of dataset for tractometry studies should consider test-retest acquisitions to assess variability of measurements.

Appendix A. Supplementary materials

Supplementary materials.