Figure 10.

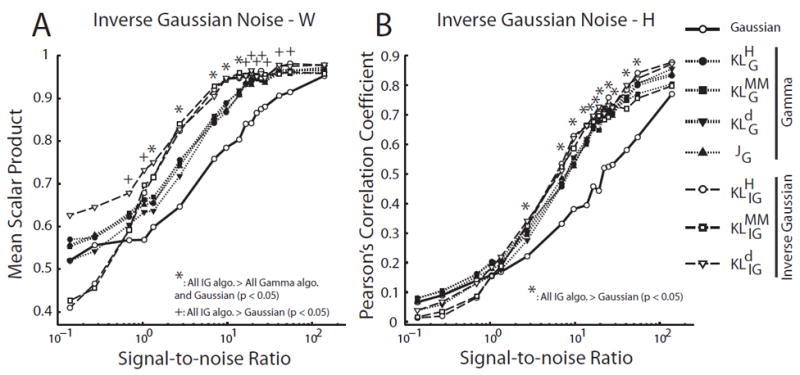
The inverse Gaussian NMF algorithms outperformed the Gaussian- and gamma-based NMF algorithms in data sets corrupted by inverse Gaussian noise. We evaluated the performance of each algorithm in simulated data sets (N = 10) generated by known W (15 × 5 matrix) and H (5 × 5000 matrix), but corrupted by random inverse Gaussian (IG) noise at different signal-to-noise ratios (SNR). A, Performance of NMF algorithms in identifying the basis vectors (W). Performance of each algorithm in each data set was quantified by the scalar product between the extracted vectors and the original vectors, averaged across the 5 basis vectors in the W matrix. Shown in the plot are mean scalar product values, defined as above, averaged across 10 simulated data sets. At moderate noise levels, IG-based algorithms clearly outperformed both the Gaussian and gamma algorithms (*; Student’s t-test; p < 0.05); at high and low noise levels, IG-based algorithms still performed better than the Gaussian (but not the gamma) algorithm (+; p < 0.05). B, Performance of the NMF algorithms in identifying the coefficients (H). Performance of each algorithm in each data set was quantified by the Pearsons correlation coefficient (ρ) between the extracted coefficients and the original coefficients (over a total of 5 × 5000 = 25,000 values). Shown in the plot are ρ values averaged across the 10 simulated data sets. IG-based algorithms outperformed the Gaussian NMF over a wide range of SNR (*; p < 0.05).