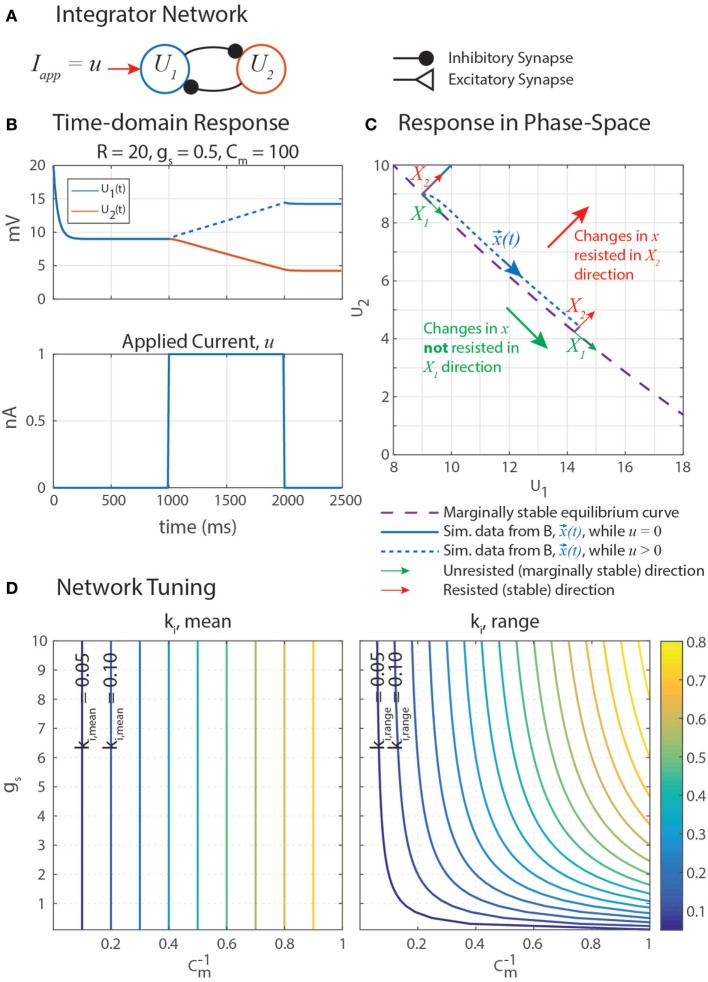
Figure 5.

(A) A disinhibitory network can exploit neural dynamics to compute the integral of an incoming signal. (B) When given an applied current in the form of a step, the network response is a ramp whose slope is proportional to the amplitude of the step. (C) A plot of this data in the (U₁, U₂) phase space shows that when stimulated by applied current u, the system state, x(t) = [U₁(t), U₂(t)]^T (blue), moves in the X₁ direction (green) while maintaining a constant distance from the equilibrium subspace (dashed violet) in the X₂ direction (red). This difference in behavior in each direction is because the eigenvalue associated with eigenvector X₁, λ₁ = 0, and the eigenvalue associated with eigenvector X₂, λ₂ < 0. X₁ and X₂ are drawn in multiple places because they depend on x(t), as shown in Appendix. (D) The mean rate of integration, k_i,mean (left), and the range of the rate of integration, k_i,range (right), depend on the synaptic conductance of mutual inhibition, g_s, and the membrane capacitance of the neurons, C_m. Note that the x-axis of these plots are 1/C_m, to better space the contour lines.