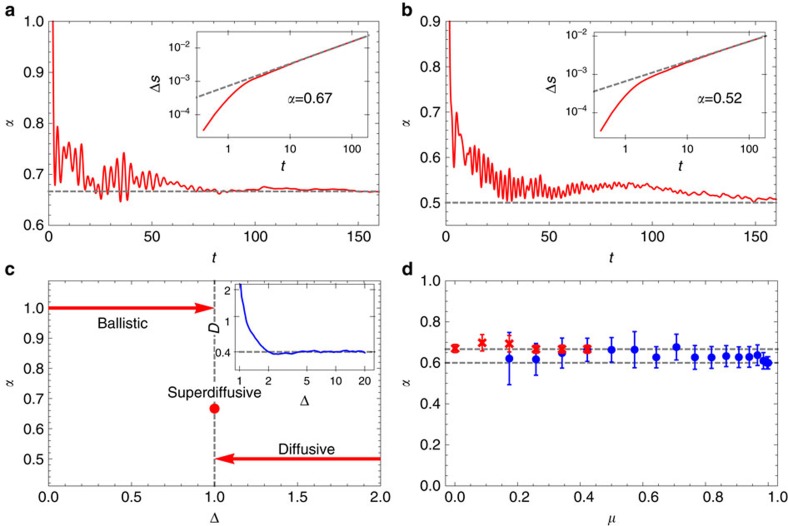
Figure 2. Scaling exponents of magnetization spreading.

(a,b) Local exponent α(t) calculated as a numerical log-derivative d log Δs(t)/d log t for Δ=1 (a) and Δ=2 (b) (dashed lines indicate exponents 2/3 and 1/2, respectively, while dashed lines in the insets show best power-law fits to Δs(t)—red curve), both for μ=π/1,800. (c) Conjecture for the dependence α(Δ) at high temperatures and small μ. The inset shows the diffusion constant obtained from Fick’s law for various values of Δ in the diffusive regime, converging to a finite value at large Δ (agreeing with ref. 28). (d) Dependence on μ for Δ=1 shows a small but significant change in the behaviour: for μ≈1 it is closer to α=3/5 while for small μ it becomes close to α=2/3 (dashed). The blue (circles) and red (crosses) symbols represent wave function and density operator evolutions respectively. We average over samples of 10–130 random initial wave-functions for each blue data point. For intermediate μ the error-bars (denoting the estimated s.d.) are larger since the simulation is less efficient in that regime (Methods section).