Focusing light inside dynamic scattering media with millisecond digital optical phase conjugation

Abstract

Wavefront shaping based on digital optical phase conjugation (DOPC) focuses light through or inside scattering media, but the low speed of DOPC prevents it from being applied to thick, living biological tissue. Although a fast DOPC approach was recently developed, the reported single-shot wavefront measurement method does not work when the goal is to focus light inside, instead of through, highly scattering media. Here, using a ferroelectric liquid crystal based spatial light modulator, we develop a simpler but faster DOPC system that focuses light not only through, but also inside scattering media. By controlling 2.6 × 10⁵ optical degrees of freedom, our system focused light through 3 mm thick moving chicken tissue, with a system latency of 3.0 ms. Using ultrasound-guided DOPC, along with a binary wavefront measurement method, our system focused light inside a scattering medium comprising moving tissue with a latency of 6.0 ms, which is one to two orders of magnitude shorter than those of previous digital wavefront shaping systems. Since the demonstrated speed approaches tissue decorrelation rates, this work is an important step toward in vivo deep-tissue non-invasive optical imaging, manipulation, and therapy.

1. INTRODUCTION

In opaque media, such as biological tissue, the heterogeneous refractive index distribution causes light to scatter, which makes the media look opaque and prevents us from focusing light deep inside the media to achieve optical imaging and manipulation [1,2]. Hence, the ability to focus light inside scattering media could revolutionize biophotonics by enabling deep-tissue non-invasive fluorescence microscopy, optical tweezing, optogenetics, micro-surgery, and phototherapy.

To focus light through or inside highly scattering media, various wavefront shaping approaches are being actively developed [3–6], including feedback-based wavefront shaping [7], transmission matrix measurement [8,9], and optical time reversal/optical phase conjugation (OPC) [10–13]. Among these techniques, OPC is most promising for in vivo applications because it achieves the shortest average mode time [14] (the average operation time per degree of freedom) by determining the optimum wavefront globally instead of stepwise. Although analog OPC based on nonlinear optics can be fast [15], digital OPC (DOPC) has a much higher fluence reflectivity and is capable of synthesizing a light field [14,16–19], thus becoming more useful and powerful. Recently, DOPC has enabled light focusing through ex vivo chicken tissue and tissue-mimicking phantoms up to 9.6 cm thick [20].

However, DOPC has been limited by the low speeds of cameras, data transfer, data processing, and spatial light modulators (SLMs). The low speeds prevent DOPC from being applied to thick living biological tissue, because the motion of the scatterers inside tissue causes the speckles on the phase conjugate mirror (camera + SLM) to decorrelate (on a time scale of 0.1–10 ms [15,21–23]) and breaks the time reversal symmetry. Although a bit-efficient, sub-millisecond wavefront measurement method was developed based on a lock-in camera [24], the net speed of the system was limited by the low speed of data transfer and wavefront modulation. Recently, a fast DOPC system controlling 1.3 × 10⁵ optical degrees of freedom was developed, and it focused light through scattering media with an effective latency of 5.3 ms and a total system runtime of 7.1 ms [23]. The system employed a single-shot wavefront measurement method, a field programmable gate array (FPGA) for data processing, and a digital micromirror device (DMD) for fast modulation. However, the reported single-shot wavefront measurement method does not work when the goal is to focus light inside, instead of through, highly scattering media. For biomedical and many other applications, focusing light inside scattering media is much more useful and difficult than focusing light through scattering media. The use of a DMD also imposes several limitations, which will be explained in the next section.

Here, we develop a simpler DOPC system that focuses light not only through, but also inside, scattering media. For the first time in the wavefront shaping field for focusing light through/inside scattering media [3–6], we employ a ferroelectric liquid crystal based SLM to achieve binary-phase modulation for high speed and high focusing quality. To take full advantage of the SLM and further improve the speed of ultrasound-guided DOPC, we develop a double-exposure binary wavefront measurement method. The speed of our system is one to two orders of magnit ude higher than those of previous ultrasound-guided DOPC systems [16,24–31], and our method achieves the fastest light focusing inside a scattering medium among all the digital wavefront shaping methods developed to date [3–6].

2. METHODS

A. Binary-Phase Modulation Based High-Speed Wavefront Shaping Enabled by a Ferroelectric Liquid Crystal Based SLM

DOPC focuses light through or inside scattering media by phase conjugating the scattered light emitted from a guide star. Specifically, a digital camera is used to measure the wavefront of the scattered light with digital holography. Then, an SLM, with pixels that are one-to-one matched with the pixels of the camera by a camera lens, is used to reconstruct the conjugate wavefront of the scattered light to achieve optical phase conjugation/time reversal [11,12,23,24,32–34]. In most wavefront shaping experiments, nematic liquid crystal based SLMs (NLC-SLMs) are used for phase modulation [7–9,11,12]. However, the latency of NLC-SLMs (typically tens of milliseconds [14,21], including the response time of the molecules and the data transfer time) is much longer than the speckle correlation time associated with living biological tissue. To increase the speed, DMDs have been employed to achieve high-speed wavefront shaping [23,35–40]. However, DMDs have several limitations for this application: (a) They typically achieve binary-amplitude modulation, which results in a lower focusing contrast compared with that of phase modulations. (b) The optical fluence threshold causing DMDs to malfunction under pulsed laser illumination is usually lower than that of liquid crystal based SLMs [41,42]. (c) The alignment of a DMD-based DOPC system is significantly complicated by the oblique reflection angle of the DMD [23]. (d) Although a loaded pattern can be displayed at ~23 kHz on a DMD, transferring a pattern from a PC or an FPGA board to the DMD can take 1.6–4.5 ms [23,38,40], limiting the speed of a DOPC system.

To overcome the above drawbacks of DMDs and NLC-SLMs, we developed a high-speed DOPC system using a ferroelectric liquid crystal based SLM (FLC-SLM, A512-P8, Meadowlark Optics, 512 × 512 pixels, 15 μm pixel size), which has a net latency of ~1 ms including the data transfer time. Specifically, it takes ~0.6 ms to transfer a pattern from a PC to the SLM using a PCI Express ×4 interface, and the response time of the FLC molecules is ~0.45 ms. Unlike NLC-SLMs that modulate the phase of the light field on each SLM pixel by a value between 0 and 2π, FLC-SLMs modulate the phase of the light field by only 0 or π(binary-phase modulation). Since in principle only one bit per pixel needs to be transferred to an FLC-SLM from a PC, while eight bits per pixel needs to be transferred to an NLC-SLM, the use of FLC-SLMs can reduce the data transfer load by eight times and thus increase the data transfer speed.

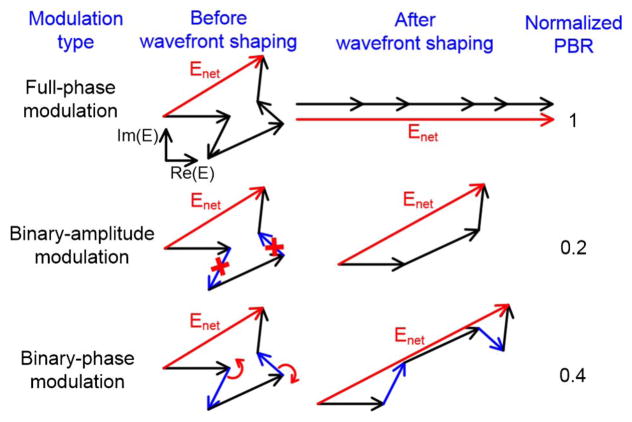
Figure 1 shows a comparison of different wavefront modulation schemes. Without shaping the wavefront of the input light, the light field at a targeted location inside a scattering medium is a random phasor sum. In conventional wavefront shaping, an NLC-SLM rotates each phasor to align them so that they constructively interfere and form a focus. A DMD, alternatively, achieves wavefront shaping by binary-amplitude modulation—it turns off those “bad” phasors that destructively interfere with the net phasor formed by the rest of the phasors. In contrast, instead of turning off the “bad” phasors, an FLC-SLM rotates the “bad” phasors by 180°, making them constructively interfere with the net phasor formed by the rest. In this way, FLC-SLMs double the focal peak-to-background ratio (PBR, which quantifies the focusing contrast), compared with DMDs [14,43,44] (see Supplement 1 for a derivation of the theoretical PBR for binary-phase modulation based wavefront shaping). Although the PBR achieved by FLC-SLMs is 40% of that achieved by NLC-SLMs that achieve full-phase modulation, the response time of FLC molecules (0.04–0.45 ms) is much shorter than that of NLC molecules, because FLC molecules have spontaneous electric polarizations that enable them to respond quickly to an external electric field [45].

Fig. 1.

Comparison of different wavefront modulation schemes in wavefront shaping. PBR, peak-to-background ratio.

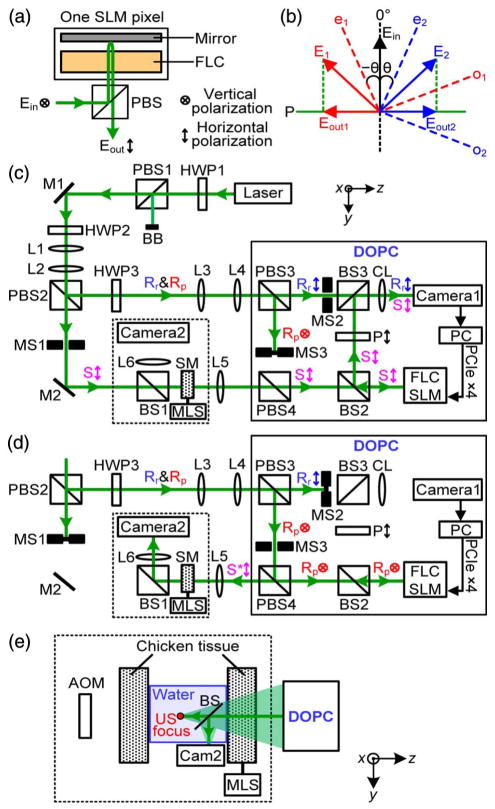
Figures 2(a) and 2(b) show how an FLC-SLM achieves binary-phase modulation. The SLM works in reflection mode. While the FLC layers act as a quarter-wave plate, the net result for round-trip light propagation is that each SLM pixel acts as a half-wave plate, whose optic axis orientation is electrically controllable between two states that are 2 θ apart [θ = 22.5°, see e₁ and e₂ in Fig. 2(b)]. To achieve binary-phase modulation, the polarization direction of the incident light field bisects the two states of the optic axis, that is, along the vertical direction. By reflection off an SLM pixel, the polarization of the light field is rotated to along either −45° or +45°, depending on the orientation of the optic axis. After passing through a linear polarizer, with an axis along the horizontal direction, the output electric field is either along −90° or +90° for the two optic axis states, with the same amplitude [Fig. 2(b)]. In this way, an FLC-SLM achieves binary-phase modulation. For reflection-mode FLC-SLMs, the linear polarizer is usually replaced by a polarizing beam splitter [Fig. 2(a)]. It should be noted that the FLC-SLM requires vertically polarized incident light, while the output binary wavefront corresponds to horizontally polarized light.

Fig. 2.

DOPC using a ferroelectric liquid crystal based spatial light modulator (FLC-SLM). (a) Each FLC-SLM pixel acts as a half-wave plate. PBS, polarizing beamsplitter. (b) Optic axis orientation can be switched between two states, e₁ and e₂, to achieve binary-phase modulation of the incident light E_in θ = 22.5°. (c) Schematic of the setup during wavefront recording for DOPC-based light focusing through scattering media. BB, beam block; BS, beamsplitter; CL, camera lens; DOPC, digital optical phase conjugation; HWP, half-wave plate; M, mirror; MLS, motorized linear stage; MS, mechanical shutter; PC, personal computer; PCIe ×4, peripheral component interconnect express interface with four lanes; SM, scattering medium; S, sample beam; S^*, phase-conjugated sample beam; and R_r and R_p, reference beams for wavefront recording and playback. The distance between SM and L6 (f = 100 mm) is 40 cm. (d) Schematic of the setup during wavefront playback for DOPC-based light focusing through scattering media. (e) Schematic of the setup for focusing light inside a scattering medium comprising two pieces of chicken tissue with ultrasound-guided DOPC. A complete schematic can be obtained by replacing the components enclosed in the dashed box in (c) and (d) with the components enclosed in the dashed box in (e). The acousto-optic modulator (AOM) is used only during wavefront recording. During wavefront playback, to verify that light is focused to the ultrasonic (US) focus, a beamsplitter (BS) reflects the focal pattern onto Camera2 (Cam2). To control the speckle correlation time on the SLM plane, a MLS moves the second piece of tissue at different speeds during the entire DOPC process (including both wavefront measurement and playback). The distance between the two pieces of tissue is 32 mm, and the distance between the ultrasonic focus and the tissue on the right side is 20 mm.

B. Experimental Setup and Methods for Fast Binary Wavefront Measurement

Using an FLC-SLM, we developed a DOPC system to focus light through [Figs. 2(c) and 2(d)] or inside [Fig. 2(e)] scattering media. In Fig. 2(c), the output of a continuous-wave laser (1 W, 532 nm, Verdi V10, Coherent) was split into a sample beam (S) and two planar reference beams (R_r and R_p, for wavefront recording and playback, respectively). S was first scattered by a scattering medium. Then, to measure the wavefront of the scattered light field along the horizontal polarization direction, we let the scattered light interfere with horizontally polarized R_r on Camera1 (pco-edge 5.5, PCO Tech, 500 μs exposure time). To obtain the binary-phase map for focusing light through scattering media, we used the single-shot binary-phase retrieval method [23]. Specifically, the interference pattern between S and R_r is written as $I(\overrightarrow{r})=I_{\mathrm{S}}(\overrightarrow{r})+I_{\mathrm{R}}(\overrightarrow{r})+2\sqrt{I_{\mathrm{R}}(\overrightarrow{r})I_{\mathrm{S}}(\overrightarrow{r})}cos[{\phi }_{\mathrm{S}}(\overrightarrow{r})-{\phi }_{\mathrm{R}}(\overrightarrow{r})]\approx I_{\mathrm{R}}(\overrightarrow{r})+2\sqrt{I_{\mathrm{R}}(\overrightarrow{r})I_{\mathrm{S}}(\overrightarrow{r})}cos[{\phi }_{\mathrm{S}}(\overrightarrow{r})-{\phi }_{\mathrm{R}}(\overrightarrow{r})]$, where I_S and I_R are the intensities of S and R_r impinging on each camera pixel at position r⃗; I_R ≫ I_S in this experiment; φ_S and φ_R are the phases of S and R_r, and φ_R is assumed to be a constant. I_R(r⃗) is not dependent on the dynamics of the sample and can be measured separately by blocking the sample beam before starting DOPC experiments. Then, the binary-phase map of S is obtained by

$${\phi }_{\mathrm{S}}(\overrightarrow{r})=\{\begin{array}{ll}0,\hfill & \text{if}I(\overrightarrow{r})\ge I_{\mathrm{R}}(\overrightarrow{r})\hfill \\ \pi ,\hfill & \text{if}I(\overrightarrow{r})<I_{\mathrm{R}}(\overrightarrow{r})\hfill \end{array},$$ (1)

where a constant phase offset φ_R is ignored. To achieve phase conjugation, a pre-calibrated binary-phase map to compensate for the curvatures of R_r, R_p, and the SLM was added to the phase map φ_S(r⃗) [46], and the resulting binary-phase map was displayed on the FLC-SLM to modulate the wavefront of R_p [Fig. 2(d)]. After reflecting off the FLC-SLM and passing through polarizing beams plitter PBS4, R_p became phase conjugate to the horizontal component of the scattered light field S exiting the scattering medium. After propagating through the scattering medium, R_p became a collimated beam and was focused by lens L6 onto Camera2 (GS3-U3-23S6M, Point Gray, exposure time = 1 ms).

To focus light inside, rather than through, scattering media, focused ultrasound was used as a guide star for DOPC, and this ultrasound-guided OPC is known as time-reversed ultrasonically encoded (TRUE) optical focusing [25,26,47]. Figure 2(e) is a schematic of the setup for focusing light inside a scattering medium comprised of two pieces. A complete schematic can be obtained by replacing the components enclosed in the dashed box in Figs. 2(c) and 2(d) with the components enclosed in the dashed box in Fig. 2(e). During wavefront recording, the sample beam S was first frequency up-shifted by 50 MHz by an acousto-optic modulator (AOM-505AF1, IntraAction) before it illuminated the scattering sample. After being scattered by the first piece of the scattering medium, a portion of the light passing through the ultrasonic focus was frequency down-shifted by 50 MHz because of the acousto-optic effect [48,49] (the frequency of the ultrasound was 50 MHz) and further scattered by the second piece of the scattering medium [Fig. 2(e)]. These ultrasonically tagged photons formed a stable hologram on Camera1 when interfering with the reference beam R_r by Camera1 can be written as $I(\overrightarrow{r})=I_{\mathrm{R}}(\overrightarrow{r})+I_{\mathrm{T}}(\overrightarrow{r})+I_{\mathrm{U}}(\overrightarrow{r})+2\sqrt{I_{\mathrm{R}}(\overrightarrow{r})I_{\mathrm{T}}(\overrightarrow{r})}cos[{\phi }_{\mathrm{T}}(\overrightarrow{r})-{\phi }_{\mathrm{R}}(\overrightarrow{r})]$, where I_T and I _U are the intensities of the ultrasonically tagged and untagged light (I_U ≫ I_T for highly scattering media) and φ_T is the phase of the ultrasonically tagged light that we want to measure. To use the single-shot wavefront measurement method [23] to obtain φ_T, $\sqrt{I_{\mathrm{R}}(\overrightarrow{r})I_{\mathrm{T}}(\overrightarrow{r})}\gg I_{\mathrm{U}}(\overrightarrow{r})$ must be satisfied. However, this condition is generally not satisfied for highly scattering media unless using an excessively high I_R, which would dramatically reduce the signal-to-background ratio and the signal-to-noise ratio [24,26,29]. Thus, the single-shot wavefront measurement method cannot be used here. To measure the phase map at maximum speed by minimizing the number of holograms recorded, we developed a double-exposure binary wavefront measurement method, which also works well with FLC-SLMs that perform binary-phase modulation. Specifically, we record two frames when the focused ultrasound was applied. However, in the second frame, the initial phase of the ultrasound was shifted by π. Mathematically, the intensities on each pixel of Camera1 recorded in the two frames can be written as $I_1(\overrightarrow{r})=I_{\mathrm{R}}(\overrightarrow{r})+I_{\mathrm{T}}(\overrightarrow{r})+I_{\mathrm{U}}(\overrightarrow{r})+2\sqrt{I_{\mathrm{R}}(\overrightarrow{r})I_{\mathrm{T}}(\overrightarrow{r})}cos[{\phi }_{\mathrm{T}}(\overrightarrow{r})-{\phi }_{\mathrm{R}}(\overrightarrow{r})]$ and $I_2(\overrightarrow{r})=I_{\mathrm{R}}(\overrightarrow{r})+I_{\mathrm{T}}(\overrightarrow{r})+I_{\mathrm{U}}(\overrightarrow{r})+2\sqrt{I_{\mathrm{R}}(\overrightarrow{r})I_{\mathrm{T}}(\overrightarrow{r})}cos[{\phi }_{\mathrm{T}}(\overrightarrow{r})+\pi -{\phi }_{\mathrm{R}}(\overrightarrow{r})]$. Then, the binary-phase map of the ultrasonically tagged light can be obtained by

$${\phi }_{\mathrm{T}}(\overrightarrow{r})=\{\begin{array}{ll}0,\hfill & \text{if}{I}_1(\overrightarrow{r})\ge I_2(\overrightarrow{r})\hfill \\ \pi ,\hfill & \text{if}{I}_1(\overrightarrow{r})<I_2(\overrightarrow{r})\hfill \end{array},$$ (2)

where a constant phase offset φ_R is ignored. To generate two bursts of ultrasound that have a π shift in the initial phase, we used an RF switch (ZASWA-2-50DR+, Mini-Circuits) to sequentially enable the outputs of the two channels of a function generator. Each channel generated a burst of sinusoidal waves with an amplitude of 80 mVpp, and the initial phases of the bursts generated by the two channels differed by π. By using this approach, we avoided an unwanted amplitude change when using an RF phase shifter. The output of the RF switch was amplified by a power amplifier (25A250A, Amplifier Research) with a gain of 54 dB, to drive an ultrasonic transducer (V358-SU, Olympus, with a lab-made lens having a numerical aperture of 0.4). During wavefront playback, to verify that light was focused to the ultrasonic focus by phase conjugation, a beamsplitter was used to reflect the focal pattern onto Camera2 [Fig. 2(e)]. This configuration allowed us to study the effect of medium decorrelation on the quality of the phase-conjugated focus, because we could move the scattering medium at different speeds during the entire DOPC process while monitoring the corresponding focusing quality (see Section 3.C). In our experiments, a program written in C/C₊₊ (see Supplement 1) calculated the phase map and controlled the cameras, the FLC-SLM, and a multifunction data acquisition card (PCIe 6363, National Instruments) for trigger generation.

C. Total System Runtime and Effective System Latency

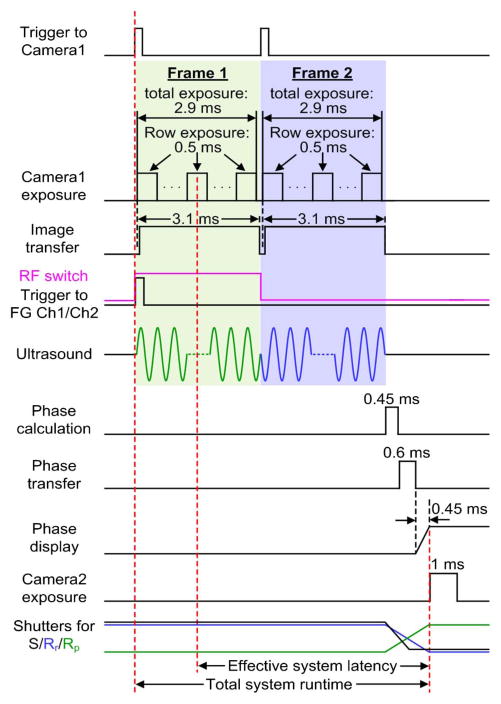
The total system runtime, defined as the time between when Camera1 starts recording to playback of the wavefront, is 4.7 ms for focusing light through scattering media with the single-shot binary-phase retrieval method. The total system runtime is 7.7 ms for focusing light inside scattering media with the double-exposure binary-phase retrieval method (see the workflow in Fig. 3). However, the effective system latency is shorter than the total system runtime [23], since a rolling shutter was used in Camera1 to achieve a higher frame rate during wavefront recording. With the rolling shutter, the top and bottom halves of the image sensor expose and read out simultaneously in a row by row manner from the edge to the center of the sensor, and neighboring rows are exposed successively with a 9.17 μs delay in the start time. Since the central 520 rows on the sensor of Camera1 were used in our experiments, the effective system latencies, calculated from the average exposure start time of the camera sensor to the playback of the wavefront, are 3.5 ms and 6.5 ms for focusing light through and inside scattering media, respectively. The actual system latencies, defined as the time constants in the exponential relationship between the measured PBR and the speckle correlation time [23], were obtained by the experiments described in Section 3, and they were 3.0 ms and 6.0 ms for focusing light through and inside scattering media, respectively. It should be noted that by under-sampling speckle grains on Camera1 and the SLM [50], the number of optical degrees of freedom controlled by our system reached 2.6 × 10⁵, limited by the SLM pixel count (512 × 512 pixels). Our number of optical degrees of freedom is two to three orders of magnitude more than that in feedback and transmission matrix based wavefront shaping [5,7–9] and conventional adaptive optics experiments [51].

Fig. 3.

Workflow of TRUE optical focusing inside scattering media. A rolling shutter was used for Camera1, that is, neighboring rows are exposed successively with a 9.17 μs delay in the start times. The shutter for S (LS6, Vincent Associates) has a full-aperture transfer time of 0.8 ms, while the shutters for R_r (VSR14, Vincent Associates) and R_p (VS14, Vincent Associates) have full-aperture transfer times of 1.5 ms, because of larger aperture sizes (14 mm). FG, function generator; Ch, channel; RF, radio-frequency.

3. RESULTS

A. DOPC Performance Quantification

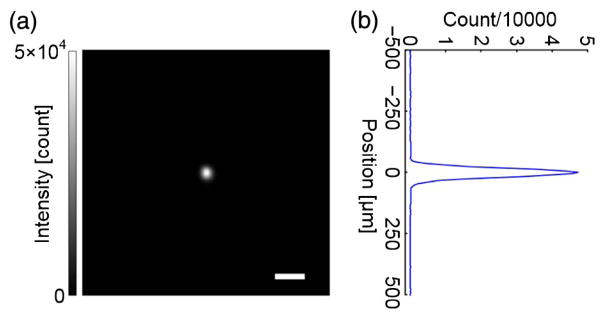
Similar to what was performed in Ref. [23], we quantified the performance of our system by calculating the ratio between the experimental and the theoretical PBR of the focus achieved by focusing light through an opal diffuser with a 4π scattering angle (10DIFF-VIS, Newport). PBR was calculated by the ratio between the average intensity of the pixels in the focus whose intensities are above half the maximum intensity and the ensemble average of the mean intensity of the speckles when a random wavefront was applied. Figure 4(a) shows the focus our DOPC system achieved when focusing light through the opal diffuser, and Fig. 4(b) shows the focal intensity distribution along the vertical direction. The experimental PBR is 5.1 × 10³, and the background intensity is calculated over an area of 1.2 × 1.2 mm. The theoretical PBR is calculated by N/(2πM), where N is the number of optical degrees of freedom, M is the number of speckle grains in the DOPC focus, and the factor of 2 is because that the opal diffuser nearly completely scrambles the polarization and our system phase conjugates only a single polarization of the sample light [52] (see Supplement 1). The speckle size on the FLC-SLM was 7.6 μm, computed from the full width at half-maximum (FWHM) of the autocovariance function of the speckle patterns measured by a camera with a pixel size of 3.45 μm. Since the camera lens for Camera1 had a magnification ratio of 0.43, the speckle size on Camera1 was 3.3 μm, which was smaller than the pixel size of Camera1 (6.5 μm). We intentionally had Camera1 under-sample the speckle grains to increase the number of optical degrees of freedom controlled by our DOPC system [50], so N = 512 × 512. To compute M, we measured the area of the achieved focus on Camera2 (1.5 × 10³ μm) and the area of a speckle grain on Camera2 (8.1 × 10² μm, computed from the speckle size). So, M = 1.9, and the theoretical PBR is N/(2πM) = 2.2 × 10⁴. Thus, the experimental PBR is 23% of the theoretical PBR, and the discrepancy is probably due to imperfect alignment and imperfect correction for the curvatures of the reference beams and the SLM.

Fig. 4.

System performance quantification. (a) Image of the DOPC focus after light passed through an opal diffuser with a 4π scattering angle. The PBR is 5.1 × 10³. Scale bar, 100 μm. (b) Focal intensity distribution along the vertical direction.

B. Focusing Light Through Moving Scattering Tissue

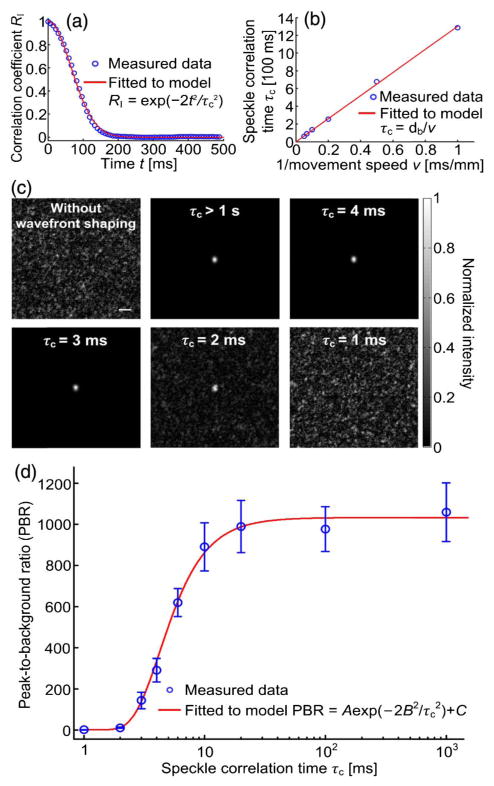
To measure the actual system latency, we used our DOPC system to focus light through a dynamic scattering medium with controllable speckle correlation times, achieved using a moving sample strategy [14,15,23,36,38,53–55]. The scattering sample was a 3 mm thick slice of fresh chicken breast tissue (scattering coefficient μ_s = 30 mm⁻¹, scattering anisotropy g = 0.965 [23]), sandwiched between two microscope slides. To ensure the tissue was 3 mm thick, three 1 mm thick microscope slides were used as spacers between the two microscope slides. To minimize the change of optical properties of the tissue, the sample chamber was sealed by aluminum foil tape to mitigate tissue dehydration, and all experiments were completed within 8 h of sample preparation. The sample was mounted on a linear stage with a motorized actuator (LTA-HS, Newport) to control the speckle correlation time on the SLM plane by controlling the tissue movement speed. To ensure the stage reached and maintained the preset speed, we started the wavefront measurement 10 s after the stage began to accelerate, and let the stage continue running for 10 s after the wavefront playback had finished (to avoid deceleration of the stage during measurement).

To measure the speckle correlation time at a given tissue movement speed, we used a camera with a pixel size of 3.45 μm to record movies of speckle patterns (along the horizontal polarization direction, by adding a polarizer) on the SLM plane as the tissue was moved. We could not use Camera1 for this task because the speckle grains were under-sampled on Camera1. Then, we calculated the correlation coefficients between the first and each of the ensuing frames of the recorded speckle patterns. By fitting the correlation coefficient R_I versus time, using $R_{\mathrm{I}}(t)=exp(-2t^2/{\tau }_{\mathrm{c}}^2)$ [15,54,56], we obtained the speckle correlation time τ_c, defined as the time during which the correlation coefficient decreases to 1/e² (= 13.5%) at a given tissue movement speed. As an example, Fig. 5(a) shows the correlation coefficient as a function of time when the tissue was moved at 0.01 mm/s, from which τ_c = 131 ms was determined. The relationship between the measured speckle correlation time τ_c and the preset tissue movement speed v is shown in Fig. 5(b). By fitting the experimental data with a theoretical model τ_c = d_b/v [15], we obtained τ_c = 1.3/v [ms] (the unit of v is mm/s), where d _b = 1.3 μm is the expected speckle size back-projected from the SLM plane to the sample plane through collection lens L5. Based on this equation, we were able to control the speckle correlation time by controlling the tissue movement speed.

Fig. 5.

Focusing light through moving scattering tissue. (a) Correlation coefficient between the speckle patterns as a function of time, when a 3 mm thick slice of chicken tissue was moved at 0.01 mm/s. Speckle correlation time τ_c =1.3 × 10² ms was determined for this speed. (b) Relationship between the speckle correlation time and the tissue movement speed. Errors bars are not plotted due to indiscernible lengths in the figure. (c) Images of the DOPC foci after light passed through the tissue, when the tissue was moved at different speeds. Scale bar, 100 μm. (d) PBR as a function of the speckle correlation time. The error bar shows the standard deviation of three measurements.

Figure 5(c) shows images of the DOPC foci recorded by Camera2 after light passed through the moving tissue when the corresponding speckle correlation time was varied from 1 ms to greater than 1 s (corresponding to zero movement speed). The representative binary-phase maps displayed on the SLM to achieve DOPC are shown in Supplement 1. A high-contrast focus was achieved when the speckle correlation time τ_c was no shorter than 2 ms. The PBRs for τ_c > 1 s, = 4 ms, = 3 ms, and = 2 ms are 1076, 271, 166, and 12, respectively. As a control, when a random phase map was displayed on the SLM, no focus was observed. When τ_c = 1 ms, we could not observe a focus because the DOPC system was not fast enough. As the PBR is proportional to the speckle correlation coefficient R_I (see Supplement 1 for a proof, also see [21]), the experimental PBR as a function of the speckle correlation time τ_c, shown in Fig. 5(d), can be fit by a theoretical model $\text{PBR}=Aexp(-2B^2/{\tau }_{\mathrm{c}}^2)+C$ (see Supplement 1). From the fit, we obtain the time constant B = 3.0 ms, which is the actual system latency [23]. When τ_c = B, the PBR reduces to ~1/e² of the PBR achieved when the sample is static.

C. Focusing Light Inside Moving Scattering Tissue

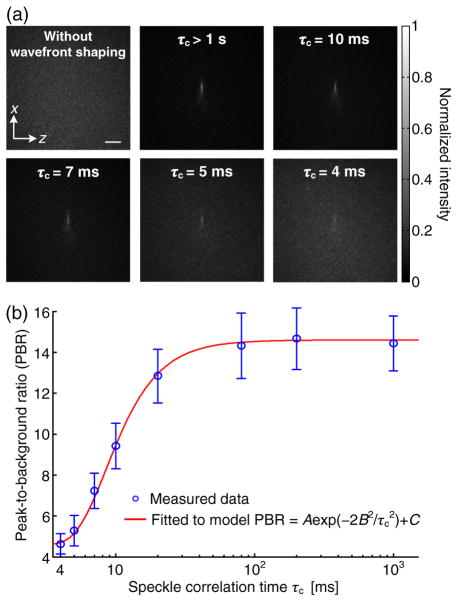
To quantify the actual system latency for focusing light inside scattering media, we used our DOPC system to focus light inside a dynamic scattering medium comprised of two pieces of chicken breast tissue, each 20 × 25 × 1 mm along the x, y, and z directions [see Fig. 2(e) for the orientations of the axes]. The second piece of tissue (the one between the ultrasonic focus and the SLM) was moved at different speeds by a motorized stage to control the speckle correlation time observed on the phase conjugate mirror. Following the same procedure as described in the preceding section, we calibrated the relationship between the speckle correlation time and the tissue movement speed and obtained τ_c = 1.5/v[ms] (the unit of v is mm/s). The illumination light intensity on the first piece of tissue was 6.6 × 10² mW/cm², which was 2.3 times higher than the safety limit from the American National Standards Institute. However, no apparent damage was observed in the tissue. Figure 6(a) shows the Camera2 recorded images of the foci achieved by TRUE focusing at speckle correlation times ranging from 4 ms to longer than 1 s (corresponding to zero movement speed). The representative binary-phase maps displayed on the SLM to achieve TRUE focusing are shown in Supplement 1. The FWHM focal spot size along the z direction was 62 μm, which is a little larger than the measured acoustic focal spot size along the transverse direction (47 μm). The FWHM focal spot size along the x direction (the acoustic axis direction) was 311 μm, which is close to the measured depth of focus of the acoustic focal zone (336 μm). The PBR of the focus decreases with decreasing speckle correlation time. As a control, when a random phase map was displayed on the SLM, no focus was observed. In Supplement 1, we mathematically prove that for a speckle field, such as the case in TRUE focusing, the PBR is still proportional to the speckle correlation coefficient R_I. Thus, the experimental PBR as a function of the speckle correlation time τ_c, shown in Fig. 6(b), can again be fit by the theoretical model $\text{PBR}=Aexp(-2B^2/{\tau }_{\mathrm{c}}^2)+C$. From the fit, we obtain the time constant B = 6.0 ms, which is the actual system latency for focusing light inside scattering media.

Fig. 6.

Focusing light inside a dynamic scattering medium comprised of two pieces of chicken tissue. (a) Images of the foci achieved by TRUE focusing at different speckle correlation times (τ_c). Scale bar, 500 μm. (b) The PBR as a function of the speckle correlation time. The error bar shows the standard deviation of three measurements.

4. DISCUSSION AND CONCLUSIONS

Currently, the speed bottleneck of our DOPC system is the low camera frame rate during wavefront measurement. Cameras with faster readout and data transfer will reduce the system runtime. Here, we used a camera exposure time of 0.5 ms, which is the minimum for this camera. By using a camera such as pco. edge 4.2, we can reduce the exposure time to 0.1 ms while roughly maintaining the frame rate. This change can reduce the system runtime by ~0.4 ms. For TRUE focusing, since the signal is often buried in a large background, it is ideal to use a lock-in camera to digitize only the signal after rejecting the background [24,54,57]. We have used a commercial lock-in camera to measure the wavefront in TRUE focusing within 0.3 ms, but the data transfer of this camera takes longer than 10 ms, limited by the low data transfer speed of USB 2.0 [24]. To achieve better performance, the pixel count of the lock-in camera needs to be increased (currently there are 300 × 300 pixels), and the data transfer rate needs to be improved by using a faster interface.

Because of the spontaneous electric polarization, ferroelectric liquid crystals respond to an external electric field much faster than nematic liquid crystals. Although the FLC molecules in the SLM we use have a response time of ~0.45 ms, FLC molecules with a much shorter response time (e.g., 0.04 ms) are available in other commercial FLC-SLMs (e.g., from Forth Dimension Displays). However, since these SLMs are mainly developed for display applications that do not require a speed as high as DOPC does, the net speed (< = 240 Hz) is currently limited by the data transfer speed of the display interface and needs to be increased. Also, for these FLC-SLMs, the image transfer protocol that is designed for transferring 24-bit RGB images needs to be modified to enable high-speed transfer of a binary image.

To obtain the phase map in TRUE focusing, our double exposure binary wavefront measurement method dramatically reduces the phase computation load compared with the traditional phase-shifting holography method [25,26], since our approach needs only to compare two numbers to get the binary-phase for each pixel, without the need to calculate the four-quadrant inverse tangent.

Since the speckle correlation time is inversely proportional to the tissue movement speed [15,54], in our experiments, we moved the tissue at different speeds to control the speckle correlation time observed on the phase conjugate mirror. This moving sample strategy has been used in previous works [14,15,23,36,38,53–55]; however, it cannot be excluded that the decorrelation caused by a moving scattering medium is subtly different from the decorrelation caused by living biological tissue or other dynamic scattering media such as fog and turbid water.

The speckle size in Figs. 5(c) and 6(a) is larger than half the optical wavelength, which can be explained as follows. During phase conjugation, the wavefront-shaped light was focused by lens L5 to a small spot on the surface of the sample. As a result, the diffused spot at the other side of the sample also had a small diameter, which enlarged the speckles at a distance from the sample.

In this work, we focused light inside a scattering medium comprising two pieces of tissue, with a beamsplitter placed between the two pieces to create a copy of the TRUE optical focus outside the water tank, so that the focus can be measured by a camera [Fig. 2(e)]. This configuration enables us to directly see the TRUE optical focus while the scattering medium decorrelates at different rates [Fig. 6(a)]. If there is no space between the two pieces of tissue, it would be extremely difficult to monitor the quality of TRUE focusing while the tissue is being moved at different speeds. Our system can be directly used for focusing light inside tissue, without modifying the software or hardware. The system runtime would be the same for focusing light inside tissue and focusing light in between two pieces of tissue. The only difference is that the PBR of the focus would be much lower when focusing light inside tissue, compared with when focusing light in between two pieces of tissue, because the speckle size inside tissue is much smaller than that between two pieces of tissue. When focusing light inside tissue, this small-speckle-size-induced low PBR is a major challenge to all acoustic-wave-guided wavefront shaping techniques [4,15,19,24–31,41,47,58–60]. This low PBR is a separate problem to solve that is beyond the scope of this work, which concentrates on improving the speed, rather than improving the PBR of TRUE focusing. In our study, the experimental PBR is approximately two orders of magnitude lower than the expected PBR, probably due to the low signal-to-noise ratio of TRUE focusing, imperfect corrections for the curvatures of the SLM and the reference beams, and imperfect alignment of the system. Because the theoretical PBR for focusing light inside thick tissue with 1064 nm light is slightly above 1, the experimental PBR would be low when focusing light inside tissue. To improve the PBR without sacrificing the speed by shrinking the light-sound interaction zone, we can use a long-coherence-length pulsed laser and a single-cycle ultrasound pulse [25,26]; we can also use an ultrasonic transducer with a higher central frequency and numerical aperture, at the cost of reducing the penetration depth. The methods developed in this work to improve the speed of TRUE focusing can be directly combined with the aforementioned two approaches to improve the PBR when focusing light inside tissue without sacrificing the speed. With the help of a long-coherence-length pulsed laser and a single-cycle ultrasound pulse, Ref. [25] has demonstrated TRUE optical focusing inside tissue. We may also increase the PBR by increasing the pixel count of the phase conjugate mirror, at the cost of reducing the system speed, or performing iterative TRUE focusing [28–30], while making sure to complete each iteration within the speckle correlation time.

In conclusion, we developed a high-speed DOPC system using a ferroelectric liquid crystal based SLM that achieves binary-phase modulation. Compared with DMDs that perform binary-amplitude modulation, FLC-SLMs double the PBR, have a higher malfunction threshold for pulsed lasers, and simplify the alignment of a DOPC system (because FLC-SLMs do not have oblique reflection angles as DMDs do). To take full advantage of the FLC-SLM and improve the speed of TRUE focusing, we developed a double-exposure binary wavefront measurement method. Our system focuses light through and inside scattering media, with system latencies of 3.0 ms and 6.0 ms, respectively. Since the demonstrated speed approaches tissue decorrelation rates, this work is an important step toward in vivo deep-tissue non-invasive optical imaging, manipulation, and therapy.