Probing topology by “heating”: Quantized circular dichroism in ultracold atoms

Physicists demonstrate how heating a quantum system can be used as a universal probe for exotic states of matter.

Abstract

We reveal an intriguing manifestation of topology, which appears in the depletion rate of topological states of matter in response to an external drive. This phenomenon is presented by analyzing the response of a generic two-dimensional (2D) Chern insulator subjected to a circular time-periodic perturbation. Because of the system’s chiral nature, the depletion rate is shown to depend on the orientation of the circular shake; taking the difference between the rates obtained from two opposite orientations of the drive, and integrating over a proper drive-frequency range, provides a direct measure of the topological Chern number (ν) of the populated band: This “differential integrated rate” is directly related to the strength of the driving field through the quantized coefficient η₀ = ν/ℏ², where h = 2π ℏ is Planck’s constant. Contrary to the integer quantum Hall effect, this quantized response is found to be nonlinear with respect to the strength of the driving field, and it explicitly involves interband transitions. We investigate the possibility of probing this phenomenon in ultracold gases and highlight the crucial role played by edge states in this effect. We extend our results to 3D lattices, establishing a link between depletion rates and the nonlinear photogalvanic effect predicted for Weyl semimetals. The quantized circular dichroism revealed in this work designates depletion rate measurements as a universal probe for topological order in quantum matter.

INTRODUCTION

The quantization of physical observables plays a central role in our understanding and appreciation of nature’s laws, as was already evidenced by the antique work of Pythagoras on harmonic series and, many centuries later, by the identification of the Balmer series in atomic physics (1). More recently, in condensed matter physics, the observation of quantized conductance unambiguously demonstrated the quantum nature of matter, in particular, the possibility for electronic currents to flow according to a finite set of conducting channels (2, 3). Although the quantized plateaus depicted by the conductance of mesoscopic channels depend on the samples geometry (3), a more universal behavior exists when a two-dimensional (2D) electron gas is immersed in an intense magnetic field (2): In the noninteracting regime, the Hall conductivity is then quantized according to the Thouless-Kohmoto-Nightingale-Nijs (TKNN) formula (4), σ_H = (e²/h)ν, where h is Planck’s constant, e is the elementary charge, and ν is a topological invariant—the Chern number—associated with the filled Bloch bands (5, 6). Since the discovery of this integer quantum Hall (QH) effect, the intimate connection between topology and quantized responses has been widely explored in solid-state physics (7–9), revealing remarkable effects such as the quantization of Faraday rotation in 3D topological insulators (10).

Building on their universal nature, topological properties are currently studied in an even broader context (11), ranging from ultracold atomic gases (12) and photonics (13, 14) to mechanical systems (15). These complementary and versatile platforms offer the possibility of revealing unique topological properties, such as those emanating from engineered dissipation (16–18), time-periodic modulations (19–27), quantum walks (28, 29), and controllable interactions (12, 30, 31). In ultracold gases, the equivalent of the TKNN formula was explored by visualizing the transverse displacement of an atomic cloud in response to an applied force (25); the Chern number ν and the underlying Berry curvature (9) were also extracted through state tomography (32, 33), interferometry (34), and spin polarization measurements (35). Besides, the propagation of robust chiral edge modes was identified in a variety of physical platforms (11–15).

Here, we demonstrate that the depletion rate of a Bloch band in a quantum lattice system, which reflects the interband (dissipative) response to a time-dependent perturbation, satisfies a quantization law imposed by topological properties. This observation of depletion rate quantization suggests that heating a system can be exploited to extract its topological order. Specifically, our method builds on the chiral nature of systems featuring Bloch bands with nonzero Chern number (7, 8). First, we find that the depletion rate of a circularly shaken Chern insulator, as captured by Fermi’s golden rule (FGR), crucially depends on the orientation (chirality) of the drive (Fig. 1). Then, we identify an intriguing quantization law for the differential integrated rate (DIR), ΔΓ^int, which is defined as the difference between the rates obtained from opposite orientations of the drive, integrated over a relevant frequency range. The quantization of the DIR can be simply expressed as

$${\mathrm{\Delta }\mathrm{\Gamma }}^{\text{int}}/{\mathit{A}}_{\text{syst}}={\mathrm{\eta }}_0{\mathit{E}}^2, {\mathrm{\eta }}_0=(1/{\mathrm{\hslash }}^2)\mathrm{\nu }$$ (1)

in terms of the drive amplitude E and the topological response coefficient η₀; here, ν denotes the Chern number of the populated band and A_syst is the system’s area. This result agrees with the intuition that the response of a trivial insulator (ν = 0) to a circular drive should not depend on the latter’s orientation. The quantized response (Eq. 1) identified in this work is nonlinear with respect to the strength of the driving field E, and it explicitly involves interband transitions (36), indicating that this phenomenon is distinct in essence from the TKNN paradigm (4), which is associated with linear transport and captured by single-band semiclassics (9, 37). This quantized effect related to circular dichroism establishes depletion rate measurements as a versatile probe for topological order.

Fig. 1. Topology through heating.

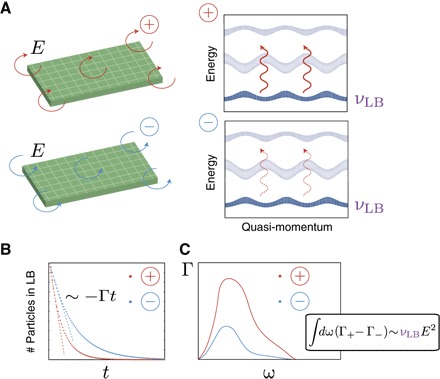
(A) A 2D Fermi gas is initially prepared in the lowest band (LB) of a lattice, with Chern number ν_LB, and it is then subjected to a circular time-periodic modulation (Eq. 3). (B) The rate Γ associated with the depletion of the populated band is found to depend on the orientation of the drive, Γ₊ ≠ Γ₋, whenever the LB is characterized by a nontrivial Chern number ν_LB ≠ 0. (C) Integrating the differential rate over a relevant drive-frequency range, ΔΓ^int = ∫dω(Γ₊ − Γ₋)/2, leads to a quantized result, ΔΓ^int/A_syst = (ν_LB/ℏ²)E², where E is the strength of the drive and A_syst is the system’s area (Eq. 1).

In the following, we demonstrate how the depletion rate that is associated with circularly driven Chern insulators can be related to the topological Chern number ν, and we identify the relevant response coefficient in this context, η₀ = ν/ℏ². We explain how this result relates to the general concept of circular dichroism through the universal Kramers-Kronig relations (38). We then discuss how this effect could be probed in realistic cold-atom systems, setting the focus on how to avoid the detrimental contribution of edge states in this framework. We then extend our results to 3D lattices, providing an instructive connection between topological depletion rates and the nonlinear photogalvanic effect (39) recently predicted for Weyl semimetals (40). Finally, concluding remarks and perspectives are presented.

RESULTS

Topology and quantization of integrated depletion rates

We start by studying a noninteracting (spinless) gas in a generic 2D lattice, as described by the single-particle Hamiltonian ${\widehat{\mathit{H}}}_0$. Here, we will assume that the lowest Bloch band (LB) of the spectrum, which is separated from higher bands by a bulk gap, Δ_gap, is initially completely filled with fermions; the following discussion can be straightforwardly extended to other initial filling conditions. Considering systems with broken time-reversal symmetry, the topological properties of this LB will be accurately captured by the Chern number (5–8), henceforth denoted as ν_LB. Thus, subjecting this system to a constant electric field E = E_y1_y generates a total Hall current J = J^x1_x satisfying the TKNN formula (4)

$${\mathit{J}}^{\mathit{x}}/{\mathit{A}}_{\text{syst}}={\mathit{j}}^{\mathit{x}}={\mathrm{\sigma }}_{\mathrm{H}}{\mathit{E}}_{\mathit{y}}, {\mathrm{\sigma }}_{\mathrm{H}}=({\mathit{q}}^2/\mathit{h}){\mathrm{\nu }}_{\text{LB}}$$ (2)

where A_syst is the system’s area and q is the charge of the carriers (q = e in an electron gas). In gases of neutral atoms, these transport equations can be probed by measuring the flow of particles (37, 41–43) in response to a synthetic electric field [for example, an optical gradient (25)]; this latter situation corresponds to setting q = 1 in Eq. 2.

Here, however, we are interested in the depletion rate of this system in response to a circular time-periodic perturbation, as described by the total time-dependent Hamiltonian

$${\widehat{\mathit{H}}}_{\pm }(\mathit{t})={\widehat{\mathit{H}}}_0+2\mathit{E}[\text{cos}(\mathrm{\omega }\mathit{t})\widehat{\mathit{x}}\pm \text{sin}(\mathrm{\omega }\mathit{t})\widehat{\mathit{y}}]$$ (3)

where ± refers to the two possible orientations (chirality) of the drive, $\widehat{\mathit{x}}$ and $\widehat{\mathit{y}}$ are the position operators (44), and ω is a frequency used to drive interband transitions. This circular shaking of 2D lattices can be implemented in cold atoms trapped in optical lattices (45) using piezoelectric actuators (24); the Hamiltonian in Eq. 3 equally describes electronic systems subjected to circularly polarized light (40, 46–49). The total number of particles scattered and extracted from the LB, N_±(ω, t) ≈ Γ_±(ω)t, is associated with the depletion rate Γ_± (Fig. 1), which can be accurately evaluated using FGR (50)

$${\mathrm{\Gamma }}_{\pm }(\mathrm{\omega })=\frac{2\mathrm{\pi }}{\mathrm{\hslash }}{\mathit{E}}^2{\displaystyle \sum _{\mathit{e}\notin \text{LB}}}{\displaystyle \sum _{\mathit{g}\in \text{LB}}}{|\langle \mathit{e}|\widehat{\mathit{x}}\pm \mathit{i}\widehat{\mathit{y}}|\mathit{g}\rangle |}^2{\mathrm{\delta }}^{(\mathit{t})}({\mathrm{\epsilon }}_{\mathit{e}}-{\mathrm{\epsilon }}_{\mathit{g}}-\mathrm{\hslash }\mathrm{\omega })$$ (4)

where |g〉 (resp. |e〉) denotes all the initially occupied (resp. unoccupied) single-particle states with energy ε_g (resp. ε_e) and δ^(t) (ε) = (2ℏ/πt) × sin²(εt/2ℏ)/ε²→δ(ε) in the long-time limit (51). The transitions to initially occupied states (g) are excluded in Eq. 4, as required by Fermi statistics, which is an important feature when many bands are initially occupied. We also point out that the number of scattered particles N_±(ω, t) can be directly detected in cold atoms by measuring the dynamical repopulation of the bands through band-mapping techniques, as was demonstrated for nontrivial Chern bands by Aidelsburger et al. (25).

For the sake of pedagogy, let us first analyze the excitation rate (Eq. 4) in a frame where the total Hamiltonian (Eq. 3) is translationally invariant. Performing the frame transformation generated by the operator

$${\widehat{\mathit{R}}}_{\pm }= \text{exp}\{\mathit{i}\frac{2\mathit{E}}{\mathrm{\hslash }\mathrm{\omega }}[\text{sin}(\mathrm{\omega }\mathit{t})\widehat{\mathit{x}}\mp \text{cos}(\mathrm{\omega }\mathit{t})\widehat{\mathit{y}}]\}$$ (5)

the time-dependent Hamiltonian (Eq. 3) is modified according to

$${\widehat{\mathcal{H}}}_{\pm }(\mathit{t})\approx {\widehat{\mathit{H}}}_0(\mathit{k})+\frac{2\mathit{E}}{\mathrm{\hslash }\mathrm{\omega }}\{\text{sin}(\mathrm{\omega }\mathit{t})\frac{\partial {\widehat{\mathit{H}}}_0(\mathit{k})}{\partial {\mathit{k}}_{\mathit{x}}}\mp \text{cos}(\mathrm{\omega }\mathit{t})\frac{\partial {\widehat{\mathit{H}}}_0(\mathit{k})}{\partial {\mathit{k}}_{\mathit{y}}}\}$$ (6)

where we now adopted the momentum (k) representation and omitted higher-order terms in E, in agreement with the perturbative approach (50) inherent to the FGR in Eq. 4 and below. In this frame, the depletion rate (Eq. 4) now takes the more suggestive form

$$\begin{array}{c}{\mathrm{\Gamma }}_{\pm }(\mathrm{\omega })={\displaystyle \sum _{\mathit{k}}}{\mathrm{\Gamma }}_{\pm }(\mathit{k};\mathrm{\omega })\\ {\mathrm{\Gamma }}_{\pm }(\mathit{k};\mathrm{\omega })=\frac{2\mathrm{\pi }}{\mathrm{\hslash }}{\displaystyle \sum _{\mathit{n}>0}}{|{\mathcal{V}}_{\mathit{n}0}^{\pm }(\mathit{k})|}^2{\mathrm{\delta }}^{(\mathit{t})}({\mathrm{\epsilon }}_{\mathit{n}}(\mathit{k})-{\mathrm{\epsilon }}_0(\mathit{k})-\mathrm{\hslash }\mathrm{\omega })\\ {|{\mathcal{V}}_{\mathit{n}0}^{\pm }(\mathit{k})|}^2={(\mathit{E}/\mathrm{\hslash }\mathrm{\omega })}^2{|\langle \mathit{n}(\mathit{k})|\frac{1}{\mathit{i}}\frac{\partial {\widehat{\mathit{H}}}_0}{\partial {\mathit{k}}_{\mathit{x}}}\mp \frac{\partial {\widehat{\mathit{H}}}_0}{\partial {\mathit{k}}_{\mathit{y}}}|0(\mathit{k})\rangle |}^2\end{array}$$ (7)

Here, we introduced the initially populated Bloch states of the LB, |g〉 ≡ |0(k)〉, of dispersion ε₀(k), as well as the initially unoccupied Bloch states of the higher bands, |e〉 ≡ |n(k)〉, of dispersion ε_n(k) and band index n. We note that, in an ideal, translationally invariant noninteracting system, the interband transitions occurring at each k yield Rabi oscillations (50), hence leading to a linear growth of the depletion rates Γ_±(k; ω); we point out that this effect, which is naturally damped in solid-state systems through disorder (40), is irrelevant when integrating the depletion rates over the drive frequency, as we now discuss.

Integrating the depletion rates Γ_±(ω) in Eq. 7 over all drive frequencies ω ≥ Δ_gap/ℏ, that is, activating all possible transitions between the filled LB and the higher bands (52), and considering the difference between these integrated rates, $\mathrm{\Delta }{\mathrm{\Gamma }}^{\text{int}}=({\mathrm{\Gamma }}_{+}^{\text{int}}-{\mathrm{\Gamma }}_{-}^{\text{int}})/2$, define the DIR, which reads

$${\mathrm{\Delta }\mathrm{\Gamma }}^{\text{int}}=4\mathrm{\pi }{(\mathit{E}/\mathrm{\hslash })}^2 \text{Im}{\displaystyle \sum _{\mathit{n}>0}}{\displaystyle \sum _{\mathit{k}}}\frac{\langle 0|{\partial }_{{\mathit{k}}_{\mathit{x}}}{\widehat{\mathit{H}}}_0|\mathit{n}\rangle \langle \mathit{n}|{\partial }_{{\mathit{k}}_{\mathit{y}}}{\widehat{\mathit{H}}}_0|0\rangle }{{({\mathrm{\epsilon }}_0-{\mathrm{\epsilon }}_{\mathit{n}})}^2}$$ (8)

Comparing the latter with the expression for the Chern number (9)

$${\mathit{v}}_{\text{LB}}=\frac{4\mathrm{\pi }}{{\mathit{A}}_{\text{syst}}}\text{Im}{\displaystyle \sum _{\mathit{n}>0}}{\displaystyle \sum _{\mathit{k}}}\frac{\langle 0|{\partial }_{{\mathit{k}}_{\mathit{x}}}{\widehat{\mathit{H}}}_0|\mathit{n}\rangle \langle \mathit{n}|{\partial }_{{\mathit{k}}_{\mathit{y}}}{\widehat{\mathit{H}}}_0|0\rangle }{{({\mathrm{\epsilon }}_0-{\mathrm{\epsilon }}_{\mathit{n}})}^2}$$ (9)

we obtain the simple quantization law for the DIR per unit area in Eq. 1, with ν = ν_LB.

Remarkably, the integration inherent to the definition of the DIR reveals the Chern number of the ground band, whereas the properties of excited states drop out through the summation over all final states. The relation in Eq. 1 is reminiscent of the transport equation (Eq. 2) associated with the QH effect: The DIR per unit area is directly related to the driving field E through a response coefficient η₀ that only depends on the topology of the populated band and on a universal constant (ℏ^{− 2}). We point out that, contrary to the linear transport equation (Eq. 2), the quantized response in Eq. 1 is nonlinear with respect to the driving field, which highlights its distinct origin. In particular, the differential aspect of the measurement, which directly probes the chirality of the system by comparing its response to the two opposite shaking orientations, plays an essential role in this distinct quantized effect. Besides, we note that the latter explicitly involves interband transitions, ruling out the possibility of capturing it through a single-band semiclassical approach (9). It is straightforward to generalize the result in Eq. 1 to situations where many bands are initially populated, in which case, ν_LB should be replaced by the sum over the Chern numbers associated with these bands.

In the case of two-band models (n = 1), we point out that the local differential rate ΔΓ(k; ω) = [Γ₊(k; ω) − Γ₋(k; ω)]/2 resulting from Eq. 7 is directly proportional to the Berry curvature Ω(k) of the LB (9). Hence, measuring ΔΓ(k; ω) from wave packets (prepared in the LB and centered around k) offers an elegant method to directly probe the geometrical properties of Bloch bands, as captured by the local Berry curvature (9). In addition, in that case, the allowed transitions are automatically restricted to |0(k)〉 → |1(k)〉, irrespective of Fermi statistics.

Practically, we propose that the integrated rates could be experimentally extracted from many individual depletion rate measurements (25, 52), corresponding to sampled (fixed) values of ω: ${\mathrm{\Gamma }}_{\pm }^{\text{int}}\approx {\sum }_{\mathit{l}}{\mathrm{\Gamma }}_{\pm }({\mathrm{\omega }}_{\mathit{l}}){\mathrm{\Delta }}_{\mathrm{\omega }}$, where the ω_l’s denote the many sampled frequencies separated by Δ_ω. This scheme could also be facilitated by the use of multifrequency drives [see the study of Schüler and Werner (53) for a very recent application of our scheme based on short pulses].

We have validated the quantization law in Eq. 1, on the basis of a numerical study of the two-band Haldane model (54), in the topological phase where ν_LB = − 1. The matrix elements, ${\mathcal{W}}_{\pm }=(2\mathrm{\pi }/\mathrm{\hslash })|{\mathcal{V}}_{10}^{\pm }(\mathit{k})|{}^2$, as defined in Eq. 7, were calculated for a honeycomb lattice of size 100 × 100, with periodic boundary conditions (PBC) (see Fig. 2). We verified that the DIR (Eq. 8), as evaluated from this numerical data and the density of states, yields ΔΓ^int(ℏ²/A_systE²) ≈ − 1.00, in perfect agreement with the quantized prediction of Eq. 1 (see also the Supplementary Materials).

Fig. 2. Transition matrix elements for the driven two-band Haldane model with 10⁴ lattice sites and PBC.

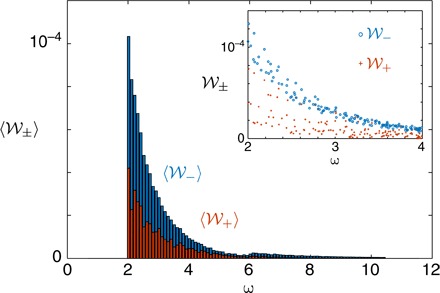
Specifically, the inset shows the matrix elements ${\mathcal{W}}_{\pm }=(2\mathrm{\pi }/\mathrm{\hslash }){|{\mathcal{V}}_{10}^{\pm }(\mathit{k})|}^2$, as defined in Eq. 7, for all possible transitions, ω = [ε₁(k) − ε₀(k)]/ℏ; the main plot shows the averaged values $\langle {\mathcal{W}}_{\pm }(\mathrm{\omega })\rangle$, defined within each interval of width Δ_ω = 0.1J/ℏ. The model parameters are set such that Δ_gap ≈ 2J, where J is the nearest-neighbor hopping amplitude; the strength of the drive (Eq. 3) is E = 0.001J/d, where d is the lattice spacing. The DIR (Eq. 8) obtained from this numerical data yields ΔΓ^int(ℏ²/A_systE²) ≈ −1.00, in agreement with Eq. 1 and the theoretical prediction ν_LB = −1. The matrix elements ${\mathcal{W}}_{\pm }$ are expressed in units of J²/ℏ, whereas the frequency ω is given in units of J/ℏ.

Relation to circular dichroism and Kramers-Kronig relations

The result in Eq. 1 is deeply connected to the well-known Kramers-Kronig relations (38), which are a direct consequence of the causal nature of response functions (46, 55). Considering the conductivity tensor σ^ab, the Kramers-Kronig relations take the form (46)

$${\mathrm{\sigma }}_{\mathit{R}}^{\mathit{a}\mathit{b}}(\mathrm{\omega })=(2/\mathrm{\pi }){\displaystyle {\int }_0^{\infty }\frac{\tilde{\mathrm{\omega }}{\mathrm{\sigma }}_{\mathit{I}}^{\mathit{a}\mathit{b}}(\tilde{\mathrm{\omega }})}{{\tilde{\mathrm{\omega }}}^2-{\mathrm{\omega }}^2}\mathrm{d}\tilde{\mathrm{\omega }}}$$ (10)

where ${\mathrm{\sigma }}^{\mathit{a}\mathit{b}}={\mathrm{\sigma }}_{\mathit{R}}^{\mathit{a}\mathit{b}}+\mathit{i}{\mathrm{\sigma }}_{\mathit{I}}^{\mathit{a}\mathit{b}}$ has been separated into real and imaginary parts and a, b = (x, y). In the limit ω → 0, the relation (Eq. 10) yields the sum rule

$${\mathrm{\sigma }}_{\mathrm{H}}\equiv \underset{\mathrm{\omega }\to 0}{\text{lim}}{\mathrm{\sigma }}_{\mathit{R}}^{\mathit{x}\mathit{y}}(\mathrm{\omega })=(2/\mathrm{\pi }){\displaystyle {\int }_0^{\infty }{\tilde{\mathrm{\omega }}}^{-1}{\mathrm{\sigma }}_{\mathit{I}}^{\mathit{x}\mathit{y}}(\tilde{\mathrm{\omega }})\mathrm{d}\tilde{\mathrm{\omega }}}$$ (11)

Besides, following Bennett and Stern (46), the power absorbed by a system subjected to the circular time-dependent perturbation in Eq. 3 can be related to the conductivity tensor as

$${\mathit{P}}_{\pm }(\mathrm{\omega })=4{\mathit{A}}_{\text{syst}}{\mathit{E}}^2[{\mathrm{\sigma }}_{\mathit{R}}^{\mathit{x}\mathit{x}}(\mathrm{\omega })\pm {\mathrm{\sigma }}_{\mathit{I}}^{\mathit{x}\mathit{y}}(\mathrm{\omega })]$$ (12)

where ± again refers to the orientation of the drive. Relating the depletion rate to the absorbed power, Γ_±(ω) = P_±(ω)/ℏω, and introducing the differential rate, ΔΓ = (Γ₊ − Γ₋)/2, then yields the useful relation

$${\mathrm{\sigma }}_{\mathit{I}}^{\mathit{x}\mathit{y}}(\mathrm{\omega })=\mathrm{\hslash }\mathrm{\omega }\mathrm{\Delta }\mathrm{\Gamma }(\mathrm{\omega })/4{\mathit{A}}_{\text{syst}}{\mathit{E}}^2$$ (13)

Finally, inserting Eq. 13 into Eq. 11 allows one to directly relate the DIR to the Hall conductivity σ_H of the probed system

$${\mathrm{\Delta }\mathrm{\Gamma }}^{\text{int}}/{\mathit{A}}_{\text{syst}}=(1/{\mathit{A}}_{\text{syst}}){\displaystyle {\int }_0^{\infty }}\mathrm{\Delta }\mathrm{\Gamma }(\mathrm{\omega })\mathrm{d}\mathrm{\omega }=(2\mathrm{\pi }{\mathit{E}}^2/\mathrm{\hslash }){\mathrm{\sigma }}_{\mathrm{H}}$$ (14)

The general expression (Eq. 14) leads to the quantization law in Eq. 1, when considering the TKNN formula for the Hall conductivity σ_H of a Chern insulator (see Eq. 2). We note that other intriguing sum rules have been identified in the context of circular dichroism (56) and that these could be exploited to access useful ground-state properties (for example, the orbital magnetization of insulators).

On the effects of boundaries

The derivation leading to Eq. 1 implicitly assumed translational invariance and PBC (that is, a torus geometry); in particular, this result disregards the effects related to the presence of (chiral) edge states in finite lattices (7, 8). Here, we reveal the important contribution of edge states when considering more realistic systems with boundaries.

To analyze lattices with edges [and more generally, systems that do not present translational symmetry, such as disordered systems (57) or quasi-crystals (58)], it is instructive to expand the modulus squared in the “real-space” formula (Eq. 4) and then to integrate the latter over all frequencies ω; this yields the integrated rates

$${\mathrm{\Gamma }}_{\pm }^{\text{int}}=(2\mathrm{\pi }/{\mathrm{\hslash }}^2){\mathit{E}}^2{\displaystyle \sum _{\mathit{g}\in \text{LB}}}\langle \mathit{g}|\widehat{\mathit{P}}(\widehat{\mathit{x}}\mp \mathit{i}\widehat{\mathit{y}})\widehat{\mathit{Q}}(\widehat{\mathit{x}}\pm \mathit{i}\widehat{\mathit{y}})\widehat{\mathit{P}}|\mathit{g}\rangle$$ (15)

where we introduced the projector $\widehat{\mathit{P}}=1-\widehat{\mathit{Q}}$ onto the LB. Thus, the expression for the DIR (Eq. 8) now takes the form

$$\begin{array}{c}{\mathrm{\Delta }\mathrm{\Gamma }}^{\text{int}}=({\mathrm{\Gamma }}_{+}^{\text{int}}-{\mathrm{\Gamma }}_{-}^{\text{int}})/2={(\mathit{E}/\mathrm{\hslash })}^2\text{Tr}\widehat{\mathrm{ℭ}}\\ \widehat{\mathrm{ℭ}}=4\mathrm{\pi } \text{Im} \widehat{\mathit{P}}\widehat{\mathit{x}}\widehat{\mathit{Q}}\widehat{\mathit{y}}\widehat{\mathit{P}}\end{array}$$ (16)

where Tr(⋅) is the trace. When applying PBC, the quantity $\left(\frac{1}{{\mathit{A}}_{\text{syst}}}\right)\text{Tr}\widehat{\mathfrak{C}}={\mathrm{\nu }}_{\text{LB}}$ is equal to the Chern number of the populated band (57, 59) such that the result in Eq. 1 is recovered in this real-space picture; in particular, this demonstrates the applicability of Eq. 1 to systems without translational symmetry.

The real-space approach allows for the identification of the strong edge-state contribution to the DIR ΔΓ^int, when (realistic) open boundary conditions (OBC) are considered. To see this, let us recall that the trace in Eq. 16 can be performed using the position (or Wannier state) basis {|r_j 〉}; in particular, inspired by Bianco and Resta (57) and Tran et al. (58), we decompose the DIR (Eq. 16) in terms of bulk and edge contributions

$${\mathrm{\Delta }\mathrm{\Gamma }}_{\text{OBC}}^{\text{int}}={(\mathit{E}/\mathrm{\hslash })}^2\{{\displaystyle \sum _{{\mathit{r}}_{\mathit{j}}\in \text{bulk}}}\mathit{C}({\mathit{r}}_{\mathit{j}})+{\displaystyle \sum _{{\mathit{r}}_{\mathit{j}}\in \text{edge}}}\mathit{C}({\mathit{r}}_{\mathit{j}})\}$$ (17)

where we introduced the local marker $\mathit{C}({\mathit{r}}_{\mathit{j}})=\langle {\mathit{r}}_{\mathit{j}}|\widehat{\mathrm{ℭ}}|{\mathit{r}}_{\mathit{j}}\rangle$. As illustrated in Fig. 3, the local marker C(r_j) ≈ ν_LB is almost perfectly uniform within the bulk of the system; in the thermodynamic limit, the bulk contribution $[{\sum }_{{\mathit{r}}_{\mathit{j}}\in \text{bulk}}\mathit{C}({\mathit{r}}_{\mathit{j}})\to {\mathit{A}}_{\text{syst}}{\mathrm{\nu }}_{\text{LB}}]$ leads to the quantized DIR predicted by Eq. 1 for PBC. However, the distinct contribution of the edge states, which is identified at the boundaries in Fig. 3, is found to exactly compensate the bulk contribution [see also the studies of Souza and Vanderbilt (56) and Bianco and Resta (57)]. Consequently, the total DIR in Eq. 17 vanishes for OBC, $\mathrm{\Delta }{\mathrm{\Gamma }}_{\text{OBC}}^{\text{int}}=0$, which agrees with the triviality of the underlying fiber bundle [the corresponding base space being flat (60)]. This important observation shows the marked role played by the boundary in the present context; in particular, it indicates that the edge-state contribution must be annihilated to observe the quantized DIR (Eq. 1) in experiments, as we further investigate in the paragraphs below.

Fig. 3. Local Chern marker C(r_j) in a 2D lattice with boundaries (OBC) realizing the Haldane model.

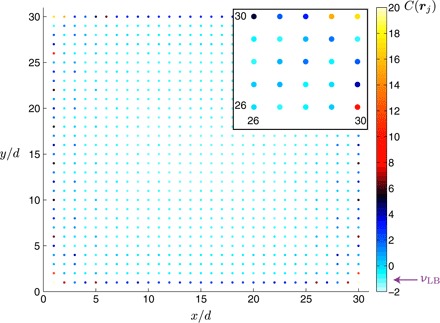
Far from the boundaries, the marker is C(r_j) ≈ −1, in agreement with the Chern number of the populated band ν_LB = −1. Close to the edges, the local marker is very large and positive (see the zoom shown in inset) such that the total contribution of the edges exactly cancels the bulk contribution, ${\sum }_{{\mathit{r}}_{\mathit{j}}}\mathit{C}({\mathit{r}}_{\mathit{j}})=0$: The DIR in Eq. 17 vanishes in a system with boundaries. Here, d is the lattice spacing.

Before doing so, let us emphasize that the detrimental contribution of the edge states cannot be simply avoided by performing a local measurement in the bulk, far from the edges. Probing the DIR in some region R would formally correspond to evaluating the quantity ${\mathrm{\mu }}_{\mathit{R}}=(1/{\mathit{A}}_{\text{syst}})\text{Tr}\tilde{\mathfrak{C}}$, where $\tilde{\mathfrak{C}}=4\mathrm{\pi }\text{Im}(\widehat{\mathit{P}}\widehat{\mathit{R}}\widehat{\mathit{x}}\widehat{\mathit{Q}}\widehat{\mathit{R}}\widehat{\mathit{y}}\widehat{\mathit{P}})$ and $\widehat{\mathit{R}}$ projects onto the region R. Although the local Chern number (57), defined as ${\mathrm{\nu }}_{\mathit{R}}=(4\mathrm{\pi }/{\mathit{A}}_{\text{syst}})\text{TrIm}(\widehat{\mathit{R}}\widehat{\mathit{P}}\widehat{\mathit{x}}\widehat{\mathit{Q}}\widehat{\mathit{y}}\widehat{\mathit{P}})\approx {\mathrm{\nu }}_{\text{LB}}$, can provide an approximate value for the Chern number of the LB, we find that μ_R strongly differs from this local marker ν_R because $[\widehat{\mathit{R}},\widehat{\mathit{P}}]\ne 0$.

Annihilating the edge-state contribution

We now introduce two protocols allowing for the annihilation of the undesired edge-state contribution. The first scheme consists of measuring the rate associated with the dynamical repopulation of the initially unoccupied bulk bands only, that is, disregarding the repopulation of edge states. In practice, this requires the knowledge of the bulk band structure. Formally, the resulting DIR would probe the quantity $\text{Tr}\widehat{\mathfrak{C}}$ in Eq. 16 but with the modified projector operator $\widehat{\mathit{Q}}\to {\widehat{\mathit{Q}}}_{\text{bulk}}$ that excludes the edge states of the spectrum. We have estimated the validity of this approach through a numerical study of the Haldane model with OBC and found that the topological marker ${\mathrm{\nu }}_{\text{bulk}}=(1/{\mathit{A}}_{\text{syst}})\text{Tr}{\widehat{\mathfrak{C}}}_{\text{bulk}}$ resulting from the modification $\widehat{\mathit{Q}}\to {\widehat{\mathit{Q}}}_{\text{bulk}}$ yields the approximate value ν_bulk ≈ −0.85 for a lattice with 2500 sites and ν_bulk ≈ −0.91 for a lattice with 10⁴ sites; these results, which are close to the ideal value ν_LB = −1, are found to be stable with respect to the Fermi energy (that is, to the number of initially populated edge states) and improve as the system size increases. We then validated this scheme through a complete numerical simulation of the full-time evolution associated with the circularly driven Haldane model with OBC: We found that the resulting response coefficient in Eq. 1 verified η₀ ≈ ν_bulk/ℏ², as estimated from the modified topological marker introduced above. This indicates how restricting the measurement of the depletion rate to the repopulation of bulk states only allows for a satisfactory evaluation of the quantized DIR in Eq. 1 under realistic conditions.

We then explore a more powerful scheme, which does not rely on the knowledge of the bulk band structure. Inspired by Dauphin and Goldman (61), we propose to initially prepare the system in the presence of a tight confining trap and then to release the latter before performing the heating protocol. In this case, edge states associated with the full (unconfined) lattice remain unpopulated because they do not couple to the time-evolving cloud upon the drive. We have validated this scheme numerically through a complete time evolution simulation of the circularly driven Haldane model, and we summarize the results in Fig. 4. Figure 4A shows the depletion rates Γ_±(ω_l), where the ω_l’s are the many sampled frequencies; here, features of the sinc-squared function are visible due to the finite observation time (Eq. 4). Figure 4B shows the value of the extracted Chern number ${\mathrm{\nu }}_{\text{LB}}^{\text{exp}}$ as a function of the frequency sampling step Δ_ω; these values were obtained by comparing Eq. 1 to the numerical DIR, ΔΓ^int = ∑_l[Γ₊(ω_l) − Γ₋(ω_l)]Δ_ω/2. In this protocol, a residual deviation from the ideal DIR quantization is still visible, even in the limit Δ_ω → 0 (see the saturation value ${\mathrm{\nu }}_{\text{LB}}^{\text{exp}}\approx -0.9$ in Fig. 4B). This is mainly due to the finite population of the higher band upon abruptly releasing the trap; we note that this weak effect is more pronounced for systems in which the Berry curvature is peaked close to the bandgap (for example, the Haldane model) and can be reduced by either increasing the initial size of the cloud or softening the release of the trap. This numerical study, based on a simulation of the full-time dynamics in real space, demonstrates the validity and robustness of this trap release protocol under reasonable experimental conditions, that is, an observation time of a few hopping periods and a limited number of sampled frequencies ω_l (see also fig. S1).

Fig. 4. Depletion rates for the trap-release protocol and the related Chern number measurement.

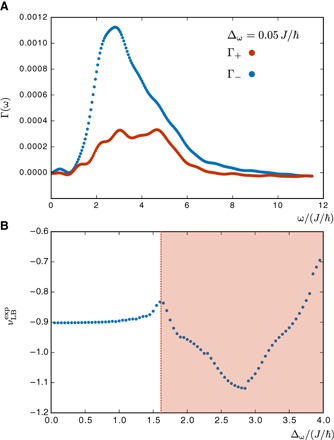
(A) Depletion rates Γ_±(ω) extracted from a numerical simulation of the circularly shaken Haldane model with OBC. The edge-state contribution has been annihilated by initially confining the cloud in a disc of radius r = 20d and then releasing it in a larger lattice of size 120 × 120, after which the heating protocol (circular drive) was applied; other system parameters are the same as in Fig. 2. The rates Γ_±(ω_l), which are expressed in units of J/ℏ, were obtained by measuring the number of excited particles after a time t = 4ℏ/J for fixed values of ω_l separated by Δ_ω = 0.05J/ℏ. (B) Approximate value for the Chern number of the populated band ${\mathrm{\nu }}_{\text{LB}}^{\text{exp}}$, as extracted from the numerical rates and Eq. 1, and represented as a function of the step Δ_ω used to sample the drive frequencies; note that the area A_syst entering Eq. 1 corresponds to the initial area of the cloud in the trap release protocol. A satisfactory measure is reached when the frequency sampling accurately probes the resonant peaks; we find Δ_ω ≲ 0.5J/ℏ (that is, at least 20 different values within the proper frequency range) for an observation time t = 4ℏ/J. The saturation value ${\mathrm{\nu }}_{\text{LB}}^{\text{exp}}\approx -0.9$ is limited by the fraction of particles populating the upper band, after abruptly removing the confinement, and can be improved by further increasing the initial radius r (or by softening the trap release).

We point out that the numerical results shown in Fig. 4 were obtained by initially confining the cloud using an infinitely abrupt circular trap, which can be designed in experiments (62). Besides, we stress that similar results would be obtained in more standard setups featuring smooth (harmonic) traps (63–65); in these configurations, the trap release protocol would then correspond to a significant change in the trap frequency [see the study of Dauphin and Goldman (61), where bulk topological responses were numerically investigated under this protocol].

Depletion rates and topology: Beyond 2D lattices

We now illustrate how differential depletion rates associated with a circular drive can probe topological matter in higher dimensions. We discuss two generic but distinct effects, which we concretely illustrate with Weyl semimetal Hamiltonians (66–70).

The first effect stems from a direct generalization of the 2D analysis; it relies on noting that the expression for ΔΓ^int given in Eq. 8 does not depend on dimensionality, provided that we consider spatial dimensions D > 1, where a chiral time modulation is well defined. In general, however, the sum over k in Eq. 8 involves a D-dimensional first Brillouin zone (FBZ), which leads to a nonquantized result. To see this, we generalize the drive operator in Eq. 3 as ${\widehat{\mathit{V}}}_{\pm }(\mathit{t})=\mathit{E}(\widehat{\mathit{a}}\pm \mathit{i}\widehat{\mathit{b}}){\mathit{e}}^{\mathit{i}\mathrm{\omega }\mathit{t}}+\mathrm{h}.\mathrm{c}.$, where $\widehat{\mathit{a}}\text{and}\widehat{\mathit{b}}$ are the position operators defining the polarization plane. Using these notations and considering the 3D case (D = 3), the DIR in Eq. 8 can be written as

$${\mathrm{\Delta }\mathrm{\Gamma }}^{\text{int}}/{\mathit{V}}_{\text{syst}}={\mathrm{\eta }}_{3\mathrm{D}}{\mathit{E}}^2, {\mathrm{\eta }}_{3\mathrm{D}}=\mathit{K}\cdot ({\mathbf{1}}_{\mathit{a}}\times {\mathbf{1}}_{\mathit{b}})/2\mathrm{\pi }{\mathrm{\hslash }}^2$$ (18)

where V_syst is the volume and K is a vector with units of momentum. As could have been anticipated from a 3D generalization of Eq. 14, the response coefficient η_3D is directly analogous to the general expression for the Hall conductivity in 3D, σ^ab = (e²/h)ϵ^abcK_c/2π, where K is known to contain information on the topology of the bands (71, 72). For instance, in the simplest case of a stacking of 2D Chern insulators, which is piled up along z with interplane separation d_z and is shaken by a circular drive polarized in the x-y plane, we find the DIR in Eq. 18 with K_z = 2πν_LB/d_z, where ν_LB is the Chern number associated with each plane. In the context of time-reversal-breaking Weyl semimetals, a similar calculation identifies K = ν_totd_W, where d_W is a vector connecting the Weyl nodes in k-space and ν_tot is the total Chern number of the occupied bands between these nodes (73–77). We recall that these Weyl semimetals can become 3D QH insulators whenever the Weyl nodes meet at the edge of the FBZ, in which case, the DIR in Eq. 18 is characterized by K = ν_totG⁰, where G⁰ is a primitive reciprocal lattice vector (72, 78). These results indicate that, similar to the Hall conductivity in 3D, the DIR in Eq. 18 can probe topological properties of the bands, as well as nonuniversal properties (for example, the Weyl node separation).

The considerations discussed above require a protocol involving an integration over frequencies (Eq. 8). Our second protocol only involves a single frequency ω and ultimately leads to a quantized signature stemming from the FGR in 3D lattices. It is based on a two-band analysis and builds on the observation that the differential current $\mathrm{\Delta }{\mathit{j}}^{\mathit{a}}=({\mathit{j}}_{+}^{\mathit{a}}-{\mathit{j}}_{-}^{\mathit{a}})/2$ is directly related to the local differential rate ΔΓ(k; ω) = [Γ₊(k; ω) − Γ₋(k; ω)]/2 (see Eq. 7) through

$$\frac{\mathit{d}\mathrm{\Delta }{\mathit{j}}^{\mathit{a}}}{\mathit{d}\mathit{t}}={\displaystyle {\int }_{\text{FBZ}}}\frac{{\mathrm{d}}^3\mathit{k}}{{(2\mathrm{\pi })}^3}({\mathrm{v}}_1^{\mathit{a}}-{\mathrm{v}}_0^{\mathit{a}})\mathrm{\Delta }\mathrm{\Gamma }(\mathit{k};\mathrm{\omega })$$ (19)

where ${\mathrm{v}}_{0,1}^{\mathit{a}}={\partial }_{{\mathit{k}}_{\mathit{a}}}[{\mathrm{\epsilon }}_{0,1}(\mathit{k})]$ are the band velocities in the two bands and where we set the charge q = 1. In this protocol, we take the polarization plane of the drive to be perpendicular to the direction a. Then, noting that the δ-function in ΔΓ(k; ω) (Eq. 7) defines a surface in k-space S orthogonal to the gradient ${\partial }_{{\mathit{k}}_{\mathit{a}}}({\mathrm{\epsilon }}_1-{\mathrm{\epsilon }}_0)$ leads to

$${\displaystyle \sum _{\mathit{a}=\mathit{x},\mathit{y},\mathit{z}}}\frac{\mathit{d}\mathrm{\Delta }{\mathit{j}}^{\mathit{a}}}{\mathit{d}\mathit{t}}=\frac{{\mathit{E}}^2}{8{\mathrm{\pi }}^2{\mathrm{\hslash }}^2}{\displaystyle {\int }_{\mathit{S}}}\mathrm{d}\mathbf{S}\cdot \mathbf{\Omega }=\frac{{\mathit{E}}^2}{4\mathrm{\pi }{\mathrm{\hslash }}^2}{\displaystyle \sum _{\mathit{i}}}{\mathit{C}}_{\mathit{i}}$$ (20)

where Ω denotes the Berry curvature vector (9) of the LB and where the last sum extends over all the momentum space monopoles i enclosed by the surface S with the integer charge C_i. If all monopoles in the FBZ lie inside S, then ∑_iC_i = 0. However, if S encloses an uneven number of positive and negative monopoles, for example, when Weyl nodes of opposite chirality lie at different energies, the quantity in Eq. 20 is nonzero and quantized. This result is an instance of the quantized nonlinear photogalvanic effect (39), predicted by de Juan et al. (40) for mirror-free Weyl semimetals; this alternative FGR derivation highlights the deep connection of this quantized phenomenon to the quantization law in Eq. 1. In particular, it suggests how this effect could be observed in a cold-atom realization of Weyl semimetals (79): If the band velocities ${\mathrm{v}}_{0,1}^{\mathit{a}}$ are known, measuring the local rate ΔΓ(k; ω) from wave packets can lead to a quantized measurement through the integration in Eq. 19. Alternatively, one could probe the current (43) or the related center-of-mass velocity (25, 37, 61), directly giving access to the left-hand side of Eq. 20. We note that similar Berry curvature effects have been recently investigated in the context of circular dichroism in nodal-line semimetals (80).

DISCUSSION

We demonstrated that the depletion rate of filled Bloch bands can satisfy a quantization law imposed by topology. This quantized effect positions depletion rate measurements as a powerful and universal probe for topological order in quantum matter. In this context, we emphasized the crucial necessity to isolate the bulk response from any detrimental effects associated with the edge modes, which, as we argued, can be realized by exploiting the highly controllable environment and tools offered by ultracold-atom setups.

Here, we illustrated this phenomenon by considering the case of 2D Chern insulators subjected to circular drives. However, we anticipate that other drive protocols could lead to distinct quantized responses in higher spatial dimensions D ≥ 3, offering the possibility of revealing other topological invariants [for example, higher-order Chern numbers (33, 81, 82)] through depletion rate measurements. We point out that a circular perturbation (Eq. 3) applied to a gapped surface of a 3D topological insulator (10) could reveal the half-integer QH effect, an unambiguous manifestation of these 3D topological states (7, 8, 83), through Eq. 14.

Moreover, we emphasize that the general result in Eq. 1 could be generalized to interacting systems, as suggested not only by the real-space approach (Eq. 16) but also by the general sum rule analysis leading to Eq. 14, which directly relates the DIR to the Hall conductivity of the probed system (and which does not make any assumption regarding the nature of interactions in the latter). In this sense, the quantized DIR introduced in this work could be exploited to probe the topological order [for example, the many-body Chern number (5)] of interacting systems, such as fractional Chern insulators (84). For instance, the DIR could directly reveal the fractional nature of the Hall conductivity, a striking signature of fractional Chern insulators (84), through Eq. 14. Finally, we note that similar schemes could also probe the chiral edge excitations of topological phases (63), as well as the spin chirality of strongly correlated states, as recently suggested by Kitamura et al. (85).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/8/e1701207/DC1

fig. S1. Depletion rates Γ_±(ω) as a function of the drive frequency ω for the driven two-band Haldane model with 10⁴ lattice sites and PBC.