Figure 5.

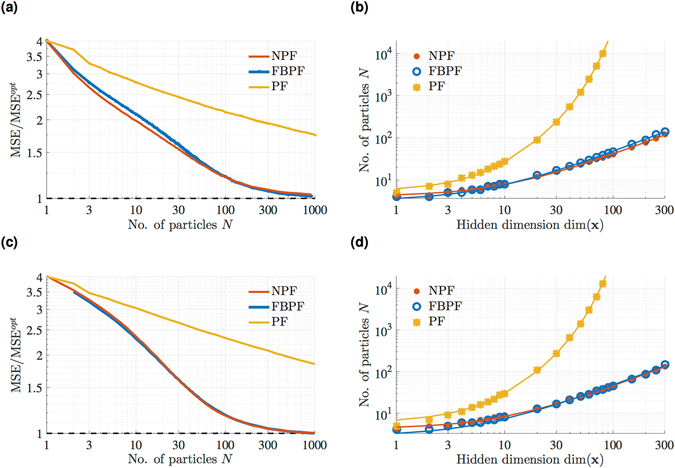
The NPF avoids the ‘curse of dimensionality’. (a) Filtering performance in terms of MSE (normalized to optimal performance, in this case $MS{E}^{\mathrm{o}\mathrm{p}\mathrm{t}}=0.5d$, where d denotes the number of hidden dimensions) for varying number of particles for a linear model with high-dimensional hidden state-space (d = 80). Both unweighted approaches NPF and FBPF outperform the (standard) weighted particle filter for a limited number of particles. (b) Number of particles needed to achieve a numerical performance $MSE<1.5MS{E}_{opt}$. The number of particles N needed for a standard (weighted) PF grows exponentially with d due to fast weight decay in higher dimensions. Contrarily, the unweighted approaches avoid the COD and the number of particles scales linearly with hidden dimensions. Solid lines correspond to linear ($N(d)=a\cdot d+b$, NPF: a = 0.38, b = 4.1 FBPF: a =0.45, b = 3.2) and exponential ($N(d)=c_0\cdot e^{c_{1}d}+c_2\cdot d+c_3$ PF: c ₀ = 47, c ₁ = 0.07, c ₂ = -2.4, c ₃ = -42) least-squares fits. (c,d) Same as (a,b), but for nonlinear hidden dynamics with a bimodal stationary distribution. Least-squares fit as coefficients: a = 0.42, b = 4.2 (NPF), a = 0.45, b = 2.8 (FBPF), c ₀ = 44, c ₁ = 0.07, c ₂ = -2.1, c ₃ = -38 (PF).