Significance
How do biological systems ensure robustness of function despite developmental and environmental variation? Although the operation of some systems appears to require precise control over parameter values, we describe how the function of the ear might instead be made robust to parameter perturbation. The sensory hair cells of the cochlea are physiologically vulnerable, yet most ears remain highly sensitive despite differences in their physical properties. We propose that slow homeostatic feedback allows hair cells to detect weak acoustic signals over a wide span of parameter values. Homeostasis also ensures that hair cells exhibit sharp frequency selectivity and a broad dynamic range. This homeostatic strategy constitutes a general principle by which many biological systems might ensure robustness of function.
Keywords: hair cell, hearing, nonlinear dynamics, oscillation, robustness
Abstract
Our sense of hearing boasts exquisite sensitivity, precise frequency discrimination, and a broad dynamic range. Experiments and modeling imply, however, that the auditory system achieves this performance for only a narrow range of parameter values. Small changes in these values could compromise hair cells’ ability to detect stimuli. We propose that, rather than exerting tight control over parameters, the auditory system uses a homeostatic mechanism that increases the robustness of its operation to variation in parameter values. To slowly adjust the response to sinusoidal stimulation, the homeostatic mechanism feeds back a rectified version of the hair bundle’s displacement to its adaptation process. When homeostasis is enforced, the range of parameter values for which the sensitivity, tuning sharpness, and dynamic range exceed specified thresholds can increase by more than an order of magnitude. Signatures in the hair cell’s behavior provide a means to determine through experiment whether such a mechanism operates in the auditory system. Robustness of function through homeostasis may be ensured in any system through mechanisms similar to those that we describe here.
Biological systems are subject to developmental variation and environmental fluctuations. Homeostatic mechanisms nonetheless ensure that most individuals function well under a variety of conditions. For example, homeotherms maintain an internal body temperature within a few degrees of a set point thanks to mechanisms such as sweating, panting, shivering, and redirecting blood flow. Many organisms regulate blood pressure by changing blood-vessel diameter or by adjusting heart rate or stroke volume. How homeostasis occurs remains an open question in many contexts, particularly when the system in question operates near a transition between two distinct behaviors, as has been suggested in gene expression, neuronal networks, and flocking (1–4). Here, we seek the general principles underlying homeostatic mechanisms by studying a specific system whose high level of performance derives from operating near a dynamical transition. We propose a strategy that increases the robustness of sensory transduction to parameter variation.
Within the range of human hearing, a trained ear can distinguish tones that differ in frequency by only 0.1% (5). The softest sounds that we can detect carry energies of the same magnitude as thermal fluctuations (6–9). We can, however, process sounds that convey a trillionfold more power (10). To achieve these specifications, the auditory system uses a set of active elements poised on the brink of self-oscillation (11). The presence of these self-oscillatory elements is evidenced by measurable sounds, termed spontaneous otoacoustic emissions, generated by our ears (8). It is unclear, however, how the auditory system maintains proximity to the boundary of spontaneous oscillation.
Within the cochlea, hair cells transduce sound-induced vibrations into electrical signals, which are subsequently communicated to the brain by afferent nerve fibers. Transduction is mediated by the mechanosensitive organelle of the hair cell, called the hair bundle. Positive deflection of the bundle opens ion channels, resulting in depolarization of the hair cell (Fig. 1A). Owing to an active process within hair cells, hair bundles can oscillate spontaneously (11, 12). This active process imparts to hair bundles enhanced sensitivity, improved frequency discrimination, and an extended dynamic range (13).
Fig. 1.
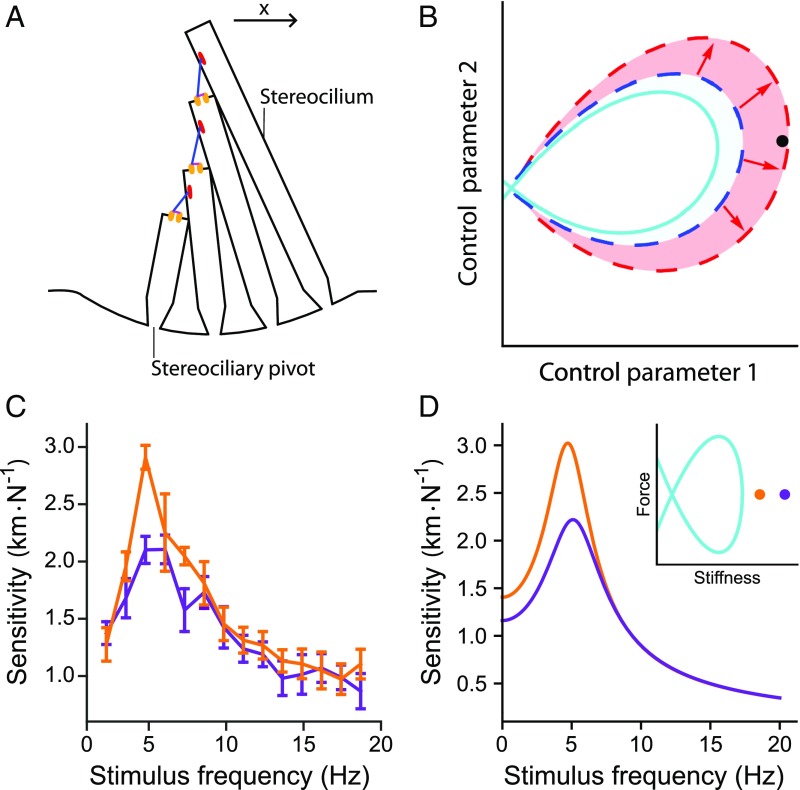
The sensitivity of a hair bundle to sinusoidal stimulation. () The hair bundle comprises a set of rigid, cylindrical stereocilia that protrude from the apical surface of the hair cell. Deflection of the hair bundle in the positive direction (arrow) pivots the stereocilia about their bases. This motion increases tension in tip links (blue) that run between neighboring stereocilia, which in turn opens mechanoelectrical transduction channels (orange). () A state diagram depicts the behavior of a hair bundle as a function of two control parameters. A line of Hopf bifurcations (solid, cyan) encircles the set of parameter values for which spontaneous oscillations occur. The entire shaded area marks the quiescent region in which the hair bundle possesses a sensitivity exceeding a specific threshold. The dashed curves mark the boundary of the high-performance region when the homeostatic mechanism is either inactive (blue) or active (red). At the black operating point, for example, the bundle’s sensitivity is poor when homeostasis is off, but above threshold when homeostasis is operational. () Tuning curves for an actual hair bundle from the bullfrog’s sacculus commanded to operate at stiffness values closer to (orange; 900 Nm-1) or farther from (purple; 1,000 Nm-1) the self-oscillation region. Sensitivity is defined to be the amplitude of the hair bundle’s phase-locked response at the stimulus frequency divided by the amplitude of the sinusoidal driving force. The control parameter is the bundle’s load stiffness, and this bundle traverses a Hopf bifurcation at 710 Nm-1 (SI Appendix, section 1). Error bars represent the standard errors of the means of four repeated measurements on the same hair bundle. Stimuli were delivered to the hair bundle directly by using a glass fiber (Materials and Methods and SI Appendix, section 1). () Sensitivity of a hair bundle model close to (orange; 750 Nm-1) or farther from (purple; 900 Nm-1) a Hopf bifurcation. D, Inset schematically depicts the model’s state diagram, whose axes are the size of a constant force applied to the bundle and the combined stiffness of the bundle and its overlying load; only positive stiffness values are represented. The Hopf bifurcation curve (cyan) encloses operating points at which the bundle oscillates spontaneously. These tuning curves were obtained from model II without homeostasis (Eqs. 4 and 5) with the parameter values listed in SI Appendix, Table S2, except m-1, m-1, , and pN. For this set of parameter values, a Hopf bifurcation occurs at a static deflection, or constant force, of 0 pN and a load stiffness of 248 Nm-1.
The simplest transition from quiescence to spontaneous oscillation as the value of a parameter is changed is known as a Hopf bifurcation. Near this transition, a system exhibits the three aforementioned properties desirable in a sound-detection apparatus: Amplification of small stimuli renders the system sensitive to weak sounds, sharp frequency selectivity promotes pitch discrimination, and a compressively nonlinear response enables the apparatus to process signals over a broad dynamic range (14–16). Each of these features, characteristic of our sense of hearing, has been observed in the vibrations of inner-ear structures (17). Furthermore, recent work has shown that individual hair bundles can operate close to a Hopf bifurcation (18, 19).
Since the concept was advanced, however, a major criticism of a Hopf bifurcation in hearing has been the precise parameter tuning necessary to reach the level of performance observed in our cochlea (14, 20–27). The auditory system’s ability to detect sound could be compromised by small changes in parameter values that move the system away from a Hopf bifurcation. In other words, the system’s function might not be robust to changes in parameter values. Acoustic trauma or pharmacological insults, which undoubtedly affect the system’s parameters, can indeed disrupt our hearing (28, 29). Nonetheless, our hearing ability is less vulnerable than our current understanding of the auditory system might suggest.
To visualize this problem, consider a hair bundle’s state diagram, which depicts the bundle’s behavior for different values of two control parameters (Fig. 1B). By changing the values of these parameters, we control the hair bundle’s operating point and thus the bundle’s behavior (18, 19, 30). The state diagram contains a line of Hopf bifurcations that encloses operating points at which the bundle oscillates spontaneously, whereas outside this curve the bundle is quiescent (SI Appendix, section 2). A mathematical model predicted this state-diagram structure, whose existence has been confirmed experimentally (18, 19, 30). The area surrounding the oscillatory region includes a set of operating points at which a quiescent bundle can attain a desired performance level. For example, the bundle’s sensitivity, defined as the system’s response to sinusoidal stimulation divided by the amplitude of the driving, exceeds a prescribed threshold in this region. This high-performance region may be very narrow, however, such that few operating points are included.
To illustrate how a hair bundle’s performance depends on its operating point, we experimentally determined sensitivity tuning curves for a hair bundle at two different operating points (Fig. 1C). In these experiments, the stiffness of the load applied to the bundle served as the control parameter. As the bundle was poised closer to self-oscillation, its peak sensitivity increased. This result accords with a model of hair bundle dynamics that possesses a state diagram with the same structure as that of actual hair bundles (Fig. 1D, Inset) (18, 19). Therefore, theory and experiment both show that a hair bundle is better able to detect sinusoidal signals if it operates closer to the brink of oscillating spontaneously.
We propose that a homeostatic mechanism increases the range of parameter values for which a bundle is sufficiently sensitive to periodic stimuli. This mechanism endows the system with a means of maintaining effective operation, which we term homeostasis of function. Homeostasis eases the demands on the system to precisely set its control parameter values, a strategy that we call robustness enhancement.
Results
Sensitivity.
Previous studies have shown that two features of a hair bundle, a nonlinear region of negative stiffness in the bundle’s force-displacement relationship and an active adaptation process, are sufficient to capture many aspects of bundle dynamics, including spontaneous oscillation (30). Negative stiffness is a passive consequence of channel gating, whereas adaptation pumps mechanical energy into the system to amplify the hair bundle’s response to stimulation.
To determine general principles associated with homeostasis of function, we introduce homeostatic mechanisms into two existing models of hair bundle motility. Model I possesses the simplest realizations of the hair bundle’s two essential features and exhibits dynamics that qualitatively agree with those of experimentally observed hair bundles (30). The simplicity of model I allows us to determine which elements of the model are sufficient to achieve robustness enhancement. Model II incorporates quantitative biophysical properties of the hair bundle (25). Adding homeostasis to model II allows us to determine which effects of homeostasis are generalizable from model I and to quantify the impact of homeostasis. Analyzing how these models differ in structure further facilitates our understanding of homeostatic mechanisms.
The homeostatic mechanisms in both models use a nonlinear term to rectify time-dependent changes in the hair bundle’s position. To minimize its effects on the dynamical response of the bundle to sinusoidal stimulation, the homeostatic mechanism operates slowly. Because experimental manipulations have been shown to affect adaptation, homeostatic feedback is applied to the models’ adaptation mechanisms, although other choices are possible (31–33). Additional motivation for the homeostatic mechanisms is provided in Discussion.
Model I with homeostasis is given by:
| [1] |
| [2] |
| [3] |
Here is the hair bundle’s displacement, is the combined stiffness of an external load and of the bundle , is a constant force applied to the bundle, and is an external force that varies in time. The overdots represent temporal derivatives. Negative stiffness appears in the bundle’s instantaneous force-displacement relation when , in which is a stiffness arising from channel gating (30). Eq. 2 describes the dynamics of adaptation , which produces a force on the bundle. The coefficient determines how strongly adaptation depends on bundle displacement, whereas the rate of the adaptation is set by (SI Appendix, section 2).
It has been shown that the mechanical load experienced by a hair bundle sets the bundle’s operating point and thus determines its biological function as a step detector, an oscillator, or a sinusoidal-signal detector (18, 19, 30). The parameters and control the bundle’s sensitivity to periodic stimulation (18, 19, 30). Our goal was to render the hair bundle’s ability to detect periodic stimuli more robust to changes in these control parameters. To achieve this objective, we took into account the dynamics of . Eq. 3 is termed the homeostatic mechanism because, as we will show, its inclusion imparts homeostasis of function upon the model. The timescale of the homeostatic mechanism is set by and gives the value to which would decay in the absence of homeostasis. Homeostasis is inactive when and active when (SI Appendix, section 3). Information about the hair bundle’s oscillation amplitude is captured by squaring the bundle’s displacement, imparting to the homeostasis equation a means of determining whether the bundle is receiving sinusoidal stimulation.
We evaluated the effects of the homeostatic mechanism on three measures, the first being sensitivity. The sensitivity of a system driven by a sinusoidal driving force is defined as the amplitude of the system’s phase-locked response at the driving frequency divided by the amplitude of the driving force : . Here and elsewhere, a tilde above a variable indicates the Fourier transform of that quantity. Larger sensitivity values indicate a lower input threshold for signal detection.
The sensitivity for weak stimulation is maximized when the system is driven at its resonant frequency (Fig. 1). The hair bundle’s peak sensitivity, , was calculated for operating points on the quiescent side of the Hopf bifurcation in the underdamped region of the state diagram (SI Appendix, sections 4 and 5). For quiescent bundles, the sensitivity is larger for operating points near the Hopf bifurcation. The peak sensitivity inside the region of spontaneous oscillation in the state diagram exceeds that in the quiescent region.
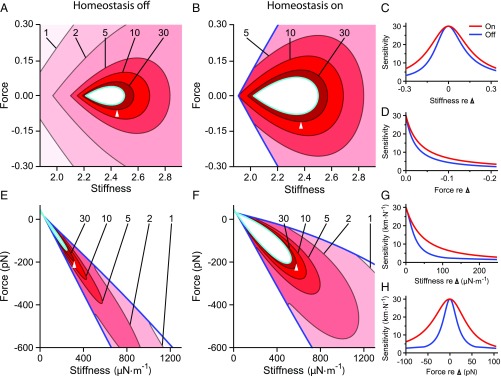
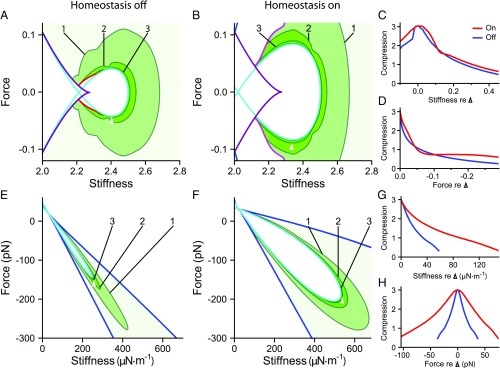
A hair bundle can detect a stimulus if the bundle’s response exceeds a threshold value. A curve of constant sensitivity encloses a region in the state diagram within which the bundle’s sensitivity exceeds some specified threshold. The larger this region, the more robust is signal detection to changes in the values of control parameters. Homeostasis dilates the area contained within each curve of constant peak sensitivity (Fig. 2A and B) and effects more gradual changes in sensitivity along lines of constant (Fig. 2C) or (Fig. 2D). Homeostasis through the adaptation rate thus renders the hair bundle’s sensitivity more robust to changes in the control parameters.
Fig. 2.
Homeostasis increases the robustness of a hair bundle’s sensitivity. ( and ) Sensitivity as a function of constant force and stiffness for model I when homeostasis is off () or on (). Darker shades of red indicate larger values of the peak sensitivity . Contours are labeled by their respective peak sensitivity values. The Hopf bifurcation curve is colored cyan, and the blue curve marks the boundary of the underdamped region. Homeostasis enhances the robustness of the hair bundle’s sensitivity to small-amplitude sinusoidal signals by expanding the areas enclosed by the sensitivity contours. ( and ) The peak sensitivities along a horizontal () or vertical () slice through the state diagram when homeostasis is inactive (blue) or active (red). These curves correspond to slices through the reference operating points indicated in and , respectively (apices of white triangles). The peak sensitivity is larger and changes more slowly along these transects when homeostasis is active. (E–H) The results for model II are portrayed as for A–D. The contour labels in and bear units of kmN-1. All parameter values are listed in SI Appendix, Tables S1 and S2. Additional bifurcation lines that occur in these regions of the state diagrams are not shown (SI Appendix, sections 8 and 9).
Model II with homeostasis is given by:
| [4] |
| [5] |
| [6] |
| [7] |
in which , , , and bear the same meanings as in model I. is the collective stiffness of the gating springs that connect mechanotransduction channels to bundle displacement. is the displacement of the hair bundle’s tip that results when a channel opens, and is the probability that a channel is open. The open probability is described by a Boltzmann function, Eq. 7, derived from a two-state channel model; controls the function’s position, and controls its width. Channel gating introduces into the system nonlinearity, the first essential ingredient, through the sigmoidal shape of (25).
The second vital ingredient, adaptation, is powered by a Ca2+ gradient and by myosin motors that exert forces to open the channels. The position of the motors serves as the adaptation variable , Eq. 5. The influx of Ca2+ through open channels inhibits the motors, resulting in channel reclosure. This arrangement constitutes an adaptation mechanism, because it allows the hair bundle to remain sensitive to farther deflection. determines the strength of Ca2+ inhibition. The extent spring possesses stiffness and equilibrium length . The drag coefficients and account for hydrodynamic damping.
Eq. 6 constitutes the homeostatic mechanism in model II and describes the dynamics of the myosin motor force . The form of Eq. 6 parallels that of Eq. 3: sets the timescale of the homeostatic process, decays to in the absence of homeostasis, and determines how strongly the current state of the system affects the homeostatic mechanism. Homeostasis is off when and operational when (SI Appendix, section 3). In contrast to Eq. 3, Eq. 6 uses a saturating nonlinearity: The bundle’s oscillation amplitude is measured by the sigmoidal function in Eq. 6. Eq. 6 has a physical interpretation: The motor force is set by the average Ca2+-concentration gradient across the hair cell’s plasma membrane, which is adjusted by the ion’s influx through the channels. Because homeostasis depends on the transduction current, could depend on the Ca2+-concentration gradient and on the membrane potential.
Curves of constant peak sensitivity in model II’s state diagram reveal that engaging the homeostatic mechanism augments the areas contained within each contour (Fig. 2 E and F and SI Appendix, section 4). Moreover, when evaluated along a line of constant stiffness (Fig. 2G) or force (Fig. 2H), the peak sensitivity changes more slowly when homeostasis is operational than when it is inactive. When homeostasis is active, the bundle can accommodate larger perturbations in the values of control parameters, while still maintaining its ability to detect small signals. Although model II takes into account the dynamics of the active force rather than the rate of adaptation , these results echo those found for model I.
Model I has a state diagram that is symmetric about the line . Because of the symmetric dependence of Eq. 3 on the bundle’s displacement, the symmetry present in model I’s state diagram is unaffected by the homeostatic mechanism. Homeostasis consequently changes the size but not the orientation of the contours. Model II lacks symmetry, owing to an asymmetry inherent to hair bundle physiology, namely the sigmoidal relation of the channel open probability to hair bundle displacement. Because Eq. 6 is not symmetric with respect to displacement, engaging the homeostatic mechanism in model II dilates, reshapes, and reorients the oscillatory region.
Frequency Selectivity.
We next examined how the hair bundle’s frequency selectivity is affected by the homeostatic mechanisms. The quality factor is defined as the system’s resonant frequency divided by the frequency bandwidth over which the oscillation power exceeds half the maximum at resonance: . Large values of indicate that a system is sharply tuned. Quality factors as large as 30 have been measured in the mammalian cochlea (17).
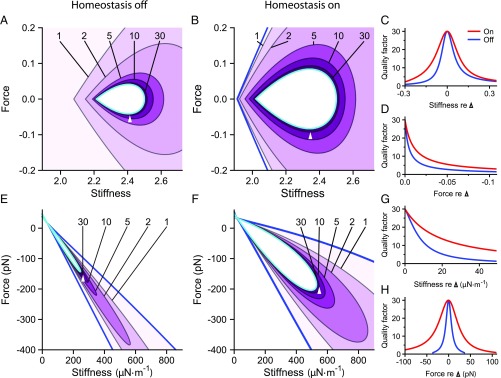
We delineate the quality factor contours within the quiescent, underdamped region of the hair bundle’s state diagram. Frequency tuning is sharper at operating points that are closer to the self-oscillation region (Fig. 3) and sharper still inside the oscillatory region. Endowing model I with its homeostatic mechanism renders more robust to changes in the values of the control parameters. When the homeostatic mechanism is engaged, contours enclose larger areas in the state diagram than when homeostasis is off (Fig. 3 A and B). Homeostasis also reduces the rate of change of along lines of constant stiffness or force (Fig. 3 C and D).
Fig. 3.
Homeostasis increases the robustness of a hair bundle’s frequency selectivity. ( and ) Contours of the quality factor are shown in the state diagram of model I for homeostasis off and homeostasis on (). Each contour is labeled with its respective value of , and darker shades of purple indicate larger values. ( and ) The quality factor along horizontal () or vertical () slices that pass through the reference operating points indicated in and (white triangle apices) when homeostasis is off (blue) or on (red). () The results for model II are portrayed as for . In each contour plot, the Hopf bifurcation curve is colored cyan, and the blue curve marks the boundary of the underdamped region of the state diagram. All parameter values are listed in SI Appendix, Tables S1 and S2, and the alignment of the curves in , , , and is as described in Fig. 2. Additional bifurcation lines that occur in these regions of the state diagrams are not shown (SI Appendix, sections 8 and 9).
For model II, the homeostatic mechanism enlarges the regions contained within contours (Fig. 3 E and F) and diminishes the steepness of ’s dependence on each control parameter (Fig. 3 G and H). The precision needed in selecting the hair bundle’s operating point to ensure sharp frequency selectivity is therefore reduced by the two distinct homeostatic mechanisms used in models I and II.
The quality factor increases monotonically with the length of time that a system requires to reach its steady state: Sharper frequency selectivity is obtained at the expense of a slowed response onset. By rendering more robust, the homeostatic mechanism in either model reduces the set of operating points at which the bundle can respond quickly to stimuli. Frequency discrimination is improved at the expense of temporal resolution. Owing to greater robustness enhancement, homeostasis causes larger proportional increases in response times in model II than in model I. Sharper frequency selectivity can be obtained, however, at a slightly lower cost in relaxation time for model II than for model I (SI Appendix, section 6).
Compressive Range.
A hair bundle can detect signals over a finite range of amplitudes, defined as the bundle’s dynamic range. If the amplitude of a system’s response to stimulation is proportional to the magnitude of stimulation , then the system’s dynamic range must be restricted by the range of permissible response amplitudes. A broader dynamic range can be attained if the system’s response amplitude grows more slowly with stimulus amplitude, compressing a wide range of inputs into a narrower range of outputs.
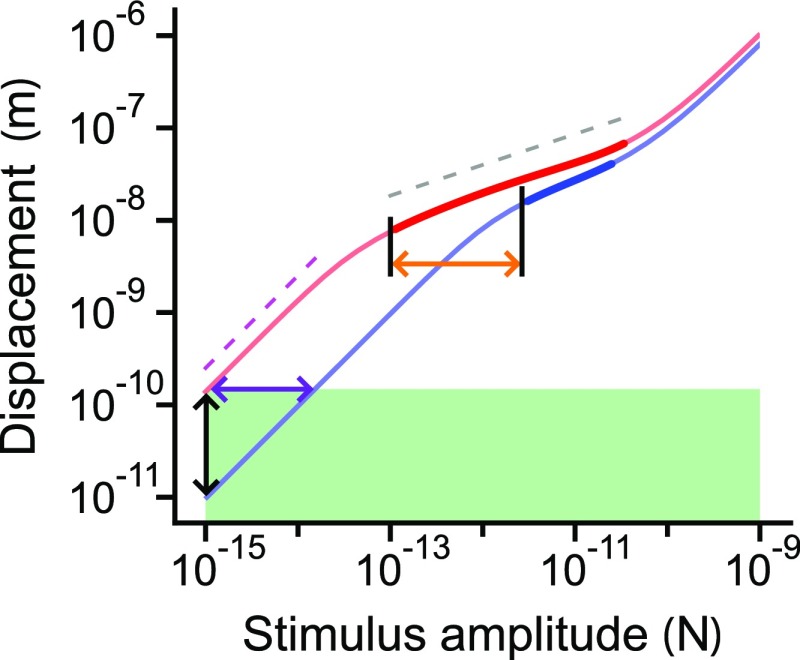
A system that operates at a Hopf bifurcation exhibits nonlinear compression that obeys the one-third power law (15). Such a system represents six orders of stimulus magnitude with only two orders of magnitude in the amplitude of the response. Near the bifurcation, nonlinear compression occurs for a limited range of stimulus amplitudes, termed the compressive range (Fig. 4). We define this range to be the span, in logarithmic units, of stimulus amplitudes over which the amplitude of the response grows according to , in which the exponent falls in the interval . This condition restricts our analysis to strong compression and avoids numerical complications (SI Appendix, section 7).
Fig. 4.
Increasing the compressive range broadens a bundle’s dynamic range. The responses of model II, absent homeostasis, to periodic stimulation at the resonant frequency are shown for operating points closer to (red) and farther from (blue) the self-oscillation region. The response , in which is the slope of the curves in the doubly logarithmic plot. Thin portions of the curves have slopes between 1/2 and 1, whereas thick portions bear slopes between 0 and 1/2. For comparison, the relations (dashed magenta line) and (dashed gray line) are shown. The horizontal span of the thick part of each curve defines that operating point’s compressive range. Points on the curves above the area shaded green exceed a threshold in displacement. The dynamic range of the red curve equals the width of the green rectangle; the dynamic range of the blue curve is smaller by one order of magnitude (purple arrow). This difference stems from the red curve’s larger compressive range (orange arrow). Extending the dynamic range renders the bundle more sensitive to low-amplitude stimuli (blackarrow).
Curves of constant compressive range for each model show that operating points close to the Hopf bifurcations in the state diagrams have a broad compressive range (Fig. 5). The homeostatic mechanism used in model I expands the range of parameter values over which the compressive range exceeds a threshold. Furthermore, the compressive range changes more slowly in size at most values of stiffness or constant force. For model II, the compressive-range contours encompass larger regions when homeostasis is active than when inactive (Fig. 5 E and F), and the slope of the bundle’s compressive range as a function of either stiffness or force is significantly less steep when homeostasis is operational (Fig. 5 G and H). Both homeostatic mechanisms succeed in rendering the bundle’s dynamic range more robust to changes in the control parameters.
Fig. 5.
Homeostasis increases the robustness of a hair bundle’s dynamic range. () A contour plot showing curves of constant compressive range for model I when homeostasis is off. ( and ) Compressive range is shown as a function of the stiffness (abscissa) and constant force (ordinate). The contour labels indicate the size of the compressive range in orders of magnitude of the periodic forcing amplitude; see Fig. 4 for examples. Darker shades of green indicate broader compressive ranges. The purple curve is a line of saddle-node bifurcations; saddle-node bifurcations of limit cycles are colored red. () A contour plot of compressive range when homeostasis is on. Multimodal oscillations occur in response to sinusoidal forcing within the region on the left-hand side of the magenta curves. The purple curve is a line of saddle-node bifurcations. The apices of the white triangles indicate the reference operating points through which horizontal and vertical slices are taken to generate the curves for and , respectively. (–) Compressive range for model II when homeostasis is inactive or active . and show the compressive range of the bundle along either a horizontal or vertical slice through the apices of the white triangles in and . The Hopf bifurcation curve is colored cyan in each contour plot, and the blue curve marks the boundary of the underdamped region of the state diagrams. At each operating point, sinusoidal stimuli are delivered at the bundle’s resonant frequency, which varies as a function of stiffness and constant force. The stimulus frequency is not changed to match possible shifts in the peak frequency as the forcing amplitude increases. The compressive range is not calculated within the white regions of state space. “Compression” signifies the compressive range in , , , and . Additional information about the excluded regions can be found in SI Appendix, section 8. All parameter values are listed in SI Appendix, Tables S1 and S2, and the alignment of the curves in , , , and is as described in Fig. 2. Additional bifurcation lines that occur in these regions of the state diagram are not shown (SI Appendix, sections 8 and 9).
Model I uses two nonsaturating nonlinearities: Eq. 1 bears a cubic term, and Eq. 3 is quadratic in the bundle’s displacement. A consequence of the first nonlinearity is the absence of an upper bound on the hair bundle’s compressive range. The second nonlinearity results in unbounded responses to very large forces when homeostasis is active (SI Appendix, section 7). Both of these issues are resolved in model II by using the saturating nonlinearity , which more closely approximates reality.
The saddle-node bifurcations, saddle-node bifurcations of limit cycles, and multimodal response boundaries shown in Fig. 5 were excluded from Figs. 2 and 3 for the sake of clarity; in these three figures, the diagrams contain the same set of bifurcations. The Hopf bifurcation curve comprises supercritical and subcritical parts (SI Appendix, section 8). The advantages and disadvantages of poising a bundle near the supercritical or subcritical portions of the Hopf bifurcation curve are discussed elsewhere (19).
Robustness Enhancement.
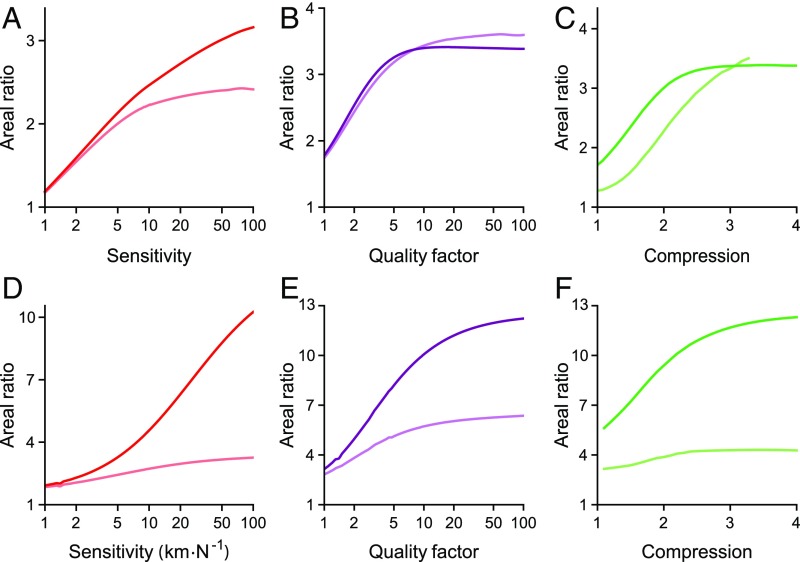
To quantify the degree of robustness enhancement, we calculated the areas contained within contours of peak sensitivity, sharp tuning, and compressive range. The ratio of the areas in the “homeostasis on” state diagram to those of the “homeostasis off” state diagram yielded a measure of robustness enhancement termed the areal ratio. The areal ratios for peak sensitivity, frequency tuning, and compressive range always exceed one and become greater for contours closer to the self-oscillation region (Fig. 6). The size of this effect can be increased by changing the parameters controlling homeostasis (SI Appendix, section 3). We conclude that both homeostatic strategies render the hair bundle’s ability to detect signals more robust to parameter variation, with the greatest enhancement occurring for operating points located close to the line of Hopf bifurcations.
Fig. 6.
Quantification of robustness enhancement. The values reported represent the ratios of areas enclosed by contours in the homeostasis on state diagrams to areas bounded by contours in the homeostasis off state diagrams. The oscillatory region of the state diagram is either included (darker) or excluded (lighter). – Areal ratios for model I: peak sensitivity (), quality factor , and compressive range . – Areal ratios for model II: peak sensitivity (), quality factor , and compressive range . The entire areas enclosed by some contours are not shown in Figs. 2, 3, and 5, but are included in our calculation of areal ratios.
It is unclear whether the self-oscillation region of the state diagram is used by hair bundles responsible for detecting sinusoidal signals. Including the area of self-oscillation mildly affects the enhancement for model I: Areal ratios are slightly greater than or comparable to values found when the self-oscillation region is excluded. In model II, however, including the regions of spontaneous oscillation yields much larger areal ratios, particularly for greater values of peak sensitivity, tuning sharpness, and compressive range (Fig. 6). When the self-oscillation regions are included, the areal ratios for both models approach the factor by which homeostasis dilates the size of the oscillatory region for large values of sensitivity, tuning sharpness, and compressive range. At small values of these measures, the oscillatory region makes only a small contribution to the area enclosed by the contours and therefore does not significantly affect the areal ratios.
Transient Responses.
We have shown that robustness enhancement can be effected through homeostatic mechanisms. However, it remains to be determined whether actual hair bundles use such a strategy. Obtaining direct evidence that homeostatic mechanisms improve the robustness of a bundle’s responsiveness is complicated by the challenging nature of experimentally mapping the bundle’s state diagram and by our ignorance of the homeostatic mechanism’s identity. We therefore describe additional consequences of homeostasis that are more amenable to experimental testing. Because homeostasis produces systems whose behavior is governed by an additional timescale, identifying hair bundle behaviors that betray the presence of such a timescale would provide support for the presence of homeostasis.
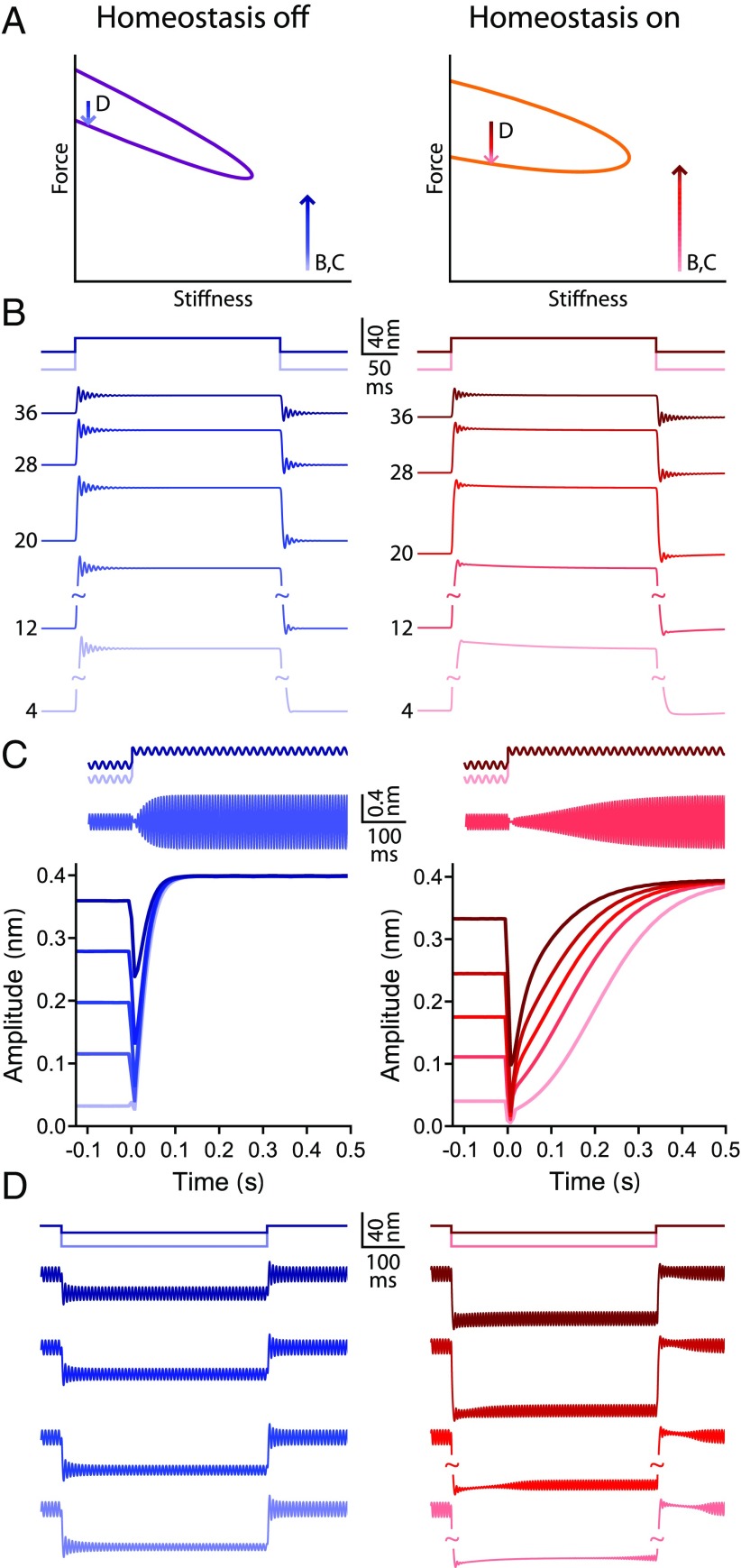
One approach is to ask how a bundle poised to operate within the quiescent, underdamped region of the state diagram responds to force steps (Fig. 7). A positive step is applied to shift the bundle from various initial operating points to the same reference operating point. An operating point at which the bundle has a peak sensitivity of 40 kmN-1 is chosen as the reference operating point in both the homeostasis off and on case. The relaxation time for small stimuli at the reference operating point is consequently similar with and without homeostasis. However, engaging the homeostatic mechanism alters the bundle’s response to large stimuli. At the onset of each force step, the bundle exhibits ringing, whose magnitude and duration are similar for all initial operating points when homeostasis is inactive (Fig. 7B). When homeostasis is turned on, the ringing behavior diminishes in amplitude and vanishes more quickly for initial operating points farther from the reference operating point. Homeostasis alters the relaxation dynamics associated with force steps.
Fig. 7.
Hair bundle behaviors associated with homeostasis. A schematic diagram showing the locations of the operating points and directions of the force steps used; labels indicate to which panel(s) each arrow applies. The Hopf bifurcation curve is colored purple when homeostasis is off (left) and orange when homeostasis is on (right). () The response to positive force steps for a bundle poised in the quiescent, underdamped region of the state diagram. Traces are labeled by the initial operating point’s peak sensitivity in kmN-1. All force steps bring the bundle to the same reference operating point (tip of B,C arrows in ), which has a peak sensitivity of 40 kmN-1. The peak sensitivity at the reference point is a maximum as a function of the constant force. The stimulation protocols for the largest and smallest steps are shown schematically above the traces. (B, Left) When homeostasis is off, the ringing after the onset of the force step is not appreciably affected by the initial operating point. (B, Right) When homeostasis is on, the size and duration of the ringing diminish as the distance between the initial and reference operating points increases. () Schematic protocol of the force steps with a superimposed sinusoidal driving force delivered to a bundle. The frequency of the sinusoidal component is equal to the bundle’s resonant frequency at the reference operating point (tip of B,C arrows in ), and the sinusoid’s amplitude is 0.01 pN. The bundle’s initial operating points and the size of the force steps are the same as in . Representative traces are shown when homeostasis is off (C, Left) or on (C, Right). (C, Left) When homeostasis is off, the bundle quickly reaches a steady state after the onset of the force step. (C, Right) When homeostasis is on, a greater interval is needed for the bundle to reach a steady state. () Response to negative force steps for a bundle poised in the self-oscillation region. Lighter shades of blue indicate larger step sizes. The schematic diagrams above the traces show the stimulation protocols for the largest and smallest force steps. The initial operating points for this protocol are chosen so that the bundle’s oscillation amplitude is 17 nm in the absence or presence of homeostasis. The bundle’s oscillation amplitude reaches a maximum as a function of the constant force at the initial operating points. The bundle’s operating point is contained within the self-oscillation region throughout the entire protocol (D arrow in ). (D, Left) When homeostasis is off, spontaneous oscillations are not interrupted by the force steps. (D, Right) When homeostasis is active, a delay precedes the return of spontaneous oscillations at the onset and offset of the force step, and this delay lengthens as the size of the force step increases. All simulations are generated by using model II, with parameter values listed in SI Appendix, Table S2.
A second stimulation protocol adds sinusoidal forcing to the force steps described above. The stimulus frequency is chosen to match the resonant frequency at the reference point. When homeostasis is turned off, the bundle’s oscillation amplitude quickly reaches a steady state, and the response time is not strongly affected by changing the initial operating point (Fig. 7C). In contrast, when homeostasis is active, the bundle requires more time to reach a steady state, and this time delay grows systematically as the distance between the reference and initial operating points increases. Homeostasis retards the response to periodic stimuli.
In a final paradigm, force steps are delivered to a spontaneously oscillating hair bundle. In this protocol, the bundle’s initial operating point is the common reference point, and the final operating point is varied. The bundle’s amplitude of spontaneous oscillation at the reference operating point is chosen to be the same for the homeostasis off and on cases. Negative force steps are applied to shift the bundle’s operating point closer to the edge of the oscillatory region. When homeostasis is inactive, spontaneous oscillations appear almost immediately after the onset and offset of the force step, regardless of the step’s size (Fig. 7D). In contrast, when homeostasis is active, the return of spontaneous oscillations is delayed. The delay lengthens as the size of the force step increases. Once again, homeostasis introduces a lag in the bundle’s dynamics.
Discussion
Any biological system must contend with a host of constraints. Failing to operate within these constraints hinders the system’s ability to function. In this work, we have demonstrated how a hair bundle could use homeostatic mechanisms to ease such constraints. Two homeostasis strategies, accounting for the dynamics of the adaptation rate or of the adaptation motor’s strength, enhance the robustness of the hair bundle’s sensitivity, frequency selectivity, and dynamic range to changes in parameter values. That these disparate homeostasis strategies produce qualitatively similar results suggests that enhancing robustness through homeostasis is a general principle. We conjecture that a homeostatic mechanism renders the bundle’s signal-detection function more robust to changes in all parameter values and that equipping other systems with homeostasis would yield similar effects. The values of the parameters in the homeostasis equations could well have evolved to preserve the robustness of the bundle’s function to changes in these parameter values (SI Appendix, section 3).
Although the two models we investigate differ in a number of ways, their common features underlie the generality of our results. In the absence of homeostasis, the models possess topologically similar state diagrams, each characterized by a region of spontaneous oscillation bounded by a line of Hopf bifurcations. Moreover, each model involves a homeostatic mechanism that decreases the value of a target variable in response to an increasing measured variable. We show that these elements are sufficient to ensure robustness of function for an active periodic-signal detector. A homeostatic mechanism with this structure together with a state diagram containing the aforementioned properties may constitute the minimal features needed to enhance a system’s robustness of function.
For each control parameter that we evaluated, homeostasis renders the bundle’s signal-detection ability more robust. The robustness enhancement is related to the factor by which the homeostatic mechanism dilates the size of the oscillatory region (SI Appendix, section 3). Identifying a homeostatic mechanism that enlarges the self-oscillation region likely constitutes a general strategy for enhancing the robustness of an oscillator’s function to changes in parameter values.
The forms of the homeostatic mechanisms are biologically plausible. Each uses information about the current state of the hair bundle; the homeostatic equation measures the bundle’s oscillation amplitude through the mechanotransduction current. This information is rectified by a nonlinearity of the homeostatic process, which ensures that the process responds when the bundle is stimulated by a sinusoidal force. In model I, we show that a quadratic nonlinearity is sufficient to provide rectification, whereas model II enacts rectification by using a biophysically motivated nonlinearity—namely, a Boltzmann function. The homeostatic mechanisms require few assumptions so that either could be realized through several biological processes. For example, both homeostatic mechanisms could be effected through myosin-motor inhibition mediated by a Ca2+-activated second messenger (34) or through regulation of Ca2+ buffers (35, 36) or pumps (35, 37).
The homeostatic mechanism operates on a timescale that greatly exceeds both the channels’ relaxation time of a few milliseconds and the adaptation time constant of tens of milliseconds (38, 39). This timescale separation ensures that the homeostatic mechanism does not perturb the system’s ability to detect periodic signals. When driven at the resonance frequency, the period of the bundle’s oscillation was shorter than 20 in model I or 20 ms in model II for the vast majority of operating points in the underdamped region. We chose and ms so that these timescales are long compared with those of bundle oscillation, in accord with the timescales of the potential homeostatic mechanisms mentioned above.
Temporal resolution is sacrificed to attain robustness of function in two ways. First, by extending the range of parameter values over which the bundle exhibits sharply tuned frequency selectivity, the homeostatic mechanism also broadens the set of operating points at which the bundle’s response is slow. This tradeoff poses a disadvantage only if a signal detector must strongly prioritize temporal resolution over frequency selectivity. Second, the bundle’s transient responses to sinusoidal stimulation reveal that the homeostatic mechanism engenders delays on the order of hundreds of milliseconds (Fig. 7). That these delays are long reflects our decision to use parameter values that accord with measurements and estimates in saccular hair cells of the bullfrog. These cells are tuned to frequencies of a few tens of hertz, and their sensory function does not demand that they respond quickly to sinusoidal stimuli. Were we to use instead parameter values drawn from measurements in mammalian hair cells that are tuned to higher frequencies, the delays would be shorter, and the homeostatic mechanism would not degrade the cells’ temporal resolution below that required for higher-frequency hearing. There is some evidence, however, that homeostatic feedback within our cochlea is quite slow (see below).
Our models resemble a model that neglects adaptation, but accounts for somatic motility, the change in length of an outer hair cell in response to a change in membrane potential (27). Feedback provided by somatic motility can engender spontaneous oscillations in cochlear models, yielding state diagrams similar to those discussed here. Enhancement of robustness through a homeostatic mechanism is not specific to models endowed with adaptation, but instead represents a principle that applies to models using many forms of feedback.
Two types of hair cells are present within the mammalian cochlea: Inner hair cells provide input to the brain, whereas outer hair cells amplify the vibrational response of the cochlea (40, 41). Feedback to the outer hair cells from efferent fibers originating in the medial olivocochlear nucleus could constitute a homeostatic mechanism similar to those that we describe (41). Stimulation of efferents innervating outer hair cells alters the cochlea’s mechanical response to acoustic stimulation, diminishing both sensitivity and dynamic range (40, 42). There is also evidence that efferent stimulation reduces the cochlea’s frequency selectivity (43, 44). Moreover, feedback through efferents occurs in 100 ms for fast effects and in tens of seconds for slow effects, timescales that are long compared with the response time of a few milliseconds for cochlear mechanics (42, 45). Because our models require only a resonant amplifier to which a homeostatic mechanism is added, they suggest how efferent-mediated homeostasis could enhance the robustness of cochlear function.
Noise diminishes a hair bundle’s sensitivity, frequency selectivity, and dynamic range (46). Homeostasis, through the feedback that it exerts, propagates stochastic fluctuations of the bundle’s position into the adaptation process. Accounting for noise may therefore decrease the degree of robustness enhancement. For sufficiently weak noise, the homeostatic mechanism should nonetheless improve the robustness of a bundle’s function to parameter variation.
Because bifurcations may be blurred or shifted by noise, it can be challenging to precisely locate them in noisy systems (47). In experiments, we address this difficulty by using a statistical test to delineate the boundary of a bundle’s self-oscillation regime (SI Appendix, section 1). Near the boundary, we predict that a hair bundle will take longer to relax after a constant force step when homeostasis is present than when it is absent.
Multiple timescales have been seen in the dynamics of hair bundle motion (31, 48). However, delays in a bundle’s return to spontaneous oscillations were reported to depend on the duration rather than on the magnitude of the force steps, possibly because large force steps were used (48). Here we have shown that a homeostatic mechanism introduces an additional timescale whose signatures might be observed in the bundle’s transient response (Fig. 7). Noise may make it difficult to see in experiments the bundle’s predicted transient responses to sinusoidal stimulation applied during force steps. The sizes of the force steps and amplitude of sinusoidal forcing can be adjusted, however, to maximize the predicted effects; we hope that a sufficiently large stimulus will evoke a behavior that is not obscured by noise. Alternatively, the long relaxation times owing to homeostasis may be evident only in the average over many stimulus trials. Evaluating transient responses in hair bundles or in cochlear vibrations evoked by the stimulation protocols described in this work might provide evidence for a homeostatic mechanism in hearing.
Owing to homeostatic feedback, bursting oscillations arise in our models for low values of stiffness. At these operating points, the timescale for homeostatic feedback is similar to the hair bundle’s period of spontaneous oscillation. Although these bursting oscillations can be entrained by sinusoidal forcing (31), the utility of multimodal responses in hearing remains uncertain.
In this work, we sought to achieve homeostasis of function—namely, of a system’s sensitivity, sharpness of tuning, and dynamic range. This strategy constitutes a conceptual departure from existing approaches that instead seek homeostasis of parameter values. Previous models have relied on a strong assumption: that the system’s behavior is not significantly altered by conferring dynamics on a control parameter (20–26, 49). We show that this assumption does not hold in general: Introducing homeostasis changes a system’s state diagram and its dynamics. Furthermore, our method does not require that the system maintain a representation of the set-point values to which parameters must be tuned.
The approach described in this work is general and likely applicable to any system whose function depends on oscillatory elements. A few examples drawn from biology include circadian clocks (50, 51), beating cardiomyocytes (52), and insulin–glucose oscillations (53). The functions of these systems depend on their ability to detect and entrain to periodic stimuli. Homeostatic mechanisms may ensure that the function of these systems is robust to developmental and environmental variation.
Materials and Methods
Experimental Protocols.
Detailed descriptions have been published of the tissue preparation, imaging apparatus, mechanical-load clamp, data acquisition, and time-series analysis (18, 19). In each experiment, the sensory epithelium from the sacculus of an adult American bullfrog, Rana catesbiana, was mounted into a two-compartment chamber. Using a rapid feedback system and piezoelectrical stimulator, we applied to an individual hair bundle the displacements and forces necessary to situate a mechanically active bundle at specific positions in its state diagram. In this way, we were able to determine the load stiffness or force value at which spontaneous oscillations were suppressed and, thus, to approximate the location of the Hopf bifurcation. The location of the bifurcation was subsequently confirmed by using Hartigans’ dip statistic (SI Appendix, section 1). After the hair bundle had been poised at an operating point on the quiescent side of the bifurcation, sinusoidal stimulation with an amplitude of 10 pN was delivered at a sequence of 14 evenly spaced driving frequencies from 2.3 to 18.7 Hz. The bundle was then commanded to an operating point with a larger load stiffness, at which the stimulus sequence was repeated. The procedure continued for several additional operating points farther from the Hopf bifurcation with multiple replicates obtained for each operating point. The resulting time series were analyzed in MATLAB (Version R2015a; MathWorks). The sensitivity of the hair bundle’s response to periodic forcing was calculated as the bundle’s phase-locked motion at the driving frequency divided by the amplitude of the stimulus at the driving frequency averaged over replications, and finally the magnitude of the resulting value was taken as:
Analytical Calculations and Simulations.
All analytical calculations and numerical simulations were performed by using Mathematica (Version 10.1; Wolfram). Further details are provided in SI Appendix.
Supplementary Material
Acknowledgments
We thank B. Fabella for his technical expertise and the members of our research group for comments on the manuscript. This work was supported by National Institutes of Health Grants F30DC015697 (to A.R.M.), F30DC013468 (to J.D.S.), and T32GM07739 (to A.R.M. and J.D.S.). A.J.H. is an Investigator of Howard Hughes Medical Institute.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1706242114/-/DCSupplemental.
References
- 1.Beggs JM, Plenz D. Neuronal avalanches in neocortical circuits. J Neurosci. 2003;23:11167–11177. doi: 10.1523/JNEUROSCI.23-35-11167.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nykter M, et al. Gene expression dynamics in the macrophage exhibit criticality. Proc Natl Acad Sci USA. 2008;105:1897–1900. doi: 10.1073/pnas.0711525105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Krotov D, Dubuis JO, Gregor T, Bialek W. Morphogenesis at criticality. Proc Natl Acad Sci USA. 2014;111:3683–3688. doi: 10.1073/pnas.1324186111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bialek W, et al. Statistical mechanics for natural flocks of birds. Proc Natl Acad Sci USA. 2012;109:4786–4791. doi: 10.1073/pnas.1118633109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Spiegel MF, Watson CS. Performance on frequency-discrimination tasks by musicians and nonmusicians. J Acoust Soc Am. 1984;76:1690–1695. [Google Scholar]
- 6.Sivian LJ, White SD. On minimum audible sound fields. J Acoust Soc Am. 1933;4:288–321. [Google Scholar]
- 7.de Vries HL. Brownian movement and hearing. Physica. 1948;14:48–60. [Google Scholar]
- 8.Harris GG. Brownian motion in the cochlear partition. J Acoust Soc Am. 1968;44:176–186. doi: 10.1121/1.1911052. [DOI] [PubMed] [Google Scholar]
- 9.Dalhoff E, Turcanu D, Zenner HP, Gummer AW. Distortion product otoacoustic emissions measured as vibration on the eardrum of human subjects. Proc Natl Acad Sci USA. 2007;104:1546–1551. doi: 10.1073/pnas.0610185103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Knudsen VO. The sensibility of the ear to small differences of intensity and frequency. Phys Rev. 1923;21:84–102. [Google Scholar]
- 11.Hudspeth AJ. Integrating the active process of hair cells with cochlear function. Nat Rev Neurosci. 2014;15:600–614. doi: 10.1038/nrn3786. [DOI] [PubMed] [Google Scholar]
- 12.Hudspeth AJ. Making an effort to listen: Mechanical amplification in the ear. Neuron. 2008;59:530–545. doi: 10.1016/j.neuron.2008.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Martin P, Hudspeth AJ. Compressive nonlinearity in the hair bundle’s active response to mechanical stimulation. Proc Natl Acad Sci USA. 2001;98:14386–14391. doi: 10.1073/pnas.251530498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Choe Y, Magnasco MO, Hudspeth AJ. A model for amplification of hair bundle motion by cyclical binding of Ca2+ to mechanoelectrical-transduction channels. Proc Natl Acad Sci USA. 1998;95:15321–15326. doi: 10.1073/pnas.95.26.15321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eguíluz VM, Ospeck M, Choe Y, Hudspeth AJ, Magnasco MO. Essential nonlinearities in hearing. Phys Rev Lett. 2000;84:5232–5235. doi: 10.1103/PhysRevLett.84.5232. [DOI] [PubMed] [Google Scholar]
- 16.Hudspeth AJ, Jülicher F, Martin P. A critique of the critical cochlea: Hopf–a bifurcation–Is better than none. J Neurophysiol. 2010;104:1219–1229. doi: 10.1152/jn.00437.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Salvi JD, Ó Maoiléidigh D, Fabella BA, Tobin M, Hudspeth AJ. Control of a hair bundle’s mechanosensory function by its mechanical load. Proc Natl Acad Sci USA. 2015;112:E1000–E1009. doi: 10.1073/pnas.1501453112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Salvi JD, Ó Maoiléidigh D, Hudspeth AJ. Identification of bifurcations from observations of noisy biological oscillators. Biophys J. 2016;111:798–812. doi: 10.1016/j.bpj.2016.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Camalet S, Duke T, Jülicher F, Prost J. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proc Natl Acad Sci USA. 2000;97:3183–3188. doi: 10.1073/pnas.97.7.3183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jülicher F. Mechanical oscillations at the cellular scale. C R Phys. 2001;2:849–860. [Google Scholar]
- 22.Vilfan A, Duke T. Two adaptation processes in auditory hair cells together can provide an active amplifier. Biophys J. 2003;85:191–203. doi: 10.1016/S0006-3495(03)74465-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Moreau L, Sontag E. Balancing at the border of instability. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;68:020901-1–020901-4. doi: 10.1103/PhysRevE.68.020901. [DOI] [PubMed] [Google Scholar]
- 24.Moreau L, Sontag E, Arcak M. Feedback tuning of bifurcations. Syst Control Lett. 2003;50:229–239. [Google Scholar]
- 25.Nadrowski B, Martin P, Jülicher F. Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity. Proc Natl Acad Sci USA. 2004;101:12195–12200. doi: 10.1073/pnas.0403020101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Balakrishnan J. Self-tuning to the Hopf bifurcation in fluctuating systems. J Phys A Math Gen. 2005;38:1627–1652. [Google Scholar]
- 27.Ó Maoiléidigh D, Jülicher F. The interplay between active hair bundle motility and electromotility in the cochlea. J Acoust Soc Am. 2010;128:1175–1190. doi: 10.1121/1.3463804. [DOI] [PubMed] [Google Scholar]
- 28.Blackwell DL, Lucas JW, Clarke TC. Summary health statistics for U.S. adults: National health interview survey, 2012. Vital Health Stat. 2014;10:1–161. [PubMed] [Google Scholar]
- 29.Daniel E. Noise and hearing loss: A review. J School Health. 2007;77:225–231. doi: 10.1111/j.1746-1561.2007.00197.x. [DOI] [PubMed] [Google Scholar]
- 30.Ó Maoiléidigh D, Nicola EM, Hudspeth AJ. The diverse effects of mechanical loading on active hair bundles. Proc Natl Acad Sci USA. 2012;109:1943–1948. doi: 10.1073/pnas.1120298109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Roongthumskul Y, Fredrickson-Hemsing L, Kao A, Bozovic D. Multiple-timescale dynamics underlying spontaneous oscillations of saccular hair bundles. Biophys J. 2011;101:603–610. doi: 10.1016/j.bpj.2011.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fettiplace R, Kim KX. The physiology of mechanoelectrical transduction channels in hearing. Physiol Rev. 2014;94:951–986. doi: 10.1152/physrev.00038.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Corns LF, Johnson SL, Kros CJ, Marcotti W. Calcium entry into stereocilia drives adaptation of the mechanoelectrical transducer current of mammalian cochlear hair cells. Proc Natl Acad Sci USA. 2014;111:14918–14923. doi: 10.1073/pnas.1409920111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hirono M, Denis CS, Richardson GP, Gillespie PG. Hair cells require phosphatidylinositol 4,5-bisphosphate for mechanical transduction and adaptation. Neuron. 2004;44:309–320. doi: 10.1016/j.neuron.2004.09.020. [DOI] [PubMed] [Google Scholar]
- 35.Lumpkin EA, Hudspeth AJ. Regulation of free Ca2+ concentration in hair-cell stereocilia. J Neurosci. 1998;18:6300–6318. doi: 10.1523/JNEUROSCI.18-16-06300.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ricci AJ, Wu YC, Fettiplace R. The endogenous calcium buffer and the time course of transducer adaptation in auditory hair cells. J Neurosci. 1998;18:8261–8277. doi: 10.1523/JNEUROSCI.18-20-08261.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yamoah EN, et al. Plasma membrane Ca2+-ATPase extrudes Ca2+ from hair cell stereocilia. J Neurosci. 1998;18:610–624. doi: 10.1523/JNEUROSCI.18-02-00610.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Howard J, Hudspeth AJ. Mechanical relaxation of the hair bundle mediates adaptation in mechanoelectrical transduction by the bullfrog’s saccular hair cell. Proc Natl Acad Sci USA. 1987;84:3064–3068. doi: 10.1073/pnas.84.9.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Vollrath MA, Eatock RA. Time course and extent of mechanotransducer adaptation in mouse utricular hair cells: Comparison with frog saccular hair cells. J Neurol. 2003;90:2676–2689. doi: 10.1152/jn.00893.2002. [DOI] [PubMed] [Google Scholar]
- 40.Pickles JO. An Introduction to the Physiology of Hearing. 4th Ed Emerald Group; Bingley, UK: 2012. [Google Scholar]
- 41.Goutman JD, Elgoyhen AB, Gómez-Casati ME. Cochlear hair cells: The sound-sensing machines. FEBS Lett. 2015;589:3345–3361. doi: 10.1016/j.febslet.2015.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Guinan JJ. Olivocochlear efferents: Anatomy, physiology, function, and the measurement of efferent effects in humans. Ear Hear. 2006;27:589–607. doi: 10.1097/01.aud.0000240507.83072.e7. [DOI] [PubMed] [Google Scholar]
- 43.Cooper NP, Guinan JJ. Medial olivocochlear efferent effects on basilar membrane responses to sound. In: Nuttall AR, T Ren T, Gillespie PG, Grosh K, de Boer E, editors. Auditory Mechanisms: Processes and Models. World Scientific; Singapore: 2006. pp. 86–92. [Google Scholar]
- 44.Brown MC, Nuttall AL. Efferent control of cochlear inner hair cell responses in the Guinea-pig. J Physiol. 1984;354:625–646. doi: 10.1113/jphysiol.1984.sp015396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ruggero MA, Rich NC, Recio A, Narayan SS, Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J Acoust Soc Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lindner B, Dierkes K, Jülicher F. Local exponents of nonlinear compression in periodically driven noisy oscillators. Phys Rev Lett. 2009;103:250601. doi: 10.1103/PhysRevLett.103.250601. [DOI] [PubMed] [Google Scholar]
- 47.Arnold L. Random Dynamical Systems. Springer; Berlin: 1998. [Google Scholar]
- 48.Kao A, Meenderink SW, Bozovic D. Mechanical overstimulation of hair bundles: Suppression and recovery of active motility. PLoS One. 2013;8:e58143. doi: 10.1371/journal.pone.0058143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shlomovitz R, et al. Low frequency entrainment of oscillatory bursts in hair cells. Biophys J. 2013;104:1661–1669. doi: 10.1016/j.bpj.2013.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.d’Eysmond T, De Simone A, Naef F. Analysis of precision in chemical oscillators: Implications for circadian clocks. Phys Biol. 2013;10:056005. doi: 10.1088/1478-3975/10/5/056005. [DOI] [PubMed] [Google Scholar]
- 51.Woller A, Gonze D, Erneux T. The Goodwin model revisited: Hopf bifurcation, limit-cycle, and periodic entrainment. Phys Biol. 2014;11:045002. doi: 10.1088/1478-3975/11/4/045002. [DOI] [PubMed] [Google Scholar]
- 52.Qu Z, et al. Early afterdepolarizations in cardiac myocytes: Beyond reduced repolarization reserve. Cardiovasc Res. 2013;99:6–15. doi: 10.1093/cvr/cvt104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sturis J, et al. Phase-locking regions in a forced model of slow insulin and glucose oscillations. Chaos. 1995;5:193–199. doi: 10.1063/1.166068. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.