Features of genomic organization in a nucleotide-resolution molecular model of the Escherichia coli chromosome

Abstract

We describe structural models of the Escherichia coli chromosome in which the positions of all 4.6 million nucleotides of each DNA strand are resolved. Models consistent with two basic chromosomal orientations, differing in their positioning of the origin of replication, have been constructed. In both types of model, the chromosome is partitioned into plectoneme-abundant and plectoneme-free regions, with plectoneme lengths and branching patterns matching experimental distributions, and with spatial distributions of highly-transcribed chromosomal regions matching recent experimental measurements of the distribution of RNA polymerases. Physical analysis of the models indicates that the effective persistence length of the DNA and relative contributions of twist and writhe to the chromosome's negative supercoiling are in good correspondence with experimental estimates. The models exhibit characteristics similar to those of ‘fractal globules,’ and even the most genomically-distant parts of the chromosome can be physically connected, through paths combining linear diffusion and inter-segmental transfer, by an average of only ∼10 000 bp. Finally, macrodomain structures and the spatial distributions of co-expressed genes are analyzed: the latter are shown to depend strongly on the overall orientation of the chromosome. We anticipate that the models will prove useful in exploring other static and dynamic features of the bacterial chromosome.

INTRODUCTION

Recent years have seen substantial improvements in the scale and resolution with which vital biological processes are modeled. Computational approaches centered on Monte Carlo simulation and other numerical methods (1–3) have allowed the description of the association, diffusion and reaction of limited sets of molecules on a cellular scale, and models of the bacterial cytoplasm have covered an expanding roster of cellular proteins (4–7). Continued progress toward a complete model of a bacterial cell, however, will require the inclusion of an element cytoplasmic simulations have not yet been able to accommodate: an accurate structural model of the chromosome. The challenge that modeling the chromosome represents is substantial: the Escherichia coli chromosome, for example, includes over 4.6 million base pairs (Mb) of DNA, with a contour length of 1.6 mm compressed into a cell <3 μm in length in a predictable orientation (8,9). It has long been appreciated, moreover, that DNA in the bacterial cell is not in a relaxed state, but is instead supercoiled due to a combination of topoisomerase activity (10) and protein binding (11,12). Because the conformation of the chromosome and the processes in which it acts as a template both depend on supercoiling, high-resolution modeling of its structure is ultimately likely to be essential.

Several prior studies have described models of the bacterial chromosome in conditions of cell-like confinement, either at full genomic length and low resolution, or at subgenomic length and higher resolution. Models developed according to the former strategy typically include—or seek to reproduce—experimental data on bacterial chromosomes at the cellular scale. For Caulobacter crescentus (13), and very recently for Mycoplasma pneumoniae (14), for example, chromosomal contact data have been incorporated into model chromosomes as restraining potentials acting between interacting loci; for C. crescentus, these same data have also been used to test the degree to which boundaries between interaction domains depend on intervening regions of high transcriptional activity (15,16). For E. coli, full-length, coarse-grained (CG) representations of the chromosome have been used to explore the effects of: macrodomain (MD) condensation (17), the linear organization of chromosomal loops (18) and the specific positioning of DNA loci (19), on the chromosome's global arrangement. These latter models have represented the chromosome as an unbranched, annular structure, but studies representing it instead as a hyper-branched chain—which may more closely resemble the chromosome in vivo—have also been used to assess the contribution of configurational entropy to ribosome-nucleoid segregation (20,21).

Several other large-scale models have sought to capture the observed behavior of the bacterial chromosome more phenomenologically, using a deliberately generic polymer physics framework to describe, for example, chromosomal conformations as a function of the density of bridging interactions (22,23), or the tendency of replicated rings to separate under confinement (24), without making strict reference to the genomes of actual organisms. Although these more generic models do not attempt to explicitly include supercoiling or to map polymer beads to genomic coordinates, they underline a fundamental challenge in designing models that can be integrated into whole-cell simulations: success in reproducing cellular-level effects generally comes at the price of limited structural resolution, with single ‘beads’ in the models typically representing ∼1000–10 000 basepairs (bp), which in turn precludes detailed modeling of plectonemic supercoils or protein binding.

In comparison, the higher level of structural resolution available to subgenomic models, which typically feature polymers of up to ∼40 000 bp modeled by beads representing 7–30 bp, offers two significant advantages. First, higher resolution allows the effects of protein–DNA interactions to be modeled in a much more natural way: while it is possible to mimic protein-mediated bridging interactions by applying restraining potentials between selected pairs of DNA beads (see above; (22,23)), in higher-resolution models the bridging proteins can instead be modeled explicitly using additional beads (25,26). Second, more detailed subgenomic models significantly facilitate the modeling of DNA supercoiling and its effects on chromosomal compaction. Recent studies along these lines have explored: the role of supercoiling in defining chromosomal shape in crowded conditions (27), the role of supercoiling in encouraging enhancer–promoter interactions (28), the effects of extreme local supercoiling densities created in the vicinity of active RNA polymerases (RNAPs) (29) and the scaling of interlocus distances in supercoiled DNA under cell-like confinement (30). Such subgenomic models allow important new insights to be gained, therefore, but they are typically not designed to simultaneously incorporate cellular-scale experimental data from a range of different sources.

In an attempt to bridge the gap between the lower-resolution genomic models and the higher-resolution subgenomic models described above, we report here structural models of entire E. coli chromosomes at resolutions of one nucleotide per bead (1 NTB) confined within the experimentally-determined volume of the nucleoid. Importantly, the models attempt to combine fidelity to a wide range of available experimental data, with a resolution sufficient for exploration of local physical properties. At a macroscopic level, the models resolve the chromosome into the topologically distinct ∼10 kb domains described for E. coli (31), and into the higher-order ∼100–200 kb interaction domains suggested by studies of chromosomal contacts in C. crescentus (15,32). Additionally, by exploiting both ChIP–chip data (33) and single-molecule fluorescence data (34), they correctly reproduce the drastically different spatial distributions of transcribing RNAP molecules and bulk DNA within the nucleoid of E. coli. At a more microscopic level, the models reproduce the experimental distributions of plectoneme lengths and branching patterns (35), the persistence length of DNA (36) and they provide geometrically realistic distributions of major and minor groove widths. Finally, at a topological level, the models produce a realistic partitioning between twist and writhe (35) while giving an overall supercoil density that lies in the middle of the wide range of values reported for the E. coli chromosome (37–39). In what follows we outline the principles guiding the development of the models, characterize their physical properties and macroscopic features and discuss the role that such high-resolution models of the bacterial chromosome can play in studies aimed at more fully understanding the inner workings of the cell.

MATERIALS AND METHODS

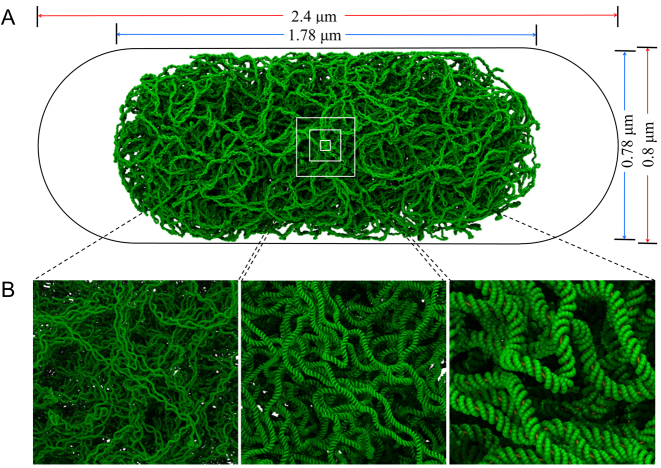
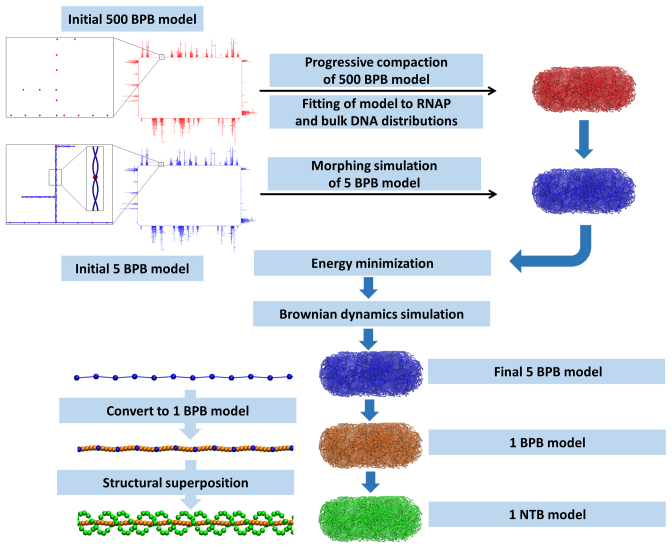
An example chromosome structure is shown at increasing levels of magnification in Figure 1A and B; the complete set of structures that we have generated appears in Supplementary Figures S1 and 2. Each structure represents a single E. coli chromosome, modeled under conditions appropriate to slow growth and generated using multi-scale simulation techniques with CG models operating at several different levels of resolution (Figure 2). The protocol used to generate the structures, and the rationale behind their design, are described fully in the Supplementary Data. Here we describe their construction in outline.

Figure 1.

Structural model of the Escherichia coli chromosome. (A) A model of the 4.6 Mb E. coli chromosome at 1-nt resolution (green) pictured within a volume corresponding to the cell (black outline). Dimensions appearing above and at right are those of the nucleoid (blue) and the cell containing it (red). (B) Images of the chromosome at increasing magnification. In the left panel, individual plectonemes appear; in the right panel, distinct major and minor grooves are visible.

Figure 2.

A schematic of the protocol used to build models of the chromosome. A 500 base-pair-per-bead (BPB) structure is progressively compacted into the nucleoid volume, defining a path for higher resolution structures to follow. Initial 500 BPB (red) and 5 BPB (blue) ‘blueprint’ structures appear at upper left; the insets for the 5 BPB structure show supercoiled duplexes in part of a single plectoneme. Full details of the process are given in Supplementary Data.

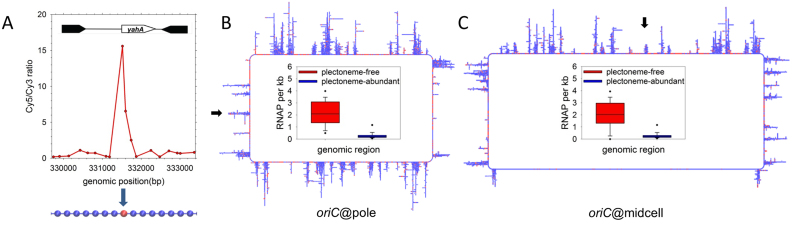
Following arguments advanced by the Laub group (15), Higgins group (40) and Jin group (41) we have taken a ‘transcription-centric’ approach, in which the structure of the chromosome is assumed to be defined to a substantial degree by its transcriptional profile. In particular, inspired by the ‘bottlebrush’ model proposed by the Laub group for C. crescentus (15), we partition the chromosome into a series of negatively supercoiled, plectoneme-abundant regions (PARs), interspersed by shorter plectoneme-free regions (PFRs), with the latter assumed to correspond to regions of high transcriptional activity. We assign regions of DNA to PARs or PFRs based on ChIP–chip data for RNAP reported for E. coli in slow-growth conditions (33) (Figure 3A–C) and for which we can justifiably construct models consisting of single, unreplicated chromosomes (42). Reflecting their likely physiological significance, we have constructed two distinct sets of models of the chromosome that can be distinguished by their positioning of the origin of replication, oriC: from here on, these are termed the oriC@pole (Figure 3B) and oriC@midcell (Figure 3C) models. The experimental evidence suggesting that both of these global arrangements may be important in slowly-growing cells appears in Supplementary Data.

Figure 3.

Design of initial ‘blueprint’ models. (A) Incorporation of ChIP data defining RNAP binding sites (data obtained and figure adapted from (33)). ChIP-determined binding peaks were used to assign identities to beads in the 500 BPB model (lower portion of panel): RNAP beads (beads whose sequence includes a RNAP binding site) appear in red; bulk DNA beads are blue. (B) A representative 500 BPB oriC@pole ‘blueprint’ structure. Regions of active transcription, as indicated by ChIP data, are plectoneme-free regions (PFRs), while the balance of the genome is plectonemic (PARs). oriC is located at the pole of the cell (black arrow on left side of the ‘blueprint’); the inset describes the difference in RNAP density between PFRs and PARs. (C) A representative 500 BPB oriC@midcell ‘blueprint’ structure. The origin is located in the center of the upper arm of the chromosome (black arrow above the ‘blueprint’); the bottom ‘crossing’ region (71) is modeled as plectoneme-free.

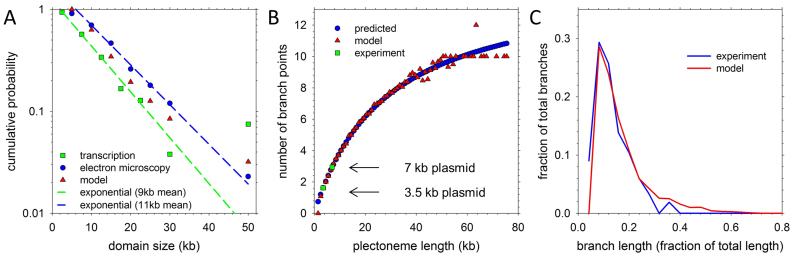
For both the oriC@pole and oriC@midcell models, we have built 20 structures that each use the same defined locations of PARs and PFRs but that each differ in their plectoneme lengths, branches and positions: to model plectonemes as realistically as possible, we assigned their lengths so as to reproduce the exponential distribution determined experimentally for E. coli (31) and incorporated branches in a way that explicitly matches the frequencies and lengths observed in supercoiled plasmids (35) (Figure 4A–C). For each of the 20 chromosome structures that was built for the oriC@pole and oriC@midcell models, an initial, idealized atomic structure was first constructed, 1 bp at a time, with the twist angles at basepair steps in the PARs reduced slightly from their standard B-DNA values of 34.3° in order to produce an overall supercoiling density, σ, of −0.05. These idealized structures serve as ‘blueprints’ that are intended only to define the overall topology and connectivity of the chromosome models and to provide initial coordinates for a subsequent series of simulations that seek to compress the chromosome within the confines of the nucleoid region of the cell. Within each idealized structure, all PFRs are represented by linear B-DNA, all plectoneme stems and branches within PARs are uniformly twisted with a super-helical pitch roughly matching theoretical predictions made by Marko and Siggia (43), and all transitions between PFRs and PARs consist of smoothly bent B-DNA (Figures 2; 3B and C).

Figure 4.

Distribution of plectoneme and branch lengths. (A) Distribution of plectoneme lengths. Model plectoneme lengths (red triangles) fall between experimental fits to exponential distributions with mean lengths of 9 kb (based on transcriptional activity of supercoiling-sensitive genes; in green) and 11 kb (based on analysis of EM images; in blue) (figure adapted from (31)). (B) Branch count (red) as a function of plectoneme length compared to predictions based on plasmid branching (blue). Mean experimental branch counts for plasmids of lengths 3.5 and 7 kb (35) are in green. (C) Distribution of fractional branch lengths of simulated 7 kb plectonemes (red) compared with experimental lengths in a negatively-supercoiled 7 kb plasmid ((35); in blue). Further discussion of the alternative global orientations and details of the derivation of branching patterns from experiment appear in Supplementary Data.

Each idealized chromosome structure was used to generate three independent CG models, ranging from a 1 NTB model at the finest level of detail, through an intermediate 5 bead-per-basepair (BPB) model, to a 500 BPB model at the coarsest level of detail. All three of these models were used to generate the final chromosome structures reported here. First, each 500 BPB structure was subjected to a series of Brownian dynamics (BD) simulations that sought to compress the chromosome within the nucleoid, which we modeled here as a cylinder of length 1.0 μm and radius of 0.4 μm, capped at either end by hemispheres of the same radius (see Supplementary Data). To retain accuracy in the representation of the physical properties of the DNA polymer during these simulations, the energy model used in the simulations was first parameterized to reproduce the persistence length of double-stranded B-DNA (Supplementary Figure S3A). Once successfully positioned, the population of twenty 500 BPB structures was simultaneously subjected to a second round of simulations in which biasing potentials were added to drive the positions of the beads so as to match the different spatial distributions of DNA and transcribing RNAP molecules recently observed in E. coli by the Kapanidis group (34). By matching these data, therefore, the final structures we report should account implicitly for the combined effects of macromolecular crowding (44) and nucleoid-associated proteins (NAPs; (45)) even though they do not, at this stage, explicitly include NAPs. Notably, while closely aligned with the experimental data in aggregate (Figure 5A and B), the 20 structures built for each type of model display substantial variations (Supplementary Figure S4).

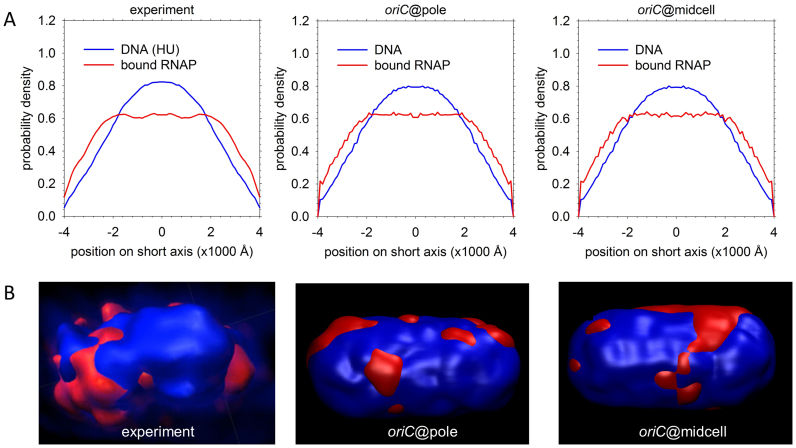
Figure 5.

Reproduction of experimental DNA and RNAP density data. (A) Short-axis distributions of bound RNAP (red) and DNA (indicated by nonspecific HU binding; blue). The left panel shows experimental data for cells grown in minimal medium (34), while the two right panels depict population averages of these distributions for the sets of oriC@pole and oriC@midcell structures. (B) Left: experimental 3D surface rendering of a nucleoid from a cell grown in minimal medium, with DNA (indicated by HU binding) in blue and bound RNAP in red (figure reproduced from (34)). Panels on the right are surface renderings of two representative 500 BPB structures in which bulk DNA is blue and RNAP-bound DNA is red. [Reproduced in part from Stracy,M., Lesterlin,C., de Leon,F.G., Uphoff,S., Zawadzki,P. and Kapanidis,A.N. (2015) Live-cell superresolution microscopy reveals the organization of RNA polymerase in the bacterial nucleoid. Proc. Natl. Acad. Sci. U.S.A., 112, E4390–E4399.].

Next, the trajectories followed by the 500 BPB structures during the above simulations were used as guides in a series of ‘morphing’ simulations that were applied to each of the 5 BPB structures. Each stage of morphing consisted of an energy minimization of an elastic network model (46) that included: (i) harmonic restraints between each 5 BPB bead and the nearest 500 BPB bead, and (ii) harmonic restraints between all pairs of 5 BPB beads that were initially separated by <100 Å. The former set of restraints acts to encourage the 5 BPB structure to follow closely the trajectory originally traced by the 500 BPB structure; the latter set of restraints acts to encourage the 5 BPB structure to preserve its plectonemic framework during the morphing process. Once morphing was completed, the elastic network restraints were removed, a more sophisticated energy model (incorporating steric and electrostatic interactions) was introduced, and additional energy-minimizations and BD simulations were performed to regularize each of the 5 BPB structures. Again, the energy model during these latter simulations was first parameterized to reproduce the persistence length of B-DNA (Supplementary Figure S3B and C).

Finally, each 5 BPB chromosome structure was converted into a structure with 1 NTB resolution using a series of structural superpositions combining information from the finalized 5 BPB structure and the initial 1 NTB structure. First, four intermediate beads were added between each pair of connected beads in the 5 BPB structure and then energy-minimized, thereby defining a double-helical axis for all 4.6 million basepairs. Next, DNA fragments extracted from the initial 1 NTB structure were progressively superposed onto the double-helical axis so as to build a final 1 NTB structure one basepair at a time. The resulting 1 NTB structure was then subjected to a short final energy minimization in case any steric clashes or structural discontinuities arose during the superposition process.

Full details of the above procedure, and full descriptions of all methods used to analyze the resulting structures, are provided in the Supplementary Data. The final chromosome structures are available from the authors upon request.

RESULTS AND DISCUSSION

Physical properties of the high-resolution models

The macro- and mesoscopic features that have been explicitly ‘built in’ to the chromosome models are described above and in detail in the Supplementary Data. To verify that the final structures are reasonable at a microscopic level, however, we have analyzed a variety of their structural properties. For both the oriC@pole and oriC@midcell models, the distributions of the major and minor groove widths sampled over the entire chromosome match well with estimates from nuclear magnetic resonance and atomistic simulations of DNA oligonucleotides (47) (Supplementary Figure S5A and B). The distributions of local DNA bend angles, on the other hand, are very similar to those predicted by a worm-like chain (WLC) model (48) with best-fit persistence lengths of 495 and 496 Å for the oriC@pole and oriC@midcell models, respectively (Supplementary Figure S5C and D); these are in excellent agreement with the experimental estimate of 500 Å for B-DNA at physiological ionic strength (36). Finally, the mean-squared end-to-end distances of the DNA in the PFR regions of the structures yield average persistence lengths of 522 and 569 Å for the oriC@pole and oriC@midcell models, respectively, again in good agreement with experiment in vitro for B-DNA. While we obtain much shorter values when we measure the apparent persistence length of the entire chromosomal DNA (see below), each of these results indicates that the nucleotide-resolution structures obtained after compaction into the nucleoid region of the cell are free of significant conformational strain.

The high resolution of the 1 NTB structures allows supercoiling to be analyzed naturally, with the only difficulty arising from the expense of the calculations. Methods have been reported recently by the Tobias group (49) and Noy group (50) that allow each of the three key supercoiling parameters (Linking Number (Lk), Twist (Tw) and Writhe (Wr) (51)) to be accurately computed from atomic structures of DNAs. Using versions of these codes that have been tested on plasmids (Supplementary Table S1), and parallelized in-house, we have computed Tw and Wr for all 40 complete chromosome structures and have checked the accuracy of the resulting values by performing the more expensive calculation of Lk on a single chromosome structure and using Lk = Wr + Tw. The calculated values of Tw and Wr for all structures are listed in Supplementary Tables S2 and 3 for the oriC@pole and oriC@midcell models, respectively. The mean supercoil density, σ, is −0.049 ± 0.0004 for both types of model, which is near the middle of the wide range of values reported for the E. coli chromosome (37–39). Finally, the mean relative contributions of Tw and Wr to this negative supercoiling are found to be in the ratios 35:65 and 39:61 for the oriC@pole and oriC@midcell models, respectively. These values agree quite well with the 28:72 ratio deduced by Boles et al. from analysis of electron micrographs of supercoiled 7 kb plasmids (35), and with the results of atomistic simulations on plasmids indicating that, while the Tw:Wr partition is ∼50:50 for DNA minicircles (<350 bp) (50), in longer plasmids the partition becomes closer to ∼33:67 (52,53).

Void distributions

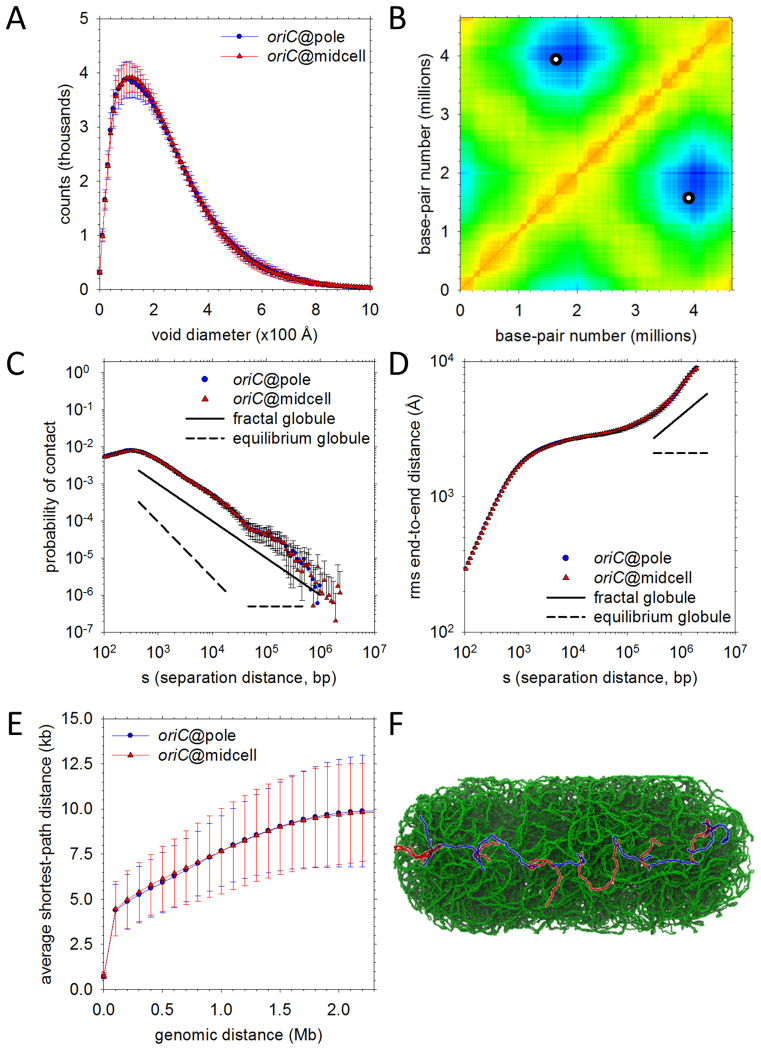
One important question that the structures can be used to answer directly is the extent to which compaction of the chromosome into the nucleoid region leaves interior space open to large macromolecular complexes such as ribosomes. Figure 6A shows the distribution of void diameters accessible within the interior of the nucleoid, averaged over the 20 structures for both the oriC@pole (blue) and oriC@midcell (red) models. With both types of model, broad distributions are obtained, with mode void diameters of ∼150 Å but with substantial populations of much larger void diameters (as high as ∼800 Å). This suggests, consistent with the results of recent single-molecule imaging studies of ribosomal subunits in E. coli (54), that, at least as far as excluded-volume effects (only) are concerned, some regions of the nucleoid interior are likely to be accessible even to large macromolecular complexes.

Figure 6.

Physical properties of the final high-resolution models. (A) Distributions of void sizes in the oriC@pole (blue) and oriC@midcell (red) models. (B) A contact map (‘heat map’) for the oriC@pole model set. Mean distances between chromosomal loci binned into 10 kb blocks are plotted; the color in each x-y (locus–locus) bin reflects the distance between those loci on a scale ranging from red (distance = 0) to blue (distance = maximum measured distance). Points on the map that would denote contacts between oriC and a genomically-opposite locus within ter appear as two (equivalent) white circles. (C) Probability of contact as a function of genomic separation. Plots for oriC@pole (blue) and oriC@midcell (red) models are compared to ideal plots representing fractal globule (solid line) and equilibrium globule (dashed line) scaling behavior. Probability of contact in the ideal fractal globule scales as s⁻¹ over a substantial range of separations, while the equilibrium globule probability initially scales as s^−3/2 before assuming a constant value at longer separations. (D) Same as (C), but comparing root-mean-square end-to-end distances. The idealized scaling exponents represented are s^1/3 (fractal globule) and s⁰ (equilibrium globule). (E) Shortest paths between genomic loci. Mean shortest paths as a function of genomic separation are plotted for oriC@pole (blue) and oriC@midcell (red) models. Path lengths are determined by solving for the shortest path comprising only 1D diffusion along DNA and intersegmental jumps between regions in close physical contact (see Supplementary Data for details). (F) Example of the shortest path between loci at opposite nucleoid poles. An intersegmental jump between different plectonemic regions is represented as a color change from blue to red or red to blue along the path.

The broad range of void sizes reflects the non-uniform distribution of DNA density in the structures. Histograms of the DNA density sampled in cubes of side-length 50 Å show a peak at ∼140 mg/ml for both the oriC@pole (blue) and oriC@midcell (red) models (Supplementary Figure S6A). The highest densities found correspond to ∼300 mg/ml (Supplementary Figure S6B), which, while high, are still well below the ∼500 mg/ml concentration found in viral capsids (55); visual examination of one such high density region shows that it corresponds to a nexus of closely-spaced plectonemes (Supplementary Figure S6C). Sampling the DNA density at a coarser level of resolution (1000 Å) provides views of the chromosome that can be compared with those available from high-resolution microscopy (Supplementary Figure S6D); the resulting density maps are at least superficially similar to experimental 3D images suggesting a ‘helix-like’ distribution of DNA density (56).

Inter-locus distance distributions

A consistent characteristic of the chromosomal structures is the close approach that can occur between loci that are genomically very distant. Figure 6B shows a ‘heat map’ of the average distances between 10 kb segments of the chromosome in the oriC@pole model. Close contacts, which are indicated by red-yellow regions on the maps, occur primarily along the diagonal, in blocks that correspond to the PARs (similar to what has been reported previously for C. crescentus by the Laub group (15)), but they also occur along the anti-diagonal, where they correspond to pairs of loci that are at similar positions along the chromosome's ‘arms.’ The furthest distances (blue regions) occur, as expected given the nature of the oriC@pole model, between the oriC and ter regions of the chromosome since these are positioned at opposite ends of the nucleoid (see circles on Figure 6B). Qualitatively similar results are obtained for the oriC@midcell model (Supplementary Figure S7) but the details differ owing to the very different global orientation of the chromosome.

The chromosomal models have features similar to those of a fractal globule

In eukaryotic cells, studies have suggested that the DNA polymer may assume characteristics of a ‘fractal globule’ (57,58); CG simulations of a reduced Caulobacter chromosome model suggest that such a state may also be relevant to prokaryotic cells (30). The fractal globule is a long-lived, non-equilibrium state of hierarchically-organized ‘crumples’: the formation of crumples in an initially-linear polymer generates a second, thicker ‘chain,’ which in turn is subject to crumpling, producing yet another chain in an iterative folding process that culminates in the formation of a self-similar spherical globule (59). In its idealized form, the fractal globule is devoid of knots, while the so-called ‘equilibrium globule’ (a uniform-density state that results from continued diffusive slithering of a polymer over a long timescale) is highly entangled (58,60). Although the extreme complexity of our structures prevents us from being certain of the extent to which they contain knots (see Supplementary Data), it remains of interest to ask whether they exhibit other properties similar to those of a fractal globule. To this end, we analyzed the scaling of contact probabilities and root-mean-square distances between loci as a function of their genomic separation, s, since both properties exhibit characteristic scaling behaviors in the fractal globule model.

With regard to contact probabilities, the packaging of the vast majority of the chromosome into plectonemes complicates interpretation at very short genomic separations, but beyond 1 kb we find that the contact probabilities scale robustly as s⁻¹ for separations up to 2 Mb. This is entirely consistent with the behavior expected of a fractal globule (Figure 6C). Strikingly, this scaling is also in good agreement with the results of in vivo gene regulation experiments using the LacI repressor, for which a plot of the effective molar concentration of interacting sites versus genomic separation fits to a power law with an exponent of −1.15 (61). While not explicitly identified as such in ref. 61, therefore, the behavior seen in the gene regulation experiments appears to be consistent with a fractal organization of the E. coli chromosome. With regard to the scaling of the root-mean-squared end-to-end distances, the result is somewhat more ambiguous since it only shows the s^−1/3 scaling expected of a fractal globule (58) at genomic separations >100 kb (Figure 6D); interestingly, similar behavior has been reported for eukaryotic chromosomes (62). Importantly, neither the contact probabilities nor the end-to-end distances fit well to expectations based on the alternative model of an ‘equilibrium globule’ (Figure 6C and D).

Before moving on, we note that, in addition to offering information about the global state of the chromosome, contact probabilities can also be used to provide an estimate of the apparent persistence length of chromosomal DNA that is well suited to comparison with gene regulation experiments. In particular, if the DNA is modeled as a WLC, the probability that a segment will assume a given end-to-end distance (in this case, <100 Å) becomes an analytical function of its contour and persistence lengths (see Supplementary Data; (63)). Performing such an analysis over the entire chromosome—i.e. including both plectonemic and non-plectonemic regions—we find apparent persistence lengths ranging from 86 to 149 Å for loci separated by 246 to 530 bp, with the apparent persistence lengths declining as genomic separation increases in accord with the s⁻¹ scaling described above. These values can be compared with apparent persistence lengths that quantify DNA looping in gene regulation experiments using, for example, the approach described by the Stewart group (64). For E. coli, persistence length estimates derived from gene regulation experiments range from ∼70 Å for operators separated by short (∼100 bp) distances (65,66), to ∼230 Å for sites separated by up to 10 kb (61). We note that the much lower apparent persistence length obtained when calculated over the entire chromosome relative to that reported above for PFRs (∼500 Å) reflects the packaging of the vast majority of the chromosomal DNA into branched plectonemes in which the DNA frequently doubles back on itself. Consistent with both experiments (67) and simulations (28), the probability of contact between interacting sites increases dramatically when plectonemes are formed due to supercoiling.

Shortest-path analysis for genomically distant loci

In all of the structures, it is notable that individual plectonemes can form very close contacts (<50 Å between the double-helical axes) with multiple plectoneme partners. Supplementary Figure S8 shows that the mean number of plectonemes in contact with any particular plectoneme increases monotonically with the latter's length, with the longest plectonemes (∼40 kb in length) contacting, on average, ∼40 different plectonemes. One intriguing possibility raised by this high frequency of inter-plectonemic contacts is that DNA-binding proteins might be able to efficiently scan the chromosome by continually transferring from one plectoneme to another, perhaps using the ‘monkey-bar’ mechanism of inter-segmental transfer proposed by the Levy group (68).

To explore this idea further, we have used 2D maps of the DNA–DNA contacts <50 Å to determine the set of shortest paths that connect all possible pairs of chromosomal locations, assuming that each path consists only of linear (1D) diffusion along the DNA, coupled with inter-segmental jumps between genomically distant locations at points of close physical contact. Figure 6E shows how the average shortest path-length between loci depends on the genomic distance between them. The slope of the curve is extraordinarily shallow: for loci that are separated by as much as 2 Mb, for example, the shortest path-length averages only ∼10 kb, which implies a 200-fold decrease in the length of the DNA that, in principle, would need to be searched if linear diffusion along the DNA was the only mechanism allowed. An example of one such path is provided in Figure 6F, which shows that two loci at opposite ends of the cell can be connected physically by a path that involves inter-segmental jumps between 15 different plectonemic regions. While DNA-binding proteins are thought to use a combination of mechanisms to efficiently search for chromosomal locations (69)—including, of course, 3D diffusion, which is not considered in the above analysis—the present high-resolution models of the bacterial chromosome suggest that inter-segmental jumps may warrant further attention.

Spatial distributions of genes and operons

Since the locations of all 4.6 million basepairs are known explicitly in the chromosome structures, it is possible to directly visualize the 3D distribution of any genomic locus of interest; Figure 7, for example, illustrates how operons (70) are spatially distributed in the most representative oriC@pole and oriC@midcell structures. In order to compare more closely with experimental data, however, it is typically necessary to re-express these 3D distributions as 2D projections along the long-axis or short-axis of the cell. The long-axis distributions of uniformly sampled genomic loci, for example, can be compared with the corresponding experimental distributions reported by the Wiggins and Kondev groups (71). For the oriC@midcell model, which is architecturally the most consistent with their fluorescence data, we find rather good agreement for all but the most pole-proximal loci (Supplementary Figure S9A). We can also examine the spatial locations of the extended protein occupancy domains (EPODs) identified by the Tavazoie group (72), in this case, focusing on their radial distributions. Encouragingly, we find that those EPODs associated with the highest RNA expression levels are noticeably shifted outward in both oriC@pole and oriC@midcell models (Supplementary Figure S9B); this is entirely in accord with the outward shift in the radial distribution of RNAP observed experimentally (34). Since the EPOD data were not used in the construction of the chromosome models, this demonstrates a substantial degree of self-consistency between the RNAP ChIP-chip data (33), the RNAP single-molecule fluorescence data (34), the EPOD data (72) and the structural models presented here. In passing, we note that we also analyzed the radial distributions of genes grouped according to the subcellular locations of their protein products, but found no significant differences between any of the four groups analyzed (Supplementary Figure S9C).

Figure 7.

Distribution of operons in the chromosome models. (A) The positions in the most representative oriC@pole structure of all operons listed in RegulonDB (70) that contain at least two genes are depicted: each such operon is represented as a single color assigned by cycling through a 7-element spectrum over the list of 851 operons. Regions not covered by multigene operons are represented in white. (B) Same as (A), but for the most representative oriC@midcell structure.

Macrodomain organization

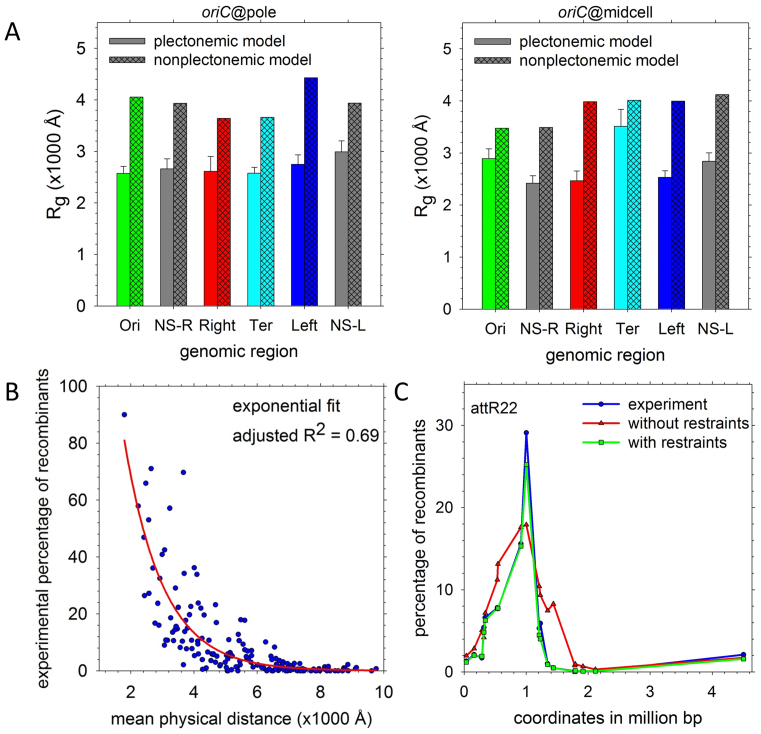
At a macroscopic level, the E. coli chromosome is thought to be organized into higher-order structures comprising hundreds of thousands of basepairs: in particular, a number of studies (17,73–75) suggest that the chromosome can be resolved into four insulated MDs—Ori, Ter, Left and Right—and two more-loosely-structured regions—NS-L and NS-R—flanking oriC. Since we did not initially seek to explicitly build MDs into our chromosome structures (see below), it is interesting to note that features consistent with them arise naturally during construction of the models. Specifically, the four chromosomal regions corresponding to the MDs automatically segregate from each other (Supplementary Figures S1 and 2), and occupy well-defined positions within the nucleoid (Supplementary Figure S10; (74)). In addition, in comparison with a reference, non-plectonemic chromosome structure that was also matched to the experimentally derived radial distribution of DNA density (see Supplementary Data), the MD regions in the oriC@pole and oriC@midcell models assume significantly more compact conformations (Figure 8A). But since similar effects are also obtained with the NS regions (Figure 8A)—which studies suggest should be much more loosely structured (75)—much of the observed behavior appears to reflect a generic feature of the models, namely their heavy emphasis on packaging of the DNA into plectonemes.

Figure 8.

Macrodomain organization in the chromosome models. (A) Radii of gyration of each of the regions defined by Valens et al. (75) in the ‘true,’ plectonemic model sets (solid bars) compared with those of a non-plectonemic model with equivalent positioning of oriC (hashed bars). (B) Recombination frequencies from Valens et al. (75) plotted versus the mean physical distances between the recombining loci in the 40 chromosome structures (blue); the red line indicates a single-exponential fit to the data. (C) A representative plot of recombination frequencies predicted by mean physical distance in the structures before (red) and after (green) imposition of distance restraints compared with the experimentally-determined frequencies (blue). Experimental data are from (75); analogous plots for other recombining loci appear in Supplementary Figure S11.

One way in which a more pronounced difference between the MDs and NS regions might, in principle, be generated is through the incorporation of distance restraints intended to match experimental data. An experimental finding central to the development of the MD concept was the occasionally-anomalous dependence of recombination frequencies on the genomic distance separating the recombining loci (75). Importantly, the structures generated here allow the experimental recombination frequencies to be expressed instead in terms of the physical distances between the loci. The data can be fit to an exponential decay function with a decay constant of 1221 bp^–1 (Figure 8B), and the resulting recombination frequencies predicted directly from the chromosome structures (red symbols in Figure 8C) are generally in rather good agreement with the experimental values (blue symbols) (see Supplementary Figure S11 for all comparisons). Closer agreement can, however, be achieved: the quantitative relationship established in Figure 8B allows the experimental recombination frequencies to be converted into target separation distances for each locus-pair, which can then be implemented as restraints in additional simulation stages. Using this approach (see Supplementary Data), we have produced a second set of structures that successfully reproduces the target distances (see green symbols in Figure 8C and Supplementary Figure S11). Despite now satisfying all of the available experimental data, however, the overall level of structuring of the MD and NS regions remains essentially unchanged (Supplementary Figure S12). More accurate modeling of MD organization in future iterations of the chromosome models, then, may require knowledge of the relative plectoneme density in MD and NS regions, chromosomal contact data (32) and/or additional information about the location of potentially domain-defining proteins.

Relative gene positioning

The circular nature of the bacterial chromosome means that sophisticated analysis of the relative positions of genes in E. coli is possible even in the absence of in vivo localization data (76–78). While recent studies have begun to incorporate chromosomal contact data as well (79), the structures reported here provide an opportunity to extend this work by enabling the direct translation of genomic distances into measurable physical distances.

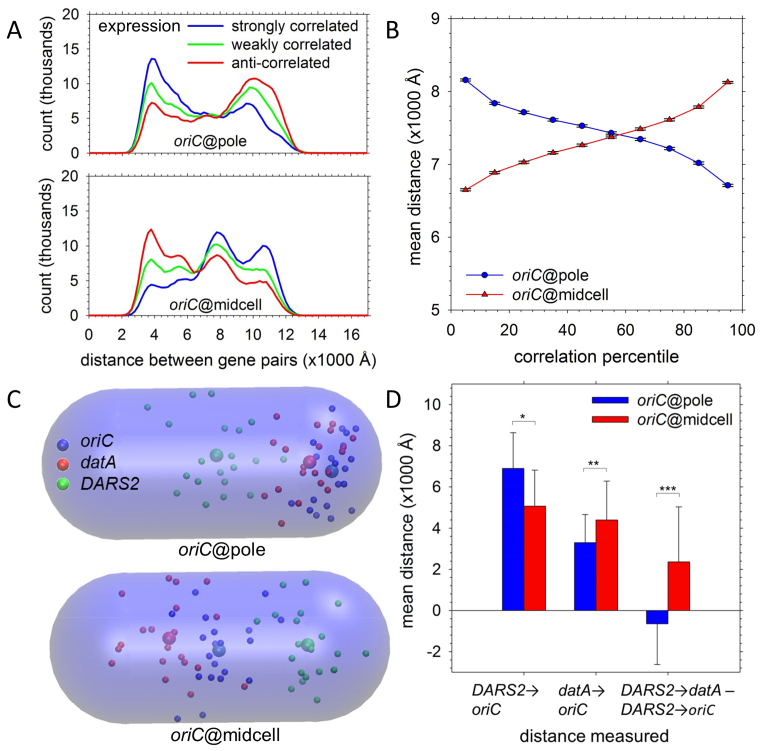
We consider first the relative physical distances between biologically linked gene pairs in the oriC@pole and oriC@midcell models. Using data from the M3D database (80), we find that for gene pairs separated by at least 1.5 Mb, surprising differences emerge depending on the genes’ RNA expression profiles. In the oriC@pole model (Figure 9A, upper panel), gene pairs with strongly correlated expression profiles (blue) tend to be positioned relatively closely, while gene pairs with strongly anti-correlated expression profiles (red) tend to be separated by much greater distances; gene pairs with very weakly correlated expression profiles (green), on the other hand, show intermediate behavior. Given the known tendency for linked genes to interact in trans across replichores (78), the close physical proximity of highly-coexpressed genes in the oriC@pole model is perhaps unsurprising. More striking is the evident separation of these genes in the oriC@midcell conformation (Figure 9A, lower panel), while genes whose expression levels are anti-correlated tend to be closer. These opposing trends contribute to stark differences between the models: as shown in Figure 9B, the mean separations of gene pairs in the two types of model differ substantially across the entire range of coexpression levels. Interestingly, gene pairs whose separation depends most strongly on the chromosomal orientation are those at the extremes of the correlation range (Supplementary Figure S13). We also find that the differences apparent in Figure 9A are sharply reduced when reference, non-plectonemic structures are analyzed instead (Supplementary Figure S14), suggesting that the proposed ‘bottlebrush’ arrangement of the chromosome (15), with the constituent plectoneme lengths following a defined distribution (31), may play a role in dictating the precise positioning of co-regulated genes.

Figure 9.

Gene and regulatory element positioning. (A) Distribution of the mean distances between gene pairs separated by 1.5 Mb whose coexpression was ranked in the top 10% (blue), middle 10% (green) and bottom 10% (red) of all gene pairs by Pearson correlation coefficients. Upper panel shows results for the set of 20 oriC@pole structures; lower panel shows results for the set of 20 oriC@midcell structures. (B) Mean distances for 10 deciles of coexpression profiles are plotted for oriC@pole (blue) and oriC@midcell (red). Gene pairs were grouped into deciles by the Pearson correlation coefficient of their expression profiles; as plotted, the correlation coefficient (strength of co-expression) rises from left to right. Error bars indicate the 99.9% confidence interval for each mean. (C) Spatial positions of oriC (blue), datA (red) and DARS2 (green) in the 20 individual structures are plotted as small spheres; larger spheres represent the mean position of each locus in the indicated global model type. The transparent capsule corresponds to the nucleoid volume. (D) At left, mean distances to oriC are plotted for DARS2 and datA in oriC@pole (blue) and oriC@midcell models (red). At right, mean differences between the DARS2-to-datA distance and DARS2-to-oriC distance are plotted for oriC@pole (blue) and oriC@midcell (red). P-values were calculated with Welch two-sample t-tests (*P < 0.05; **P < 0.005; ***P < 0.0005).

The differences between models depicted in Figure 9A are consistent with the possibility of a genome-wide restructuring of relative gene-positioning occurring as the cell moves from the oriC@pole to the oriC@midcell conformation in preparation for replication (42). Interestingly, this possibility is reinforced by changes that we observe in the disposition of regulatory elements known to be crucial to the initiation of replication. A key step in initiation is the assembly at the origin, oriC, of multiple copies of the DnaA protein in its adenosine triphosphate (ATP)-bound state (DnaA^ATP) (81). Two non-coding sites on the chromosome act to regulate the availability of DnaA^ATP: these are datA, which promotes DnaA^ATP hydrolysis and thereby acts to prevent repeated or premature initiation events (82), and DARS2, which promotes regeneration of the ATP-bound state and thereby tilts the balance in favor of initiation (83). Bioinformatics analyses indicate that, relative to oriC, the genomic positions of both datA and DARS2 are strongly conserved among E. coli strains (84,85). It is striking to find, therefore, that the spatial positioning of these loci differs drastically between the oriC@pole and oriC@midcell models. In the oriC@pole model (Figure 9C, upper panel), oriC is positioned close to the initiation-repressive datA, distant from the initiation-promoting DARS2 and with datA positioned between it and DARS2. In contrast, in the oriC@midcell model (Figure 9C, lower panel), oriC moves closer to DARS2 and positions itself directly between datA and DARS2. While these data are suggestive rather than conclusive, the relative spatial positions of oriC, datA and DARS2 are entirely consistent with the transition from the oriC@pole to the oriC@midcell chromosomal arrangement corresponding to a transition from a state repressive of further initiation events to a state primed for initiating replication (Figure 9D) (42).

CONCLUSION

The high resolution chromosome structures reported here enable a number of physical and genomic properties of the chromosome to be directly monitored in ways that would be impossible with lower resolution models. Examples of physical properties explored here include: (i) the distribution of void sizes within the nucleoid region—which have a direct bearing on the ease with which large macromolecular complexes can access the chromosomal interior—and (ii) the high frequency with which very close (<50 Å) contacts occur between genomically distant parts of the chromosome—which has obvious potential implications for search mechanisms of DNA-binding proteins. But perhaps more importantly, since every basepair of the E. coli chromosome is directly addressable in the models, the structures also provide putative but highly detailed views of the physical environment surrounding any genomic location of interest. Some possible but ambitious applications of the current models include: (i) simulating the long timescale dynamics of the chromosome in an attempt to reproduce the anomalous diffusion of chromosomal loci observed in vivo (74,86–88), (ii) simulating the spatial repositioning of genes that can accompany their activation (89) and (iii) modeling polysome-DNA segregation using methods similar to those pioneered by the Yethiraj and Weisshaar groups (20,21).

At the present stage of development, the models explicitly incorporate a wide variety of experimental restraints, but future iterations might also include higher-resolution contact information from techniques such as HiC (90), or incorporate recent data demonstrating the tendency of six of the seven ribosomal RNA operons to colocalize in rapidly-growing cells (91). Future models could also include sequence effects on local DNA structural features such as groove widths (92,93) and might explicitly model the sequence-specific binding of NAPs and their effects on DNA geometry. Accommodating the often-dramatic DNA bends that several of the NAPs introduce (54) is likely to be a substantial challenge, but work by the Olson group has already demonstrated the potential power of molecular simulations in describing the interplay between NAPs binding to DNA minicircles (94). It is not difficult to imagine that extending similar models to the chromosomal scale might lead to new insights.

Over the longer term, it might also be possible to extend the approach described here to explore the degree to which transcription affects, and is affected by, the local chromosomal environment (95) or to build detailed models of chromosomes in progressive stages of replication: the latter would, in turn, facilitate comparison with experimental data obtained under more rapid growth conditions. Regardless of what the next stages may be, we think that the construction of the models reported here provides a good illustration of the way that multi-resolution simulation methods can be profitably integrated with multiple sources of experimental data to generate detailed structures of macromolecules that might otherwise be impossible to obtain (96).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health (NIH) [R01 GM087290 to A.H.E]. Funding for open access charge: NIH [R01 GM087290].

Conflict of interest statement. None declared.