Abstract
The regulatory Community Multiscale Air Quality (CMAQ) model is a means to understanding the sources, concentrations and regulatory attainment of air pollutants within a model’s domain. Substantial resources are allocated to the evaluation of model performance. The Regionalized Air quality Model Performance (RAMP) method introduced here explores novel ways of visualizing and evaluating CMAQ model performance and errors for daily Particulate Matter ≤ 2.5 micrometers (PM2.5) concentrations across the continental United States. The RAMP method performs a non-homogenous, non-linear, non-homoscedastic model performance evaluation at each CMAQ grid. This work demonstrates that CMAQ model performance, for a well-documented 2001 regulatory episode, is non-homogeneous across space/time. The RAMP correction of systematic errors outperforms other model evaluation methods as demonstrated by a 22.1% reduction in Mean Square Error compared to a constant domain wide correction. The RAMP method is able to accurately reproduce simulated performance with a correlation of r = 76.1%. Most of the error coming from CMAQ is random error with only a minority of error being systematic. Areas of high systematic error are collocated with areas of high random error, implying both error types originate from similar sources. Therefore, addressing underlying causes of systematic error will have the added benefit of also addressing underlying causes of random error.
Keywords: model performance evaluation, regulatory modeling, PM2.5, CMAQ, modeled data
Graphical abstract
1. Introduction
Particulate Matter ≤ 2.5 micrometers in diameter (PM2.5) is one of the six “criteria air pollutants” regulated in the United States (Boldo et al., 2006; Pope et al., 2009) due to its association with adverse health effects, including cardiovascular and respiratory disease and mortality (Beelen et al., 2007; Krewski et al., 2009; Pope et al., 2004). The Community Multiscale Air Quality (CMAQ) model is used for regulatory purposes to assess attainment and estimate PM2.5 concentration. Substantial efforts are made to understand the model performance of CMAQ (Appel et al., 2013a, 2008; Carlton et al., 2010; Foley et al., 2015a, 2015b, 2010). Past work evaluating model performance typically gives modeling performance statistics over an aggregated level (e.g. monitoring locations, regions of the country, monitoring networks, etc.) (Simon et al., 2012). For the modeling domain the size of the continental United States, metrics are typically calculated for the Eastern versus Western US, urban stations versus rural stations, summer versus winter monitoring, etc. (Appel et al., 2013b). Displaying model performance metrics at each monitoring site location across the US reveals that CMAQ performance changes in a non-homogenous manner (Appel et al., 2012). However, model performance at a specific unmonitored space/time location is typically not explored. Therefore current methods fail to assess geographical or temporal changes of model performance across the spatiotemporal continuum, particularly in-between monitors.
The goal of this work is to address this significant knowledge gap by introducing a method that assesses model performance at any space/time region of interest across the spatiotemporal continuum. Advantages for assessing model performance at any region across a continuum include being able to 1) exactly delineate geographical patterns of modeling errors and 2) correct systematic errors across the modeling domain for individual CMAQ grid concentrations.
Systematic errors are consistent deviations of modeled data from observed data. Systematic errors, once assessed, can be used to correct the modeled value. The remaining error, i.e. the random noise of the modeled value around the observed data, is the random error. While current CMAQ model performance evaluation methods are multifaceted (Dennis et al., 2010) and use a wide array of metrics to quantify performance (Kang et al., 2007; Thunis et al., 2012; USEPA, 2005; Venkatram, 2008), this work specifically focuses on a set of metrics that investigate systematic and random errors. Hence, to achieve our goal, we introduce modeling error statistics that parse total error into systematic and random errors. Few studies have apportioned error in this manner (Solazzo and Galmarini, 2016).
The Regionalized Air quality Model Performance (RAMP) method introduced in this work assesses model performance across the spatiotemporal continuum of daily PM2.5 across the continental US. Our framework is a regionalized space/time extension of the Constant Air quality Model Performance (CAMP) method (de Nazelle et al., 2010) and parallels the work of Xu et al. (Xu et al., 2016). The CAMP method was originally created to account for the non-linear and non-homoscedastic relationship between modeled and observed ozone data in North Carolina for a particular ozone episode. The CAMP method assumes that model performance is homogenous across the state and does not change as a function of the space/time CMAQ grid locations. This assumption of homogeneity of model performance begins to break down as the modeling domain increases in size, particularly when this increase is substantial. The novel RAMP method introduced here for PM2.5 extends the CAMP method by accounting for the non-homogeneity of model performance in a regionalized fashion across the entirety of a modeling domain and fully characterizes the non-linear and non-homoscedastic relationship at any space/time region for any modeled value of interest.
This work demonstrates the use of the RAMP for daily PM2.5 mass predicted by CMAQ across the entirety of the continental United States. As an evaluation of the RAMP method, we have chosen a regulatory episode developed for the years 2001 and 2002. The model performance for this episode has been well documented and thus provides an ideal case study. The results of the RAMP analysis include maps showing the geographical variations of systematic and random errors displayed at the resolution of an individual CMAQ grid cell. These results provide new insights about model performance that complement existing performance evaluation methods. The RAMP results are helpful in making decision on resource allocation for further improvement in the air quality model. Furthermore, calculating systematic errors for individual CMAQ grids facilitate systematic error correction leading to maps of PM2.5 concentrations with improved mapping accuracy.
2. Materials and Methods
2.1 Observed and Modeled Data
Daily observed PM2.5 for each space/time location during 2000–2002 were constructed based on monitoring data from monitoring stations measuring either hourly or daily PM2.5 obtained from the EPA’s Air Quality Systems (AQS) data base (US EPA, 2011). Daily PM2.5 data were also constructed from CMAQ modeled data for years 2001 and 2002 using CMAQv4.5 across the contiguous United States on a 36 km grid. For more detailed information regarding the aggregation and pairing process of observed and modeled data see Supplementary data.
2.2 Variable Definition
Random variables X are in upper case and known values are in lower case. Let X̂(p) be the random variable representing the observed concentration at a single space/time location p = (s, t) where s is the spatial location and t is time, x̂(p) be its known value (i.e. realization) at space/time location p and x̃(p) be the CMAQ modeled value at space/time location p. The variable x̃(p) covers the entirety of the domain and is known everywhere. We define error as
| (Equ. 1) |
Error is defined as e(p) = x̃(p) − x̂(p) at locations where the observed data are known. The definition of error in this work is a deviation from what is typically used in the model performance literature. The differences in the nomenclature are explicitly stated in Supplementary data (Table A1 and Table A2).
2.3 Systematic and Random Error Statistics
In this work metrics are geared towards dividing error in a dichotomous manner. Namely, metrics are divided into systematic and random errors. Systematic errors are consistent errors between observed and modeled CMAQ data and can be removed through calculating the mean systematic error. Random errors are the residual errors remaining once the systematic error is removed. Random errors can be conceptualized as the random noise between CMAQ and observed data. Total error is the sum of the two. In the naming convention of a statistic the first letter(s) is used to identify the statistical operator as follows: M=mean, V=variance, S=Standard deviation, RMS=square Root of the Mean of Squared values. The last letter(s) is used to identify the value of interest as follows: E=Error (Equ. 1), SE=Squared Error=E2, S=Standardized error=E/σE, NE=Normalized Error=E/x̂ and . Statistics that are calculated over an entire domain 𝒟 are and . ME2(𝒟) quantifies the systematic error, VE(𝒟) quantifies the random error and MSE(𝒟) = ME2(𝒟) + VE(𝒟) quantifies the total error. The equations of systematic, random and total error can be represented pictorially in the Supplementary data (Fig. A1). Other statistics used in model performance evaluation include the square Root of the Mean of Squared Standardized errors (RMSS) and Mean of the square Root of variance (MR).
2.4 Constant Air quality Model Performance (CAMP)
The CAMP method (de Nazelle et al., 2010) performs a model performance analysis that accounts for the non-linearity and non-homoscedastic behavior of model performance with respect to the modeled value x̃k. The CAMP method does this by modeling the mean λ1 (x̃k; 𝒟) = M[X̂|x̃k; 𝒟] and variance λ2 (x̃k; 𝒟) = V[X̂|x̃k; 𝒟] of the observed value X̂ as function of a given model value x̃k across the domain 𝒟 using the equations
| (Equ. 2) |
| (Equ. 3) |
where n(x̃k; 𝒟) is the number of paired modeled x̃i and observed x̂i values across the space time domain 𝒟 such that x̃k − Δx̃ ≤ x̃i ≤ x̃k + Δx̃ where Δx̃ is a small tolerance corresponding to half of a decile of modeled values in 𝒟 around x̃i and it is assumed that x̂i ~ iid.
The CAMP method does not investigate how λ1 (x̃k; 𝒟) and λ2 (x̃k; 𝒟) change across the domain 𝒟.
2.5 Regionalized Air quality Model Performance (RAMP)
The Regionalized Air quality Model Performance (RAMP) method introduced here consists of extending the CAMP method (de Nazelle et al., 2010) by regionalizing the model performance to a space/time region ℛ(p) contained within 𝒟 associated with the space/time coordinate p. In this work the region ℛ(p) was selected such that it contains all paired modeled and observed data from the 3 closest stations within 180 days of p, visualized through a regionalized “S-curve” (Fig. 1). The 3 closest stations within 180 days were chosen for being as spatially specific as possible while still maintaining a stable pattern with the associated regionalized λ1 (x̃k; ℛ(p)) = M[X̂|x̃k; ℛ(p)] and λ2 (x̃k, ℛ(p)) = V[X̂|x̃k; ℛ(p)] parameters (see Supplementary data for S-curve parameter optimization). The regionalized parameters are defined as
| (Equ. 4) |
| (Equ. 5) |
where n(x̃k; ℛ(p)) is the number of paired modeled and observed points within ℛ(p) and around x̃k.
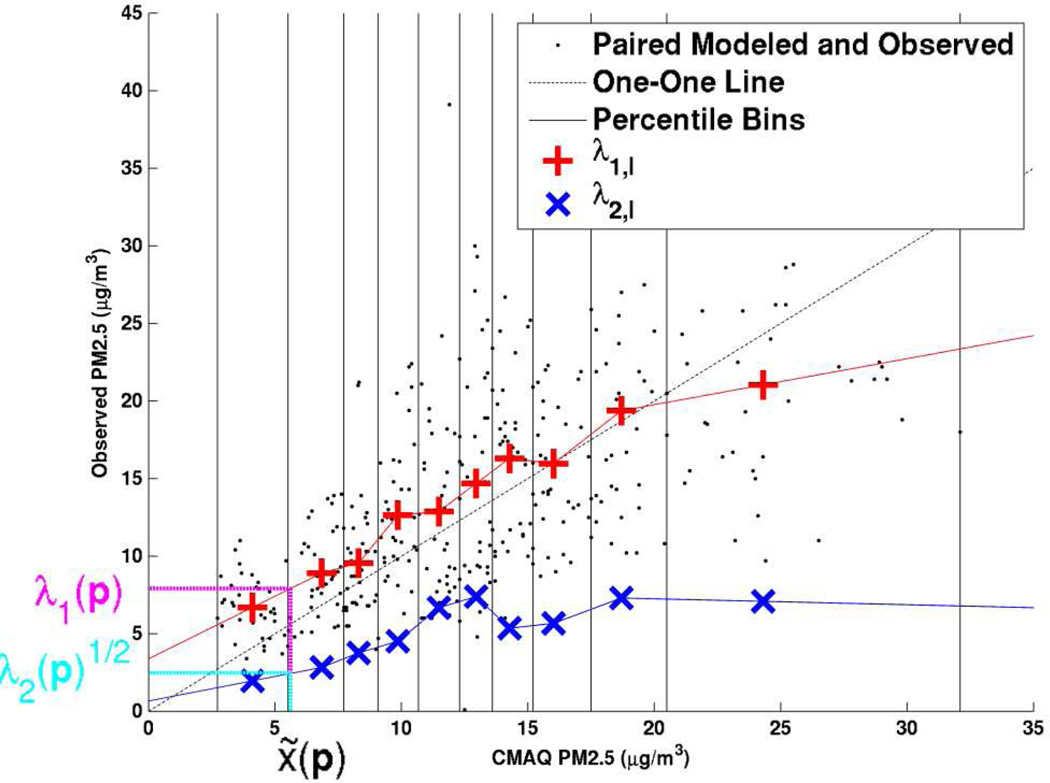
Figure 1.
RAMP analysis for an arbitrary CMAQ grid location on July 1, 2001 for daily PM2.5. The black dots are all the paired modeled and observed daily PM2.5 concentrations within a space/time region ℛ(p) consisting of the 3 closest stations to the CMAQ grid location of interest within 180 days of July 1, 2001, with modeled data on the independent axis and observed data on the dependent axis. The vertical black lines identify the 10 bins used to stratify all the paired data in which each bin contains one decile of all the paired points. The dotted black line is the one-to-one line between the modeled and observed data. The red + marker in each bin denotes λ1,l (x̃l, ℛ(p)), the average of paired observed values within the l-th decile bin. The blue × marker in each bin denotes the square root of λ2,l (x̃l; ℛ(p)), the standard deviation of paired observed values within that bin. As shown in the figure, the + and × markers are linearly interpolated to obtain the λ1 (p) and values, respectively, corresponding to the CMAQ modeled data x̃(p) within ℛ(p).
An efficient numerical implementation of the calculation of λ1 (x̃k; ℛ(p)) and λ2 (x̃k; ℛ(p)) is performed as follows. All modeled/observed (x̃i, x̂i) pairs within ℛ(p) are divided into deciles based off all the collected x̃i (Fig. 1). The mean and variance of observed values in each decile x̃l are calculated to obtain λ1,l (x̃l; ℛ(p)) and λ2,l (x̃l; ℛ(p)), respectively. A linear interpolation between deciles is performed to obtain λ1 (x̃k; ℛ(p)) and λ2 (x̃k; ℛ(p)). If the S-curve contains less than 150 pairs, points from the nearest stations are pulled in until at least 150 pairs are obtained. When calculating the variance of the error correction of the modeled data (Equ. 5), it is assumed x̂i ~ iid. Thus, λ1 (x̃k; ℛ(p)) and λ2 (x̃k; ℛ(p)) describe the mean and variance of observed concentration as a function of both x̃k and the space/time region ℛ(p). For example, in Fig. 1 for the given ℛ(p) and x̃k = 5.6 µg/m3, λ1 (x̃k; ℛ(p)) = 7.9 µg/m3 and . Other S-curves are visualized in Supplemental data.
There is a correspondence between the parameters λ1 (x̃k; ℛ(p)) and λ2 (x̃k; ℛ(p)) and systematic and random errors. From Equ. 1 we have X̂ = x̃ − E, which, once substituted into λ1 (x̃k; ℛ(p)) and λ2 (x̃k, ℛ(p)) yields
| (Equ. 6) |
| (Equ. 7) |
where ME(x̃k; ℛ(p)) and VE(x̃k; ℛ(p)) are the mean and variance, respectively, of the error associated with an arbitrary value x̃k predicted within region ℛ(p).
We also define and as the mean and variance of observed concentration when x̃k = x̃(p), where x̃(p) is the CMAQ modeled value at p. By replacing x̃k with x̃(p) in Equ. 6 and Equ. 7, we obtain
| (Equ. 8) |
| (Equ. 9) |
Equ. 8 and Equ. 9 provide a physical interpretation of systematic and random errors. The systematic error ME(x̃(p); ℛ(p)) is the error correction that can be applied to the modeled value x̃(p) in region ℛ(p) to produce a corrected modeled estimate , and the random error quantified by VE(x̃(p); ℛ(p)) characterizes the residual uncertainty associated with the systematic error corrected modeled estimate. In this work ME(x̃(p); ℛ(p)) and VE(x̃(p); ℛ(p)) can be approximated by and , respectively, where for a given p, n(p) is equal to the number of paired modeled and observed points in ℛ(p).
The RAMP method provides the statistical distribution of observed air pollution as
| (Equ. 10) |
where and are the mean and variance of observed values given the modeled value x̃(p), but is flexible enough to accommodate other distributions. In short, the RAMP method 1) calculates the sample mean and sample variance of the observed data that are contained within a given region R(p) and close in value to the CMAQ concentration x̃(p) through the parameters and , 2) equates and with systematic and random error parameters ME(x̃(p), R(p)) and VE(x̃(p), R(p)) and 3) adjusts the CMAQ value and with a corresponding uncertainty through the parameters and .
2.6 Validation and Stochastic Simulation
Validation is performed by comparing the accuracy of the model correction performed by three approaches: the Constant, CAMP and RAMP correction methods. The Constant correction method is defined through
| (Equ. 11) |
with associated error variance
| (Equ. 12) |
i.e. the correction ME(𝒟) and its associated error variance VE(𝒟) are constant across the entirety of the domain with respect to both modeled value x̃k and location p. The CAMP method assumes that the model performance of CMAQ is represented by a domain wide S-curve λ1 (x̃k; 𝒟) and λ2 (x̃k; 𝒟) (Equ. 2, 3) that are a function of the modeled value x̃k, but not a function of space/time location p. In the CAMP method the correction for x̃(p) is performed by substituting x̃k with x̃(p) in the domain-wide S-curve, i.e. using the correction
| (Equ. 13) |
with associated error variance
| (Equ. 14) |
The RAMP correction on the other hand is done using Equ. 8 and 9. The corrected λ1 (p) values for the Constant (Equ. 11), CAMP (Equ. 13) and RAMP (Equ. 8) methods are compared by calculating performance statistics between paired λ1 (p) and x̂(p) values for 2001. The performance of λ2 (p) is assessed through standardized errors (i.e. ).
We also conduct a stochastic simulation to test how well each method reproduces the simulated values. The maps of λ1 (p) and λ2 (p) obtained in this work are defined as being the true mean and variance of observed values. We also select x̃(p) from this work as being the true modeled value. We randomly generate x̂*(p) ~ N(λ1 (p), λ2 (p)) and then we re-calculate λ1*(p) and λ2*(p) using the Constant, CAMP and RAMP methods based only on paired x̃(p) and x̂*(p). Lastly, λ1*(p) and λ2*(p) are compared with λ1 (p) and λ2 (p) visually through maps and through statistical metrics to evaluate how well λ1*(p) and λ2*(p) are able to capture the spatial variability in the true mean, λ1 (p), and variance, λ2 (p), of observed values.
3. Results and Discussion
3.1 Model Performance Evaluation Demonstrating Results of the RAMP Analysis
A demonstration of the RAMP method was performed using daily PM2.5 concentrations predicted by CMAQv4.5 at the 36 km grid level for 2001 across the continental United States. CMAQv4.5 is the most recent version available for 2001 across the continental US. Although newer versions of CMAQ exist for later years, it was critical to analyze model performance in 2001 due to an ongoing epidemiological study focused on novel neurodegenerative PM2.5 health end points and its association with loss of brain mass in older women (Casanova et al., 2016; Chen et al., 2015). From an epidemiologic perspective, a model performance evaluation that can distinguish systematic from random error is especially important for a model version with known deficiencies (Foley et al., 2010). This information can inform subsequent error correction of systematic errors and data fusion methods.
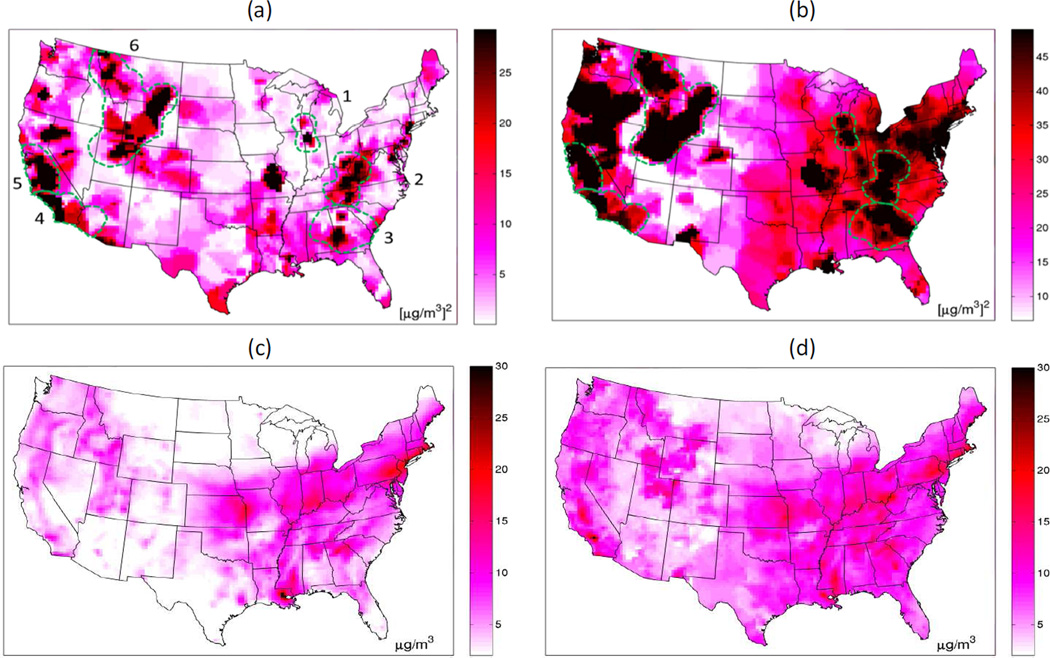
Results of the RAMP analysis can be visualized for July 1, 2001 (Fig. 2). The RAMP results indicate that there are geographical patterns in ME2(p) = ME2(x̃(p); ℛ(p)) (Fig. 2a) and VE(p) = VE(x̃(p); ℛ(p)) (Fig. 2b). This indicates that both systematic errors and random errors are non-homogenous as demonstrated by the > 10 fold variation in ME2(p) and VE(p) across the continental United States on that day. The maps shown in Fig. 2a–b allow for the identification of regions with high systematic and random errors. This is critical information needed to better understand the spatial uncertainty of model performance of the CMAQ predicted values x̃(p) across a given day (Fig. 2c). The RAMP analysis also produces (Fig. 2d). In addition to the results shown in Fig. 2, the RAMP analysis produces a rich set of more detailed model performance metrics (see Supplementary data).
Figure 2.
Maps of RAMP error and RAMP error correction of CMAQ. Daily PM2.5 across the continental United States on July 1, 2001 displaying (a) RAMP ME2(p), (b) RAMP VE(p), (c) CMAQ concentration x̃(p) and (d) . Plots (c) and (d) are in µg/m3 and (a) and (b) are in (µg/m3)2. Plot (b) shows 6 regions of large random error delineated in the dashed green line with the same regions delineated and labeled in (a). Delineated regions include (1) the Great Lakes, (2) the Appalachian Mountains, (3) the South East, (4) Southern California, (5) Northern California and (6) the Rocky Mountains.
The domain wide model performance of CMAQ is assessed by the performance statistics ME(𝒟), , MSE(𝒟) and r(𝒟) calculated over a domain 𝒟 corresponding to the continental United States in 2001. These statistics are shown in the first column of Table 1. Due to the influential nature of highly skewed standardized errors, all data were removed whose standardized errors were either less than the 0.1 percentile or greater than the 99.9 percentile, constituting 348 data points. As shown in Table 1, the mean error for CMAQ is ME(𝒟) = −1.05 (µg/m3), indicating that CMAQv4.5 has systematic errors that underestimates PM2.5 by 1.05 µg/m3 across the continental United States in 2001 on average. Interestingly, , indicating that random errors are much larger than systematic errors. These systematic and random errors result in a total error of MSE(𝒟) = 61.5 (µg/m3)2 and a precision quantified by a correlation r(𝒟) = 0.589 between observed and modeled values.
Table 1.
Validation statistics. Statistics of the validation results of daily paired observed PM2.5 and λ1 (p) and λ2 (p) estimated from each of the three methods: the Constant method, CAMP and RAMP for 2001 across the continental United States. The CMAQ column are the statistics between the paired observed and CMAQ concentrations. VS is variance of the standardized errors, RMSS is square root of the mean squared standardized errors and MR is the mean of the square root of λ2 (p).
| Statistic | CMAQ | CMAQ Corrected | ||
|---|---|---|---|---|
| Constant Correction |
Non-linear/Non homoscedastic (CAMP) Correction |
Non-linear/Non homoscedastic and Non-homogenous (RAMP) Correction |
||
| ME(𝒟) (µg/m3) | −1.05 | 0.0304 | 0.0281 | −0.0202 |
| (µg/m3) | 7.77 | 7.18 | 6.58 | 6.34 |
| MSE(𝒟) (µg/m3)2 | 61.5 | 51.5 | 43.3 | 40.1 |
| r(𝒟) (unitless) | 0.589 | 0.625 | 0.631 | 0.698 |
| VS(𝒟) (unitless) | -- | 0.766 | 0.823 | 1.05 |
| RMSS(𝒟) (unitless) | -- | 0.875 | 0.907 | 1.03 |
| MR(𝒟) (µg/m3) | -- | 8.20 | 7.04 | 5.45 |
3.2 Validation Results
The validation statistics of three model performance evaluation methods (Constant, CAMP and RAMP) are shown in Table 1. These methods have different assumptions. The Constant method assumes that model performance is constant across 𝒟, the CAMP method accounts for non-linear and non-homoscedastic model performance and the RAMP method accounts for non-linear, non-homoscedastic and non-homogeneous model performance. The validation statistics are calculated using a corrected CMAQ value λ1 (p) and associated error variance λ2 (p) given by (Equ. 11, 12), (Equ. 13, 14), and (Equ. 8, 9) for the Constant, CAMP and RAMP methods, respectively.
Validation of λ1 (p) is performed by comparing the ME(𝒟), , MSE(𝒟) and r(𝒟) performance statistics of the raw CMAQ estimate (the first column of Table 1) with λ1 (p) for each of the three performance evaluation methods (the last three columns of Table 1). The magnitude of ME(𝒟) drops from −1.05 (µg/m3) for CMAQ to 0.0304 (µg/m3), 0.0281 (µg/m3) and −0.0202 (µg/m3) for the Constant, CAMP and RAMP methods, respectively. This was expected by design due to each method eliminating systematic errors across 𝒟. The model performance evaluation methods differ in their abilities to reduce random errors, as demonstrated by the statistic. The statistic progressively reduces from 7.77 (µg/m3) for CMAQ to 7.18 (µg/m3), 6.58 (µg/m3) and 6.34 (µg/m3) for the Constant, CAMP and RAMP methods, respectively. This translates in a total error that is lower for RAMP (MSE = 40.1 (µg/m3)2) than for CAMP (MSE = 43.3 (µg/m3)2) and the Constant method (MSE = 51.5(µg/m3)2). This corresponds to a 22.1% reduction in MSE from the Constant to the RAMP method. This finding is further confirmed by the correlation between observed and λ1 (p) values, which progressively increases from r = 0.589 for CMAQ to r = 0.698 for RAMP. These results demonstrate that λ1 (p) calculated by the RAMP method is more accurate than the raw CMAQ output or the CMAQ corrected values obtained from the other model performance evaluation methods.
Validation of λ2 (p) is performed by comparing the VS(𝒟), RMSS(𝒟) and MR(𝒟) performance statistics across the different model performance evaluation methods. The VS and RMSS are the variance and root mean squared error, respectively, of the Standardized error S, where for the Constant method and for the CAMP and RAMP methods. The standardized errors should ideally have a standard normal distribution, hence VS and RMSS should ideally be 1. VS is 0.766 for the Constant method, 0.823 for the CAMP method and 1.05 for the RAMP method. The RAMP λ2 (p) is more accurate than the Constant or CAMP λ2 (p). The VS for the Constant method and CAMP, being less than one, overestimate the CMAQ prediction error variance. This result is confirmed by the RMSS and is further quantified by the MR. The MR is the mean of the CMAQ prediction error standard deviations. The MR(𝒟) for RAMP indicates that the random error of CMAQ prediction has a standard deviation of 5.45 µg/m3 across 𝒟 on average. The MR(𝒟) for the Constant method is 8.20 µg/m3, indicating that the Constant method leads to a substantial overestimation of random errors by 50.5% over RAMP estimates. The overestimation of random error is attenuated with the CAMP method, which has an MR(𝒟) equal to 70.4 µg/m3 corresponding to a 29.2% overestimation compared to the RAMP estimates.
Overall these validation results demonstrate that the RAMP method provides a λ1 (p) value that better corrects systematic errors than other performance evaluation methods and provides a λ2 (p) value that better estimates random errors compared to other model performance evaluation methods. We hypothesize that this is due to the RAMP method being better able to assess the spatial and temporal uncertainty of systematic and random errors compared with other model performance evaluation methods.
3.3 Stochastic Simulation Results
The map of the true systematic error x̂(p) − λ1 (p) for July 1, 2001 displays by design clear geographical trends identifying well defined regions where systematic error is large (Supplementary data). The map of re-calculated systematic error x̂(p) − λ1*(p) obtained using the Constant method is constant and is therefore unable to capture the spatial variability in systematic errors. The corresponding map obtained with the CAMP method is able to capture spatial variability occurring across the entire modeling domain, but unable to capture the regional and fine scale variability in systematic errors. However, the corresponding RAMP map captures spatial variability of systematic errors at a fine spatial scale. The correlation coefficient r calculated between x̂(p) − λ1 (p) and x̂(p) − λ1*(p) for July 1, 2001 is 0.0%, 24.0% and 76.1% for the Constant, CAMP and RAMP methods, respectively. These results demonstrate that the RAMP method is better able to capture fine scale spatial variability of systematic errors.
Similar results were found when comparing the true λ2 (p) with λ2*(p) obtained for each model performance evaluation method, again for July 1, 2001. Qualitatively, the λ2*(p) map obtained with the Constant method misrepresents the true λ2 (p) map by failing to capture any of the spatial variability in random errors and overestimating the average random error. The λ2*(p) map obtained with the CAMP method is a considerable improvement by reproducing variability at a long scale distance. However, visually, the CAMP method is unable to capture fine scale variability. The λ2*(p) map obtained with the RAMP method provides a good visual reproduction of the true random error. These results are quantitatively supported by the correlation coefficient between λ2 (p) and λ2*(p) of 0.0%, 5.18% and 54.5% for the Constant, CAMP and RAMP methods, respectively.
These results demonstrate that in situations where there is regional variability in model performance, the RAMP method is better able to estimate the spatial variability of systematic errors compared to the Constant and CAMP methods. This implies the RAMP method should be considered for performance evaluation in future studies when it is plausible for model performance to vary spatially.
3.4 Evidence and Implications of Non-Linear and Non-Homoscedastic Model Performance
This work contributes novel evidence that the performance of air quality models is non-linear and non-homoscedastic. That is, λ1 and λ2 are a non-linear function of the modeled value x̃k. This is seen through 1) the comparison of the Constant method and the CAMP method and 2) the stochastic simulation results. The Constant method assumes that λ1 − x̃k and λ2 do not vary as a function of x̃k. The CAMP method assumes that λ1 and λ2 are non-linear functions of x̃k. The first evidence of non-linear and non-homoscedastic behavior comes from the validation results. The MSE reduces from 51.5 (µg/m3)2 for the Constant method to 43.3 (µg/m3)2 for the CAMP method, corresponding to a 16% reduction in MSE that demonstrates that model performance improves for a non-linear and non-homoscedastic model. In the stochastic simulation results, the Constant method is unable to capture the spatial variability in systematic and random errors whereas the CAMP method is able to capture domain-wide variability of these errors. Furthermore, both the validation and stochastic simulation results indicate that the Constant method significantly over predicts random errors compared to the CAMP method. Finally, the non-homoscedastic behavior in model performance is evidenced by maps of λ2 (x̃k; ℛ(p)) for different fixed x̃k values (see Supplementary data), showing that the error variance changes substantially from one value of x̃k to another for a given region ℛ(p).
From these results, one should be cautious when using linear and homoscedastic model performance evaluation methods to explore the spatial variability of model performance. This is the usual practice of current approaches in which models can be expressed as X̃(s) = β0(s) + β1(s)X̂(s) + ε(s) (Fuentes and Raftery, 2005) or X̂(s, t) = β0(s, t) + β1(s, t)x̃(s, t) + ε(s, t) (Berrocal et al., 2010). In both cases the relationship is linear and homoscedastic when assuming a constant error variance of the noise term (i.e. ). This may undermine their capacity to fully capture spatial variability in model performance. Furthermore, these methods may overestimate the error variance. By contrast the RAMP method provides a novel alternative that fully captures the space/time variability of non-linear, non homoscedastic model performance and, as a result, provides a novel description of the spatial patterns in systematic and random errors across the spatiotemporal continuum.
3.5 Spatial Patterns of Systematic and Random Errors
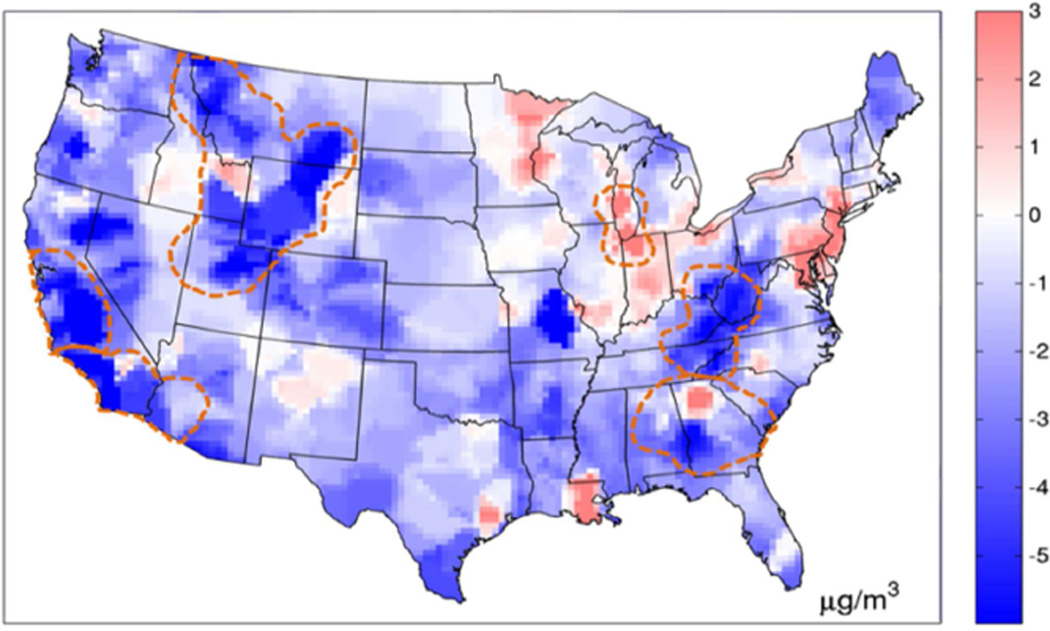
To better understand the magnitude of the systematic errors ME2(p) (Fig. 2a), we also show a map of ME(p) (Fig. 3), which differentiates areas where daily PM2.5 concentrations are over predicted (i.e. ME > 0) versus under predicted (i.e. ME < 0). The map of ME(p) is in line with known CMAQ deficiencies. That is, CMAQ generally struggles with estimating high values of PM2.5 (Yu et al., 2012, 2008). Areas shown with negative ME(p) values in Fig. 3 (i.e. where PM2.5 is under predicted) coincide with areas shown to have high λ1 (p) values in Fig. 2d (i.e. where PM2.5 levels are high).
Figure 3.
Map of RAMP mean error. Daily PM2.5 across the continental United States on July 1, 2001 displaying ME(p) in µg/m3. The 6 regions of high random error delineated in Fig. 2b are delineated in the dashed orange line.
The RAMP analysis provides a map of ME2(p) across the continuous space/time domain (as opposed to being restricted to only monitoring stations). This makes it possible to clearly delineate and identify specific regions with high ME2(p) values and quantify their geographical extent. To illustrate this capability, we identified in regions (labeled 1–6 in Fig. 2a) defined as having relatively high systematic error (i.e. ME2(p) ≥ 17.4 (µg/m3)2). The areas of high systematic error are quantified as follows: (1) the Great Lakes (15,552 km2), (2) the Appalachian Mountains (116,640 km2), (3) the South East (38,880 km2), (4) Southern California (73,872 km2), (5) Northern California (75,168 km2) and (6) the Rocky Mountains (290,304 km2).
Some of the regions identified for their high systematic errors are corroborated in the literature. The over prediction in region 1 (the Great Lakes) is in line with an overestimation of residential wood burning in the region reported in the National Emissions Inventory (NEI) (Appel et al., 2008). Region 3 (South East) includes Atlanta where PM2.5 is over estimated and an area to its South where PM2.5 is under estimated. CMAQ is known to under predict PM in the South East. Some of this under prediction may be associated with highly uncertain SOA chemistry, particularly including chemistry from biogenic emissions (Chan et al., 2010; Morris et al., 2006). Likewise high systematic error in the mountain regions 2 and 6 (Appalachia Mountains and the Rockies) can be associated with the known difficulties in modeling air quality accurately on and near mountain ranges (Steyn et al., 2013). The causes of high systematic error identified by RAMP may not be well documented in other regions. For example, the identification of Northern California (region 4) and Southern California (region 5) may serve as a trigger for further investigation into the constituents and chemical pathways of PM2.5 (Motallebi et al., 2003; USEPA, 2001) to investigate causes that may lead to systematic errors in these areas. To our knowledge this is the first work in the model performance literature to delineate these regions and quantify their geographic extent.
The map of VE(p) in Fig. 2b delineates areas with high random errors. It is interesting to note that areas of high systematic errors are always fully contained within areas of high random error as seen by comparing Fig. 2a and Fig. 2b. To our knowledge these are the first maps delineating regions of high random errors and finding general collocation with (and about twice the magnitude of) systematic errors. If both systematic and random errors are caused by similar processes, then reducing systematic errors could have the added benefit of also addressing collocated random errors.
4. Conclusions
This work introduces a spatiotemporal approach that can estimate and distinguish systematic error from random error of predictions made by regulatory air quality models at any location within a given modeling domain. The estimation of systematic and random errors is created in a manner that does not assume that the relationship between observed and modeled values is linear or homoscedastic, and estimation of errors is performed in a manner that is regionalized. By estimating errors across a continuous geographical domain for a given day of interest, this approach permits the production of maps delineating areas of high errors. These maps are useful to 1) assess model performance by quantifying systematic and random errors at a fine spatial resolution across the entire space/time domain where monitoring does not exist and 2) do a model correction of systematic errors of the CMAQv4.5 estimates of PM2.5 for 2001 for individual grids. Future works include performing a data fusion of RAMP model corrected values and observations using the geostatistical Bayesian Maximum Entropy (BME) method of PM2.5 (Akita et al., 2012; Allshouse et al., 2009; de Nazelle et al., 2010; Reyes and Serre, 2014; Xu et al., 2016), for increased prediction accuracy, and updating the RAMP analysis for other years. This future work will be critical for ongoing epidemiologic studies analyzing the effect of air pollution on brain aging for women in the Women’s Health Initiative-Memory Study who were exposed to air pollution between 1999 and 2006 (Casanova et al., 2016; Chen et al., 2015). The application of RAMP on CMAQv4.5 demonstrated that the RAMP analysis was able to successfully identify known regions of errors of this version of CMAQ. This work provides a model correction for 2001 based on the most recent of CMAQ for this year and provides a useful baseline against which future versions can be compared to explore changes in systematic and random errors.
Supplementary Material
Highlights.
Error correction performed for individual CMAQ grids
Maps created showing model performance at unmonitored locations
Most error coming from CMAQ is random error
There is a need to evaluate model performance in a regionalized manner
Acknowledgments
This research was supported in part by the National Institute on Aging (NIA) under award number R01AG033078, the National Institute of Occupational Safety and Health (NIOSH) under grant 2T42/OH-008673 and the National Institute of Environmental Health Sciences (NIEHS) under grant T32ES007018. CMAQ modeling was performed by the US EPA. This research has not been formally reviewed by the EPA. The views expressed in this document are solely those of the authors and do not necessarily reflect those of the NIA, NIOSH, NIEHS or the EPA.
References
- Akita Y, Chen J-C, Serre ML. The moving-window Bayesian maximum entropy framework: estimation of PM2.5 yearly average concentration across the contiguous United States. J. Expo. Sci. Environ. Epidemiol. 2012;22:496–501. doi: 10.1038/jes.2012.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allshouse WB, Pleil JD, Rappaport SM, Serre ML. Mass fraction spatiotemporal geostatistics and its application to map atmospheric polycyclic aromatic hydrocarbons after 9/11. Stoch. Environ. Res. Risk Assess. 2009;23:1213–1223. [Google Scholar]
- Appel KW, Bhave PV, Gilliland AB, Sarwar G, Roselle SJ. Evaluation of the community multiscale air quality (CMAQ) model version 4.5: Sensitivities impacting model performance; Part II—particulate matter. Atmos. Environ. 2008;42:6057–6066. [Google Scholar]
- Appel KW, Chemel C, Roselle SJ, Francis XV, Hu RM, Sokhi RS, Rao ST, Galmarini S. Examination of the Community Multiscale Air Quality (CMAQ) model performance over the North American and European domains. Atmos. Environ. 2012;53:142–155. [Google Scholar]
- Appel KW, Pouliot GA, Simon H, Sarwar G, Pye HOT, Napelenok SL, Akhtar F, Roselle SJ. Evaluation of dust and trace metal estimates from the Community Multiscale Air Quality (CMAQ) model version 5.0. Geosci. Model Dev. 2013a;6:883–899. [Google Scholar]
- Appel KW, Pouliot GA, Simon H, Sarwar G, Pye HOT, Napelenok SL, Akhtar F, Roselle SJ. Evaluation of dust and trace metal estimates from the Community Multiscale Air Quality (CMAQ) model version 5.0. Geosci. Model Dev. Discuss. 2013b;6:1859–1899. [Google Scholar]
- Beelen R, Hoek G, Fischer P, van den Brandt PA, Brunekreef B. Estimated long-term outdoor air pollution concentrations in a cohort study. Atmos. Environ. 2007;41:1343–1358. [Google Scholar]
- Berrocal VJ, Gelfand AE, Holland DM. A Bivariate Space-Time Downscaler Under Space and Time Misalignment. Annu. Appl. Stat. 2010;4:1942–1975. doi: 10.1214/10-aoas351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boldo E, Medina S, LeTertre A, Hurley F, Mücke HG, Ballester F, Aguilera I, Eilstein D. Apheis: Health impact assessment of long-term exposure to PM2.5 in 23 European cities. Eur. J. Epidemiol. 2006;21:449–458. doi: 10.1007/s10654-006-9014-0. [DOI] [PubMed] [Google Scholar]
- Carlton AG, Bhave PV, Napelenok SL, Edney EO, Sarwar G, Pinder RW, Pouliot GA, Houyoux M. Model representation of secondary organic aerosol in CMAQv4.7. Environ. Sci. Technol. 2010;44:8553–8560. doi: 10.1021/es100636q. [DOI] [PubMed] [Google Scholar]
- Casanova R, Wang X, Reyes J, Akita Y, Serre ML, Vizuete W, Chui HC, Driscoll I, Resnick SM, Espeland MA, Chen J-C. A voxel-based morphometry study reveals local brain structural alterations associated with ambient fine particles in older women. Front. Hum. Neurosci. 2016;10:495. doi: 10.3389/fnhum.2016.00495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan MN, Surratt JD, Claeys M, Edgerton ES, Tanner RL, Shaw SL, Zheng M, Knipping EM, Eddingsaas NC, Wennberg PO, Seinfeld JH. Characterization and Quantification of Isoprene-Derived Epoxydiols in Ambient Aerosol in the Southeastern United States. Environ. Sci. Technol. 2010;44:4590–4596. doi: 10.1021/es100596b. [DOI] [PubMed] [Google Scholar]
- Chen J-C, Wang X, Wellenius Ga, Serre ML, Driscoll I, Casanova R, McArdle JJ, Manson JE, Chui HC, Espeland Ma. Ambient air pollution and neurotoxicity on brain structure: evidence from Women’s Health Initiative Memory Study. Ann. Neurol. 2015;78:466–476. doi: 10.1002/ana.24460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Nazelle A, Arunachalam S, Serre ML. Bayesian Maximum Entropy integration of ozone observations and model predictions: An application for attainment demonstration in North Carolina. Environ. Sci. Technol. 2010;44:5707–5713. doi: 10.1021/es100228w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennis R, Fox T, Fuentes M, Gilliland A, Hanna S, Hogrefe C, Irwin J, Rao ST, Scheffe R, Schere K, Steyn D, Venkatram A. A framework for evaluating regional-scale numerical photochemical modeling systems. Environ. Fluid Mech. 2010;10:471–489. doi: 10.1007/s10652-009-9163-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foley KM, Dolwick P, Hogrefe C, Simon H, Timin B, Possiel N. Dynamic evaluation of CMAQ part II: Evaluation of relative response factor metrics for ozone attainment demonstrations. Atmos. Environ. 2015a;103:188–195. [Google Scholar]
- Foley KM, Hogrefe C, Pouliot G, Possiel N, Roselle SJ, Simon H, Timin B. Dynamic evaluation of CMAQ part I: Separating the effects of changing emissions and changing meteorology on ozone levels between 2002 and 2005 in the eastern US. Atmos. Environ. 2015b;103:247–255. [Google Scholar]
- Foley KM, Roselle SJ, Appel KW, Bhave PV, Pleim JE, Otte TL, Mathur R, Sarwar G, Young JO, Gilliam RC, Nolte CG, Kelly JT, Gilliland aB, Bash JO. Incremental testing of the Community Multiscale Air Quality (CMAQ) modeling system version 4.7. Geosci. Model Dev. 2010;3:205–226. [Google Scholar]
- Fuentes M, Raftery AE. Model evaluation and spatial interpolation by Bayesian combination of observations with outputs from numerical models. Biometrics. 2005;61:36–45. doi: 10.1111/j.0006-341X.2005.030821.x. [DOI] [PubMed] [Google Scholar]
- Kang D, Mathur R, Schere K, Yu S, Eder B. New categorical metrics for air quality model evaluation. J. Appl. Meteorol. Climatol. 2007;46:549–555. [Google Scholar]
- Krewski D, Jerrett M, Burnett RT, Ma R, Hughes E, Shi Y, Turner MC, Pope CA, Thurston G, Calle EE, Thun MJ. Extended follow-up and spatial analysis of the American Cancer Society study linking particulate air pollution and mortality. Respir. Rep Heal. Eff. Inst. 2009;140:5–114. [PubMed] [Google Scholar]
- Morris RE, Koo B, Guenther A, Yarwood G, McNally D, Tesche TW, Tonnesen G, Boylan J, Brewer P. Model sensitivity evaluation for organic carbon using two multi-pollutant air quality models that simulate regional haze in the southeastern United States. Atmos. Environ. 2006;40:4960–4972. [Google Scholar]
- Motallebi N, Taylor CA, Jr, Croes BE. Particulate matter in California: Part 2-Spatial, temporal, and compositional patterns of PM2.5, PM10-2.5, and PM10. J. Air Waste Manage. Assoc. 2003;53:1517–1530. doi: 10.1080/10473289.2003.10466323. [DOI] [PubMed] [Google Scholar]
- Pope CA, Burnett RT, Thurston GD, Thun MJ, Calle EE, Krewski D, Godleski JJ. Cardiovascular Mortality and long-term exposure to particulate air pollution: Epidemiological evidence of general pathophysiological pathways of disease. Circulation. 2004;109:71–77. doi: 10.1161/01.CIR.0000108927.80044.7F. [DOI] [PubMed] [Google Scholar]
- Pope CA, Ezzati M, Dockery DW. Fine-particulate air pollution and life expectancy in the United States. N. Engl. J. Med. 2009;360:376–386. doi: 10.1056/NEJMsa0805646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes JM, Serre ML. An LUR/BME framework to estimate PM2.5 explained by on road mobile and stationary sources. Environ. Sci. Technol. 2014;48:1736–1744. doi: 10.1021/es4040528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon H, Baker KR, Phillips S. Compilation and interpretation of photochemical model performance statistics published between 2006 and 2012. Atmos. Environ. 2012;61:124–139. [Google Scholar]
- Solazzo E, Galmarini S. Error apportionment for atmospheric chemistry-transport models: a new approach to model evaluation. Atmos. Chem. Phys. Discuss. 2016:1–39. [Google Scholar]
- Steyn DG, de Wekker SFJ, Kossmann M, Martilli A. Boundary Layers and Air Quality in Mountainous Terrain. In: Chow FK, de Wekker SFJ, Snyder BJ, editors. Mountain Weather Research and Forecasting. Springer Netherlands: 2013. pp. 219–260. [Google Scholar]
- Thunis P, Pederzoli A, Pernigotti D. Performance criteria to evaluate air quality modeling applications. Atmos. Environ. 2012;59:476–482. [Google Scholar]
- US EPA. Air Quality System (AQS) [WWW Document] [accessed 9.11.10];2011 URL http://www.epa.gov/ttn/airs/airsaqs/
- USEPA. CMAQ Model Performance Evaluation for 2001: Updated March 2005, annual report. 2005 [Google Scholar]
- USEPA. Research Triangle Park, NC: 2001. National Air Quality and Emission Trends Report, 1999. [Google Scholar]
- Venkatram A. Computing and displaying model performance statistics. Atmos. Environ. 2008;42:6862–6868. [Google Scholar]
- Xu Y, Serre ML, Reyes JM, Vizuete W. Bayesian Maximum Entropy integration of ozone observations and model predictions: A national application. Environ. Sci. Technol. 2016;50:4393–4400. doi: 10.1021/acs.est.6b00096. [DOI] [PubMed] [Google Scholar]
- Yu S, Mathur R, Pleim J, Pouliot G, Wong D, Eder B, Schere K, Gilliam R, Rao ST. Comparative evaluation of the impact of WRF/NMM and WRF/ARW meteorology on CMAQ simulations for PM 2.5 and its related precursors during the 2006 TexAQS/GoMACCS study. Atmos. Chem. Phys. 2012;12:4091–4106. [Google Scholar]
- Yu S, Mathur R, Schere K, Kang D, Pleim J, Young J, Tong D, Pouliot G, Mckeen SA, Rao ST. Evaluation of real-time PM 2.5 forecasts and process analysis for PM 2.5 formation over the eastern United States using the Eta-CMAQ forecast model during the 2004 ICARTT study. J. Geophys. Res. 2008;113 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.