Validation of a Cardiovascular Disease Policy Micro-simulation Model Using Both Survival and Receiver Operating Characteristic Curves

Abstract

Background

Despite some advances, cardiovascular disease (CVD) remains the leading cause of death and healthcare costs in the U.S. We therefore developed a comprehensive CVD policy simulation model that identifies cost-effective approaches for reducing CVD burden. This paper aims to: 1) describe our model in detail; and 2) perform model validation analyses.

Methods

The model simulates 1,000,000 adults (ages 35–80 years) using a variety of CVD-related epidemiological data, including previously calibrated Framingham-based risk scores for coronary heart disease and stroke. We validated our micro-simulation model using recent National Health and Nutrition Examination Survey (NHANES) data, with baseline values collected in 1999–2000 and cause-specific mortality follow-up through 2011. Model-based (simulated) results were compared to observed all-cause and CVD-specific mortality data (from NHANES) for the same starting population using survival curves and, in a method not typically used for disease model validation, receiver operating characteristic (ROC) curves.

Results

Observed 10-year all-cause mortality in NHANES versus the simulation model were 11.2% (95% CI: 10.3–12.2%) versus 10.9%; corresponding results for CVD mortality were 2.2% (1.8–2.7%) versus 2.6%. Areas under the ROC curves for model-predicted 10-year all-cause and CVD mortality risks were 0.83 (0.81–0.85) and 0.84 (0.81–0.88), respectively; corresponding results for 5-year risks were 0.80 (0.77–0.83) and 0.81 (0.75–0.87), respectively.

Limitations

The model is limited by the uncertainties in the data used to estimate its input parameters. Additionally, our validation analyses did not include non-fatal CVD outcomes due to NHANES data limitations.

Conclusions

The simulation model performed well in matching to observed nationally representative longitudinal mortality data. ROC curve analysis, which has been traditionally used for risk prediction models, can also be used to assess discrimination for disease simulation models.

INTRODUCTION

Cardiovascular disease (CVD) continues to be the leading cause of death and healthcare costs in the United States, despite increased knowledge and management of its risk factors.(1) Cost-effective decisions regarding the prevention and treatment of CVD will only become more critical as the health and economic burdens of CVD are projected to increase over the next 20–30 years.(2, 3) CVD prevention and management policies can derive particular benefit from modeling studies due to the progressive and complex nature of the disease (a multitude of time-varying risk factors, multiple types of CVD with variable impacts on mortality and morbidity) and the multiple layers of potential intervention (screening, treatment initiation, treatment compliance, acute care, long-term care, etc.). Many studies have already quantified CVD risk using regression equations which naturally translate into probabilities for transitioning from a healthy, non-CVD health state to a composite CVD event health state.(4) These risk prediction equations play a major role in CVD prevention efforts(5), but they do not capture all relevant health and cost outcomes needed to evaluate CVD-related health interventions.

Decision-analytic models can play important roles in guiding policy on a variety of health matters. The advantage of models lies in their ability to simulate risk health and cost outcomes that would otherwise not be observable or would take several years to develop. Short-term and long-term outcomes can be calculated, and health-improving interventions can be assessed for both comparative- and cost-effectiveness. These models vary in scale and scope; simple decision problems can be sufficiently addressed using decision trees, but more complex disease areas (such as CVD) can benefit from larger policy (i.e., multi-use) models. Best practice is to fully document these models (in terms of their structure, equations, parameter values, and assumptions) and to validate these models against relevant epidemiological data to ensure the accuracy and legitimacy of their predictions.(6) Disease model validation itself is an emerging methodological field.

We have therefore developed a micro-simulation model – the Cardiovascular Disease Policy Model for Risk, Events, Detection, Interventions, Costs, and Trends (CVD PREDICT) – to project the health and cost outcomes, at both the individual and societal levels, of changes in risk factors and/or treatment status for CVD. This paper aims to satisfy two tasks: 1) describe our model in detail; and 2) perform model validation analyses using survival curves and, in a method that has not yet been used for disease model calibration or validation, receiver operating characteristic (ROC) curves (7–9).

METHODS

Our micro-simulation model, coded in C++, is the third generation of a simulation model that was originally a cohort model programmed in TreeAge (10), which was followed by a Microsoft Excel-based micro-simulation.(11) The C++ platform allows for more complexity and faster run times compared to the previous iterations of the model. Much research has been done contrasting individualistic micro-simulation models with cohort-based Markov models.(12, 13) We chose to use a micro-simulation approach to more accurately model the natural history of CVD. Specifically, the need to store and modify specific CVD risk factors on an individual basis and update individual-level CVD disease history is critical to our model, and cannot be done on a cohort level.(14) Individuals in the model do not interact with each other or other objects in the model, so it is not as complex as an agent-based model or discrete event simulation. We describe the CVD PREDICT model structure, input parameters, and key data sources here in addition to our methods for validating model performance in terms of predicting CVD and all-cause mortality using survival curves and ROC curve analysis. Full details on model calculations, parameter estimation methods, and data sources are provided in the Appendix.

Model Population

The CVD PREDICT model is populated with a database of individual patients with accompanying risk factor data. The CVD risk factors necessary to run the model are: sex, age, systolic blood pressure, total cholesterol, HDL cholesterol, currently smoking, and diabetes status. The model also considers a patient’s prior history of having a CVD event and populates these individuals in their respective CVD health states at the start of a model run. Specifically, adult participants from National Health and Nutrition Examination Surveys (NHANES) are sampled with replacement using sample weights to create a representative population of 1,000,000 individuals. The NHANES population is a representative sample for the U.S. general population, which is the target population for most CVD PREDICT model-based analyses. Risk factor distributions are therefore directly embedded in the starting model population because NHANES reports all of the variables needed at baseline to run the CVD PREDICT model.

Model Simulation

The CVD PREDICT model samples from the model population list, taking the initial set of patient risk factor characteristics for a drawn individual and simulating every subsequent year of the person’s life using Monte Carlo micro-simulation techniques and common random numbers.(15) Each individual is exposed to a series of possible events (such as death from non-CVD causes, experiencing a CVD event, having a procedure done conditional on having a CVD event, dying from a CVD event, and so no) in each model cycle. Whether or not an individual experiences an event at a given time in the model depends on a random number (i.e., luck) and the probability that that person experience that event at that time; these probabilities can depend on individual-level characteristics (which is the case for the CHD and stroke risk equations, described in more detail later) or can be fixed across individuals (such as treatment compliance), depending on the nature of these events and the granularity of the data used to estimate these inputs.

Common random numbers facilitate the comparison of interventions (such as alternative medication policies) by holding a given individual’s “luck” constant across runs; for instance, an individual that happens to die at a very young age due to non-CVD reasons will die at that age for each intervention being evaluated, so that the comparison of outcomes is more related to the signal (the effects of the intervention) and not the noise (an individual’s luck). In other words, common random numbers improve computational efficiency when running comparative analyses (such as cost-effectiveness analyses) with micro-simulation models by holding stochastic uncertainty constant across counterfactual scenarios.(15) Three main events occur in the yearly time frame: updating of the risk factors (e.g. an increase in systolic blood pressure), potential transitions into a CVD health state, and preventive interventions (e.g. screening, medication, lifestyle modifications). Costs and health state utilities are also accrued by each individual in every (yearly) model cycle. After a given individual’s remaining lifespan and CVD history are simulated with the model, a new individual is selected from the model population list and run through the model. Population totals and averages are calculated and stored once a desired number of individuals complete simulation.

Risk Factors

CVD risk factor updating can occur at each time step, in which an individual’s age is increased by one year. Updates to CVD risk factors are based on independent linear regressions based on nine waves of cross-sectional NHANES data collected between 1973 and 2010.(2) Systolic blood pressure and total cholesterol increase with age on the individual level and decrease with time based on national trends; HDL cholesterol and risk of developing diabetes increase with both age and time. Sex and smoking status (a dichotomous variable for currently smoking) remain unchanged throughout the course of a patient’s life.

Health States

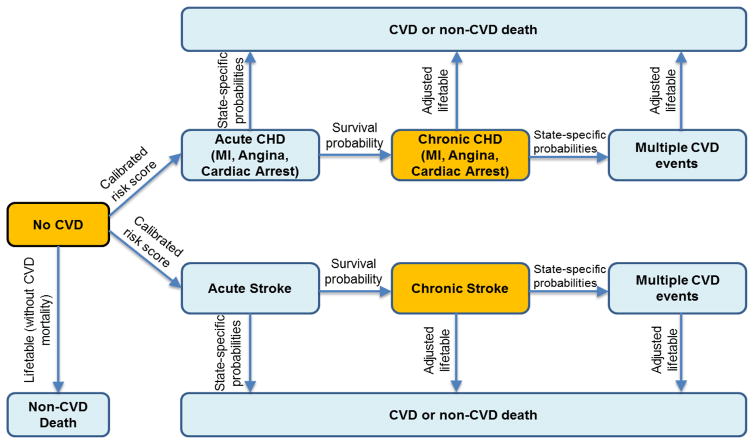
The CVD PREDICT model includes the following general health states: Disease Free (DF), Coronary Heart Disease (CHD), Stroke, and Death. The CHD health state is divided into Myocardial Infarction (MI), Angina, and Cardiac Arrest states. The MI and Angina health states are further classified as with and without revascularization, either with percutaneous coronary intervention (PCI) or coronary artery bypass graft (CABG) surgery. At any given point in time, a simulated individual can only be in one health state. We also classify disease states as acute or chronic, with the first year a patient is in a disease state considered acute, and every subsequent year a patient remains in the same disease state as chronic. A patient cannot return to the DF state after transitioning into a chronic CVD state. Figure 1 shows a simplified structure of the model of how a DF individual can transition into other health states.

Figure 1.

Simplified depiction of the cardiovascular disease state transitions used in the CVD PREDICT model. Individuals can start in any of the orange-colored health states (No CVD, Chronic CHD, Chronic Stroke). Transitions between health states are based on calibrated risks scores, case-fatality probabilities from the published literature, life table-based mortality risks, or other sources. The model simulates the CVD health and cost projections for each individual in the model until they die from CVD-related or non-CVD-related causes.

Individuals with no prior history of CVD enter into the model as DF, and those with prior history enter into the chronic state of that particular CVD event. Transitions from DF to CHD or stroke are based on separate Framingham-based risk functions. We previously calibrated these risk functions using target CHD and stroke incidence data from the Framingham Offspring Cohort (observation years 1980–2003) and Atherosclerosis Risk in Communities (ARIC, observation years 1987–2001) to calibrate the underlying CHD and stroke risk functions used in the simulation model. The results of this disease model calibration exercise are reported elsewhere.(11)

Individuals can die from a non-CVD cause while in any health state, as well as a CVD-specific cause while in a CVD state. Individuals can also have repeat CVD events while in a CVD state. Transitions in the model are hierarchical, in which an individual faces the probability of the more severe events before less severe ones. For example, a DF individual would first face the probability of a non-CVD death, then a stroke event, and finally a CHD event. Likewise, an individual in the chronic MI state would first face the probability of death (either CVD or non-CVD), then a nonfatal stroke event, and finally a repeat nonfatal MI event. If an individual has had multiple CVD events, the individual remains in the health state of the more severe event. Transition probabilities can be age- and/or sex-specific, involve multiple risk factors and disease history variables, or be based on a single probability value for all individuals. These transitions are described in more detail in the Appendix.

Transition Probabilities

Table 1 lists key one-year transition probabilities and their sources for the CVD PREDICT model applied to a U.S. setting. We classify transition probabilities as coming from a health state, such as “from DF” or “from MI”. We briefly describe five main types of transitions here: CVD events, non-CVD mortality, acute CVD mortality, chronic CVD mortality, and repeat CVD events. CHD events are further divided into cardiac arrest, MI, and angina health states, each with its own case fatality, quality-of-life, and cost consequences. The proportion of both cardiac arrest and MI were taken from U.S. data, with the remaining proportion assigned to angina.(16, 17) More details on these calculations can be found in the appendix. Non-CVD mortality was calculated by removing CVD mortality from all-cause life tables. We used sex-specific all-cause mortality life tables from the Centers for Disease Control and Prevention (CDC); age- and sex-specific CVD-specific death rates (also published by the CDC) were subtracted from the life table annual rates to estimate non-CVD mortality rates, which were converted back to annual probabilities.

Table 1.

Disease progression inputs used in the CVD PREDICT model

Parameter	Value	Source
From Disease Free State
Non-CVD death	Age and sex-specific table	NCHS 2010 (42)
Stroke event	Calibrated risk score	Wolf 1991 (43)
CHD event	Calibrated risk score	Anderson 1991 (44)
% CHD Cardiac Arrest	Age and sex-specific table	Weinstein 1987 (45)
% CHD MI (male)	0.35	NHLBI 2006 (17)
% CHD MI (female)	0.2	NHLBI 2006 (17)
From Stroke state
Acute (1-year) risk of death	0.15	Carandang 2006 (46)
Chronic (post 1st-year) MI	0.022	Touze 2005 (47)
Chronic (post 1st-year) stroke	Calibrated risk score	Wolf 1991(43)
From MI state
Acute (1-year) risk of death	0.15	Mozaffarian 2016 (1)
Acute CABG	0.082	Fang 2010 (48)
Acute PTCA	0.3	Fang 2010 (48)
% Procedure death	0.0015	Williams 2006 (49)
Acute 2nd MI (no PTCA)	0.06	Capewell 2006 (50)
Acute 2nd MI (after PTCA)	0.053	Windecker 2014 (51)
Chronic (post 1st-year) repeat MI	0.064	Jokhadar 2004 (52)
Chronic (post 1st-year) repeat MI (with PTCA)	0.052	Jokhadar 2004 (52), Windecker 2014 (51)
From MI and CABG State
Acute post-CABG death	0.027	Peterson 2004 (53)
Acute 2nd MI	0.047	Windecker 2014 (51)
Repeat MI	0.049	Yusuf 1994 (54), Windecker 2014 (51)
From Angina State
Acute (1-year) risk of death	0.045	Capewell 2006 (50)
Acute (1-year) risk of cardiac arrest	0.006	Hsia 2008 (55)
Acute (1-year) risk of MI	0.035	Hemingway 2003 (56)
Acute (1-year) risk of MI (with PTCA)	0.031	Hemingway 2003 (56), Windecker 2014 (51)
Acute CABG	0.2	Ford 2007 (57)
Acute PTCA	0.3	Ford 2007 (57)
% Procedure Death	0.0015	Assumption: same as MI
Chronic (post 1st-year) MI	0.035	Assumption: same as acute MI
Chronic (post 1st-year) MI (with PTCA)	0.029	Windecker 2014 (51)
From Angina and CABG state
Acute post-CABG death	0.027	Assumption: same as MI-CABG
Acute 2nd MI	0.028	Windecker 2014 (51)
Chronic (post 1st-year) MI	0.0278	Hemingway 2003 (56); Windecker 2014 (51)
From Cardiac Arrest state
Acute (within 1 year) death	0.954	Nichol 2008 (58)
MI event	0.064	Assumption: same as MI
Chronic (post 1st-year ) CVD Mortality
Proportion of chronic CVD deaths due to CVD	0.28	NHANES-based calculation
Post-stroke all-cause mortality multiplier	2.3	Rosen 2010 (59)
Post-CHD all-cause mortality multiplier (male)	1.6	Smolina 2012 (60)
Post-CHD all-cause mortality multiplier (female)	2.1	Smolina 2012 (60)
Post-CHD all-cause mortality >1 event (male)	3.4	Smolina 2012 (60)
Post-CHD all-cause mortality >1 event (female)	2.5	Smolina 2012 (60)

Acute (within one year of an event) and chronic (all years after the first year of an event) all-cause mortality were modeled separately for each event state. Acute mortality rates from stroke, cardiac arrest, and angina events are taken directly from various observational studies with U.S. sources, or when U.S. data were lacking, from other developed countries. We also accounted for acute CVD mortality for individuals who experience multiple CVD events within a given year (e.g. cardiac arrest following angina in the same year) using point estimates representing the U.S. in published literature. We applied CVD event-specific multipliers to all-cause life tables to estimate chronic CVD mortality; these multipliers were sex-specific and were higher for individuals with history of >1 CVD event. Risks of secondary CVD events were drawn from studies in the U.S. or other developed countries. Table 1 lists these values; the appendix contains more details on these calculations.

Model Outputs

The CVD PREDICT model keeps track of every CVD event for every individual run through the model, including the number of deaths arising from each type of CVD event, average life expectancy of those with and without CVD, the number of individuals who have ever had a CVD event, and yearly prevalence of every disease state. For cost-effectiveness analyses, the model outputs average lifetime per-person discounted costs and quality-adjusted life years (QALYs). The appendix contains more details on the inputs specific to cost-effectiveness analyses, including probabilistic sensitivity analysis, utility values (Appendix Table A-1), cost inputs (Appendix Table A-2).

Screening and Medical Treatment Interventions

The CVD PREDICT model incorporates CVD screening based on individual risk factors and/or calculated CVD risk scores. Screening in the model can lead to medical treatment for primary CVD prevention in the general population. Disease-free individuals become eligible for statin and aspirin therapy if they are deemed at high risk for CVD (exceeding a pre-determined threshold, such as >7.5% 10-year ASCVD risk, LDL cholesterol >190 mg/dL, or having type I or II diabetes). Moreover, we model treatment eligibility for anti-hypertensive medications if an individual’s systolic blood pressure exceeds a certain level (such as >140 mmHg). Each of these three types of drugs has its own compliance and initiation rate, and each drug that an individual is on leads to a relative risk reduction of both CHD and stroke. A combination of drugs produces a combined multiplicative effect. The model includes risks and consequences of adverse events associated with taking a statin. The Appendix shows how we modeled older CVD screening guidelines in our validation analyses to better reflect secular trends in treatment eligibility.

The model additionally accounts for secondary prevention medications, which can reduce probabilities of death or another CVD event once an individual is already in a CVD state. We model four distinct secondary preventions: statins, aspirin, ACE inhibitors, and beta blockers. Like primary prevention methods, each secondary prevention method involves compliance and initiation, and initiation rates differ for those in CHD and stroke states. The appendix contains additional details on medical intervention used in the CVD PREDICT model (Appendix Table A-3) with particular attention on treatment effectiveness inputs (Appendix Table A-4).

Model Validation Analyses

We validated our calibrated simulation model by comparing CVD PREDICT model-predicted all-cause and CVD mortality against observed and predicted mortality data from the NHANES 1999–2000 population ages 35–80 years at baseline (baseline data collected 1999–2000; cause-specific mortality data available through 2011). We used sample weights and restricted our primary analyses to individuals with complete baseline data in the NHANES population. We performed validation analyses with imputed missing baseline values in a sensitivity analysis. The nationally representative model population of one million individuals was created by weighted sampling with replacement from the NHANES 1999–2000 cohort.

The NHANES follow-up mortality data only include categories of death (as opposed to more specific causes of death). Table 2 shows how we defined CVD death for the observed NHANES data and in simulation model. Model-predicted CVD mortality was defined by summing acute post-event mortality (i.e., any death within the first year of the event) and a percentage (28.2%) of post-event deaths (i.e., any time after the event) due to the separate estimation of acute and post-1st year mortality in cardiovascular disease health states in the model. We calculated the percentage of post-event deaths as CVD based on follow-up data from the NHANES cohort. Specifically, we calculated the percentage of all observed deaths due to CVD out of all deaths observed in the follow-up period (1999–2011) for individuals starting with history of CVD (7.2% of the cohort). We performed this calculation because of how mortality was estimated in chronic CVD states. Specifically, we applied multipliers to all-cause life tables for individuals in CHD and stroke health states, which do not allow for parsing of non-CVD-related and CVD-related mortality for individuals that died in these chronic states.

Table 2.

Comparison of CVD Mortality Causes

NHANES 1999–2000 (ICD codes)	CVD PREDICT model
Disease of the heart (I00-I09, I11, I13, I20-I51)	Acute MI (within one year of the event)
Cerebrovascular disease (I60-I69)	Acute angina & cardiac arrest A proportion (28%) of chronic CHD death (deaths after 1st year post-MI, angina, or cardiac arrest) Acute & a proportion (28%) of chronic stroke death CABG procedure death PTCA procedure death

Note: “MI” stands for myocardial infarction, “CABG” stands for coronary artery bypass grafting procedure, “PTCA” stands for percutaneous transluminal coronary angioplasty procedure

We used the common starting population from NHANES 1999–2000 to generate survival curves for three types of follow-up: 1) observed deaths in the NHANES follow-up data; 2) modeled deaths in the simulation model; and 3) projected deaths only using all-cause U.S. life tables from the CDC (i.e., not modeling CVD events or splitting out causes of death). We did not evaluate CVD death for the third method because the life tables include all causes of mortality. We were able to compare additional projections of 20- and 30-year all-cause mortality and life expectancy for the simulation model and life table projections, but not for the observed NHANES outcomes due to follow-up stopping in 2011. Individuals in the baseline NHANES 1999–2000 population were drawn with (weighted) replacement to create 1,000 bootstrap samples used to derive 95% confidence intervals for benchmark points (e.g., 5-year and 10-year survival) on the observed survival curves. The Hosmer-Lemeshow goodness-of-fit test (chi-square statistic, where lower p-values suggest worse fit) was used to compare observed to predicted mortality outcomes (10- and 5-year all-cause and CVD mortality).

In addition to generating survival curves, we assessed model validation by comparing CVD PREDICT model-based mortality risk on an individual level to observed outcomes using receiver operating characteristic (ROC) curve analysis. To do this, first we ran each individual in the baseline population through the CVD PREDICT model 1,000 times over a 10-year time horizon without using common random numbers. For a given individual, their survival varies over the course of these 1,000 model runs due to chance; survival varies across persons in the model due to their individual characteristics (such as age, sex, blood pressure, cholesterol, etc.). We calculated the percentages of iterations that a given individual survived 5 or 10 years from all-cause and CVD mortality to estimate their CVD PREDICT model-based 5-year and 10-year mortality risks. After doing this for each individual in the population, we ranked them by their CVD PREDICT model-based mortality risk. These ranks were compared to observed mortality outcomes on an individual basis to generate ROC curves, with individual-level observed 5- and 10-year mortality statuses used as reference standards. The ROC curve plots sensitivity (the true positive ratio) against one minus specificity (the false positive ratio). For our analyses, a true positive would be an individual predicted to die within a given time frame (5 or 10 years) based on their CVD PREDICT mortality risk ranking who actually died in the same time frame in the observed NHANES follow-up data.

The CVD PREDICT model was programmed in Microsoft Visual C++ 2005 and all validation analyses were performed using SAS Version 9.4.

Study Funding

This study was funded by grant No. 5R01HL104284-03 to the Harvard T.H. Chan School of Public Health from the National Heart, Lung, and Blood Institute. The funding source had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; or the decision to submit the manuscript for publication.

RESULTS

Baseline Population Characteristics

Weighted baseline characteristics for the NHANES 1999–2000 population limited to those with complete baseline data and the corresponding averages for the same population with imputed values are reported in Table 3. Most (83.2%) of individuals in the NHANES ages 35–80 had complete data needed for the risk functions used by the CVD PREDICT model. Cholesterol values (14.5% missing) and systolic blood pressure values (11.0% missing) were the most common missing variables in the analytic sample with substantial overlap (8.7% of analytic sample missing both variables). Mortality status, cause of death, and follow-up time information was complete for all individuals except for nine individuals (0.2% of the analytic sample) who were assumed to be alive at last point of contact but had follow-up times between 5 and 10 years (i.e., these individuals had complete follow-up data for a 5-year analysis but not for a 10-year analysis).

Table 3.

NHANES Population Characteristics (starting ages 35–80 years)

Characteristics or outcomes	Weighted NHANES 1999–2000 without imputation(n=2,689)	Weighted NHANES 1999–2000 with imputation(n=3,232)
Male	47.9%	47.6%
Age (years)	51.9 (13.0)	52.1 (13.19)
Systolic blood pressure (mmHg)	126.1 (21.4)	126.4 (20.6)
Total Cholesterol (mg/dL)	210.1 (39.7)	210.0 (36.7)
HDL Cholesterol (mg/dL)	51.3 (15.8)	51.2 (14.8)
Current smokers	19.6%	19.6%
Self-reported diabetes	9.9%	10.3%
History of myocardial infarction	4.6%	4.4%
History of stroke	2.6%	2.8%
All-cause death within 10 years	11.2%	12.0%
CVD death within 10 years	2.2%	2.4%

Note: values are either percentages or means; standard deviations shown for continuous variables shown in parentheses

Model Validation

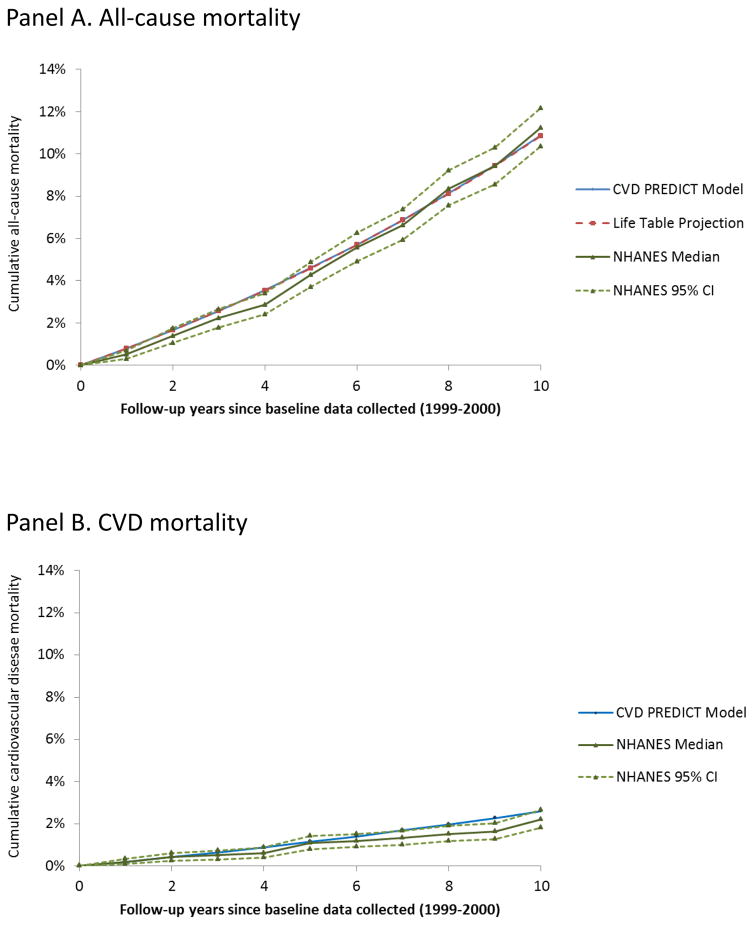
Figure 2 shows survival curves for all-cause mortality (Figure 2 Panel A) and CVD mortality (Figure 2 Panel B) based on observed NHANES follow-up data (median and 95% confidence limits from the bootstrap analyses), the CVD PREDICT model projections, and life table projections for the same starting population. Five-year and 10-year CVD and all-cause mortality from the CVD PREDICT model fell within the 95% confidence intervals of the observed data. Observed 10-year all-cause mortality in NHANES versus the CVD PREDICT model were 11.2% (95% CI: 10.3–12.2%) versus 10.9%; corresponding results for CVD mortality were 2.2% (1.8–2.7%) versus 2.6%. Observed 5-year all-cause mortality in NHANES versus the CVD PREDICT model were 4.3% (95% CI: 3.7–4.9%) versus 4.6%; corresponding results for CVD mortality were 1.1% (0.8–1.4%) versus 1.2%. Survival curves based on a starting population that included imputed values are shown in Appendix figure A-1 and showed similar comparisons, with slightly higher all-cause mortality in the observed NHANES data (10-year all-cause mortality 12.0% [11.0–13.0%]).

Figure 2.

Survival curves for individuals in the 1999–2000 NHANES population ages 35–80 years. The proportion of individuals surviving from all-cause (Panel A) or CVD-related (Panel B) mortality over 10 years of follow-up data observed in the NHANES population (solid green lines represent median values from 1000 bootstrap simulations, dotted green lines show 95% confidence intervals) compared to the CVD PREDICT model (blue line) and life table projects (red line, Panel A only).

CVD PREDICT model-based all-cause mortality projections at 20 and 30 years were 27.7% and 47.8%; corresponding results for the life table extrapolation of the same starting population were 28.1% and 48.9%, respectively. Life expectancy was 82.5 and 81.7 years for the CVD PREDICT model-based and life table-based projections, respectively.

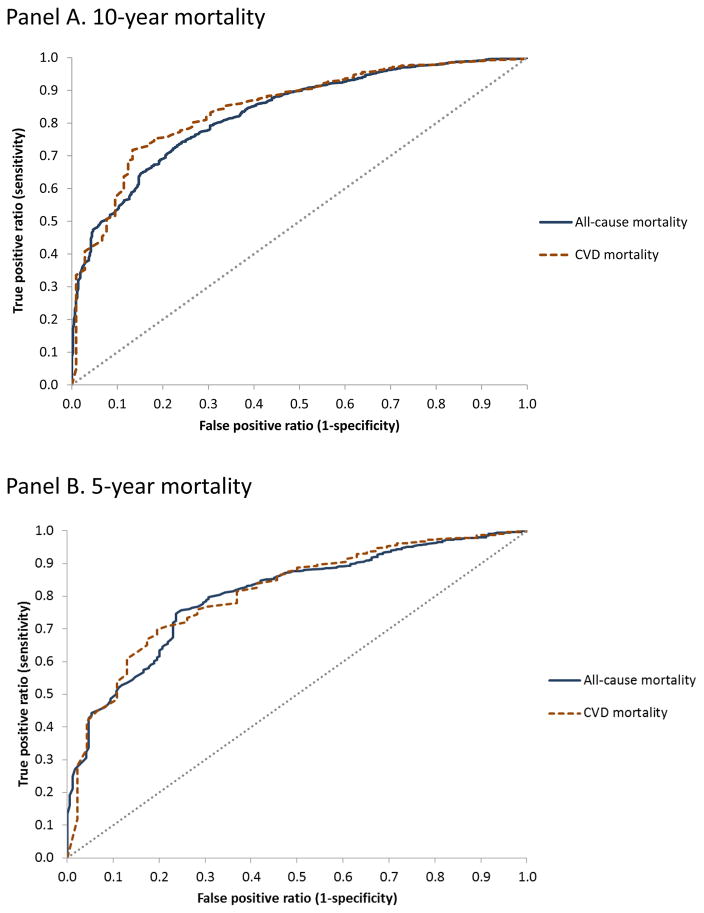
Figure 3 shows ROC curves for CVD PREDICT model-predicted 10-year (Figure 3 Panel A) and 5-year (Figure 3 Panel B) mortality risks (both all-cause and CVD mortality shown) compared to observed NHANES outcomes (the reference standard). Areas under the ROC curves (AUCs) for model-predicted 10-year all-cause and CVD mortality risks were 0.83 (0.81–0.85) and 0.84 (0.81–0.88), respectively; corresponding results for 5-year risks were 0.80 (0.77–0.83) and 0.81 (0.75–0.87), respectively. ROC curves based on a starting population that included imputed values are shown in Appendix figure A-2 and showed similar findings (all AUC values were >0.80).

Figure 3.

Receiver operating characteristics (ROC) curves for CVD PREDICT model-predicted mortality risk.

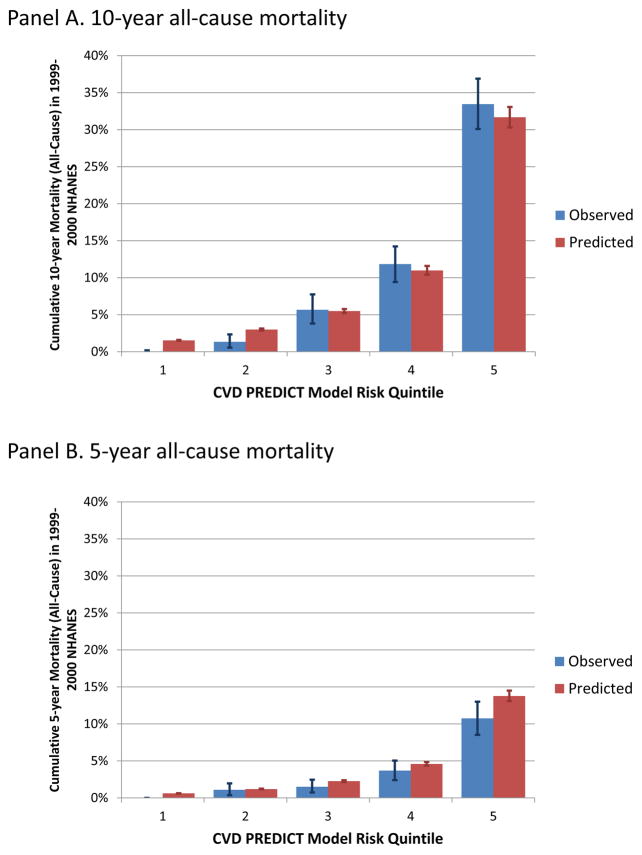
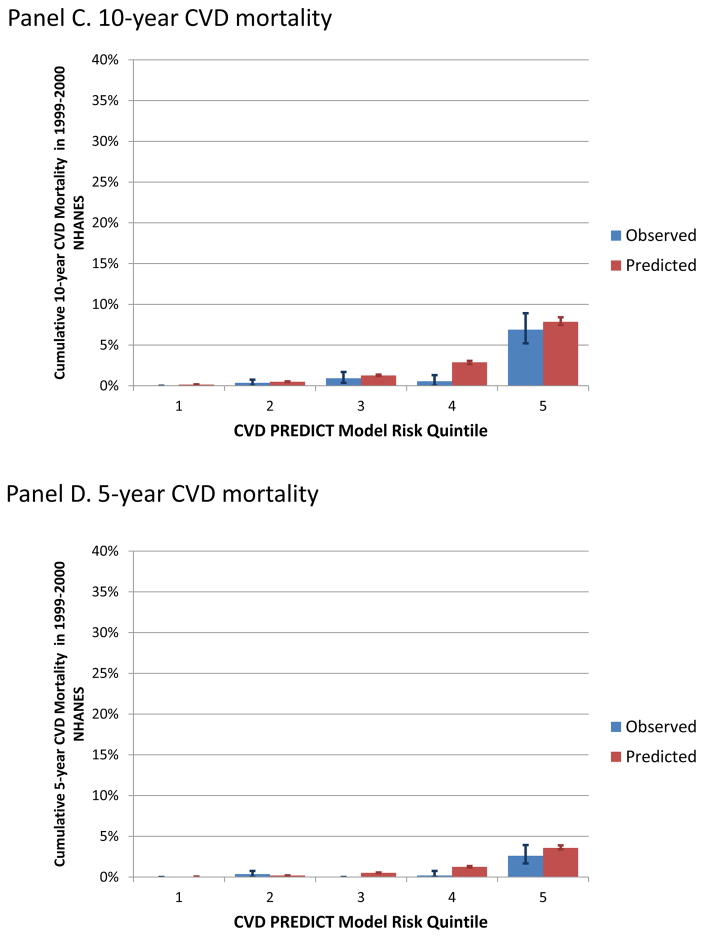
Appendix figure A-3 (Panels A-D) shows observed versus predicted mortality outcomes (10- and 5-year all-cause and CVD mortality) by CVD PREDICT model-based quintiles. Predicted mortality outcomes were within 95% confidence intervals of observed mortality outcomes with the exception of the 4^th highest risk quintile for CVD mortality, where the CVD PREDICT model predicted more deaths than were observed in the NHANES data, and the two lowest risk quintiles for all-cause mortality, where the CVD PREDICT model predicted fewer deaths than were observed in the NHANES data (all Hosmer-Lemeshow p-values <0.10).

DISCUSSION

We developed a CVD micro-simulation model coded in C++ (the CVD PREDICT model) that integrates individual-level risk factors, epidemiologic inputs, separate CHD and stroke risk equations, case fatality risks, screening and treatment interventions, and utility and cost data into a single model. As opposed to a regression-based risk prediction model that is intended to be used in clinical practice, the CVD PREDICT model is a decision analytic model intended to evaluate the comparative- and cost-effectiveness of CVD policies. The model was validated to observed U.S. CVD mortality data from NHANES fitting within a reasonable range of values.

External validation is an important criterion for assessing the quality and usefulness of disease models, but few CHD policy model have been calibrated or validated.(6, 18, 19) Although there are no common quantitative standards for assessing goodness of fit(6, 20), the ability of the CVD PREDICT model to match observed outcomes is similar to other recent CVD policy model validation studies.(21–23) A review of 154 calibrated cancer simulation models showed that 52% of them mentioned model validation(24); CVD risk functions are rarely validated externally.(25)

We leveraged the individual-level longitudinal NHANES data in our validation analyses in two ways by generating survival curves as well as ROC curves. The CVD PREDICT model demonstrated excellent external validity by both measures. Mortality outcomes from the CVD PREDICT model mostly fell within 95% confidence intervals based on observed NHANES data (with the exception of CVD mortality near or just over the upper confidence interval years 7–10 for CVD mortality), and the AUCs were consistently >0.80. A review of regression-based CVD risk prediction scores found that only 5 out of 17 external validations had AUCs greater than 0.77.(26)

The ROC curve approach has not previously been used for validation of disease simulation models (referring here to models such as decision analytic models, Markov models, micro-simulations, and so on, as opposed to regression-based risk prediction models), but both methods add important information on model performance. For instance, limiting validation analyses to survival curves could be misleading if the simulation model had the wrong (i.e., lowest-risk) individuals dying over 5 or 10 years but resulted in similar average population-level 5- or 10-year mortality outcomes observed in the validation dataset. This type of individual-level mismatch of outcome predictions could lead to errors when modeling the effects of targeted interventions. Conversely, ROC curves are constructed using rank values, so high AUC values could be produced for a simulation model that does not predict absolute mortality risk well. The idea of the joint importance of risk calibration (expected outcomes matching observed outcomes) and risk discrimination (area under the ROC curve) has been discussed for regression-based risk prediction models, but our analysis shows this can be done for simulation models as well if individual-level follow-up validation data are available.(27, 28) Presenting the ROC curves themselves can inform modelers and/or decision-makers on how the simulation model performs in the “high sensitivity/low specificity” and “low sensitivity/high sensitivity” regions of the curve, which could be useful if the model is used to evaluate targeted interventions (i.e., interventions target high- or low-risk individuals.)

The CVD Policy Model (formerly the CHD Policy Model) has been used to evaluate the cost-effectiveness of several CVD projection and prevention studies over several decades; this model has been well-validated in previous studies with a focus on replicating treatment effects from anti-hypertensive and statin medication trials.(16, 29–31) Our CVD PREDICT model differs from the CVD Policy Model in two important respects. First, in contrast to the deterministic Markov modeling approach used in the CVD Policy Model, our CVD PREDICT model is a micro-simulation (which simulates heterogeneous individuals one at a time, as opposed to Markov models which rely on simulating and aggregating the results from multiple “cells” of individual profiles). Second, our validation analysis used nationally representative NHANES data and mortality outcomes as opposed to validating to treatment effects from clinical trials. Despite these methodological differences both models have been found to arrive at similar policy recommendations in related decision-analytic studies, such as expanded treatment eligibility for low-cost statins used in primary CVD prevention in the U.S., which is some evidence of cross-validation performance for both models.(6, 32, 33)

Model-based economic evaluations of CVD-related health policies are increasingly common and policy-relevant in the U.S.(34, 35) Specifically, in 2014 the American College of Cardiology/American Heart Association acknowledged that cost-effectiveness should be the basis for determining value in cardiovascular disease health policies, but noted that the primary barrier to shifting towards valued-based case “is the lack of high-quality data on cost and value (cost-effectiveness) of interventions or procedures used in practice.”(35) Our simulation is designed to be flexible enough to evaluate a wide range of CVD-related policies as opposed to being a “single-use” model, which is why we invested in a rigorous external validation against nationally representative, longitudinal data.(36) Selected examples of previous and potential applications of our model include staged screening for CVD risk, identifying high-risk primary aldosteronism patients eligible for intensive CVD prevention procedures, and population-based policies focusing on important health behaviors such as diet and exercise.(11, 37, 38)

A limitation of our model, as with all other decision-analytic models, is the abundance of data required as input, as well as the uncertainties underlying the data. As documented, we relied on various assumptions for which certain data that do not exist. It was also necessary at times to mix epidemiological inputs from non-U.S. settings in our U.S.-based model. There are some aspects of clinical care, such as use of angiotensin II receptor blockers for blood pressure control, that we do not explicitly model to balance additional model detail against limiting model complexity. Similarly, we did not include several CVD risk factors in our underlying risk functions, such as c-reactive protein and coronary artery calcification, that might improve prediction but increase the data requirements of the model; certainly, these predictors could be evaluated by the model in similar fashion to studies by Lee et al. and Pletcher et al. We also did not explicitly model interactions between individuals, which previous studies have shown to influence CVD risk factors(39, 40). Our model therefore cannot exactly be expected to perfectly replicate or forecast actual outcomes. We were also limited by not being able to validate to our model any other outcome aside from mortality due to NHANES follow-up data limitations.

Along these lines, due to lack of other data sources we had to estimate the proportion of all-cause mortality due to CVD (28%) for those in chronic CVD states by calculating the percent of all deaths due to CVD among individuals in the NHANES population with history of CVD at baseline. This value (28%) might seem low given national data that show CVD accounts for 31% of all deaths (and one could assume the proportion of deaths due to CVD would be higher among those with a history of CVD), but the proportion of deaths attributable to CVD in the NHANES validation population for those without history of CVD at baseline was 17%, which suggests CVD might have been underreported as a cause of death in the NHANES data.(1) In any case, this value (28%) does not affect any transitions in the model, but instead was used to assign a proportion of all-cause mortality experienced in chronic CVD health states to CVD (i.e., it was used for mortality accounting purposes as opposed to driving underlying risk in the model, so it would not affect our all-cause mortality results). There may also be some minor variations between the ICD-10 classification of CVD deaths in the NHANES data and the CVD PREDICT model that could contribute to some differences in CVD mortality particularly in later years (7–10 years from baseline). Although the Hosmer-Lemeshow statistics were significant, we believe these results are not clinically relevant due to the fact that almost all of the CVD deaths observed in the NHANES population occurred in the highest risk quintile.

Finally, many CVD risk factors and treatments in the U.S. have evolved over the past 30 years, so although our model might have external validity in the present tense, it might have less predictive ability in future years. The CVD PREDICT model directly updates some risk factors (such as blood pressure and cholesterol) with age and time, but other model inputs (such as case fatality risks) are fixed over time. New treatments could be developed or existing treatment use could change over time, which could also alter projections of CVD burden to the extent that these changes in treatment rates are not captured in the year coefficients for the regressions that update blood pressure and cholesterol values each year in the model. We also do not explicitly model quitter behavior for current smokers. Performing extensive sensitivity and uncertainty analyses is important for these and all model inputs, which is true for all decision-analytic models.(41)

We have described the CVD PREDICT model structure, calculations, and data sources in detail and subjected its projections to rigorous tests of external validation that are not commonly performed for similar models. The CVD PREDICT model demonstrated that it can predict actual disease outcomes of policy relevance (all-cause and CVD mortality), which should provide some reassurances to decision-makers who choose to use the projections and recommendations based on applications of the model.

Appendix: Detailed specifications of transition probabilities, utility and cost inputs, and treatment inputs for the CVD PREDICT model

Transition Probabilities

In this section, we give details for the CVD PREDICT model inputs that were calculated and adjusted. Other parameters are listed in the main text (Table 1) with their respective sources.

Proportion of CHD events

a. Cardiac Arrest

The proportion of cardiac arrest among CHD events is calculated using data from the Weinstein, et al, study.(1) The proportion is estimated using the probabilities by age and sex that an initial CHD event would be a cardiac arrest.

If age < 40:

$$P(\mathit{cardiac}\mathit{arrest})=\frac{P(\mathit{initial}\mathit{CHD}\mathit{event}is\mathit{cardiac}\mathit{arrest},\mathit{age}40)}{40}\times \mathit{current}\mathit{age}$$

For ages between 40 and 49:

$$\begin{array}{l}P(\mathit{cardiac}\mathit{arrest})\\ =P(\mathit{initial}\mathit{CHD}\mathit{event}is\mathit{cardiac}\mathit{arrest},\mathit{age}40)\\ +\frac{P(\mathit{initial}\mathit{CHD}\mathit{event}is\mathit{cardiac}\mathit{arrest},\mathit{age}50)-P(\mathit{initial}\mathit{CHD}\mathit{event}is\mathit{cardiac}\mathit{arrest},\mathit{age}40)}{10}\\ \times (\mathit{current}\mathit{age}-40)\end{array}$$

Age groups between 50 and 59, 60 and 69, 70 and 79 are calculated in the same manner as that of ages between 40 and 49.

For ages over 80:

$$P(\mathit{cardiac}\mathit{arrest})=P(\mathit{initial}\mathit{CHD}\mathit{event}is\mathit{caridiac}\mathit{arrest},\mathit{age}80)$$

b. Myocardial Infarction

The proportion of MI patients is estimated using the NHLBI chart book.(2) We assume that the total incidence of CHD would be equal to the sum of the incidence of MI and angina. Therefore, the proportion of MI is calculated as below:

$$P(MI)=\frac{\mathit{Incidence}ofMI}{\mathit{Incidence}ofMI+\mathit{Incidence}of\mathit{angina}}$$

c. Angina

The proportion of Angina is calculated by subtracting the proportion of MI and proportion of cardiac arrest from 1.

$$P(\mathit{angina}\mathit{among}\mathit{CHD}\mathit{events})=1-P(MI)-P(\mathit{cardiac}\mathit{arrest})$$

From Myocardial Infarction (MI) Transitions

a. Acute (1^st-year) MI death

The probability of death (from any cause) within one year of experiencing an MI (15%) is based on a computation from the 2016 Update of Heart Disease and Stroke Statistics from the American Heart Association.(3)

b. Second (1^st-year) MI

The transition probability of experiencing a second MI after an acute MI (AMI) is from a Scotland-based cohort study on the outcomes of patients admitted with angina or MI.(4) The study estimates the probability of a fatal or non-fatal event in men after a first admission for acute coronary syndrome. We measure the difference between cumulative proportions of ‘Death’ and ‘Death+AMI’ at 12 months to find the cumulative proportion of getting a second MI after a first admission for AMI. The same method is used for females, and then we calculate the un-weighted average between males and females for our model.

c. Second MI Post-PTCA

The risk of second (1^st-year) MI following MI with a PTCA procedure was based on a network meta-analysis that included 262,090 patient years of follow-up (5); the relative risk of MI in patients with stable CHD was 0.88 for all trials (regardless of study follow-up length). We applied this relative risk to the risk of second (1^st-year) MI above.

d. Chronic (post 1^st-year) MI (i.e., repeat MI)

An Olmsted County, Minnesota study on the incidence of sudden cardiac death and recurrent ischemic events after MI is used to get the probability of a repeat MI.(6) This study shows that the 3-year event-free survival rate of repeat MI is 82%. We use this survival rate to get the 3-year cumulative incidence of repeat MI:

$$3yr\mathit{cumulative}\mathit{incidence}of\mathit{repeat}MI=1-\frac{\mathit{survival}\mathit{without}2ndMI}{\mathit{population}\mathit{with}1stMI}$$

Cumulative incidence is then converted to an annual rate and then an annual probability for the model. For patients with PTCA, this risk was multiplied by a relative risk of 0.82, which was an estimate from Windecker et al 2014 meta-analysis limited to trials with ≥ 24 months follow-up.

e. Chronic (post 1^st-year) stroke

Long-term risk of stroke for patients in chronic CVD states is based on the same calibrated risk function used to predict stroke from the Disease Free state; however this risk function does include history of CVD as a predictor.(7)

From MI with Coronary Artery Bypass Graft (CABG) Procedure Transitions

a. Second Acute (1^st-year) MI

The relative risk for CABG of MI in patients with stable CHD was 0.79 for all trials (regardless of study follow-up length) in the Windecker et al 2014 meta-analysis. We applied this relative risk to the risk of second (1^st-year) MI above.

b. Chronic (post 1^st-year) MI (i.e., repeat MI)

The relative risk for CABG of MI in patients with stable CHD was 0.77 for trials with ≥ 24 months follow-up. We applied this relative risk to the risk of chronic (i.e., repeat) MI above.

c. Chronic (post 1^st-year) stroke

Long-term risk of stroke for patients in chronic CVD states is based on the same calibrated risk function used to predict stroke from the Disease Free state; however this risk function does include history of CVD as a predictor.(7)

From Angina Transitions

a. Acute (1-year) angina death

The probability of death after an acute angina event is from a Scotland-based cohort study on the outcomes of patients admitted with angina or MI.(4) The study estimates the probability of events after the first admission for acute coronary syndrome, and we take the value for death at 12 months. For the model, we calculate the un-weighted average between males and females.

b. Acute (1-year) arrest

The probability of having an arrest after an acute angina event is taken from a study which analyzed the Prevention of Events with Angiotensin Converting Enzyme Inhibition (PEACE) trial to predict sudden cardiac death (SCD) in patients with stable coronary artery disease and preserved left ventricular systolic function.(8) From their cumulative incidence of SCD by risk score, we estimate the cumulative incidence of SCD in the median risk score group to be 0.006.

c. Acute (1-year) MI

The probability of having an MI after an acute angina event is calculated using a study that examined the outcome of angina comparing patients with and without the diagnosis of doctors, and also comparing patients with and without abnormal cardiovascular test results.(9) The study reported 5-year cumulative incidence based on reports of angina with diagnosis by doctor (both abnormal test and no abnormal test) and reports of the most serious event over 5-year follow up is MI. We take the raw average of these two values, 0.16 and 0.17, and considered it the 5-year cumulative incidence of MI after angina. Cumulative incidence is then converted to an annual rate and then an annual probability for the model. For patients with PTCA, this risk was multiplied by a relative risk of 0.88, which was an estimate from Windecker et al 2014 meta-analysis for all trials.

d. Chronic (post 1^st-year) stroke

Long-term risk of stroke for patients in chronic CVD states is based on the same calibrated risk function used to predict stroke from the Disease Free state; however this risk function does include history of CVD as a predictor.(7)

From Angina with Coronary Artery Bypass Graft (CABG) Procedure Transitions

a. Chronic (post 1^st-year) MI

The relative risk for CABG of MI in patients with stable CHD was 0.77 for trials with ≥ 24 months follow-up. We applied this relative risk to the risk of chronic (i.e., repeat) MI above.

b. Chronic (post 1^st-year) stroke

Long-term risk of stroke for patients in chronic CVD states is based on the same calibrated risk function used to predict stroke from the Disease Free state; however this risk function does include history of CVD as a predictor.(7)

From Cardiac Arrest Transitions

a. Acute (1-year) cardiac arrest death

The probability of acute death within one year is from a study that examined the incidence and outcome of cardiac arrest across different regions.(10) The percentage of cardiac arrest patients that were discharged alive is subtracted from 1 to get the probability of acute death among cardiac arrest patients.

b. Chronic (post 1^st-year) stroke

Long-term risk of stroke for patients in chronic CVD states is based on the same calibrated risk function used to predict stroke from the Disease Free state; however this risk function does include history of CVD as a predictor.(7)

From Stroke Transitions

a. Acute (1-year) stroke death

Framingham data from 1990–2004 and a review of other stroke-specific studies report a range of 30-day stroke mortality of 15–30%.(11) Since stroke case fatality has declined in recent years, we use the lower bound (15%) to estimate one year mortality risk from stroke.(12)

b. Chronic (post 1^st-year) stroke (i.e,. repeat stroke)

Long-term risk for repeat stroke is based on the same calibrated risk function used to predict stroke from the Disease Free state; however this risk function does include history of CVD as a predictor.(7)

c. Chronic (post 1^st-year)

Long-term annual risk of MI after stroke (2.2%) is based on a systematic review and meta-analysis of cohort studies that included stroke patients with a mean follow-up time of 3.5 years.(13)

Utility and Cost Inputs

Utilities

The majority of our utility data come from the Sullivan et al. study on the preference-based EQ-5D index scores for chronic conditions in the U.S.(14) This study presented median EQ-5D values of chronic and acute stroke, MI, and angina (14), but not cardiac arrest, so we used a European cost-effectiveness analysis to estimate cardiac arrest utility.(15) The utility of MI-CABG and angina-CABG are assumed to have an equal utility with MI and angina, respectively. Due to lack of utility data specifically for acute disease states (i.e., within one year of the event) we assumed an additional (acute) disutility for the first year of experiencing the CVD event quantified by the regression coefficient for condition-specific disutility from Sullivan et al (15); for acute cardiac arrest, we assumed the same additional disutility as MI (-0.0409). For CVD events that can occur repeatedly (MI, stroke), we apply a disutility in the year of each occurrence and returned a patient’s utility to its baseline the following year.

For the Disease Free state, we use a range of utility values, ranging from the median general population value from Sullivan et al (0.844) to perfect health (1.0), knowing the true range is somewhere in between because the median general population value includes individuals with CVD. For a point estimate to use in base-case analyses, we regarded the overall population median utility value from Sullivan 2005 (0.844) as a weighted average of the utility for persons with CVD (median value about 0.778 from Sullivan et al) and without CVD, using the prevalence of CVD (33%, per the 2016 update of the American Heart Association CVD statistics report) in the weighting. This calculation leads to [0.844 0.333*(0.778)] / 0.667 = 0.877 for the average utility without CVD.

The disutility occurred from adverse events by statin usage was calculated using data from a cost-effectiveness study on C-reactive protein testing.(16) The study considered minor statin adverse events as two days of life lost, and the major statin adverse event as two weeks of life lost, which we converted to a utility index score. Table A-1 contains all of the utility values used in the model.

Costs

Costs represented in the model include the cost of chronic and acute disease states, surgical procedures, screening, treatment, and side effects from statin. Table A-2 lists the cost inputs with their respective sources.

The disease-free state is assumed to incur no CVD-related costs. The costs of acute disease states (stroke, MI, cardiac arrest, and angina) are taken from a study on health care costs and utilization using claims data from a large U.S. health plan (over 14 million geographically diverse participants). When costs are categorized by non-fatal and fatal states, we calculate the weighted average to determine total annual cost using the case-fatality of each condition as the weight. Chronic health state costs are taken directly from various sources that conducted cost studies for each individual health state. For example, the cost of chronic stroke is estimated from a study looking at the cost of ongoing care for stroke.(17)

Costs of surgical procedures, screening, medication, and statin adverse events are also taken from various published studies.(16–21) For laboratory-based screening, the costs are split between the cost of the physician visit and the cost of the lipid panel test. For medication, we attempt to match costs with the medications used as intervention inputs.

Acute MI

The annual cost of acute MI is calculated by finding the weighted average between the 12-month cost of non-fatal MI and the cost of fatal MI.(22) The case-fatality of MI is used as the weight, and it is estimated from the raw average between the case-fatality of acute MI in ages below 65 (10%) and the case-fatality of acute MI in ages above 65 (16%).(16) The following equation is used to calculate the annual cost of acute MI:

$$C(\mathit{acute}MI)=C(\mathit{nonfatal}MI)\ast (1-F_{MI})+C(\mathit{fatal}MI)\ast F_{MI}$$

Acute Cardiac Arrest

Similarly, the cost of acute cardiac arrest is estimated as the weighted average between the cost of cardiac arrest at 12 months and fatal cardiac arrest.(22) We use the average case-fatality of acute cardiac arrest as the weight.(10) The annual cost of acute cardiac arrest is calculated using the following equation:

$$C(\mathit{acute}\mathit{cardiac}\mathit{arrest})=C(\mathit{nonfatal}\mathit{cardiac}\mathit{arrest})\ast (1-F_{\mathit{cardiac}\mathit{arrest}})+C(\mathit{fatal}\mathit{cardiac}\mathit{arrest})\ast F_{\mathit{cardiac}\mathit{arrest}}$$

Acute Stroke

The annual cost of acute stroke is calculated using the same method. We use the probability of acute death from stroke as our case-fatality weight.

$$C(\mathit{acute}\mathit{stroke})=C(\mathit{nonfatal}\mathit{stroke})\ast (1-F_{\mathit{stroke}})+C(\mathit{fatal}\mathit{stroke})\ast F_{\mathit{stroke}}$$

Table A-2 contains all cost values used in the model.

Treatment

Intervention inputs

The intervention inputs used in the model are screening interval and compliance, medication initiation and compliance, the relative risk reduction of medications, and the probability of a statin adverse event. The inputs were derived entirely from published literature, especially clinical trials, but also including meta-analyses and systematic reviews. In meta-analyses, if there were multiple studies informing a single input, we only considered those from the U.S., and took a weighted average of those values. If U.S. data was not available, we tried matching the input to that of data from other high income countries.

For primary prevention, we use cholesterol screening data and assumed that patients were also screened for hypertension at this time. Since the recommended interval for cholesterol screening is not explicitly reported by the American Heart Association, we use data from a systematic review of cardiovascular risk assessment guidelines.(23) This review states that the most frequently reported screening interval for total cardiovascular risk is five years.

The screening compliance rates come from a study that analyzed the National Ambulatory Medical Care Survey (NAMCS) data.(24) The study reports screening rates for different preventative services provided at physician offices to patients, which we consider to be the same as screening compliance. Since the study reports cholesterol screening rates for both patients at risk of CVD and patients without risk, we calculate the weighted average for use in our model.

Once screened, we use the Pooled Cohort Equations from the 2013 ACC-AHA cholesterol treatment guidelines to identify individuals eligible for statin therapy (10-year ASCVD risk >7.5%, in addition to patients with existing CVD, individuals with history of diabetes, and those with LDL >190 mg/dL).(25) For the validation analysis, we modeled the ATP-III screening guidelines and compliance rates that were in place during most of the time period that our validation cohort lived (1999–2011).(26, 27) These individuals are also eligible for aspirin therapy. Screened individuals with systolic blood pressure over 140 mmHg are also eligible for anti-hypertensive treatment.

For primary prevention using blood pressure treatment, we aggregate data for the following drugs: ACE Inhibitors, Angiotensin Receptor Blockers, Calcium Channel Blockers, Thiazides, and Beta Blockers. Compliance rates were calculated using studies from a meta-analysis on the adherence to cardiovascular disease medications.(28) We extracted only the U.S.-based studies to estimate the compliance rates for our validation. We derived initiation rates for each specific medication from published literature. The relative CVD risk reduction values for each medication came from various meta-analyses and systematic reviews.(29–32) We distinguished between primary and secondary prevention in our review of the literature and found unique model input values for each prevention type.

Table A-3 contains information on screening frequency, medication initiation and compliance, and statin adverse events. Table A-4 contains risk reductions used for each intervention.

Medication Initiation, Compliance, and Adverse Events

a. Statin initiation and compliance (primary and secondary prevention)

The initiation rate of statins for primary prevention came from a study on trends in statin use.(33) The initiation rate of statins for secondary prevention came from a study that examined the post-discharge use of secondary prevention medication among patients with Acute Coronary Syndrome.(34) Here, we use the utilization rate of statins at 12 months post-discharge of the patient.

Statin compliance during primary prevention is estimated using the Greving JP, et al, study.(35, 36) The study presents a trial-based compliance rate and a real-world compliance rate for the first, second, and third year. We divide the real-world compliance by the trial-based compliance for each year because the relative risk from statin trials includes non-compliance:

$$\mathit{Statin}\mathit{compliance}\mathit{rate}=\frac{\mathit{real}\mathit{world}\mathit{compliance}\mathit{rate}}{\mathit{trial}\mathit{based}\mathit{compliance}\mathit{rate}}$$

The first year compliance rate for statins during secondary prevention was estimated using the weighted average between compliance rates from two U.S.-based studies.(37, 38) These two studies were chosen from a meta-analysis of medication adherence on CVD-preventive drugs.(28) The second and third year compliance rate was estimated by applying the ratio between first, second, and third year statin compliance rates during primary prevention.(35) This procedure of applying primary prevention compliance rates in the second and third years to secondary prevention compliance rates was repeated for other medications in our model.

Statin-induced mild (myalgia or myopathy) and major (rhabdomyolysis) adverse event rates (4.7% and 0.006%, respectively) are based on a large retrospective cohort study of statin discontinuation.(39) Statins have been found to cause a small but significant increased risk of incident type II diabetes (odds ratio of 1.09).(40) Since the short-term effect of statin-induced diabetes on cardiovascular disease is already reflected in the hazard ratios for statins on cardiovascular disease events, we only included the quality-of-life (utility decrement of −0.20) and cost implications (additional annual costs of $4445) of statin-induced diabetes in our simulation model.(14, 41) Individuals with statin-induced diabetes in the Disease Free state would also be at higher long-term risk for cardiovascular disease since presence of diabetes contributes to the underlying coronary heart disease and stroke risk equations used in the model.(7, 42)

b. Blood pressure treatment (primary prevention)

We assume that the initiation rate of blood pressure treatment in the primary prevention level would be equal to the initiation rate in the secondary prevention. The seventh report of the Joint National Committee (JNC) on prevention, detection, evaluation, and treatment of high blood pressure reported that 59% of patients with hypertension receive treatment. We use this value as the initiation rate of blood pressure treatment.(43)

The compliance rate of blood pressure treatment for primary prevention is estimated by aggregating the compliance rates of ACE Inhibitor, Angiotensin Receptor Blocker, Calcium Channel Blocker, Thiazides, and Beta Blocker. We selected only the U.S.-based studies from a meta-analysis of CVD preventive medication adherence, and then we calculate the weighted average of the blood pressure treatment compliance rates from the selected studies.(28, 44, 45)

c. Aspirin initiation and compliance (primary and secondary prevention)

The initiation rate of aspirin for primary prevention comes from a study which analyzed the National Ambulatory Medical Care Survey (NAMCS) and determined the probability that aspirin will be prescribed to patients with CVD risk factors for preventive purposes.(24) The initiation rate of aspirin in the secondary prevention stage is based on a trial data from Utah.(46) The study introduced an intervention that improves the appropriate medication prescription before patients being discharged. We use the percentage of patients that were prescribed aspirin in the control group for the initiation rate of aspirin.

We could not find any studies on the compliance rate of aspirin use during primary prevention. Thus, we use the studies presented in a meta-analysis of CVD preventive drug adherence, and assumed that the compliance rate for aspirin is equal to the overall compliance rate of CVD treatment for primary prevention. We justify this assumption from a statement in the study stating that drug class is not a big factor in determining adherence to medication.(28) The compliance rate of aspirin for secondary prevention is presented in the meta-analysis, but the data was not from U.S.-based studies.(28) Although studies with a non-U.S. setting (e.g. Italy, Netherland, Australia, and Canada) are included, we assume that the U.S. would have the same compliance rates as the global estimates.

d. ACE Inhibitor initiation and compliance (secondary prevention)

The initiation rate of ACE Inhibitors are from a study that analyzed the usage of secondary prevention CVD drug treatment in patients with acute coronary syndrome after being discharged from the hospital.(34) If patients had at least one pharmacy claim for the medication from the index date to three months post-index date, the drug was considered to be utilized by that patient. We use the utilization rate at 12 months post-discharge as the initiation rate. This number is approximately the same as the prescription rate of ACE Inhibitors to CVD patients being discharged in a Utah-based study.(46)

The compliance rates of ACE inhibitors are from a U.S.-based study which was included in a meta-analysis of adherence to CVD preventive medications.(28, 38) This is used as the first year compliance rate. The second and third year compliance rates are calculated by applying the first, second, and third year statin compliance ratio.(35)

e. Beta Blocker initiation and compliance (secondary prevention)

The initiation rate of beta-blockers are from the same study we used for the ACE Inhibitor initiation rate.(34) Likewise, we use the 12-month post-discharge utilization rate of the beta-blocker.

The beta-blocker first year compliance rate is estimated by calculating the weighted average of the compliance rates from two U.S.-based studies.(28, 38, 47) The second and third year compliance rate is calculated by applying the first, second, and third year statin compliance rate ratio.(35)

Probabilistic Sensitivity Analysis

Overall model uncertainty is assessed in a probabilistic sensitivity analysis (PSA), where 1,000 random values for key model parameters are drawn from pre-specified probability distributions. In a given PSA iteration, the model fixes the values of each input parameter based on the draws and runs the micro-simulation for the 1,000,000 individuals in the model.(48) The process is repeated for 1,000 PSA iterations to generate 1,000 sets of model input draws and cost-effectiveness results that can be used to generated cost-effectiveness acceptability curves.(49) Distributions are assigned based on data characteristics and ability to account for distribution skewness (gamma distributions for costs, beta distributions for utilities, lognormal distributions for odds ratios, and so on); we focus our PSA on variables that have the most impact on cost-effectiveness analyses, such as treatment benefits and risks.(50)

We did not include a PSA for our model validation exercise; instead, we focused the validation analysis on comparing the point estimates of the model-based survival curve to the bootstrapped confidence intervals of the observed survival data to simplify the visual presentation of the survival curves. Additionally, there is no standard method for comparing the confidence/credible intervals of two survival curves in disease model validation analyses; this could be an area for future research. Certainly, the PSA feature of model is essential when comparing strategies in comparative- and cost-effectiveness studies.

Table A-1.

Utilities used in the CVD PREDICT model

Parameter	Base-case Value	Base-Case Source
Disease Free	0.877	Sullivan 2006 (15), Mozafarrian 2016 (3)
Chronic Cardiac Arrest	0.808	Sullivan 2006 (14), Taylor 2009 (15)
Chronic MI	0.778	Sullivan 2006 (14)
Chronic MI with CABG	0.778	Sullivan 2006 (14)
Chronic Angina	0.768	Sullivan 2006 (14)
Chronic Angina with CABG	0.768	Sullivan 2006 (14)
Chronic Stroke	0.768	Sullivan 2006 (14)
Utilities for Acute Disease States (disabilities for acute state in parentheses)
Acute Cardiac Arrest	0.770 (−0.0409)	Sullivan 2006 (14)
Acute MI	0.737 (−0.0409)	Sullivan 2006 (14)
Acute MI with CABG	0.737 (−0.0409)	Sullivan 2006 (14)
Acute Angina	0.727 (−0.0412)	Sullivan 2006 (14)
Acute Angina with CABG	0.727 (−0.0412)	Sullivan 2006 (14)
Acute Stroke	0.716 (−0.0524)	Sullivan 2006 (14)
Disutilities for Events
Repeat MI	−0.041	Sullivan 2006 (14)
Repeat Stroke	−0.052	Sullivan 2006 (14)
CABG	0	assumption
PTCA	0	assumption
Statin	−0.002	Gage 1996 (51), Hutchins 2015 (52)
Minor statin adverse event	−0.005	Lee 2010 (16) (2 days of life lost)
Major statin adverse event	−0.038	Lee 2010 (16) (2 weeks of life lost)

Table A-2.

Costs (2013 US dollars) used in the CVD PREDICT model

Parameter	Base-case Value	Base-Case Source
Costs for Chronic Disease States
Disease Free	$0	Assumption: None
Chronic CHD	$3,201	Lee 2010 (16)
Chronic Stroke	$2,115	Pignone 2006 (17)
Costs for Acute Disease States
Acute Cardiac Arrest	$19,271	O’Sullivan 2011 (22)
Acute MI	$56,358	O’Sullivan 2011 (22)
Acute Angina	$29,139	O’Sullivan 2011 (22)
Acute Stroke	$19,128	O’Sullivan 2011 (22)
Costs for Procedures and Repeat Events
Repeat MI	$56,358	O’Sullivan 2011 (22)
Repeat Stroke	$19,128	O’Sullivan 2011 (22)
CABG	$36,872	O’Sullivan 2011 (22)
PTCA	$34,742	O’Sullivan 2011 (22)
Screening Costs
Non-lab test (GP visit in Stage 1)	$75	Pletcher 2009 (19)
Cholesterol (lab) test	$35	Pletcher 2009 (19)
# extra GP visits during Stage 2	1	Assumption
# lab tests/year after treatment	1	Lazar 2011 (53), Expert Opinion
# GP visits/year after treatment	1	Lazar 2011 (53), Expert Opinion
Statin Drug and Adverse Event Costs
Statin	$267	Redbook 2009 (54)
Anti-hypertensive	$206	Nuckols 2011 (20)
Aspirin	$7.6	Pignone 2006 (17)
ACE Inhibitor	$52.12	Shah 2011 (21), Redbook 2009 (54)
Beta Blocker	$52.12	Shah 2011 (21), Redbook 2009 (54)
Mild adverse event	$178.53	Lee 2010 (16)
Major adverse event	$7,033	Lee 2010 (16)

Table A-3.

Intervention inputs used in the CVD PREDICT model

Parameter	Base case value	Base Case Source
Screening
Screening interval	5	Ferket 2010 (23)
Initiation
Medication initiation	0.87	Arnold 2014 (55)
Aspirin (primary prevention)	0.435	Applied 2:1 ratio to medication initiation
Compliance (primary prevention)
Statin
Compliance Year 1	0.667	Greving 2011 (35), Avorn 1998 (36)
Compliance Year 2	0.53	Greving 2011 (35), Avorn 1998 (36)
Compliance Year 3	0.5	Greving 2011 (35), Avorn 1998 (36)
Blood Pressure Treatment
Compliance Year 1	0.539	Naderi 2012 (28), Elliott 2007 (45), Bloom 1998 (44)
Compliance Year 2	0.428	Applied statin compliance ratio year 1: year 2: year 3
Compliance Year 3	0.404	Applied statin compliance ratio year 1: year 2: year 3
Aspirin
Compliance Year 1	0.5	Naderi 2012 (28)
Compliance Year 2	0.397	Applied statin compliance ratio year 1: year 2: year 3
Compliance Year 3	0.375	Applied statin compliance ratio year 1: year 2: year 3
Initiation & compliance (secondary prevention)
Statin
Compliance Year 1	0.729	Naderi 2012 (28), Kopjar 2003 (37), Ho 2008 (38)
Compliance Year 2	0.579	Applied statin compliance ratio year 1: year 2: year 3
Compliance Year 3	0.546	Applied statin compliance ratio year 1: year 2: year 3
Aspirin
Compliance Year 1	0.65	Naderi 2012 (28)
Compliance Year 2	0.516	Applied statin compliance ratio year 1: year 2: year 3
Compliance Year 3	0.487	Applied statin compliance ratio year 1: year 2: year 3
ACE Inhibitor
Compliance Year 1	0.78	Ho 2008 (38)
Compliance Year 2	0.62	Applied statin compliance ratio year 1: year 2: year 3
Compliance Year 3	0.585	Applied statin compliance ratio year 1: year 2: year 3
Beta Blocker
Compliance Year 1	0.557	Naderi 2012 (28), Ho 2008 (38), Kramer 2006 (47)
Compliance Year 2	0.443	Applied statin compliance ratio year 1: year 2: year 3
Compliance Year 3	0.418	Applied statin compliance ratio year 1: year 2: year 3
Statin Adverse Events
Minor Events	0.047	Zhang 2013 (39)
Major Events	0.00006	Zhang 2013 (39)
Major Death Events	0.09	Lee 2010 (16)

Table A-4.

Risk adjustment based on Treatment (Relative Risk Reduction)

Parameter	Base Case Value	Sensitivity Analysis Value	Source
Relative Risk in the Primary Prevention
Statin
CHD	0.75	0.71–0.78	Baigent 2005 (30)
Stroke	0.83	0.76–0.87	Baigent 2005 (30)
Aspirin
CHD	0.82	0.75–0.9	ATT Collaboration 2009 (56)
Stroke	0.95	0.85–1.06	ATT Collaboration 2009 (56)
Blood Pressure Treatment
CHD	0.84	0.79–0.9	Law 2009 (57)
Stroke	0.64	0.56–0.73	Law 2009 (57)
Relative Risk in the Secondary Prevention
Statin
Death	0.88	0.84–0.92	Cholesterol Treatment Trialists 2012 (31)
MI	0.76	0.73–0.79	Cholesterol Treatment Trialists 2012 (31)
Stroke	0.85	0.81–0.9	Cholesterol Treatment Trialists 2012 (31)
Aspirin
Death	0.91	0.82–1.00	ATT Collaboration 2009 (56)
MI	0.69	0.6–0.8	ATT Collaboration 2009 (56)
Stroke	0.81	0.71–0.92	ATT Collaboration 2009 (56)
ACE Inhibitor
Death	0.87	0.81–0.94	Baker 2009 (29)
MI	0.83	0.73–0.94	Baker 2009 (29)
Stroke	0.78	0.63–0.97	Baker 2009 (29)
Beta Blocker
Death	0.94	0.79–1.10	Lindholm 2005 (32)
MI	0.89	0.74–1.06	Lindholm 2005 (32)
Stroke	0.84	0.64–1.10	Lindholm 2005 (32)

Figure A-1.

Survival curves restricted to individuals with imputed data.

Figure A-2.

ROC curves restricted to individuals with imputed data.

Figure A-3.

Predicted versus observed mortality by CVD PREDICT model-based risk quintile.