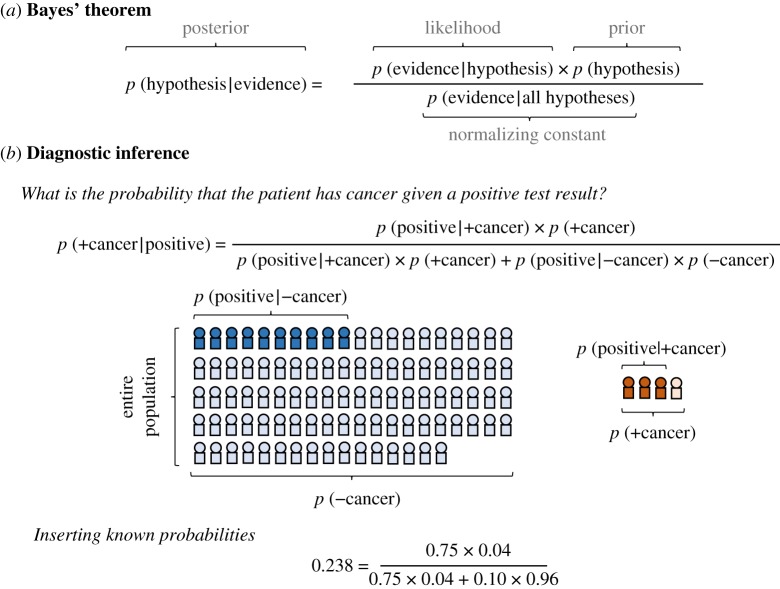
Figure 6.

Bayesian inference. (a) Bayes' theorem. Here, ‘p’ means probability and ‘|’ means given, so p(hypothesis|evidence) means probability that the hypothesis is true given the evidence. The normalizing constant, which is not discussed in the appendix, is the marginal likelihood of observing the data irrespective of the hypothesis and ensures that the posterior probabilities for the different hypotheses add up to 1. (b) Using Bayes' theorem in diagnostic inference. A doctor wishing to compute the probability that a patient has prostate cancer given a positive test result, p(+cancer|positive). We know that the test makes correct detections in 75% of cases, p(positive|+cancer) = 0.75, and gives false positives in 10% of cases, p(positive|−cancer) = 0.10. We also know that the base-rate of prostate cancer is only 4%, p(+cancer) = 0.04.