FIG. 2.

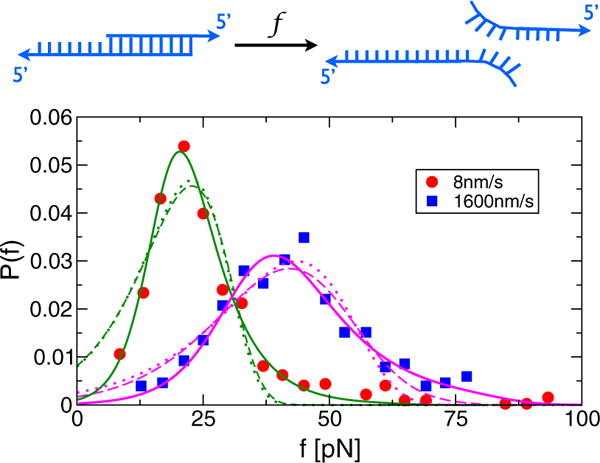
(color online). Analysis of rupture force distributions from a DNA unzipping force spectroscopy experiment (the AFM cantilever spring constant ≈2 pN/nm) [17] using three different models. The fits using $P_{\lambda }^{\gamma }(f)$ (solid lines), based on our FB model, yield (Δx^‡[nm], k₀θ[s⁻¹],λ[s⁻¹]) = (1.1;0.017;2.8×10⁻⁵) for v = 8 nm/s and (0.66, 0.99, 0.48) for v = 1600 nm/s. The fits using P_cubic [ε(f)] = (k(ε)/γ) exp [(k₀/γΔ x^‡) × (1 − (k(ε)/k₀)ε⁻¹⁼²)] (dashed lines) with $k(\epsilon )=k_0{\epsilon }^{1/2}{e}^{\mathrm{\Delta }{G}^{‡(1-{\epsilon }^{3/2})}}$ and ε(f) = 1–2f Δx^‡/3ΔG^‡ [23] yield (Δ x^‡[nm]; k₀[s⁻¹]; ΔG^‡[pN·nm]) = (0.12;0.12;31.9) for v = 8 nm/s and (0.09,7.16,19.0) for v = 1600 nm/s. The fits using $P_{\text{Bell}}(f)={\gamma }^{-1}{k}_0{e}^{f\mathrm{\Delta }{x}^{‡}/k_{B}T}\times \exp (-{\gamma }^{-1}{k}_0{k}_{B}T/\mathrm{\Delta }{x}^{‡}\times (e^{f\mathrm{\Delta }{x}^{‡}/k_{B}T}-1))$ (dotted lines) yield (Δx^‡ [nm]; k₀[s⁻¹]) = (0.49; 0.13) for v = 8 nm=s and (0.32, 8.19) for v = 1600 nm=s. Note that P_λ(f) describes the heavy tails of the distributions better than P_cubic(f) or P_Bell(f), implying that unbinding of these DNA duplexes by force cannot be accounted for using one-dimensional models.